Python 练习题 --- 梯度下降

• 题目来源：在校课程老师布置的作业
• 偷偷说一句：如果对我的答案和解析满意的话可不可以给我 点个赞 ， 点个收藏 之类的
• Let's do it !!!

题目要求

已知某系统模型可由 $y=2x+3$ 表示

对该系统实际采样得到 4 个样本：(0，3.1)、(1，4.9)、(2，7.2)、(3，8.9)

根据采样数据使用一维线性回归算法估计该模型：$f(x)=wx+b$

选取损失函数：$L=\frac{1}{2n}\sum _{i=1}^n{(y^i-(b+w{x}^i))}^2$

基于 梯度下降算法 估计参数 w 和 b。

提示：
$gra{d}_w=\frac{\partial L}{\partial w}=\frac{1}{n}\sum _{i=1}^n(f\left(x^i\right)-y^i)x^i$

$gra{d}_b=\frac{\partial L}{\partial b}=\frac{1}{n}\sum _{i=1}^n(f\left(x^i\right)-y^i)$

其中：

• n 是样本数，（$x_i$，$y_i$）是样本点，$f(x_i)=b+w{x}^i$ 是模型估计值。

问题：

1. 假设初始值 w = 0，b = 0，学习率 η= 0.01，根据已采集的 4 个样本，基于 梯度下降算法 估计 w 和 b，请计算 第1次 至 第3次 迭代的结果，要求 给出计算过程 及 每次迭代后的平均误差 。

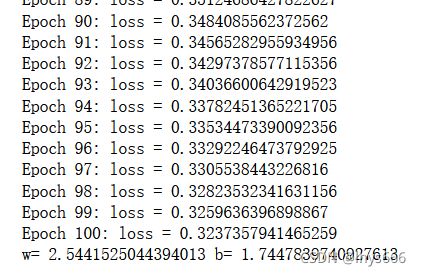
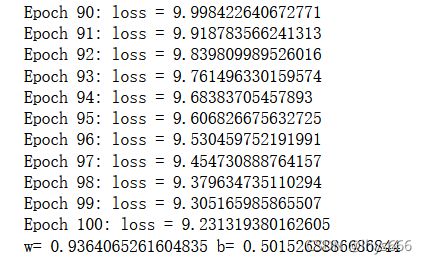
• 假设初始值 w = 0，b = 0，请用 python 编程计算学习率为 η= 0.01 和 η= 0.001 时迭代 100 次的结果。

思路讲解

这道题就是简单的 梯度下降 ，公式已经给出来了，我们就直接按照公式实现即可。

第一题

第一题要求手写，有了初始条件 $w=0,b=0,\eta =0.01$ ，很容易写出来梯度下降的过程。
我写了个程序输出，代码如下：

w = 0
b = 0
eta = 0.01

def process():
    
    global w, b
    
    x = x_train.reshape(1, -1)[0]
    y_hat = x * w + b
    y = y_train.reshape(1, -1)[0]
    diff = y - y_hat
    
    print('(' + '+'.join(map(lambda x:str(round(x, 4)), diff**2)) + f')/{
       2*x.shape[0]} =', round((diff**2 / (2*x.shape[0])).sum(), 4))
    
    grad_w = -diff * x
    print('(' + '+'.join(map(lambda x:f'({
       round(x, 4)})', grad_w)) + f')/{
       x.shape[0]} =', round(grad_w.sum() / x.shape[0], 4))
    w -= eta * grad_w.sum() / x.shape[0]
    print('w =', w)
    grad_b = -diff
    print('(' + '+'.join(map(lambda x:f'({
       round(x, 4)})', grad_b)) + f')/{
       x.shape[0]} =', round(grad_b.sum() / x.shape[0], 4))
    b -= eta * grad_b.sum() / x.shape[0]
    print('b =', b)

for i in range(1, 4):
    print('Epoch', i)
    process()
    print()

• Epoch 1 ：
  $$\begin{gathered} loss=(9.61+24.01+51.84+79.21)/8=20.5838 \\ gra{d}_w=((-0.0)+(-4.9)+(-14.4)+(-26.7))/4=-11.5 \\ w=0.115 \\ gra{d}_b=((-3.1)+(-4.9)+(-7.2)+(-8.9))/4=-6.025 \\ b=0.06025 \end{gathered}$$
• Epoch 2 ：
  $$\begin{gathered} loss=(9.2401+22.3233+47.7446+72.1608)/8=18.9336 \\ gra{d}_w=((-0.0)+(-4.7248)+(-13.8195)+(-25.4842))/4=-11.0071 \\ w=0.2251 \\ gra{d}_b=((-3.0398)+(-4.7248)+(-6.9098)+(-8.4948))/4=-5.7922 \\ b=0.1182 \end{gathered}$$
• Epoch 3 ：
  $$\begin{gathered} loss=(8.8913+20.764+43.9792+65.7172)/8=17.419 \\ gra{d}_w=((-0.0)+(-4.5568)+(-13.2634)+(-24.3198))/4=-10.535 \\ w=0.3304 \\ gra{d}_b=((-2.9818)+(-4.5568)+(-6.6317)+(-8.1066))/4=-5.5692 \\ b=0.1739 \end{gathered}$$

第二题

要计算 η= 0.01 和 η= 0.001 时的结果，我们可以把能复用的地方封装成函数，以简化我们的代码。

第一步

首先要 初始化数据：

w = 0
b = 0
X = [0., 1., 2., 3.]
Y = [3.1, 4.9, 7.2, 8.9]

• 学习率我们可以作为参数传递给函数

第二步

计算 $\hat{y}$。

def forward(w, X, b):
	result = []
	for x in X:
		result.append(w*x+b)
	return result

第三步

计算 损失 loss 。

def get_loss(X, Y, Y_PRED):
	result = []
	for i, y in enumerate(Y):
		result.append((y - Y_PRED[i])**2)
	return sum(result) / len(X)

第四步

迭代 计算损失 ，并 更新 w 和 b ，传入参数 学习率 η。

• 将初始化数据加入函数中，这样每次更改学习率进行训练就不需要再初始化数据。

def train(eta):
    
    w = 0
    b = 0
    x_train = [0., 1., 2., 3.]
    y_train = [3.1, 4.9, 7.2, 8.9]
    
    for step in range(1, 101):
        y_pred = forward(w, x_train, b)
        loss = get_loss(x_train, y_train, y_pred)
        print('Epoch {}: loss = {}'.format(step, loss))
        
        w -= -eta * sum([x * (y - y_hat) for x, y, y_hat in zip(x_train, y_train, y_pred)]) / len(x_train)
        b -= -eta * sum([y - y_hat for y, y_hat in zip(y_train, y_pred)]) / len(x_train)

第五步

传参 。

• η= 0.01 ：
  
• η= 0.001 ：
  

改进

• 使用 numpy 数组进行计算操作会更简便。
• 封装成类 会更好看。
• （当然，我的作业包括以上两点）

---

---

---

结尾

有想要一起学习 python 的小伙伴可以扫码进群哦。

以上就是我要分享的内容，因为学识尚浅，会有不足，还请各位大佬指正。
有什么问题也可在评论区留言。