数据分析项目——学生在线学习成绩预测模型构建全过程

背景：这是我在去年疫情期间做的数据分析项目，在项目结束之后，我将整个流程整理成了一份教学文档，供后续有类似需求的时候使用，其实不管是做「数学建模」还是「数据分析」都一定的参考价值，话不多说，从安装环境开始吧。

运行环境的安装教程

如果一个有关于数据分析的教学项目想要介绍Python的打开方式不是从安装Anaconda和使用Jupyter Notebook开始，那么对于初学者就意味着落入无限崩溃的深渊，Python本身的命令窗口模式不支持可视化，学习和练习起来上手难度较大，各种IDE解释器也是各有优劣。

Anaconda自带的各种第三方工具能够免去后续学习中的麻烦，直接导入非常方便，Jupyter Notebook的使用更是精简轻便，可视化效果好，有利于理解语句和理清思维。本部分以Windows环境下Anaconda的安装为例来进行演示，具体如下：

（1）打开浏览器，在地址栏输入“https://www.anaconda.com/”，进入 Anaconda 官网，
单击右上角 “Get Start”导航栏进行跳转，随后点击最下方的“Download Anaconda installers”进一步跳转。

（2) 进入下载页面，根据当前计算机操作系统的版本选择并下载相应版本的 Anaconda 安装程序，这里以 Windows 下基于 Python 3.8 的 64 位安装程序为例。

（3）由于我的电脑是Mac，安装器和Windows的有所不同，下面我用讲义里的内容带大家安装。将下载好的 .exe ⽂件打开，进⼊安装程序，以下图的顺序依次安装。


（4) 选择软件使用者的权限，选择推荐的“Just Me”即可，随后将Anaconda安装到你指定的⽬录，为了避免不必要的麻烦，建议按默认即可，需要占用空间大约 2.6 G左右。


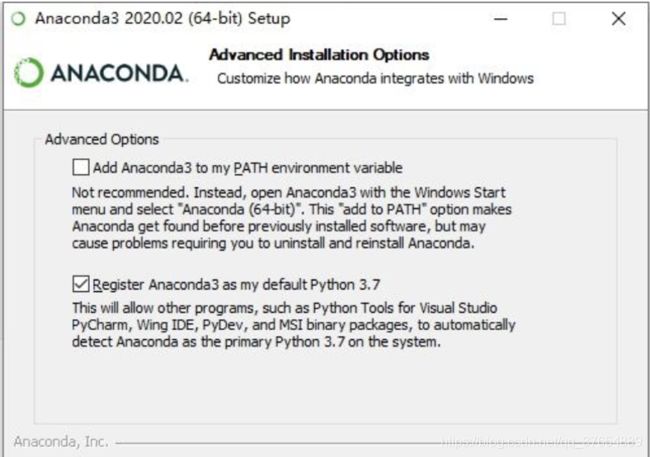
（5) 接着，勾选第一项表示将 Anaconda 及相关组件的启动文件路径加入系统环境变量，方便后续安装 Anaconda 扩展软件；勾选第二项表示将 Anaconda 自带的 Python 3.7 注册为系统默认的 Python 环境，当然我们用的是3.8，若计算机未安装任何 Python 环境，这里建议把两个都勾上，可以免去后续配置环境变量的麻烦，随后安装需要耗费⼀定时间，请耐⼼等待。


（6) 安装完成后会显示如下界⾯，分别点击“next”和“Finish”即可，为了避免跳出相关⽹ ⻚，注意去掉后⾯的两个勾选项。


（7) Windows环境下，利用cmd打开命令行（最好用管理员模式打开）输入conda –V命令，查看Anaconda的版本号，这里我是Mac环境下的验证，如果看到了版本号则代表安装成功，如下：

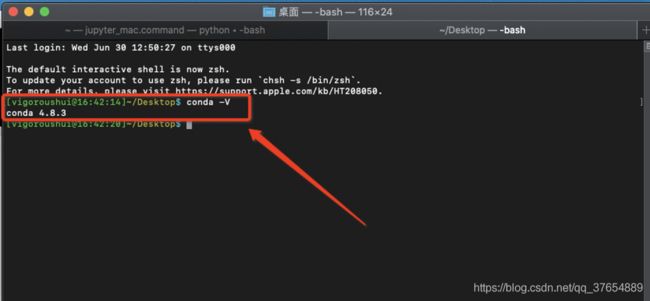
以上便完成了Anaconda的安装过程，⾄于Jupyter Notebook的打开⽅式为：进⼊Anaconda后点击 Jupyter Notebook即可启动。Jupyter Notebook以⽹⻚的形式打开，可以在⽹⻚⻚⾯中直接编写代码和 运⾏代码，代码的运⾏结果也会直接在代码块下显示的程序。

学生在线学习成绩预测

本项目主要使用 Python 中的程序库 Numpy、Pandas和sklearn(Scikit-learn)做学生在线学习成绩预测模型以及程序库 Matplotlib 实现数据的可视化（Anaconda环境中已集成）。正是因为有了Scikit-Learn，我们才不需要具体实现所有的机器学习算法，只需要调用包中的函数(接口)即可。同时这四个库也是常规机器学习的四大利器。

• Numpy: 提供了高效存储和操作密集数据缓存的接口。
• Pandas: 提供了一种高效的DataFrame数据结构，DataFrame本质上是一种带有行标签和列标签、支持相同类型数据和缺失值的多维数组。
• Scikit-learn: 用于机器学习的模块，包括数据的预处处理、特征工程、模型训练、超参数调优、模型测试和模型评估。
• Matplotlib: 基于Numpy库的数据可视化利器，集成了多种图形的接口。
  ​ 简单来说，Numpy、Pandas是用于做数据载入、处理和查看的工具，Scikit-learn是用于模型构建的工具，Matplotlib是将结果可视化的工具。

项目的总目标：通过某校在线学习平台的数据来探究学生在线学习行为对最终成绩的影响。

1 数据预处理

学生在线学习行为最原始数据应该是什么样子的？ ==> “点击行为的埋点⽇志”。

例如，某学⽣观看⼀次视频课程，数据的部分呈现形式是“2020-10-28 08:00:00”到 “2020-10-28 08:42:33” ，我们通过计算可以得知该学⽣看视频的时⻓为42分33秒，看视频的次数+1。

显然，这两个特征(视频时⻓、视频次数)都是经过对埋点⽇志统计得出的，这也是特征⼯程中数据特征的⽣成过程。

注意：对于不同的埋点⽇志有着不同的处理⽅法，整个过程⼗分繁琐，为了重点讲解建模的过程，我们选⽤的数据是经过⽣成后的统计数据。

1.1 数据概览

本项目采用已脱敏(用id来代表每个学生)的原始数据，其格式为xlsx，样本数据量为310170*51​。由于脱敏处理导致无法查看学生的真实学号(无法统计学生的真实人数)，所以本项目将​个样本数据假设为​310170名学生产生的数据。此外，直接利用Pandas库中的read_excel()函数来进行数据的读取和head()函数查看数据，代码如下：

import pandas as pd
path = 'statistics_student_clazz.xlsx' # 设置原始数据的路径
data = pd.read_excel(path) # 读取excel文件数据
data.head(5) # 显示数据的前5行, 打印的格式：print(data.head(5))

打印结果如下：

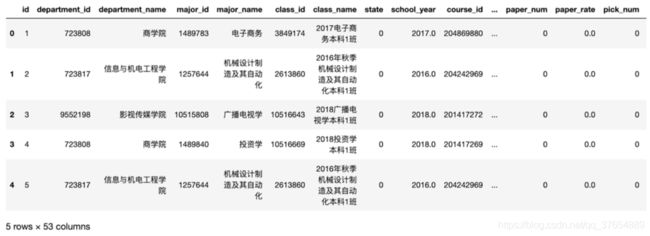
利用data.columns可获取该数据集的各字段名称，其对应的解释如下表所示：

字段(特征)	解释	字段(特征)	解释	字段(特征)	解释
id	学生编号	department_id	学院编号	department_name	学院名称
major_id	专业编号	major_name	专业名称	class_id	班级编号
class_name	班级名称	state	记录变化	school_year	入学年份
course_id	课程编号	course_name	课程名称	jwcourse_id	教务课程编号
create_time	创建时间	course_type	课程类型	clazz_id	教学班编号
course_delete	已删除课程	course_status	课程状态	clazz_name	教学班名称
clazz_status	教学班状态	job_num	任务点数	clazz_state	教学班变化
job_rate	任务点完成率	videojob_num	视频数	videojob_rate	视频完成率
videojob_time	视频完成时长	test_num	章节测试数	test_rate	章节测试完成率
test_avgscore	章节测试平均分	work_num	作业数	work_rate	作业完成率
work_avgscore	作业平均分	exam_num	考试数	exam_rate	考试完成率
exam_avgscore	考试平均分	sign_num	签到数	sign_rate	签到率
course_live_time	在线课程时长	special_time	特殊时间	bbs_num	讨论数
topic_num	发帖数	reply_num	回帖数	points	点数
paper_num	问卷数	paper_rate	发问卷率	pick_num	抢答数
answer_num	答题数	markscore_num	记分数	markscore_rate	记分率
pv	访问量	task_num	任务数	task_rate	任务完成率
update_time	更新时间	insert_time	插入时间

1.2 数据处理

为了对数据有更好的把控感，我们需要对数据进行处理，整个过程分为两步走：一是查看相关数据；二是根据各字段实际含义删除异常值。具体为：

（1）根据insert_time字段查看原始数据产生的时间跨度。代码如下：

data.insert_time.sort_values() # 对插入时间进行从小到大排序
# Out: 数据产生的时间区间为'2016-02-26 13:55:56'到'2020-08-19 23:07:48'

（2）模型构建的目的是根据学生学习行为预测学生的学习成绩，那么很自然地需要删除没有期末成绩的学生样本，根据exam_avgscore字段滤除成绩为0以及空值的样本。代码如下：

data['exam_avgscore'].isna().sum() # Out: 0 没有空值
data = data[data['exam_avgscore']!=0].reset_index(drop=True)
# Out: 学生学习行为记录数变化情况: 310170 => 56765

（3）根据department_name字段查看原始数据中各个学院的人数，由于某校只有18个学院（除继续教育学院），故在原始数据中删除学院不符合要求的样本，具体的处理思想：首先定义符合要求的学院，接着删除每一个学院名称中的多余空格（如 ‘ 信息与机电 工程 学院 ’ => ‘信息与机电工程学院’），借助自定义的label筛选出符合要求的样本。筛选后的样本数量为54788*53​，这意味着有​1977(56765-54788)条数据不符合要求，在数据处理的过程中称它们为脏数据。代码如下：

data.department_name.value_counts() # 用于各学院人数的统计,存在70个学院信息，这是后台数据库的问题 
# 删除学院不符合要求的样本
department_columns = ['人文学院', '教育学院', '哲学与法政学院', '马克思主义学院', 
                      '外国语学院', '商学院', '对外汉语学院', '旅游学院', 
                      '音乐学院', '美术学院', '影视传媒学院', '体育学院', 
                      '数理学院', '生命科学学院', '化学与材料科学学院', 
                      '环境与地理科学学院', '信息与机电工程学院', 
                      '建筑工程学院'] 
data['department_name'] = data['department_name'].apply(lambda x: str(x).replace(' ', '')) 
data['label'] = data['department_name'].apply(lambda x: 1 if x in department_columns else 0)
data = data[data['label']==1].reset_index(drop=True).drop(columns='label') 

（4）从宏观上查看剩余数据是否还存在缺失值NaN，经统计发现，有5个字段存在缺失值分别为: major_name、class_name、jwcourse_id 、clazz_name、school_year，由于major_id已经可以唯一确定该学生的专业，所以该字段所在的列数据直接删除（class_name 、clazz_name同理），jwcourse_id中存在过多缺失值无法填充，故直接删除，school_year中只存在一个缺失值，查看该值所在样本的具体信息，根据脱敏前的数据，可以推测出该值为2019，代码如下：

data.isna().sum() 
# Out: major_name 15；class_name 16；jwcourse_id 52173；clazz_name 31379
data = data.drop(columns=['major_name', 'class_name', 'jwcourse_id', 'clazz_name']).reset_index(drop=True)
na = data.school_year.isna()[data.school_year.isna()==True] # 寻找缺失值所在行
data.school_year.fillna(2019, inplace=True)

此时的样本数据量变为​54788 * 49，本章仅对数据数据进行了简单的处理，数值指标异常值的判定、特征的选择和成绩标签的标注将在特征工程部分展开介绍。经过处理后的各学院学生行为记录数如下图所示，代码见附录(1)：

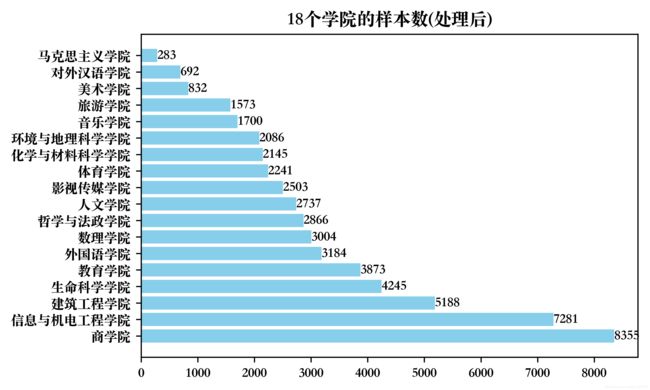
从上图可以观察各学院的学生对于在线学习的参与情况，但是各学院总人数未知，所以无法根据参与人数去推测学生的在线学习热情。仅从图中可以发现商学院、信息与机电工程学院的学生参与在线学习且产生学习成绩的人数显著多于其他学院。

最后，查看各学院的平时测验成绩平均分和期末成绩平均分是否有差异性。为避免没有平时测验成绩的学生拉低学院的平均分，需要暂时删除平时测验成绩为0分的记录数后进行对比分析。经过处理后的各学院学生的平均分情况如下图所示，代码见附录(2)：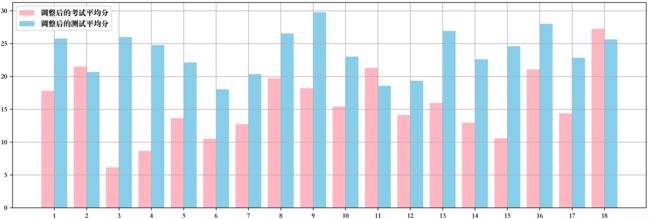
上图的x轴坐标分别代表18个学院的编号，分别为人文学院、体育学院、信息与机电工程学院、化学与材料科学学院、哲学与法政学院、商学院、外国语学院、对外汉语学院、建筑工程学院、影视传媒学院、教育学院、数理学院、旅游学院、环境与地理科学学院、生命科学学院、美术学院、音乐学院和马克思主义学院。其中调整后的分数是指该分是减去 60 分后的结果，从图中可以发现大多数学院学生的平时测试平均分显著高于期末考试平均分，只有体育学院、教育学院和马克思主义学院例外。

2 特征工程

特征工程是利用数据领域（教育）的相关知识来创建能够使机器学习算法达到最佳性能的特征的过程，本部分从「特征分析」和「特征选择」这两大视角来探索数据的特征。

2.1 特征分析

2.1.1 指标筛选

在探究各学习行为特征与最终成绩的相关性之前，先对各指标进行数值上的统计，虽然在数据预处理(章节1)中已经删除了带有的NaN值所在的列，但是经实验发现还存在数值大部分为0值的指标，这些指标对预测期末成绩毫无作用，我们以 “0值的数量不能超过总数据量的60%“ 的标准过滤不符合要求的指标，这个的过程称为指标筛选，代码如下：

columns = data.columns
zero_nums = [0 for i in range(len(columns))]
for i in range(len(columns)):
  zero_num = data[data[columns[i]] == 0].shape[0] # 统计每一列0值的数量
  zero_nums[i] += zero_num
zero_nums = pd.Series(zero_nums, index=columns) # 展示了每一列中存在的0值
columns_delete = list(zero_nums[zero_nums>len(data)*0.6].index) # 筛选出待删除的列名
data = data.drop(columns = columns_delete)
# Out: 指标数量变化情况: 49 => 23

筛选后的指标还剩余23个，其中有11个为数值类型指标、9个为类别类型指标、3个为时间类型指标，随后根据“指标代表含义是否重复”和“指标代表含义是否有意义”两个标准对指标进行进一步筛选，如下：

• 类别类型：由于department_id和department_name代表的含义相同，所以删除其中一个即可，coruse_id和course_name同理。id为学生的编号，无法体现学生的学习特性，故删除
• 时间类型：create_time和insert_time是系统统一创建和插入的，两个指标只能体现出在线学习平台更新数据的时间特性，无法体现出学生学习的特性，故删除。update_time是学生最后一次埋点日志信息产生时间，我们将其视作学生的学习特性，可用于后续的特征生成，故保留

columns_delete2 = ['id', 'department_id', 'course_name',
                   'create_time', 'insert_time']
data = data.drop(columns=columns_delete2)
# Out: 指标数量变化情况: 23 => 18

最终选取的指标分别「基本信息指标」、「学习行为指标」和「其他信息指标」，如下表所示：

基本信息指标		学习行为指标		其他信息指标
department_name	major_id	job_num	videojob_num	test_avgscore
class_id	school_year	videojob_time	test_num	exam_avgscore
course_id	clazz_id	pv	work_num	work_avgscore
		sign_num	exam_num	update_time

2.1.2 异常值的判定

本部分提供一种针对数值型指标是否存在异常值的判定方法，名为拉依达准则，但所有数值型指标的数据都是根据规则计算出的统计数据，数值型数据也不符合正态分布，所以即使发现了异常值，也不进行处理，代码如下：

• 拉依达准则：指先假设一组检测数据只含有随机误差，对其进行计算处理得到标准偏差，按一定概率确定一个区间，认为凡超过这个区间的误差，就不属于随机误差而是粗大误差，含有该误差的数据应予以剔除，但是监测数据需要符合正态分布或近似正态分布。

# 依据拉依达准则清除异常数据（本项目不使用）
def raida_criterion(data):
  import copy
  data_copy = copy.deepcopy(data)
  raida = []
  columns = []
  for column in data_copy.columns:
  data_copy[str(column)+'_vi_2'] = data_copy[column].apply(lambda x: 
                     x- sum(data_copy[column])/len(data_copy))
  vi_2_sum = sum(pow(data_copy[str(column)+'_vi_2'], 2))
  raida = np.sqrt(1/(len(data_copy)-1) * vi_2_sum)
  data_copy[column] = data_copy.apply(lambda x: np.nan 
                      if abs(x[str(column)+'_vi_2']) > 3*raida else x[column], axis=1)
  columns.append(str(column)+'_vi_2')
  data_copy.drop(columns = columns, inplace=True)
  return data_copy
# 以下是使用的样例，运行时间45分钟左右
columns_sample = ['job_num','videojob_num','test_avgscore',
                  'videojob_time','test_num','pv','work_num',
                  'work_avgscore','sign_num','exam_num']
raida_criterion(data.loc[:,columns_sample]) # 输入数值型指标所在的列名

2.1.3 类别特征处理

类别特征是指所在学院、专业、班级等在有限类别内取值的特征。它的原始输入通常是字符串形式，为了方便后续的构建模型，必须对类别特征做一定的处理，转换成可靠的数值特征才能正确运行。常见的类别特征的处理方法有：独热编码(one-hot encoding)、序列编码(ordinal encoding)、二进制编码(binary encoding)和统计编码。

• 独热编码：0、1编码方式，如：[男，女] => [[1,0], [0, 1]]
• 序列编码：适用于类别之间的距离具有相同的含义，如：[大一, 大二, 大三, 大四] => [0, 1, 2, 3]。
• 二进制编码：先使用序列编码转化为数值形式，再将数值转化为二进制的方式。
• 统计编码：统计各类别在训练集中出现的频率，并将频率作为新的特征。

由于学院、专业、专业班级、课程、课程班级和学年的类别数较多，采用独热编码会带来稀疏性的问题（可在利用特征选择的技巧降低维数），故这里采用序列编码；其余三种编码方式可以自行探索。代码如下：

from sklearn.preprocessing import LabelEncoder
category_columns = ['department_name', 'major_id', 'class_id',
                    'course_id', 'clazz_id', 'school_year']
for column in category_columns:
  data[column] = LabelEncoder().fit_transform(data[column])

2.1.4 特征生成

在2.1.1中提到update_time可以看作学生的学习特性，也就是假定某一时间为该学生常规的学习时间，利用update_time生成week (按周划分学习时间)、month (按月划分学习时间) 、 is_workday(划分周末或工作日学习) 、morning_afternoon_night_other(将学习时间分为早、中、晚及其余工作时间)四个新的学习行为特征，随后删除无法数值化的时间类型指标，代码如下：

data['week'] = data.apply(lambda x: pd.to_datetime(x['update_time']).weekday()+1, axis=1)
data['is_workday'] = data.apply(lambda x: 0 if x['week'] in [6, 7] else 1, axis=1)
data['month'] = data.apply(lambda x: pd.to_datetime(x['update_time']).month, axis=1)
data['MANO'] = data.apply(lambda x: (pd.to_datetime(x['update_time']) - pd.to_datetime('2020-01-01 00:00:00')).seconds, axis=1)
# 划分「早、中、晚、其他」时间的函数
# 各个时间点所代表的时间戳: 8:00/28800 12:00/43200 13:00/46800 17:00 61200 18:00/64800 22:00/79200
def divide_time(t):
  if t>=28800 and t<=43200:
    return 0
  elif t>=46800 and t<=61200:
    return 1
  elif t>=64800 and t<=79200:
    return 2
  else:
    return 3
data['MANO'] = data['MANO'].apply(lambda x: divide_time(x)) 
data = data.drop(columns=['update_time'])

经过上述操作后，数据的变化情况为 54788 * 18​ => 54788 * 21​。

2.1.5 成绩标签划分

为了具体判断 12 种学习行为指标、6 种基本信息指标和 2 种其他信息指标对成绩的影响程度，同时实现通过学生的这些指标来对其最终成绩进行预测，于是对数据进行探索发现所有样本中的最低分为1分，最高分为160分，故本部分从分类的角度出发，将学生的成绩分为 5 个级别：0-69 分、 70-79 分、80-89 分、90-100 分、101-160分。代码如下：

print(min(data.exam_avgscore)) # 1.0
print(max(data.exam_avgscore)) # 160.0
def exam_score_label(s):
        if s>=0 and s<=69:
            return 1
        elif s>=70 and s<=79:
            return 2
        elif s>=80 and s<=89:
            return 3
        elif s>=90 and s<=100:
            return 4
        else:
            return 5
data['label'] = data['exam_avgscore'].apply(lambda x: exam_score_label(x))
data = data.drop(columns=['exam_avgscore']) 
# data.label.value_counts() 查看各分数段的样本数量

将各分数段样本（学生）的数量占总样本（学生）的比例画成饼状图如下，代码见附录(3)：

从上图可以看出80-90分之间的样本数量占比最多，除了101-160分之间的样本，其他4个分数段的样本数量分布较为均衡。

2.2 特征选择

特征选择是指从全部特征中选取一个特征子集，使构造出来的模型更好。在机器学习的实际应用中，特征数量往往较多，其中可能存在不相关的特征，特征之间也可能存在相互依赖，而特征个数越多，容易引起“维度灾难”，模型也会越复杂，其推广能力会下降。

2.2.1 相关性分析

在选取的特征中，每个特征对于成绩的影响程度不同，因此为了提升特征对成绩预测的预测精度，同时避免一些指标对结果的负面影响，本节以考试平均成绩exam_avgscore为变量，与各个特征进行相关性分析。

(1) Pearson相关系数：
Pearson 相关系数可以理解为数据 (X 与 Y 的协方差) ​ (X的标准差​ Y的标准差)，具体的结果如下，代码见附录(4)：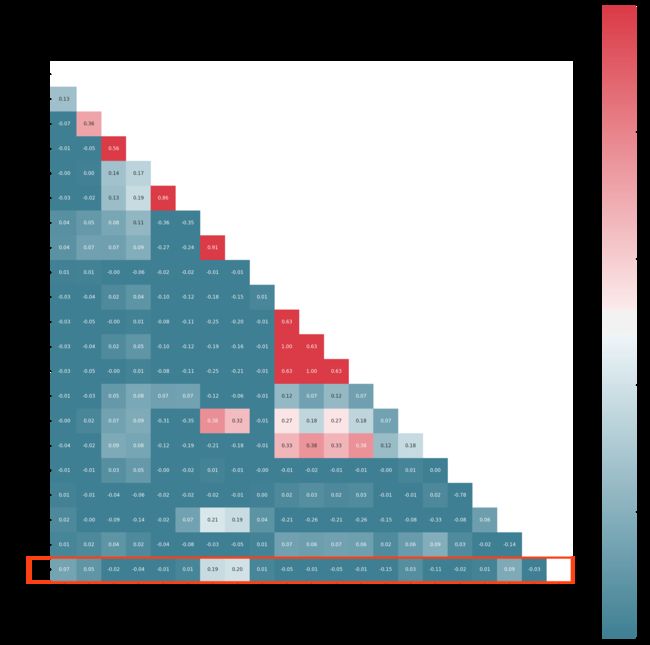
从上图红色方框可以看出，job_num、videojob_num、month、department_name这四个指标与成绩之间的相关性比较高，此时由于特征数量不多，故不进行特征选择。

(2) Spearman相关系数：
Spearman相关性系数，通常也叫斯皮尔曼秩相关系数。“秩”可以理解成就是一种顺序或者排序，那么它就是根据原始数据的排序位置进行求解，具体结果如下，代码同附录(4) 只需要替换其中的corr的值即可：

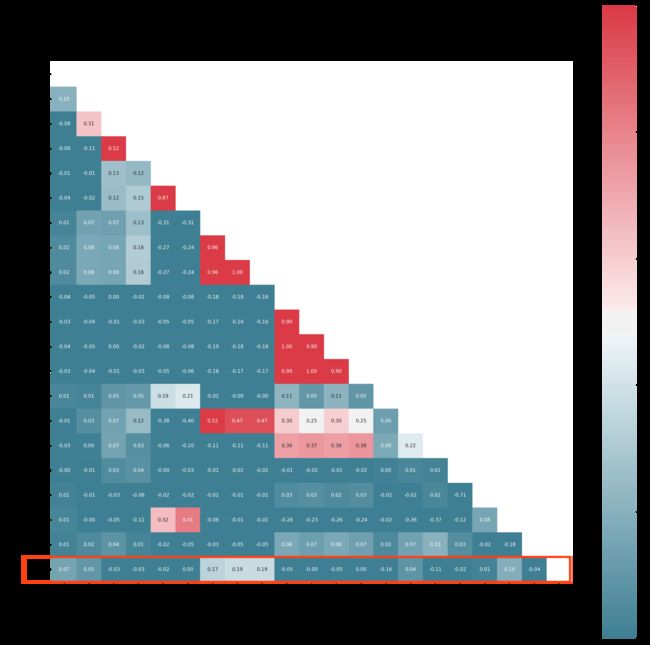
由红色方框可知，job_num、videojob_num、videojob_time、month、department_name这五个指标与成绩之间的相关性比较高，此时由于特征数量不多，故不进行特征选择。

2.2.2 降维

降低数据维度一般有两种思路：一是仅保留原始数据集中与目标变量最相关的变量；二是寻找一组较小的新变量，其中每个变量都是输入变量的组合，包含与输入变量基本相同的信息。本节从这两个角度分别进行实验。

(1) 基于随机森林Gini重要性排名的降维方法：

随机森林是一种集成学习算法，将会在「建模和评估」中讲解，本节提前使用它是为了保证整体流程的顺畅性，Gini重要性的通俗理解为：查看每个特征在随机森林中的每颗树上做了多大的贡献，然后取个平均值，最后比较特征之间的贡献大小，该算法可以通过设定阈值的方法将特征筛选至指定维度(如，只要重要性排名为前5的特征)，代码如下：

from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.ensemble import RandomForestClassifier 
​
x = data.iloc[:, 0:20] # 特征
y = data.label.values # 标签
# 以7:3的比例划分数据集，分为训练集和测试集
data_process = train_test_split(x, y, test_size=0.3, random_state=2021)
ss = StandardScaler() # 标准化处理
x_train_scaled = ss.fit_transform(data_process[0])
x_test_scaled = ss.transform(data_process[1])
y_train = np.array(data_process[2])
# 随机森林构建
rfc = RandomForestClassifier()
rfc.fit(x_train_scaled, y_train)
rfc.score(x_train_scaled, y_train)
# Gini重要性的计算
feats = {
     }
for feature, importance in zip(x.columns, rfc.feature_importances_):
  feats[feature] = importance
  importances = pd.DataFrame.from_dict(feats, orient='index').rename(columns={
     0: 'Gini-Importance'})
  importances = importances.sort_values(by='Gini-Importance', ascending=False)
  importances = importances.reset_index()
  importances = importances.rename(columns={
     'index': 'Features'})
# 找出排名靠后的15个特征
columns_del = list(importances['Features'][5:].values)
# x = x.drop(columns=columns_del) # 如果需要删除这些特征，才运行该行代码

利用该方法找出前五重要的特征为：pv、clazz_id、class_id、week、 major_id，做到这一步，已经能做出一些猜想了，比如，学生的成绩与他们访问在线学习平台的次数有着重要的联系，专业班和教学班的整体氛围可能也会影响学生的学业成绩，不同的专业对于学生的成绩可能也有一定的影响等等。特征的Gini重要性排名的可视化结果如下，代码见附录(5)：

(2) 基于主成分分析(PCA)的降维方法：

PCA(Principal Component Analysis)是一种常见的高维数据的降维方式，可用于提取数据的主要特征分量。对归一化后的20个特征进行降维，寻找可以代替原特征的一组维数更少的新特征，代码如下：

from sklearn.decomposition import PCA # 其他包按需导入
​
pca = PCA(n_components=20)
pca.fit(x_train_scaled) # 注意：此时选用的是归一化后的特征
# 绘制累计解释方差图
plt.rcParams['font.sans-serif'] = ['Songti SC']
plt.rcParams['axes.unicode_minus'] = False 
sns.set(font = 'Songti SC', style='whitegrid')
plt.plot(list(range(1,21)), np.cumsum(pca.explained_variance_ratio_)) # 累积解释方差
plt.xlabel('特征数量', fontsize=10, weight = 'bold')
plt.xticks(list(range(1,21)))
plt.ylabel('累积解释方差', fontsize=10, weight = 'bold')
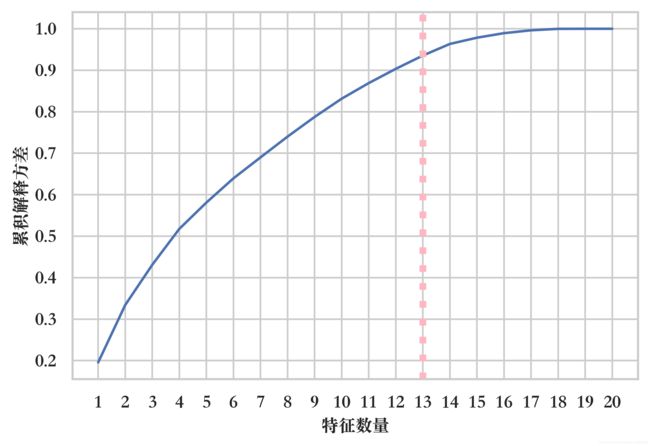
plt.axvline(linewidth=4, color='lightpink', linestyle=':', x=13, ymin=0, ymax=1)

经实验可知，当特征数量达到 17 个时，累积解释方差已经完全收敛，在超过 13 个特征之后，实验并未获得太多的解释方差，此时的累积解释方差率为 93.54%，这意味着当使用 PCA 将 20 个预测变量减少到 13 个分量时，仍然可以解释 93.54% 以上的方差，其他 7 个分量仅解释了不到 7% 的方差，因此本研究可以减少它们的权重。

本节只提供了两种降维的思路，并没有实际删除特征或者更改特征，这是因为删除的特征数量不同会给实验带来不同的效果，具体阈值的选取在建模部分会展开介绍。

3 建模和评估

本部分利用上述两章的数据构建学生在线学习成绩的预测模型，该问题的本质是分类，也就是说在2.1.5中，将学生的期末成绩划分出了5类标准，任务要做的是通过学生的多种特征来判定这个学生最终能够获得什么样的分数。机器学习中有许多的分类模型可以直接使用，比如本部分的研究思路是对比多种分类算法在本数据集上的效果，选出最优的模型并进行超参数调整，随后结合不同的降维算法做进一步的对比实验，最终给出每一种类别的分类评价。

3.1 分类模型构建

3.1.1 模型的选择

在未进行分类之前，我并不了解哪种分类算法适用于本项目的数据集，所以我需要使用多种算法进行对比，而算法效果的优劣需要有对应的指标来进行评价，采用的分类算法有：KNN、朴素贝叶斯(GaussianNB & BernoulliNB)、决策树、支持向量机、随机森林和AdaBoost，采用的分类算法评价指标有：准确率、召回率、精准率和F1分数。为了突出重点，隐藏了sklearn_model_Classification(feature, label)函数整体的实现细节，具体细节见附录(6)，而评价指标将在模型的效果评估中进行简单介绍。

feature = data.iloc[:, 0:20] # 选取特征
label = data.label.values # 选取标签
models, acc, recall, precision = sklearn_model_Classification(feature, label) # 附录(6)
res = pd.DataFrame(models,columns=['models'])
res['Accuracy'] = acc
res['Recall'] = recall
res['Precision'] = precision
res['F1_Score'] = res.apply(lambda x: 2*(x['Recall']*x['Precision'])/(x['Recall']+x['Precision']),axis=1) # 展示分类的效果

模型运行的过程需要花费一定时间，随后各分类算法的效果如下，代码见附录(7)：
从图中很容易看出，基于集成学习方法的随机森林对于本数据集拥有最佳的分类性能，细心的小伙伴可能发现了，我进行模型选择的过程中，存在两个问题：

• 实验没有对数据进行标准化
• 实验没有用到2.2节中介绍的特征选择

3.1.2 随机森林模型

在进一步实验之前，先介绍一下随机森林，随机森林是基于集成学习的思想，将多颗树集成在一起的算法，它的基本单元是决策树，且这些决策树之间彼此独立没有关联。随机森林的具体构建过程如下：

1. 从原始样本集中使用 Bootstraping 方法进行​ 次随机有放回采样，选出 m 个训练样本，得到​个训练集。
2. 对于​个训练集，分别训练​个决策树模型。
3. 假设单个决策树模型需要训练的特征个数为 n，决策树每次分裂时比较信息增益、信息增益比、基尼指数三个指标值最好的特征进行分裂。
4. 循环步骤 3 中的分裂过程， 直到该分裂节点的所有训练样本成为同一类。在随机森林中，单个决策树在分裂过程中不需要剪枝。
5. 最后，随机森林由生成的决策树组合而成。 对于分类问题， 按多棵决策树分类器投票决定最终分类结果。

具体实验步骤如下：

• 首先，对所有特征进行标准化处理；
• 接着，对原特征进行2.2.2中的PCA降维，以“累计方差解释率大于90%且小于100%”的成分选取标准来选取主要成分，并对比不同成分数量(12、13、14、15、16、17、18、19)和原数据中模型的效果；
• 最后，根据Gini重要性的排名，分别选取前25%、35%、45%、55%、65%、75%、100%的特征进行对比实验。实验以7:3的比例划分训练集和测试集，在测试集中验证模型的效果。

（1）基于PCA的对比实验

from sklearn.preprocessing import StandardScaler
from sklearn.ensemble import RandomForestClassifier 
from sklearn.decomposition import PCA
from sklearn.metrics import accuracy_score, recall_score, precision_score
​
feature_ss = StandardScaler().fit_transform(feature) # 对特征进行标准化, label同2.1.1
components = [12, 13, 14, 15, 16, 17, 18, 19, 20] # 根据2.2.2节中得到的结果
evaluation = [[], [], [], []] # 用于保存4个评价指标
RF = RandomForestClassifier()
for i in components:
  pca = PCA(n_components=i)
  feature_ss_pca = pca.fit_transform(feature_ss)
  # feature_RF <=> [feature_train, feature_test, label_train, label_test]
  data_RF= train_test_split(feature_ss_pca, label, test_size=0.3) # 划分训练集和测试集7:3
  RF.fit(data_RF[0], data_RF[2]) # 拟合训练集
  label_pred = RF.predict(data_RF[1]) # 预测测试集
  acc = accuracy_score(data_RF[3], label_pred)
  recall = recall_score(data_RF[3], label_pred,average="macro")
  precision = precision_score(data_RF[3], label_pred,average="macro")
  f1 = 2*recall*precision/(recall+precision)
  tmp = [acc, recall, precision, f1]
  for i, j in zip([0,1,2,3], tmp):
    evaluation[i].append(j)

（2）基于Gini重要性的对比实验

#根据2.2.2节中得到的排序，比如14为'pv'在原始数据中的列号，列从0开始计数
feature_25 = feature_ss[:,[14,5,2,16,4]] # feature_ss为已经过标准化后的特征数据
feature_35 = feature_ss[:,[14,5,2,16,4,1,19]]
feature_45 = feature_ss[:,[14,5,2,16,4,1,19,12,10]]
feature_55 = feature_ss[:,[14,5,2,16,4,1,19,12,10,15,6]]
feature_65 = feature_ss[:,[14,5,2,16,4,1,19,12,10,15,6,0,7]]
feature_75 = feature_ss[:,[14,5,2,16,4,1,19,12,10,15,6,0,7,8,13]]
feature_Gini = [feature_25, feature_35, feature_45, feature_55, feature_65, feature_75, feature_ss]
evaluation_Gini = [[], [], [], []]
RF = RandomForestClassifier()
for f in feature_Gini:
  data_RF= train_test_split(f, label, test_size=0.3) # 划分训练集和测试集7:3
  RF.fit(data_RF[0], data_RF[2]) # 拟合训练集
  label_pred = RF.predict(data_RF[1]) # 预测测试集
  acc = accuracy_score(data_RF[3], label_pred)
  recall = recall_score(data_RF[3], label_pred,average="macro")
  precision = precision_score(data_RF[3], label_pred,average="macro")
  f1 = 2*recall*precision/(recall+precision)
  tmp = [acc, recall, precision, f1]
  for i, j in zip([0,1,2,3], tmp):
    evaluation_Gini[i].append(j)

上述两种模型都是基于随机森林算法实现的，具体的实验效果如下，代码见附录(8)：

左图代表基于PCA的随机森林算法，当PCA后的成分数为20时，模型的准确率、召回率、精准率和F1分数均最高，分别为0.539、0.427、0.445、0.436；右图代表基于Gini重要性特征筛选的随机森林算法，当选取前75%个，模型的综合性能最好，此时的准确率、召回率、精准率和F1分数分别为0.555、0.4398、0.440、0.4399，PCA后的模型效果。从实验效果来看，PCA后的随机森林算法相比较未进行PCA前效果有所降低，而选取前75%的特征能够使模型在默认参数设置下达到最佳状态。

3.1.3 超参数调整

为了进一步提升预测效果，我们选取标准化后Gini重要性排名前 75% 的特征对随机森林算法进行超参数调整，算法对于每一个数据集都有着独特的最优参数，选定一组最优的参数有助于发挥模型的最大性能。超参数调整从两个角度出发，先进行随机搜索（RandomSearchCV）后进行网格搜索（GridSearchCV）。

首先从随机搜索来开始考虑更多的超参数，首先将其传入随机森林模型中，然后传入参数字典中、测试迭代次数以及交叉验证次数，代码如下(注意，超参数的代码运行时间较长)：

from sklearn.model_selection import RandomizedSearchCV
# 对如下6个超参数进行随机搜索
data_RS = train_test_split(feature_75, label, test_size=0.3) # 划分训练集和测试集7:3
n_estimators = [int(x) for x in np.linspace(start = 100, stop = 1000, num = 10)]
max_features = ['log2', 'sqrt']
max_depth = [int(x) for x in np.linspace(start = 1, stop = 15, num = 15)]
min_samples_split = [int(x) for x in np.linspace(start = 2, stop = 50, num = 10)]
min_samples_leaf = [int(x) for x in np.linspace(start = 2, stop = 50, num = 10)]
bootstrap = [True, False]
param_dist = {
     'n_estimators': n_estimators,'max_features': max_features,
              'max_depth': max_depth,'min_samples_split': min_samples_split,
              'min_samples_leaf': min_samples_leaf,'bootstrap': bootstrap}
RFC = RandomForestClassifier()
RFC.fit(data_RS[0], data_RS[2])
RS = RandomizedSearchCV(RFC, param_dist, n_iter=100, cv=3, verbose=1, 
                        n_jobs=-1, random_state=0) # 3折交叉验证，迭代100次
RS.fit(data_RS[0], data_RS[2])
# print(RS.best_params_) # 打印随机搜索的最佳参数
# 构造超参数随即搜索结果DataFrame, 用于可视化。
RSD=pd.DataFrame(rs.cv_results_).sort_values('rank_test_score').reset_index(drop=True)
RSD=RSD.drop(['mean_fit_time', 'std_fit_time','mean_score_time','std_score_time','params','split0_test_score','split1_test_score', 'split2_test_score', 'std_test_score'], axis=1)

为了清晰的展现挑选超参数的过程，我们将整个过程用可视化的方式展现，代码见附录(9)：

经过随机搜索得到的一组最优参数为n_estimators: 600, min_samples_split: 23, min_samples_leaf': 2, max_features: sqrt, max_depth: 15, bootstrap: False，针对上图的结果，我们利用网格搜索进行进一步的微调，代码如下：

from sklearn.model_selection import GridSearchCV
# 根据随即搜索的结果设置网格搜索的参数列表
n_estimators = [700,900]
max_features = ['sqrt','log2']
max_depth = [11,12,13,14,15]
min_samples_split = [23,28,44]
min_samples_leaf = [18,34,44]
bootstrap = [False]
param_grid = {
     'n_estimators':n_estimators, 'max_features':max_features,
              'max_depth': max_depth, 'min_samples_split':min_samples_split,
              'min_samples_leaf':min_samples_leaf, 'bootstrap':bootstrap}
GS = GridSearchCV(RFC, param_grid, cv=3, verbose=1, n_jobs=-1)
GS.fit(data_RS[0], data_RS[2])
RFC_GS = GS.best_estimator_ # RFC_GS即为最终的模型

最终选定的最优参数为如下表：

参数名	值	参数名	值
n_estimators	700	max_features	‘sqrt’
min_samples_split	23	max_depth	15
min_samples_leaf	18	bootstrap	False

3.2 模型效果评估

我们如何判断模型是否适用于一个数据集？显然需要对模型进行评估。在分类任务中，3.1节中使用的准确率、召回率、精准率和F1分数就是常见的分类算法评价指标，它们的具体含义如下：

• 准确率：指分类器正确预测的样本数量占被预测样本总数量的比例。
• 召回率：指分类器中所有被预测为正的样本中实际为正的样本的比例。
• 精准率：指分类器中实际为正的样本中同时预 测也为正样本的比例。
• F1分数：它是由于召回率和精准率两者之间难以达到一个平衡点而发明的一个指标， 该指标的值越大越好。

对于上节选定的最优参数下的模型，再对数据进行一次分类，此时得到的准确率、召回率、精准率和F1分数分别为0.573、0.439、0.452、0.446，相比较未进行调优前有了略微的提升，总体效果还是让人不够满意，预测模型的好坏很大程度上取决于数据本身的质量，换句话说，数据决定了模型的上限，算法只是逼近这个上限而已。

虽然整体的效果一般，但是可以通过混淆矩阵来查看每一个类的分类效果，代码如下：

from sklearn.metrics import confusion_matrix
# 构建混淆矩阵
RFC_GS.fit(data_RS[0], data_RS[2])
y_pred_tune = RFC_GS.predict(data_RS[1])
conf_matrix = pd.DataFrame(confusion_matrix(data_RS[3], y_pred_tune), 
                           index = ['0-69', '70-79', '80-89', '90-100', '100-160'], 
                           columns = ['0-69', '70-79', '80-89', '90-100', '100-160'])
print(conf_matrix) # 打印混淆矩阵
# 计算模型的总体效果
acc = accuracy_score(data_RS[3], y_pred_tune)
recall = recall_score(data_RS[3], y_pred_tune,average="macro")
precision = precision_score(data_RS[3], y_pred_tune,average="macro")
f1_score = 2*recall*precision/(recall+precision)
# 计算每个类的评价指标
conf_evalution = conf_matrix
conf_evalution['Accuracy'] = np.zeros(5)
for i in range(5):
  conf_evalution['Accuracy'][i]=conf_evalution.iloc[i, [i]]/sum(conf_evalution.iloc[i, :])

由此得到的混淆矩阵如下：

	0-69	70-79	80-89	90-100	101-160
0-69	3474	220	600	180	0
70-79	746	703	1507	320	0
80-89	544	381	3456	758	0
90-100	234	93	1239	1780	0
101-160	61	22	90	29	0

从混淆矩阵可以看出101-160这个类我们的模型没有一次预测准确，原因在于这个类别的数量极少，模型没能学习到相应特征的细节，所以后续还探讨类别不平衡的问题，这里就不再介绍了，最后给出每个类的分类效果如下：

类别	0-69	70-79	80-89	90-100	101-160
准确率	0.776	0.215	0.673	0.532	0

由此可以得出0-69分这一类的分类效果最好，其次是80-89分这一类，在2.1.5中得知。类别101-106分的样本数量极少，所以模型没能识别出它们独特的特征也是合理的。

附录

(1) 各学院产生的学生行为记录数图

import matplotlib.pyplot as plt
## 生成画图的数据
pic = pd.DataFrame(data.department_name.value_counts()).rename(columns={
     'department_name':'sum'}) 
## 图像绘制
plt.rcParams['savefig.dpi'] = 600 # 图像像素
plt.rcParams['figure.dpi'] = 600 # 图像分辨率 
plt.rcParams['font.sans-serif'] = ['Songti SC'] # mac OS系统中设置的中文字体
plt.rcParams['axes.unicode_minus'] = False 
fig, ax = plt.subplots()
plt.figure(figsize=(6,6))
b = ax.barh(list(pic.index), pic['sum'], color='skyblue')
# 添加数据标签
for rect in b:
  w = rect.get_width()
  ax.text(w, rect.get_y()+rect.get_height()/2, '%d'%int(w), ha='left', va='center',fontsize=9)
#设置Y轴刻度线标签
ax.set_xticks([0,1000,2000,3000,4000,5000,6000,7000,8000])
ax.set_xticklabels([0,1000,2000,3000,4000,5000,6000,7000,8000],fontsize=9)
ax.set_yticks(range(len(list(pic.index))))
ax.set_yticklabels(list(pic.index), fontsize=9)
ax.set_title('18个学院的样本数(处理后)',fontsize=12, weight='bold')

(2) 各学院的平时测验成绩平均分和期末成绩平均分对比图

import matplotlib.pyplot as plt
import numpy as np
## 生成画图的数据
data_new = data[data['test_avgscore']!=0].reset_index(drop=True)
pic2 = data_new.groupby('department_name')['test_avgscore'].mean().reset_index()
pic2['exam_avgscore'] = data_new.groupby('department_name')['exam_avgscore'].mean().reset_index()['exam_avgscore']
## 图像绘制
plt.rcParams['savefig.dpi'] = 600 # 图像像素
plt.rcParams['figure.dpi'] = 600 # 图像分辨率 
plt.rcParams['font.sans-serif'] = ['Songti SC']
plt.rcParams['axes.unicode_minus'] = False   
x = pd.Series(np.arange(1,19,1))
y1 = pic2['exam_avgscore']
y2 = pic2['test_avgscore']
total_width, n = 0.8, 2
width = total_width / n
plt.figure(figsize=(15,5))
plt.bar(x, y1-60, color='lightpink', width=width, label = "调整后的考试平均分")
plt.bar(x+width, y2-60, color='skyblue', width=width, label = "调整后的测试平均分")
plt.tick_params(labelsize=9)
plt.xticks(x+width/2,x)
plt.grid()
plt.legend()

(3) 成绩标签划分后的分布

import seaborn as sns 
## 生成画图的数据
categories = data.label.value_counts()
categories = categories.reset_index().sort_values('index')
categories['index'] = ['0-69分', '70-79分', '80-89分', '90-100分', '101-160分']
categories = dict(zip(categories['index'].values, categories['label'].values))
title = '成绩标签划分后的分布'
## 图像绘制
sns.set_palette(sns.color_palette('Paired', n_colors=len(categories)))
plt.rcParams['savefig.dpi'] = 600 # 图像像素
plt.rcParams['figure.dpi'] = 600 # 图像分辨率 
plt.rcParams['font.sans-serif'] = ['Songti SC'] 
plt.figure(figsize=(16,6))
categories_label = [y for y in list(categories.keys())]
categories = dict(sorted(categories.items(), key=lambda x:x[1], reverse=True))
explode=[0 for _ in range(len(categories))]
explode[0]=0.05
plt.pie(categories.values(), labels=categories_label, autopct='%3.1f%%', explode=explode)
plt.legend(loc='best', bbox_to_anchor=(0.1, 0.4))
plt.title(title,fontsize=18, weight='bold')

(4) 相关系数热力图

import seaborn as sns
import numpy as np
import matplotlib.pyplot as plt
## 生成画图的数据
corr= data.corr(method='pearson')
# corr = data.corr(method='spearman')
## 图像绘制
mask = np.zeros_like(corr, dtype=np.bool)  # 构造与mcorr同维矩阵为bool型
mask[np.triu_indices_from(mask)] = True  # 角分线右侧为True
plt.figure(figsize=(24,24),dpi=200)
cmap = sns.diverging_palette(220, 10, as_cmap=True)  # 返回matplotlib colormap对象
g = sns.heatmap(corr, mask=mask, cmap=cmap, square=True, annot=True, vmax=0.4, vmin=0, fmt='0.2f')  # 热力图
plt.show()

(5) 特征的Gini重要性排名

import matplotlib.pyplot as plt
import seaborn as sns
## 数据用importances
## 图像绘制
sns.set(font='Songti SC',style="whitegrid", color_codes=True, font_scale=1.7)
fig, ax = plt.subplots()
fig.set_size_inches(30,15)
fg = sns.barplot(y=importances['Features'], x=importances['Gini-Importance'], data=importances, color='skyblue')
plt.xlabel('重要性', fontsize=25, weight = 'bold')
plt.ylabel('特征', fontsize=25, weight = 'bold')
plt.title('特征的Gini重要性', fontsize=25, weight = 'bold')
fig = fg.get_figure()
fig.savefig("../Gini重要性.png", dpi=600)

(6) 分类模型选择函数

def sklearn_model_Classification(feature,label):
    from sklearn.model_selection import train_test_split
    feature_train, feature_test, label_train, label_test = train_test_split(feature, label, test_size=0.1)
    from sklearn.metrics import accuracy_score, recall_score, precision_score
    from sklearn.neighbors import  KNeighborsClassifier
    from sklearn.naive_bayes import GaussianNB, BernoulliNB
    from sklearn.tree import DecisionTreeClassifier
    from sklearn.svm import SVC
    from sklearn.ensemble import RandomForestClassifier, AdaBoostClassifier  
    models = []
    acc = []
    recall = []
    precision = []
    models.append(("KNN",KNeighborsClassifier(n_neighbors=2)))
    models.append(("GaussianNB",GaussianNB()))
    models.append(("BernoulliNB",BernoulliNB()))
    models.append(("DecisionTreeGini",DecisionTreeClassifier()))
    models.append(("DecisionTreeEntropy",DecisionTreeClassifier(criterion="entropy")))
    models.append(("SVM Classifier",SVC(C=100)))
    models.append(("RandomForest",RandomForestClassifier()))
    models.append(("Adaboost",AdaBoostClassifier(n_estimators=100)))
    for classify_name, classify in models:
        classify.fit(feature_train,label_train)
        feature_label_list = [(feature_test,label_test)]
        feature_part = feature_label_list[0][0]
        label_part = feature_label_list[0][1]
        label_pred = classify.predict(feature_part)
        acc.append(accuracy_score(label_part, label_pred))
        recall.append(recall_score(label_part, label_pred,average="macro"))
        precision.append(precision_score(label_part, label_pred,average="macro"))
    for i in range(len(models)):
        models[i] = models[i][0]
    return models, acc, recall, precision

(7) 分类效果评价图

plt.rcParams['savefig.dpi'] = 600 # 图像像素
plt.rcParams['figure.dpi'] = 600 # 图像分辨率 
plt.rcParams['font.sans-serif'] = ['Songti SC'] 
x = pd.Series(np.arange(1,9,1))
total_width, n = 0.8, 4
width = total_width/n
plt.figure(figsize=(15,5))
plt.bar(x, res['Accuracy'], color='red', width=width, label='Accuracy')
plt.bar(x+width, res['Recall'], color='blue', width=width, label='Recall')
plt.bar(x+2*width, res['Precision'], color='green', width=width, label='Precision')
plt.bar(x+3*width, res['F1_Score'], color='grey', width=width, label='F1_Score')
plt.title('分类模型效果', fontsize=18, weight='bold')
plt.tick_params(labelsize=9)
plt.xticks(x+1.5*width, res['models'])
plt.grid()
plt.legend()

(8) 随机森林模型实验

# 基于PCA的随机森林
X = [i for i in range(12,21)]
evaluation = evaluation_PCA
#X = [i for i in range(0,7)] # 基于Gini重要性的随机森林
#evaluation = evaluation_Gini
plt.rcParams['savefig.dpi'] = 600 #图片像素
plt.rcParams['figure.dpi'] = 600 #分辨率
sns.set(font = 'Songti SC', style='whitegrid')
plt.plot(X, evaluation[0], color='blue',marker = '^', label = 'Accuarcy')
plt.plot(X, evaluation[1], color='red', marker = 'o', label = 'Recall')
plt.plot(X, evaluation[2], color='green', marker = '*', label = 'Precision')
plt.plot(X, evaluation[3], color='cyan', marker = '+', label = 'F1-Score')
plt.ylabel('Evaluation Score', fontsize=11)
plt.xticks(X)
# plt.xticks(X,['25%', '35%', '45%', '55%', '65%', '75%', '100%'])
plt.legend(loc = 'center right', bbox_to_anchor=(0.5, 0.45, 0.5 , 0.5))

(9) 超参数随机搜索实验

# 自行导入包
fig, axs = plt.subplots(ncols=3, nrows=2)
sns.set(style="whitegrid", color_codes=True, font_scale=2)
fig.set_size_inches(30,25)
sns.barplot(x='param_n_estimators', y='mean_test_score', data=RSD, ax=axs[0,0], color='pink')
axs[0,0].set_ylim([.46,.55])
axs[0,0].set_title(label = 'n_estimators', size=30, weight='bold')
sns.barplot(x='param_min_samples_split', y='mean_test_score', data=RSD, ax=axs[0,1], color='red')
axs[0,1].set_ylim([.46,.55])
axs[0,1].set_title(label = 'min_samples_split', size=30, weight='bold')
sns.barplot(x='param_min_samples_leaf', y='mean_test_score', data=RSD, ax=axs[0,2], color='skyblue')
axs[0,2].set_ylim([.45,.55])
axs[0,2].set_title(label = 'min_samples_leaf', size=30, weight='bold')
sns.barplot(x='param_max_features', y='mean_test_score', data=RSD, ax=axs[1,0], color='wheat')
axs[1,0].set_ylim([.49,.52])
axs[1,0].set_title(label = 'max_features', size=30, weight='bold')
sns.barplot(x='param_max_depth', y='mean_test_score', data=RSD, ax=axs[1,1], color='grey')
axs[1,1].set_ylim([.39,.57])
axs[1,1].set_title(label = 'max_depth', size=30, weight='bold')
sns.barplot(x='param_bootstrap',y='mean_test_score', data=RSD, ax=axs[1,2], color='green')
axs[1,2].set_ylim([.49,.52])
axs[1,2].set_title(label = 'bootstrap', size=30, weight='bold')

(10) 数据的保存

RSD.to_excel('../中间结果数据/随即搜索超参数.xlsx',index=None)
feature.to_excel('../中间结果数据/处理后的特征数据.xlsx',index=None)
importances.to_excel('../中间结果数据/特征的Gini重要性排名.xlsx',index=None)
res.to_excel('../中间结果数据/模型选择结果.xlsx',index=None)
Gini_df = pd.DataFrame(evaluation_Gini,
                      index=['Accuarcy','Recall','Precision','F1_Score'],
                      columns=['25%', '35%', '45%', '55%', '65%', '75%', '100%'])
Gini_df.to_excel('../中间结果数据/GiniRF特征重要选择结果.xlsx')
PCA_df = pd.DataFrame(evaluation_PCA,
                     index=['Accuarcy','Recall','Precision','F1_Score'],
                     columns=[i for i in range(12,21)])
PCA_df.to_excel('../中间结果数据/PCA降维成分选择结果.xlsx')

写在最后：幸苦了幸苦了，这么长的文章读完也是不容易的一件事，数据处理的方法还有很多可以探究，本项目数据质量不是很好，如果有需要整个项目的数据，可以将「来意」发送至我的邮箱[email protected]，高校学生请备注学校+专业+姓名，通过后即可发送给你，继续努力撒～