【机器学习的数学基础】（八）矩阵分解(Matrix Decomposition)(下)

4 矩阵分解(Matrix Decomposition)(下)

4.6 矩阵逼近

我们认为奇异值分解是将一个矩阵分解为三个矩阵的乘积$\mathbf{A}=\mathbf{U}\mathbf{\Sigma }{\mathbf{V}}^{\top }\in {\mathbb{R}}^{m\times n}$的一种方法，其中$\mathbf{U}\in {\mathbb{R}}^{m\times m}$和$\mathbf{V}\in {\mathbb{R}}^{n\times n}$是正交的，$\mathbf{\Sigma }$主对角线上为奇异值。现在，我们将不进行完整奇异值分解(full SVD)，而是研究奇异值分解如何将矩阵$\mathbf{A}$表示为简单（低秩）矩阵${\mathbf{A}}_i$的和，这有助于采用比完整奇异值分解计算成本更低的矩阵近似方案。

我们构造秩1矩阵${\mathbf{A}}_i\in {\mathbb{R}}^{m\times n}$为：
$${\mathbf{A}}_i:={\mathbf{u}}_i{\mathbf{v}}_i^{\top }(4.90)$$
它由$\mathbf{U}$和$\mathbf{V}$的第$i$个正交列向量的外积构成。

图 4.11用SVD进行图像处理。(a)原始灰度图像是一个由0(黑)和1(白)之间的值组成的1,432 × 1,910的矩阵。(b) - (f)秩1矩阵${\mathbf{A}}_1,\dots ,{\mathbf{A}}_5$及其对应的奇异值${\sigma }_1,\dots ,{\sigma }_5$。每个秩1矩阵的网格状结构是由左奇异向量和右奇异向量的外积决定的。

秩为$r$的矩阵$\mathbf{A}\in {\mathbb{R}}^{m\times n}$能被写成秩1矩阵${\mathbf{A}}_i$ 的和：
$$\mathbf{A}=\sum _{i=1}^r{\sigma }_i{\mathbf{u}}_i{\mathbf{v}}_i^{\top }=\sum _{i=1}^r{\sigma }_i{\mathbf{A}}_i$$
其中，外积矩阵${\mathbf{A}}_i$权重为第$i$个奇异值${\sigma }_i$。

我们可以看出上式成立的原因：$\mathbf{A}=\mathbf{U}\mathbf{\Sigma }{\mathbf{V}}^{\top }$中，奇异值矩阵$\mathbf{\Sigma }$的对角结构仅将匹配的左右奇异向量作内积：${\mathbf{u}}_i{\mathbf{v}}_i^{\top }$，并用相应的奇异值${\sigma }_i$对它们进行缩放。对于$i\ne j$的项${\Sigma }_{ij}{\mathbf{u}}_i{\mathbf{v}}_j^{\top }$都消失了，因为$\mathbf{\Sigma }$除了对角线外都是0。任何$i>r$乘项都会消失，因为相应的奇异值也为0。

在(4.90)中，我们引入了秩-1矩阵${\mathbf{A}}_i$。我们将$r$个秩-1矩阵求和得到秩-$r$矩阵$\mathbf{A}$。如果这个和没有包括所有矩阵${\mathbf{A}}_i，i=1,\dots ,r$，而是$k<r$个时，我们得到的是$\mathbf{A}$的秩$k$逼近(rank-k approximation)：
$$\mathbf{A}(k):=\sum _{i=1}^k{\sigma }_i{\mathbf{u}}_i{\mathbf{v}}_i^{\top }=\sum _{i=1}^k{\sigma }_i{\mathbf{A}}_i$$
其中$\mathrm{rk}(\mathbf{A}(k))=k$。

图 4.12用SVD进行图像重建。(a)原始图像。(b) - (f)使用SVD的低秩逼近进行图像重建，其中秩k近似由$\mathbf{A}(k)={\sum }_{i=1}^k{\sigma }_i{\mathbf{A}}_i$给出。

图4.12显示了巨石阵原始图像$\mathbf{A}$的低阶逼近$\mathbf{A}(k)$。岩石的形状变得越来越明显，并且在等级5的近似值中可以清楚地识别出来。虽然原始图像需要$1,432\cdot 1,910=2,735,120$个数字，但秩5近似法只需要我们存储五个奇异值和五个左右奇异向量（每个向量分别含1432和1910个数字），总共$5\cdot (1,432+1,910+1)=16,715$个数字，为原始图像的0.6%多。

为了度量$\mathbf{A}$与其秩k近似$\mathbf{A}(k)$之间的差异（误差），我们需要用到范数这个概念。在解析几何中，我们已经在向量上使用了度量向量长度的范数。通过类比，我们也可以定义矩阵的范数。

定义 23矩阵的谱范数

对于$\mathbf{x}\in {\mathbb{R}}^n\backslash \{0\}$，矩阵$\mathbf{A}$的谱范数(Spectral Norm of a Matrix)定义为：
$$\Vert \mathbf{A}{\Vert }_2:=\underset{\mathbf{x}}{\max }\frac{\Vert \mathbf{A}\mathbf{x}{\Vert }_2}{\Vert \mathbf{x}{\Vert }_2}$$
我们在矩阵范数（左侧）中引入了下标的表示法，类似于向量的欧几里德范数（右侧）的下标2。谱范数决定了向量$\mathbf{x}$与$\mathbf{A}$相乘时，最多变得多长。

定理 4.24

$\mathbf{A}$的谱范数是其最大奇异值${\sigma }_i$。

定理 4.25 Eckart-Young 定理

考虑一个秩为$r$的矩阵$\mathbf{A}\in {\mathbb{R}}^{m\times n}$，令$\mathbf{B}\in {\mathbb{R}}^{m\times n}$为秩$k$的矩阵，对于$k\le r$的$\mathbf{A}(k)={\sum }_{i=1}^k{\sigma }_i{\mathbf{u}}_i{\mathbf{v}}_i^{\top }$，以下成立：
$$\mathbf{A}(k)={\mathrm{argmin}}_{\mathrm{r}\mathrm{k}(\mathbf{B})=k}\Vert \mathbf{A}-\mathbf{B}{\Vert }_2(4.94)$$
$$\Vert \mathbf{A}-\mathbf{A}(k){\Vert }_2={\sigma }_{k+1}(4.95)$$

Eckart-Young定理明确地说明了我们使用秩$k$逼近来逼近$\mathbf{A}$所引入的误差是多少。我们可以把用奇异值分解得到的秩$k$近似解释为满秩矩阵$\mathbf{A}$在秩最大为$k$的矩阵所在的低维空间上的投影。在所有可能的投影中，奇异值分解使$\mathbf{A}$和任何秩$k$逼近之间的（谱范数得到的）误差最小化。

Eckart-Young定理意味着我们可以使用奇异值分解（SVD）将秩$r$矩阵$\mathbf{A}$降为秩$k$矩阵$\mathbf{A}$，这是一种取主要成分并达到最优的（在谱范数意义上）方式。我们可以将秩$k$矩阵对$\mathbf{A}$的逼近解释为有损压缩的一种方法。因此，矩阵的低秩逼近出现在许多机器学习应用中，例如图像处理、噪声滤波和不适定问题的正则化。此外，它在降维和主成分分析中起着关键作用，我们将第十章中看到。

4.7 矩阵Phylogeny

“phylogenetic”一词描述了我们如何获取个体与群体之间的关系，并源于希腊语中的“tribe”和“source”。

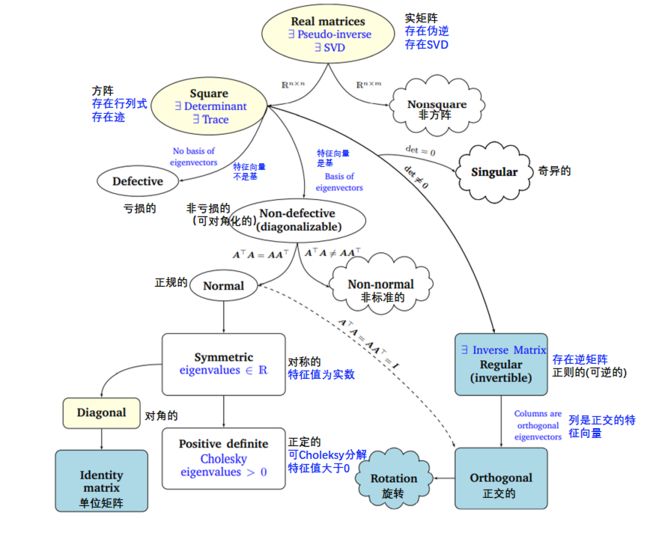
图4 .13与机器学习相关的矩阵的Phylogeny。

在第2章和第3章中，我们介绍了线性代数和解析几何的基础知识。在这一章中，我们研究了矩阵和线性映射的基本特征。图4.13描述了不同类型矩阵之间关系的Phylogeny（黑色箭头表示子集）以及我们可以对其执行的操作（蓝色）。

我们考虑所有实矩阵(real matrices)$\mathbf{A}\in {\mathbb{R}}^{n\times m}$。对于非方阵（其中$n\ne m$），奇异值分解总是存在的，正如我们在本章中看到的。以方阵(square matrices)$\mathbf{A}\in {\mathbb{R}}^{n\times n}$为中心，行列式告诉我们方阵是否具有逆矩阵(inverse matrix)，即它是否属于正则可逆矩阵类。如果平方$n\times n$矩阵具有$n$个线性无关的特征向量，则矩阵是非退化的(non-defective)，并且存在特征分解（定理4.12）。我们知道，重复的特征值可能导致矩阵退化，这种矩阵是不能对角化的。

非奇异矩阵和非退化矩阵是不同的。例如，旋转矩阵是可逆的（行列式是非零的），但不一定可对角化（特征值不能保证是实数）。

我们进一步研究了非退化$n\times n$方阵的分支。如果条件${\mathbf{A}}^{\top }\mathbf{A}=\mathbf{A}{\mathbf{A}}^{\top }$成立，则$\mathbf{A}$是正规的(normal)。此外，如果更严格的条件${\mathbf{A}}^{\top }\mathbf{A}=\mathbf{A}{\mathbf{A}}^{\top }=\mathbf{I}$成立，则$\mathbf{A}$称为正交（orthogonal,见定义3.8）。正交矩阵集是正则（可逆）矩阵的子集，满足${\mathbf{A}}^{\top }={\mathbf{A}}^{-1}$。

正规矩阵有一个常见的子集，即对称矩阵$\mathbf{S}\in {\mathbb{R}}^{n\times n}$，它满足$\mathbf{S}={\mathbf{S}}^{\top }$。对称矩阵只有实特征值。对称矩阵的子集由正定矩阵$\mathbf{P}$组成，正定矩阵$\mathbf{P}$对所有$\mathbf{x}\in {\mathbb{R}}^n\backslash \{0\}$满足${\mathbf{x}}^{\top }\mathbf{P}\mathbf{x}>0$的条件。在这种情况下，存在唯一的Cholesky分解（Cholesky decomposition，定理4.18）。正定矩阵只有正特征值且总是可逆的（即，具有非零行列式）。

对称矩阵的另一个子集由对角矩阵(diagonal matrices)$\mathbf{D}$组成。对角矩阵在乘法和加法下是闭合的，但不一定形成一个群（只有当所有的对角项都不为零时才是这种情况，这样矩阵才是可逆的）。一种特殊的对角矩阵是单位矩阵$\mathbf{I}$。

翻译自：
《MATHEMATICS FOR MACHINE LEARNING》作者是 Marc Peter Deisenroth，A Aldo Faisal 和 Cheng Soon Ong

公众号后台回复【m4ml】即可获取这本书。

另外，机器学习的数学基础.pdf