22计算机408考研—数据结构—线性表、栈、队列、数组
2022计算机考研408—数据结构—线性表、栈、队列、数组
手把手教学考研大纲范围内的线性表、栈、队列、数组
22考研大纲数据结构要求的是C/C++,笔者以前使用的都是Java,对于C++还很欠缺,
如有什么建议或者不足欢迎大佬评论区或者私信指出
Talk is cheap. Show me the code.
理论到处都有,代码加例题自己练习才能真的学会
顺序表
官方含义:一段地址连续的存储单元依次存储线性表的数据元素。
其实就相当于数组,`把顺序表当数组看`最简单了
// 顺序表
#include 链表
链表和顺序表其实是差不多的
顺序表在访问下一个的时候是用下标访问
链表访问下一个只能通过结构体中的指针
插入,删除的时候不需要改变其他元素,只需要修改指定元素前后元素的指针即可
//此链表的index为序列号从1开始 !!!!不是下标
//此链表多处用到new ,建议大家删一个new调试一下,就能了解到new和不用new的区别了
#include "iostream"
#include "vector"
using namespace std;
typedef struct LNode {
//LNode类型 包含一个int值和一个指针指向下一个地址
int data;
struct LNode *next;
} LNode, *LinkList;
bool ListInit(LinkList &L, int val) {
//初始化链表,要给一个初始值当作链表头节点
L = new LNode;
L->next = NULL;
L->data = val;
return true;
}
bool ListInsertE(LinkList &L, int val) {
//添加一个元素到链表尾端
LNode *headL = new LNode; //保存一下链表当前的位置
headL = L;
while (L->next) {
//循环到L最后面,然后把当前值给L的下一个
L = L->next;
}
LNode *temp = new LNode; //new一个结点,如果不new可能会使用上一个temp结点
temp->data = val;
temp->next = NULL;
L->next = temp;
L = headL; //链表的头位置给L
}
bool ListInsert(LinkList &L, int index, int val) {
//插入到链表的序列index(注意不是下标)位置
LNode *headL = new LNode; //保存头位置的上一个(headL的下一个是头位置)
headL->next = L; //这里不保存头位置, 防止添加第一个位置时,链表会添加到第二个位置
int j = 0;
while (headL && j < (index - 1)) {
//找到第index个位置
j++;
headL = headL->next;
}
if (!headL || index < 1) {
return false;
}
LNode *temp = new LNode; //new一个结点,(不new可能会用到上一个结点)
temp->data = val;
temp->next = headL->next; //把headL的下一个结点给temp的下一个结点
headL->next = temp; //把temp给headL的下一个结点 现在temp的下一个就是原headL的下一个结点,相当于把temp插入到了里面
L = headL->next;
return true;
}
bool ListDelete(LinkList &L, int index) {
//删除指定序列index的值
LNode *headL = new LNode;
LNode *tempL = new LNode;
tempL->next = L; //tempL的下一个是头节点(防止删除第一个结点出现问题)
headL = tempL; //保存头结点的上一个,就是tempL
int j = 0;
while (tempL && j < (index - 1)) {
//找到序列index的结点
tempL = tempL->next;
j++;
}
if (!tempL) {
//如果tempL为NULL,直接退出,没有要删除的结点
return false;
}
tempL->next = tempL->next->next; //tempL的下一个的下一个给下一个 相当于下一个会被直接盖住(删除了下一个 )
L = headL->next; //把头结点给L
}
bool ListGetElem(LinkList L, int index, int &val) {
//找到知道序列index的值,传送给val
int j = 0;
while (L && j < (index - 1)) {
//找到序列为index的值
L = L->next;
j++;
}
if (!L) {
//如果L为空,直接退出,没有此节点
return false;
}
val = L->data;
return true;
}
int ListGetIndex(LinkList L, int val) {
//通过值找到指定序列下标
int index = 1;
while (L->data != val) {
L = L->next;
index++;
}
if (!L) {
return 0;
}
return index;
}
void ListCreateH(LinkList &L, vector<int> num) {
//前插法创建节点(num数组的值创建链表)
L = new LNode;
L->next = NULL;
for (int i = 0; i < num.size(); i++) {
LNode *p = new LNode;
p->data = num[i];
p->next = L->next; //每次把L的下一个给p的下一个
L->next = p; //然后把p给L的下一个 p的下一个是原来L的下一个
}
L = L->next; //L的下一个才是num数组创建的第一个值
}
void ListCreateE(LinkList &L, vector<int> num) {
//前插法创建节点(num数组的值创建链表)
L = new LNode;
LNode *headL = new LNode;
headL = L;
L->next = NULL;
for (int i = 0; i < num.size(); i++) {
LNode *p = new LNode;
p->data = num[i];
p->next = NULL;
L->next = p; //当前指针p给L的下一个
L = p; //把p给L p的上一个就是原L
}
L = headL->next; //头结点的下一个才是num创建的第一个结点
}
void ListPrint(LinkList L) {
//输出链表各个的值
while (L) {
cout << L->data << " ";
L = L->next;
}
cout << "\n";
}
int main() {
vector<int> num = {
1,2,3,4,5};
LinkList temp;
// ListCreateE(temp, num);
// ListPrint(temp);
// ListCreateH(temp, num);
// ListPrint(temp);
ListInit(temp, 10); //创建List链表
ListInsertE(temp, 10); //尾端插入值
ListInsertE(temp, 10);
ListPrint(temp);
ListInsert(temp, 1, 20); //插入一个值 到序列index位置
ListPrint(temp);
ListDelete(temp, 3); //删除链表中序列index的值
ListPrint(temp);
int val;
ListGetElem(temp, 3, val); //通过序列index找到值,传给val
cout << val << "\n";
ListPrint(temp);
cout << ListGetIndex(temp, 2) << "\n"; //通过值找到序列index
}
双向循环链表
双向循环链表和单链表也是大致相同的
只是在修改结点的关系的时候需要修改每个结点的前后节点
//循环链表
#include "iostream"
#include "vector"
using namespace std;
typedef struct DuLNode {
//结点,每个结点有一个值,
int data; //每个结点包括两个指针,一个指向前一个结点,一个指向后一个结点
struct DuLNode *prior; //指定当前结点的前一个结点
struct DuLNode *next; //指定当前结点的后一个结点
} DuLNode, *DuLinkList;
bool ListInitDul(DuLinkList &L, vector<int> data) {
//初始化双指针循环链表
DuLNode *headL = new DuLNode; //记录一下头结点,初始化结束后,把头结点重新赋值给L
DuLNode *node = new DuLNode; //初始化的时候,把第一个值给node,依次向下连接
node->data = data[0];
L = node;
headL = L;
for (int i = 1; i < data.size(); i++) {
DuLNode *temp = new DuLNode;
temp->data = data[i]; //每次创建一个新的结点,当作node的下一个,绑定与node的关系
node->next = temp; //绑定temp变成node的下一个
temp->prior = node; //绑定node变成temp的上一个
node = temp; //绑定后,把当前点给node, 方便下次循环绑定下一个值
}
node->next = L; //node此时为最后一个值,,node的下一个绑定头结点(循环链表)
L->prior = node; //L的前一个为node,首结点的上一个就是当前链表的最后一个
L = headL; //把初始头结点给L
return true;
}
bool ListGetDulElem(DuLinkList L, int index, DuLNode &node) {
//得到链表序列为index的值,传给node
int j = 1;
while (L && j < index) {
//找到序列为index的结点,
L = L->next; //前面有几个,就循环几次,每次都向下走一位
j++;
}
if (!L) {
//如果L为空,直接跳过
return false;
}
node = *L; //如果不为空,把当前结点传给node
return true;
}
bool ListInsertDul(DuLinkList &L, int index, int data) {
//在序列index位置插入结点
DuLNode *node = new DuLNode;
if (!ListGetDulElem(L, index, *node)) {
//查找一下指定index位置,如果没有当前位置,返回false
return false;
}
//假设在a b的位置插入c(在a b中间插入c,b为node,c为newNode)
//设置c的前一个为a 设置a的下一个为c 设置c的下一个为b 设置b的上一个为c
DuLNode *newNode = new DuLNode;
newNode->data = data;
newNode->prior = node->prior; //把node的前一个给newNode的前一个,
node->prior->next = newNode; //把newNode给node的前一个的后一个
newNode->next = node; //把node给newNode的下一个
node->prior = newNode; //把newNode给node的前一个
if (index == 1) {
//如果是插入第一个的话,返回node的上一个
L = node->prior; //node此时为第二个,新插入的为第一个值,把第一个值给L
}
return true;
}
bool ListDeleteDul(DuLinkList &L, int index) {
//删除序列为index的值
DuLNode *headL = new DuLNode;
headL = L;
DuLNode *node = new DuLNode;
if (!ListGetDulElem(L, index, *node)) {
//找到序列index的结点,传给node
return false;
}
//删除node(node为序列index的结点)
//假设a b c删除 b (b为node)
//设置a的下一个为c 设置c的上一个为a
node->prior->next = node->next;
node->next->prior = node->prior;
return true;
}
void ListPrintDul(DuLinkList L) {
//输出循环节点
if (L == NULL) {
return;
}
DuLNode *headL = new DuLNode; //保存头结点,头结点用来判断是不是已经输出过了
headL = L;
do {
//循环输出
cout << L->data << " ";
L = L->next;
} while (L->next != headL->next); //判断是不是和头结点的下一个相等,如果相等说明已经输出过了
cout << "\n"; //这里有个小bug,如果用L和headL直接比较,相同的结点会显示不同的地址,导致 一直在输出
} //(在线等大佬解决,评论私信指出都可以)
int main() {
DuLinkList LinkList;
vector<int> data = {
1, 2, 3, 4, 5, 6};
ListInitDul(LinkList, data); //把vector传入循环链表
ListInsertDul(LinkList, 1, -1);
ListInsertDul(LinkList, 4, 8);
ListInsertDul(LinkList, 7, 7);
ListInsertDul(LinkList, 2, 4);
ListPrintDul(LinkList);
ListDeleteDul(LinkList, 2); //删除序列号为2的结点
ListPrintDul(LinkList);
DuLNode node;
ListGetDulElem(LinkList, 2, node); //得到序列号index的结点
cout << node.data << "\n";
return 0;
}
栈
和顺序表有点类似
他只能返回栈顶元素,添加栈顶元素
#include "iostream"
using namespace std;
#define MAXSIZE 100 //设置栈的大小
typedef struct {
//栈结构体:栈顶指针,栈底指针,栈的容量
int *base;
int *top;
int stacksize;
}SqStack;
bool InitStack(SqStack &S) {
//初始化栈
S.base = new int[MAXSIZE]; //创建MAXSIZE大小的空间
if (!S.base) {
//如果没创建成功返回false
return false;
}
S.top = S.base; //当前栈没有内容,栈顶和栈底指向一个位置
S.stacksize = MAXSIZE; //栈的容量为MAXSIZE
return true;
}
bool Push(SqStack &S, int data) {
//把data入栈
if (S.top - S.base == S.stacksize) {
//如果栈顶-栈底==栈的容量,证明栈满了,无法添加数据
return false;
}
*S.top++ = data; //top指针位置添加元素,top指向后一个位置
return true;
}
bool Pop(SqStack &S, int &data) {
//出栈,返回值给data
if (S.top == S.base) {
//如果栈顶和栈底指向同一个位置,说明栈内没元素
return false;
}
data = *--S.top; //top指针前移,把值给data
return true;
}
bool Peek(SqStack &S, int &data) {
//peek返回值给data,但栈内不删除
if (S.top != S.base) {
data = *(S.top - 1); //返回top指针前一个位置的值给data
return true;
}
return false;
}
bool StackPrint(SqStack S) {
//输出栈内元素,这里传的不是地址,如果传地址用完还要把指针改到栈顶
while (S.top != S.base) {
//只要栈顶和栈底不是同一个位置,证明栈内元素没有空
cout << *--S.top << " ";
}
cout << "\n";
}
int main() {
SqStack stack;
InitStack(stack); //初始化
Push(stack,10);
Push(stack,30);
Push(stack,20);
Push(stack,50);
StackPrint(stack);
int val;
Pop(stack, val); //出栈
cout << val << " \n";
StackPrint(stack);
Peek(stack, val); //返回栈顶的值,不删除
cout << val << " \n";
StackPrint(stack);
return 0;
}
循环链栈表
栈的链表
栈和链栈的区别就是顺序表和单链表的区别
入栈和出栈只需要改变指定结点的关系
因为栈是单方向的,所以只需要改变单方向结点的关系
#include "iostream"
using namespace std;
typedef struct StackNode{
//链栈结构体:一个数据,一个指向下一位的指针
int data;
struct StackNode *next;
}StackNode, *LinkStack;
bool InitStackNode(LinkStack &L) {
//初始化链栈,直接给链表NULL就可以
L = NULL;
return true;
}
//此压栈方法和单链表的前插法有点类似(如果用后插法,无法访问到上一个结点)
bool Push(LinkStack &L, int data) {
//压入data数据进入链栈
StackNode *temp = new StackNode;
temp->data = data; //给temp数据
temp->next = L; //temp的下一个指向L
L = temp; //temp给L
}
bool Pop(LinkStack &L, int &data) {
//出栈(把数据传给data)
if (L == NULL) {
return false;
}
data = L->data; //传给data,L指向下一个
L = L->next;
return true;
}
bool Peek(LinkStack &L, int &data) {
//返回栈顶元素(给data)
if (L != NULL) {
data = L->data;
return true;
}
return false;
}
void linkStackPrint(LinkStack L) {
//输出链栈
while (L) {
cout << L->data << " ";
L = L->next;
}
cout << "\n";
}
int main() {
LinkStack stack;
InitStackNode(stack); //初始化链栈,插入数据
Push(stack,12);
Push(stack,56);
Push(stack,15);
Push(stack,43);
linkStackPrint(stack);
int val;
Pop(stack, val); //栈顶结点出栈
cout << val << "\n";
linkStackPrint(stack);
Peek(stack, val); //返回栈顶元素(不删除栈顶元素)
cout << val << "\n";
linkStackPrint(stack);
Push(stack,15); //入栈
linkStackPrint(stack);
}
递归斐波那契
递归,其实就是自己不断的调用自己,每次改变参数
第五项的斐波那契 就是第四项+第三项
初始值,第一项,第二项的值为1
第三项的值就是前两个相加
第n项就是(n-1)+(n-2) 不断的调用自己
当找到第1项和第2项的时候直接返回1,我们默认第一项和第二项为1 上面的默认值,我们也称为递归的出口
**递归还有很多变种,(DFS,BFS)在后面的博客中会一一细说的**
#include "iostream"
using namespace std;
int f(int n) {
if (n == 1 || n == 2) {
return 1;
}
return f(n - 1) + f(n - 2);
}
int main() {
cout << f(5);
}
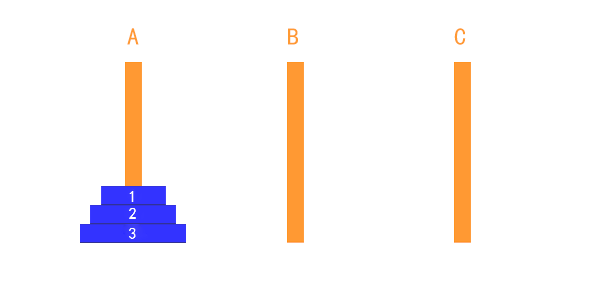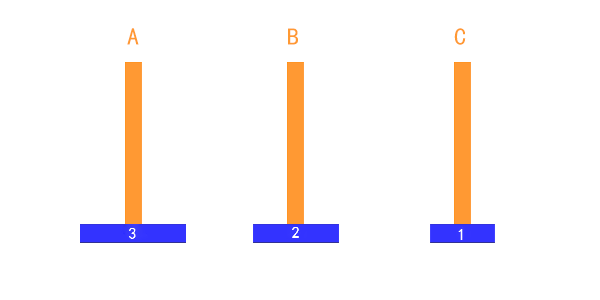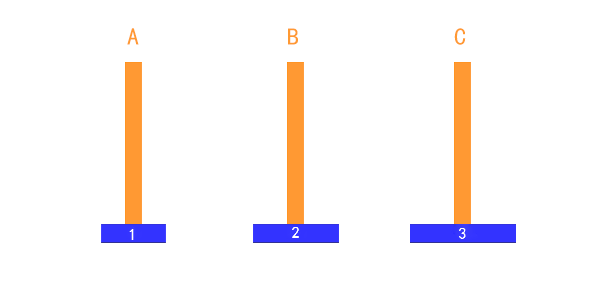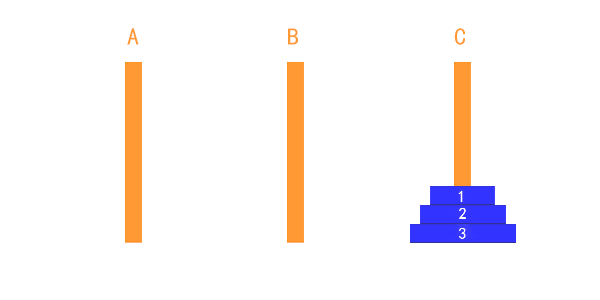
递归汉诺塔
/*
根据汉诺塔的规则:一次只能移动一个托盘,而且必须保证小托盘在大托盘上面,完成A的托盘移动到C
设 1号 为最小的托盘,
用递归思路把这个问题分开,如果想把 n 号托盘移动,需要把 n 号上面的托盘都移动了
然后我们转去移动 n-1 号托盘,一直找到最上面的托盘
当移动 1 号托盘的时候,直接移动到C即可
为什么移动n-1号托盘的时候是传入的Hanoi(n - 1, A, C, B)
Hanoi(n, A, B, C) 是把 n 号托盘从A->C
如果 1号 直接移动到C
那么 2号 的时候就要先移动到B,中转一下,(1号 在C,把 1号 移动到B,空出C来给3号)
3号 移动的时候移动到C,(然后再慢慢把B上的转到C上面(!!!并不是一步从B转到C),把B空出来给下一个托盘)
……一直重复如此
不难发现,1->C,2-B,3->C,4->B……
这就是为什么每次都要C和B换位置的原因,n号移动到B,n-1号就要移动到C
!!!所有的A B C都不是固定的ABC 都和这种类似,临时的ABC
(这么做其实就是确保递归时每次都是从当时方法的目的是A->C 而不是一直要自己变动A->B,A->C 把参数改了,方法不变,就达到一直变动的目的了)
当我们 n-1号 托盘移动完成后(同时意味着 1到(n-1) 都移动完成了),我们就可以把 n号 托盘从A直接转到C上
n号移动以后,把1到(n-1)号托盘从B移动到C,重复上面的操作
如果还是不好理解,多看一看动图理解,或者调试调试代码理解,只看不做很难理解
Talk is Cheap, Show me the Code.
*/
**递归中所有的A B C都不是固定的ABC**
#include "iostream"
using namespace std;
int step = 1;
void Hanoi(int n, char A, char B, char C) {
//将编号为n的托盘从A移动到C,B当作中间托盘
if (n == 1) {
cout << "步数:" << step++ << " 托盘:" << n << " " << A << "->" << C << "\n";
} else {
Hanoi(n - 1, A, C, B); //把(1-(n-1)号托盘)A->B C做中转结点
cout << "步数:" << step++ << " 托盘:" << n << " " << A << "->" << C << "\n";
Hanoi(n - 1, B, A, C); //把(1-(n-1)号托盘)B->C A做中转结点
}
}
int main() {
Hanoi(3,'A','B','C');
return 0;
}
循环队列
循环队列,有点类似双指针数组
左指针存数据后,左指针左移,如果是左端的话,左移到右端
右指针存数据后,右指针右移,如果是右端的话,右移到左端
#include "iostream"
using namespace std;
#define MAXSIZE 10
typedef struct{
//队列结构体:数据,头指针,尾指针
int *num;
int front;
int rear;
}SqQueue;
bool InitQueue(SqQueue &S) {
//初始化队列
S.num = new int[MAXSIZE];
S.front = S.rear = 0; //头指针和尾指针在一块(初始没有数据)
return true;
}
int QueueLength(SqQueue S) {
//返回长度(尾结点-头结点)
return (S.rear - S.front + MAXSIZE) % MAXSIZE;//加上MAXSIZE防止出现负数,有可能出现头结点比尾结点大的情况
}
bool QueueInsertHead(SqQueue &S, int data) {
//队列头结点插入
if ((S.front - 1 + MAXSIZE) % MAXSIZE == S.rear) {
//判断一下是不是满了
return false;
}
S.num[S.front] = data; //插到头结点
//因为他是队列,如果头指针在下标0的地方,那么前移就移动到末尾了
S.front = (S.front - 1 + MAXSIZE) % MAXSIZE; //头指针前移,防止指针-1小于0,
return true;
}
bool QueueInsertEn(SqQueue &S, int data) {
//队列尾结点插入
if ((S.rear + 1) % MAXSIZE == S.front) {
//看是不是满的,尾结点+1可能超过末端,超过末端就从起始端开始算
return false;
}
S.rear = (S.rear + 1) % MAXSIZE; //后移一位
S.num[S.rear] = data; //存放数据
return true;
}
bool QueueDeleteHead(SqQueue &S, int &data) {
//删除头结点,传给data
if (S.front == S.rear) {
//如果是空的没办法传
return false;
}
S.front = (S.front + 1) % MAXSIZE; //头结点后移一位
data = S.num[S.front]; //把值传给data
return true;
}
bool QueueDeleteEn(SqQueue &S, int &data) {
//删除尾结点,传给data
if (S.front == S.rear) {
//判断是否为空
return false;
}
data = S.num[S.rear]; //把值传给data
S.rear = (S.rear - 1 + MAXSIZE) % MAXSIZE; //尾指针前移
return true;
}
bool QueueGetHead(SqQueue &S,int &data) {
//得到头结点
if (S.front == S.rear) {
return false;
}
data = S.num[(S.front + 1) % MAXSIZE];
return true;
}
bool QueueGetEnd(SqQueue &S, int &data) {
//得到尾结点
if (S.front == S.rear) {
return false;
}
data = S.num[S.rear];
return true;
}
bool QueuePrint(SqQueue S) {
//输出队列
while (S.front != S.rear) {
S.front = (S.front + 1) % MAXSIZE;
cout << S.num[S.front] << " ";
int temp = S.num[S.front];
}
cout << "\n";
}
int main() {
SqQueue queue;
InitQueue(queue);
QueueInsertHead(queue, 10);
QueueInsertEn(queue, 40);
QueueInsertHead(queue, 20);
QueueInsertEn(queue, 30);
QueuePrint(queue);
int data;
QueueDeleteEn(queue, data);
cout << "删除尾结点:" << data << "\n";
QueueDeleteHead(queue, data);
cout << "删除头结点:" << data << "\n";
QueueGetHead(queue, data);
cout << "得到头结点:" << data << "\n";
QueueGetEnd(queue, data);
cout << "得到尾结点:" << data << "\n";
cout << "得到长度:" << QueueLength(queue) << "\n";
QueuePrint(queue);
}
链队(链式队列)
每个结点有一个指向下一位的指针
相对双向循环链表简单
#include "iostream"
using namespace std;
typedef struct QNode {
//结点结构体:值,下一位的指针
int data;
struct QNode *next;
} QNode, *QueuePtr;
typedef struct {
//队列包含一个头指针,一个尾指针
QueuePtr front;
QueuePtr rear;
} LinkQueue;
bool InitQueue(LinkQueue &Q) {
//初始化队列
Q.front = Q.rear = new QNode; //创建头尾结点
Q.front->next = NULL; //头结点的下一个为空
Q.front->data = Q.rear->data = NULL; //初始时,头尾结点值为NULL
return true;
}
bool LinkQueueInsertEnd(LinkQueue &Q, int data) {
//添加元素到队尾
if (Q.front == Q.rear && Q.front->data == NULL) {
//如果是第一次进来
Q.rear->data = data; //赋初值
return true;
}
Q.rear->next= new QNode;
Q.rear->next->data = data; //给尾结点的下一个赋值
Q.rear = Q.rear->next; //尾结点指向尾结点的下一个
Q.rear->next = NULL; //尾结点的下一个为空
return true;
}
bool LinkQueueDeleteHead(LinkQueue &Q, int &data) {
//删除头结点
if (Q.front == Q.rear) {
return false;
}
QNode *temp = new QNode;
data = Q.front->data; //保存头结点的值
Q.front = Q.front->next; //头指针指向下一位
}
bool LinkQueueGetHead(LinkQueue &Q, int &data) {
//得到头结点
if (Q.front != Q.rear) {
//队列不为空就返回
data = Q.front->data;
return true;
}
return false;
}
void LinkQueuePrint(LinkQueue Q) {
//输出队列的值
while (Q.front != Q.rear->next) {
cout << Q.front->data << " ";
Q.front = Q.front->next;
}
cout << "\n";
}
int main() {
LinkQueue linkQueue;
InitQueue(linkQueue);
LinkQueueInsertEnd(linkQueue, 10);
LinkQueueInsertEnd(linkQueue, 20);
LinkQueueInsertEnd(linkQueue, 30);
LinkQueueInsertEnd(linkQueue, 40);
LinkQueuePrint(linkQueue);
int val;
LinkQueueDeleteHead(linkQueue, val);
cout << "删除的头结点值为:" << val << "\n";
LinkQueueGetHead(linkQueue, val);
cout << "得到的头结点值为:" << val << "\n";
return 0;
}