2021年五一杯数学建模A题（疫苗生产调度问题）详细分析

目录

一、基本介绍

1.1 题目描述

1.2 待解决问题

二、问题分析与求解

2.1 问题一分析与求解

2.2 问题二分析与求解

2.3 问题三分析与求解

2.4 问题四分析与求解

2.5 问题五分析与求解

 三、总结

---

 

一、基本介绍

1.1 题目描述

新冠肺炎肆虐全球， 给世界带来了深重的灾难。各国为控制疫情纷纷研发新冠疫苗。假定疫苗 生产需要经过 CJ1 工位、 CJ2 工位、 CJ3 工位以及 CJ4 工位等 4 个工艺流程。每个工艺流程一次性 均能处理 100 剂疫苗， 这 100 剂疫苗装进一个加工箱一起送进工位的设备进行处理。而且， 只有按 照 CJ1-CJ2-CJ3-CJ4 的顺序在 4 个工位都进行了加工以后， 才算完成生产。为防止疫苗包装出现混 乱，某疫苗生产公司生产部门规定，每个工位不能同时生产不同类型的疫苗，疫苗生产不允许插队， 即进入第一个工位安排的每类疫苗的生产顺序一旦确定就要一直保持不变， 而且前一种类型的疫苗 离开某个工位后，后一种类型的疫苗才能进入这个工位。

现有 YM1-YM10 等 10 种不同类型的疫苗需要生产。为安全起见，每种类型每箱（内装疫苗 100 剂） 疫苗在每个工位上均进行了 50 次模拟生产。发现， 由于生产设备、疫苗纯化等多种原因， 每个工位生产不同类型的每箱疫苗所需的时间并不稳定，详细的数据见附件 1。

1.2 待解决问题

（1）请对每箱疫苗在所有工位上的生产时间进行均值、方差、最值、概率分布等统计分析，  以方便疫苗生产公司管理者能够直观的掌握每个工位生产疫苗的能力水平，为疫苗生产提供参考。

（2）某国疫苗检测部门紧急需要 YM1-YM10 各 100 剂疫苗进行检测。为赶时间，疫苗生 产公司需要对疫苗的生产顺序进行规划， 以便能在最短时间内交付， 以每个工位生产每箱疫苗平均 时间为依据。请建立数学模型， 制定疫苗生产顺序， 初始时刻为 00:00 ，计算生产总时间，并将结 果填入表 1。

（3）在实际生产中， 每个工位生产每种疫苗的所需时间具有随机性。如果要求该公司疫苗 交货总时间比问题 2 的总时间缩短 5%，请建立数学模型， 以最大的概率完成这个任务为目标， 确定生产顺序， 并给出缩短的时间比例与最大概率之间的关系。

（4）现在该疫苗生产公司接收了 10 种类型疫苗不同规模的生产任务（见附件 2）。由于生  产机器需要检修和维护，每个工位每天生产的时间不能超过 16 小时。为避免疫苗错误包装，要求  每种类型疫苗的生产任务不可以拆分， 即同种类型疫苗生产全部完成之后才能生产另外类型的疫苗。 请建立数学模型，在可靠性为 90%的前提下安排生产方案， 至少多少天可以完成任务？

（5）如果该疫苗生产公司计划在 100 天内选择部分数量的疫苗进行生产，每个工位每天生 产的时间不能超过 16 小时，每种类型疫苗的生产任务可以适当拆分，即每种类型的疫苗可以只完 成一部分。 以最大销售额为目标，请建立数学模型安排生产计划。

二、问题分析与求解

2.1 问题一分析与求解

第一问是从50次时间统计出均值、方差作为正太分布的参数，最值即是公式中的x区间范围。首先对数据进行预处理，再使用MATLAB计算均值、方差、最大值、最小值、峰度和偏度等指标，并使用描述统计、推断统计等方法分析数据特征，设计制作折线图(见图 1)和概率分布直方图，为生产公司管理者提供直观的信息。

正态分布公式如下：

%部分程序如下：
for i = 1:40
    %提取矩阵数据
    YM = x(count:count+4,:);  
    % 求均值，并存入y第一列
    y(i,1) = mean(YM(:));
    % 求方差，并存入y第二列
    y(i,2) = var(YM(:));
    % 求最大值，并存入y第三列
    y(i,3) = max(YM(:));
    % 求最小值，并存入y第四列
    y(i,4) = min(YM(:));
    % 求偏度，并存入y第五列
    y(i,5) = skewness(YM(:));
    % 求峰度，并存入y第六列
    y(i,6) = kurtosis(YM(:));
    % 概率分布，画图
    subplot(4,10,i)  %将图按行列号分布
    histogram(YM(:)) %画直方图
    set(gca,'fontname','宋体','FontSize',14)
    title({['YM',num2str(ceil(i/4)),'-CJ',num2str(mod(i,4))]})
    grid on
    count=count+5;
end

画出各工位的频率分布直方图，可以看出除去某些异常值之后，大致是满足正态分布的，严谨点的话可以画出YM1-YM10各工位的正态分布函数，我会把半成品代码贴在下面~，我当时觉得第一问没必要做这么多，就没弄了，整了个半成品，就注释掉了。

%MATLAB
% for i = 1:40
%     figure
% %     subplot(10,4,i)
%     hold on
%     m=[];
%     m=minzhi(i)-10:0.1:maxzhi(i)+10;
%     n=[];
%     n=exp(-((m-A(i)).^2)./(2*A(i)*A(i)))./(sqrt(2*pi)*S(i));
%     plot(m,n,'b--')
%     m=[];
%     m=minzhi(i):0.1:maxzhi(i);
%     n=[];
%     n=exp(-((m-A(i)).^2)./(2*A(i)*A(i)))./(sqrt(2*pi)*S(i));
%     plot(m,n,'r-')
%     plot([minzhi(i),minzhi(i)],[0,exp(-((minzhi(i)-A(i)).^2)./(2*A(i)*A(i)))./(sqrt(2*pi)*S(i))],'r--')
%     plot([maxzhi(i),maxzhi(i)],[0,exp(-((maxzhi(i)-A(i)).^2)./(2*A(i)*A(i)))./(sqrt(2*pi)*S(i))],'r--')
%     title({['YM',num2str(ceil(i/4)),'—CJ',num2str(mod(i,4)),'正态分布函数：']
%         ['exp(-(x-',num2str(A(i)),'^2)/(2×',num2str(A(i)),'^2))/(sqrt(2*pi)*',num2str(S(i)),')']})
% end

2.2 问题二分析与求解

每种疫苗必须按照CJ1-CJ2-CJ3-CJ4依次加工，题目没有说几条生产线，那么就默认1条，第二问YM1-YM10各100剂已知，疫苗生产也不允许插队，就是说之后的工位也是按第一个工位的加工顺序加工疫苗。那么第二问就直接通过randperm函数生成随机序列就好。加工过程主要有两种增大时间成本的情况：第一种是YM2在CJ1加工完成后YM1还在CJ2上加工，第二种是YM1在CJ2加工完成后，YM2还在CJ1上加工。

造成了等待时间和空挡时间，因此就需要找到一个最优的加工排序方法，在第二问每种疫苗在不同工位的加工时间以附件1中平均时间为依据。
遗传算法流程图如下：

  为了直观，画个甘特图模拟一下各疫苗各工位的生产情况，画的有点丑，没有知乎大神那么牛。

function x=jiaocha(x,n,a)
if nargin < 3
    a=0.3;%未设置交叉率则默认为0.3
end
y=x(end:-1:1);
b=randi(n); %生成随机交叉点
if rand

2.3 问题三分析与求解

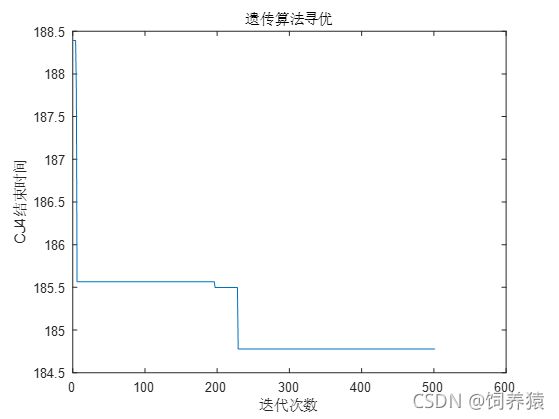
利用所给的50次模拟生产数据，拟合出每种疫苗在各个工位上的正态函数曲线，将生产时间与概率联系在一起，考虑到实际生产过程中各个工位生产每剂疫苗所需时间具有随机性，引入蒙特卡洛模拟方法，结合在第二问的基础上使总时间缩短5%这一约束条件，借助MATLAB软件求解。

%部分程序如下
%遗传算法
Chromosome=600;%染色体数
chrom=[];%生成初始种群
mt=50;%蒙塔卡罗模拟次数
F=[];%储存初始种群时间
TE=[]; %储存
for i=1:Chromosome
    %生成1 到 10 没有重复元素的整数随机排列，作为初始种群
    %未知数为10种疫苗的顺序
    chrom(i,:)=randperm(10);
   
    %由于此处代码与问题二的一部分，为了减少篇幅，将其封装为fitness函数
    for kk=1:mt
        [TE,B]=fitness(A,S,minzhi,maxzhi,chrom(i,:));
        F(i,kk)=TE;%最后CJ4加工结束时刻，单位分钟
        BB{i,kk}=B;
    end
end

%%以当前最优序列算最大概率，蒙塔卡罗模拟100不同缩短时间对应的最大概率
Y=[];
for kk=1:1000
    [G,~,D1,D2]=fitness(A,S,minzhi,maxzhi,bestx);
    %G返回CJ4结束时间，D1返回YM1-YM10在CJ1-CJ4上的加工时间，D2为对应的概率
    Y=[Y;1-G/184.7786,mean(mean(D2))];
end

x=-0.1:0.01:0.1;
js=[];
for i=1:length(x)-1
    js=[js,length(find(Y(find(Y(:,1)>=x(i)),1)

 2.4 问题四分析与求解

该问在问题三模型的基础上增加两个约束条件：完成各种疫苗不同规模的生产任务、每个工位每天生产的时间小于等于 16 小时。此问题中唯一影响总时间的是生产时间的随机性，利用生产时间的概率密度函数，建立所给天数与完成任务可靠性的函数关系式。在可靠性为 90%的前提下安排生产方案，以一天的时间为单位离散化时间，建立差分方程模型，利用Python即可求得结果。

#部分程序
#将附件二要求生产数分成小份，以100剂为一箱
YMnum = [1000, 500, 600, 1000, 1200, 1600, 1800, 800, 600, 900]
YM_ave = YMave_list[0]
YM_std = YMstd_list[0]

CJ_time = [0, 0, 0, 0]
day_count = 0
print(YM_ave)
print(YM_std )

mcm = list()

for k in range(10000):
    #共计生产10000箱疫苗
    T = list()
    T.append(np.random.normal(YMave_list[0][0], YMstd_list[0][0], 1)[0])
    for i in range(1, 4):
        T.append(np.random.normal(YMave_list[0][0], YMstd_list[0][0], 1)[0] + T[i - 1])
    a = Time_Sum(T, YM_ave, YM_std, 1000)

    for i in range(1, 10):
        Time_Sum(T, YMave_list[i], YMstd_list[i], YMnum[i])
    mcm.append(T[3] / 960)

mcm.sort()

2.5 问题五分析与求解

以最大销售额为目标函数重新规划各种疫苗类型的生产量，工位生产时间和公司生产计划天数为约束条件，以各类型疫苗价格和生产数量序列和出厂价格为决策变量，建立单目标组合优化模型。利用遗传算法迭代寻优，可以对任务进行拆分，将任务拆分并编号，同时记录疫苗种类，可以通过randperm产生随机序列，程序中将算目标函数的for循环改为while循环，终止条件为>100天，目标函数改为销售额。

 三、总结

数学建模的趣味就是几乎没有正确答案，解法多种多样，没有绝对的好方法，只要自己用着舒服就OK，上述是我对于这道题的一些粗浅的看法，可能有一些忽略的因素，欢迎各位巨佬指点。

在学习中成功、在学习中进步！我们一起学习不放弃~

记得三连哦~ 你们的支持是我最大的动力！！欢迎大家阅读往期文章哈~

小编联系方式如下，欢迎各位巨佬沟通交流，代码什么的加小编私聊哦~

print("QQ:1654243128")