Pytorch基础教程【阿里云天池—入门】

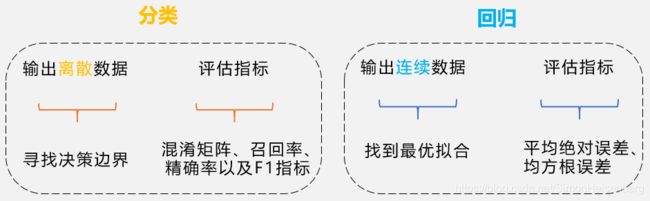
分类、回归基本原理

最常见的监督式学习任务包括回归任务（预测值）和分类任务（预测类）。
在现实生活中，连续值预测问题是非常常见的，比如股价的走势预测、天气预报中温度和湿度等的预测、年龄的预测、交通流量的预测等。对于预测值是连续的实数范围，或者属于某一段连续的实数区间，我们把这种问题称为回归（Regression）问题。特别地，如果使用线性模型去逼近真实模型，那么我们把这一类方法叫做线性回归，线性回归是回归问题中的一种具体的实现。
除了连续值预测问题以外，还有离散值预测问题。比如说硬币正反面的预测，它的预测值y只可能有正面或反面两种可能；再比如说给定一张图片，这张图片中物体的类别也只可能是像猫、狗、天空之类的离散类别值。对于这一类问题，我们把它称为分类（Classification）问题。

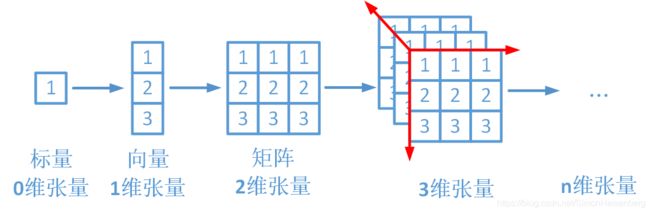
张量的创建

张量（Tensors）类似于NumPy的ndarrays，但张量可以在GPU上进行计算。 所以从本质上来说，PyTorch是一个处理张量的库。一个张量是一个数字、向量、矩阵或任何n维数组。
下面分别展示了0维张量到n位张量：

import torch
import numpy
torch.manual_seed(7) # 固定随机数种子

在深度学习中，我们通常会频繁地对数据进行操作。我们初窥张量，要学会如何去创建、操作张量。建议不要一开始就花费大量时间来研究明白API的作用，可以结合最后的线性回归模型等实战来学习。
张量的创建
张量（Tensors）类似于NumPy的ndarrays（点NumPy实践了解），但张量可以在GPU上进行计算。 所以从本质上来说，PyTorch是一个处理张量的库。一个张量是一个数字、向量、矩阵或任何n维数组。
下面分别展示了0维张量到n位张量： Image
import torch
import numpy
torch.manual_seed(7) # 固定随机数种子
1
import torch
2
import numpy
3
torch.manual_seed(7) # 固定随机数种子

一、直接创建

• torch.tensor(data, dtype=None, device=None, requires_grad=False,
  pin_memory=False)
• 功能：从data创建tensor
• data: 数据，可以是list，numpy
• dtype: 数据类型，默认与data的一致
• device: 所在设备，cuda/cpu requires_grad: 是否需要梯度
• pin_memory: 是否存于锁页内存

torch.tensor([[0.1, 1.2], [2.2, 3.1], [4.9, 5.2]])

• torch.from_numpy(ndarray)
• 功能：从numpy创建tensor
• 注意事项：从torch.from_numpy创建的tensor于原ndarray共享内存，当修改其中一个数据，另一个也将会被改动。

a = numpy.array([1, 2, 3])
t = torch.from_numpy(a)

三、依概率分布创建张量

①

• torch.normal(mean, std, out=None)
• 功能：生成正态分布（高斯分布）
  mean: 均值
  std: 标准差

# mean为张量, std为张量
torch.normal(mean=torch.arange(1., 11.), std=torch.arange(1, 0, -0.1))

②

• torch.normal(mean, std, size, out=None)
• 功能：生成一定大小的生成正态分布（高斯分布）

torch.normal(2, 3, size=(1, 4))

③

• torch.randn(*size, out=None, dtype=None, layout=torch.strided,
  device=None, requires_grad=False)
• 功能：生成标准正态分布
  size: 张量的形状

torch.randn(2, 3)

结果

tensor([[1.3955, 1.3470, 2.4382],
,        [0.2028, 2.4505, 2.0256]])

④

• torch.rand(*size, out=None, dtype=None, layout=torch.strided,
  device=None, requires_grad=False)
• 功能：在区间 [0,1) 上，生成均匀分布

torch.rand(2, 3)

结果

tensor([[0.7405, 0.2529, 0.2332],
,        [0.9314, 0.9575, 0.5575]])

线性回归模型

下面我们开始写一个线性回归模型：

# 首先我们得有训练样本X，Y， 这里我们随机生成
x = torch.rand(20, 1) * 10
y = 2 * x + (5 + torch.randn(20, 1))

# 构建线性回归函数的参数
w = torch.randn((1), requires_grad=True)
b = torch.zeros((1), requires_grad=True)   # 这俩都需要求梯度

# 设置学习率lr为0.1
lr = 0.1

for iteration in range(100):
    # 前向传播
    wx = torch.mul(w, x)
    y_pred = torch.add(wx, b)
 
    # 计算loss
    loss = (0.5 * (y-y_pred)**2).mean()
 
    # 反向传播
    loss.backward()
 
    # 更新参数
    b.data.sub_(lr * b.grad)    # 这种_的加法操作时从自身减，相当于-=
    w.data.sub_(lr * w.grad)

    # 梯度清零
    w.grad.data.zero_()
    b.grad.data.zero_()

print(w.data, b.data)

结果

tensor([-1.0229e+36]) tensor([-1.6542e+35])