CSMA/CD和拥塞控制AIMD其实是一回事!
今天下班的班车上,撸论文,找到一篇关于CSMA/CD性能分析的,然而下载需要钱,作罢。我讨厌知识付费,因为我崇尚知识免费共享。
正好我上周末也写了一篇与此相关的:
谈谈CSMA/CD,TCP中的二进制指数退避算法: https://blog.csdn.net/dog250/article/details/90340322
杭州路况很差,车子里太颠簸,合上电脑,思考即可。
我找到了这里的CSMA/CD的二进制指数退避算法和TCP拥塞控制算法Reno原始版本的AIMD之间的关联,AIMD简直了,就是二进制指数退避的零存整取版本啊。
朋友圈里放话了要今晚作文的,那就作文。很困,还好,迷迷糊糊写完了。
在一群素不相识互不沟通交流的节点中,如何收敛到公平,即 没有中心控制的前提下,如何让所有节点公平共享资源? 这个话题是 统计复用 的分组交换网的精髓中的精髓!不可不察!
分组交换网络的核心技术不是TCP/IP,远远不是,更不是什么HTTP/HTTPS,远远不是,这些充其量叫做工程框架或者再退一步说,它们只是分组交换网的APP。
说起CSMA/CD,大家一定想到的就是以太网。
说起AIMD,大家一定觉得这是在说TCP。
实际上,这两个东西是同一回事,很神奇吧。从一个竟然可以推导出另一个。
不管是CSMA/CD,还是AIMD,其实都是:
- 在一个互不交互资源使用情况的随机系统中,将各个节点收敛到公平的资源利用
就是说, 如果系统中一共有 N 1 , N 2 , . . . N m N_1,N_2,...N_m N1,N2,...Nm这 m m m个节点共享系统的资源 R R R,最终,靠一种非中心控制的机制,让这 m m m个节点每一个节点的资源使用量为 β R m \beta\dfrac{R}{m} βmR,由于仅仅考虑到公平收敛,该机制必然要有所开销,这里的 β \beta β就是开销的系数,它小于1。
这是自组织的。一切都是自动完成的,没有控制中心,没有开始和结束。
我们先从CSMA/CD开始,先看下图:
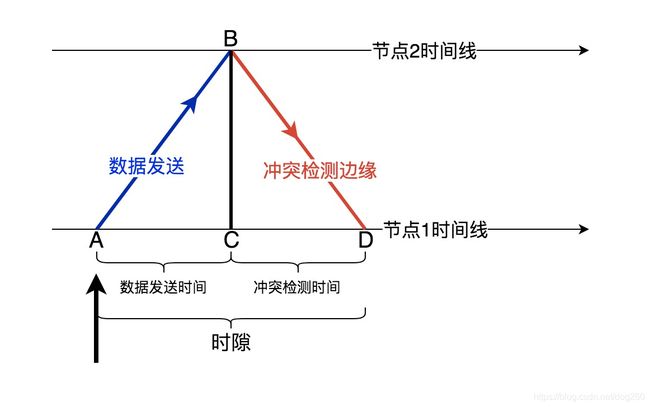
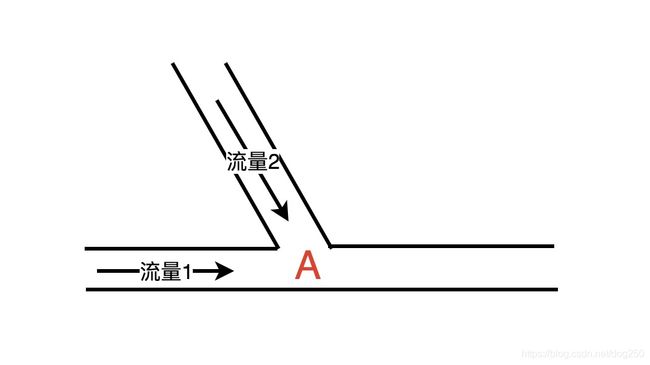
在共享总线介质上,同时只有一个节点可以使用总线。
当节点A在时间点A发送数据包之后,节点2在时间段A~C之间发送数据包的话,就会与节点1的数据包冲突,而冲突导致的碎片信号将会在时间段C~D被节点1和节点2检测到,所以说为了留足冲突检测的时间,一般会采用一个往返时间(即RTT)作为一个 时隙 ,即一个 S l o t Slot Slot 作为数据包占用介质的时间,该 S l o t Slot Slot同时也是数据包重传前等待的基本单位。
换句话说,一个节点发送一个数据包,需要占用一个Slot的时间,如果检测到冲突,该节点在重传数据包前,要等待 k × S l o t k\times Slot k×Slot的时间。
一但某个节点第一次检测到冲突,它 会认为系统中至少还有另一个节点 ,于是,很显然的:
- 整个时间轴要以 2 × S l o t 2\times Slot 2×Slot为单位重新分割为集合 S = { S l o t 0 , S l o t 1 } S=\{Slot_0,Slot_1\} S={ Slot0,Slot1}
检测到冲突的该节点和另一个与之冲突的节点-同时它也能检测到冲突,理想情况下,它们各自占用一个Slot。
那么问题是,谁占用哪个Slot呢?它们之间没有任何协商的机会,在共享介质随机系统中,也不允许它们协商。
最佳答案就是 随机化!
检测到冲突的节点会同时初始化集合 C = { 0 , 1 } C=\{0,1\} C={ 0,1},然后随机在里面挑一个元素作为自己的Slot集合 S S S的下标。最理想的当然是一个节点随机到0,另一个节点随机到1。
然而还会有 50 % 50\% 50%的概率,它们会同时选择0或者同时选择1。这意味着它们会 第二次冲突 ,这时怎么办?
当发生第二次冲突的时候,它们中的任何一个节点均无法区分下面两个情况:
- 既有的两个节点随机到了同一个元素而再次冲突,视为 再冲突 ;
- 新来了1个或者2个或者3个… n n n个新节点和既有的节点冲突,视为 新冲突 ;
即:
- 既有的又检测到二次冲突的节点不知道是老节点还是新节点与之发生了冲突。
为了 收敛到公平 ,系统不能做任何具有偏见的假设,也就是说, 系统要采取的策略,必须针对上述任何一种情况,均适用!
这个策略就是 再次二分退避! 我们看看它的适用性,设既有节点为 2 2 2个:
- 如果和既有节点冲突,再次退避降降低再冲突的概率将减少到 25 % 25\% 25%,收敛;
- 如果和新节点冲突,再次退避将Slot集合 C C C放大到 4 × S l o t 4\times Slot 4×Slot,可容纳最多新增的2个节点,收敛。
那如何应对超过2个的新节点引入的冲突呢?其实不必理会,因为超过2个新节点的话,它们对上述两类情况的影响是等同的。
于是,CSMA/CD的策略可以如下表述。
设一个节点连续检测到 k k k次冲突,那么它重传冲突包前等待的时间将是 r × S l o t r\times Slot r×Slot,其中, r r r是集合 I k = { 0 , 1 , 2 , . . . 2 k − 1 } I_k=\{0,1,2,...2^k-1\} Ik={ 0,1,2,...2k−1}中随机的一个数字。
这个策略天然地具有照顾新来者,惩罚老节点的性质。
如果冲突的概率是均等的,那么老节点连续 k k k次经历冲突后, k k k很大,集合 I k I_k Ik就会很大,如果在该集合随机选择元素的机会是均等的,相比于 k k k比较小的,经历较少冲突的新节点,老节点将有更大的概率等待更久的时间才能重传成功。这个需要解释一下。
一个节点如果持续检测到冲突,假设随机算法是均匀的,那么持续再冲突的概率是很低的,出现这种情况,大概率是遇到了新冲突。CSMA/CD指数退避采用的 本地视角 ,即自己看到了什么,就认为是什么,既然持续冲突被列为是新冲突,则,在 该节点看来 ,就需要为新来的节点开辟Slot,同时 按照无偏见原则,必须退避。
这就是CSMA/CD算法中 二进制指数退避 的全部操作了。如果你理解了这个操作策略,就会发现一个问题。
没有必要非得 × 2 \times 2 ×2啊,也可以检测到冲突后, × 1.5 \times 1.5 ×1.5啊 ,虽然单次再冲突的概率由 50 % 50\% 50%提升到了 75 % 75\% 75%,但随着指数退避,冲突的概率总是会降低趋近于 0 0 0的,这种情况下,CSMA/CD的表述变成了:
设一个节点连续检测到 k k k次冲突,那么它重传冲突包前等待的时间将是 r × S l o t r\times Slot r×Slot,其中, r r r是集合 I k = { 0 , 1 × 1.5 2 , 2 × 1.5 2 , . . . 1. 5 k − 1 } I_k=\{0,\dfrac{1\times 1.5}{2},\dfrac{2\times 1.5}{2},...1.5^k-1\} Ik={ 0,21×1.5,22×1.5,...1.5k−1}中随机的一个数字。
使用 1.5 1.5 1.5替代 2 2 2作为指数退避因子,意味着,用额外 25 % 25\% 25%再冲突的概率而减少 25 % 25\% 25%由于不再冲突而等待的无意义时间。用更小的退避因子,再冲突的概率将会增加,而等待将会减少。更大的退避因子,效果相反。
总结起来,都差不多。场景不同,退避因子的最优解是可选择的。
为什么就是要用 2 2 2而不是 1.5 1.5 1.5或者 2.5 2.5 2.5,我是觉得 2 2 2是最容易计算的,使用别的退避因子将会引入更多的计算指令。
这就是它叫做 二进制指数退避 的原因。
现在看看AIMD。
AIMD其实就是 积累式的指数退避 。
我们先来看一个经典的TCP稳定状态下持续数据传输的图示:
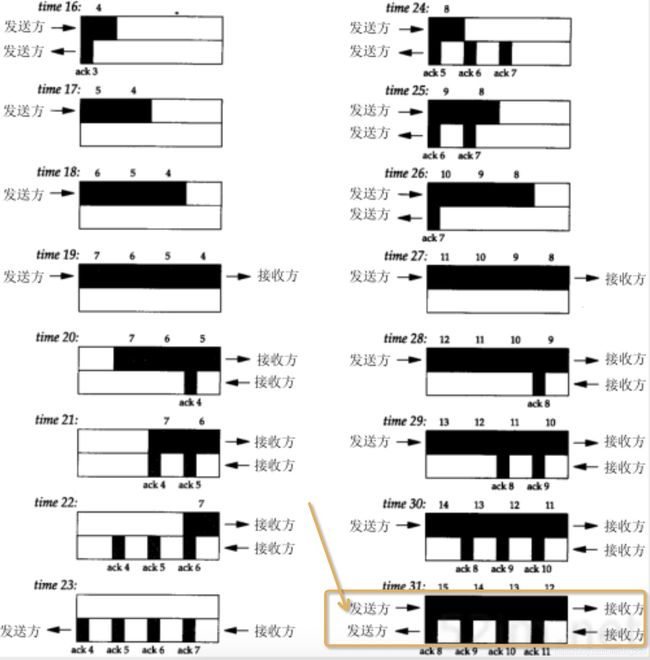
注意最右下角的那个状态,即我们讨论的稳定状态。这是《TCP/IP详解(卷1)》中 “成块数据的吞吐量” 一小节中经典的图。我们假设这是理想情况,数据包按照一定的速率背靠背填满了整个管道。
【注:上面这个图是《TCP/IP详解》的作者史蒂文森的原图,这个和我们理解的TCP不太一样,因为我们被此后的TCP垃圾实现给洗脑了!】
直到BBR算法之前,TCP根本就没有做Pacing,完全是Burst发送的,没有做到流水线,没有做到满载。
TCP的本意是一个RTT发送一个窗口的数据,然而在Pacing之前,几乎这是不可能的!
TCP是垃圾!
在共享介质网络进化到交换式网络后,其它节点的流量将在交换节点插入。现在假设在节点A处,有另外的背靠背流量插入。假设既有的流1的速率是 v 1 v_1 v1,新插入的流2的速率是 v 2 v_2 v2。
如果A这里是早期以太网那样的共享介质网络中的两根 简单绞合在一起的没有智能的线缆 ,那么冲突必然会发生。然而,这里的A点是一个 携带存储器,携带锁存器,携带时钟的智能电路 。
这里是背板!它还有个队列缓存。
和共享介质网络固有的物理机制导致冲突不同的是,交换节点的排队系统只是把冲突延迟了 。并且,虽然是延迟了,但是 账本上还是要记一笔的! 这意味着,冲突的债,迟早要还的!
一旦排队缓存被填满,如果仍有持续到来的两个流的数据包,必然导致数据包被丢掉。
此时,意味着 出现了不可再延迟的冲突 。这里将使用和CSMA/CD的二进制指数退避一模一样的策略。顺便把之前的欠债还掉!
假设缓存的大小为固定值 C C C,介质光速恒定,则缓存中的流1的数据包数量 W 1 W_1 W1和流2的数据包数量 W 2 W_2 W2的比值等于流1和流2的发送速率之比,设流1和流2共同占满排队缓存分别的时间为 T 1 T_1 T1和 T 2 T_2 T2,那么:
C = W 1 + W 2 = v 1 × T 1 + v 2 × T 2 C=W_1+W_2=v_1\times T_1+v_2\times T_2 C=W1+W2=v1×T1+v2×T2
W 1 W 2 = v 1 v 2 \dfrac{W_1}{W_2}=\dfrac{v_1}{v_2} W2W1=v2v1
如果不是因为有这个排队系统,不管是流1还是流2,只要排入一个数据包,就意味着一次冲突, 那么流1积累的冲突数量就是 W 1 W_1 W1,流2积累的冲突数量就是 W 2 W_2 W2,按照二进制指数退避算法,每一次冲突就要将等待时间退避 1 2 \dfrac{1}{2} 21,那么 W 1 W_1 W1次和 W 2 W_2 W2次的冲突将要退避的总时间为:
T W 1 = W 1 × 1 2 T_{W_1}=W_1\times \dfrac{1}{2} TW1=W1×21
T W 2 = W 2 × 1 2 T_{W_2}=W_2\times \dfrac{1}{2} TW2=W2×21
这里计算总冲突量,就是积累式还债。
占据同样的固定不变的缓存 C C C,对于流1,时间增加了 T W 1 T_{W_1} TW1,对于流2,时间增加了 T W 2 T_{W_2} TW2,这意味着它们的速率需要改变。
C = v 1 × T 1 + v 2 × T 2 = v ′ 1 × T W 1 + v ′ 2 × T W 2 = v ′ 1 × 1 2 × W 1 + v ′ 2 × 1 2 × W 2 C=v_1\times T_1+v_2\times T_2=v\prime_1\times T_{W_1}+v\prime_2\times T_{W_2}=v\prime_1\times \dfrac{1}{2}\times W_1+v\prime_2\times \dfrac{1}{2}\times W_2 C=v1×T1+v2×T2=v′1×TW1+v′2×TW2=v′1×21×W1+v′2×21×W2
这意味着流1和流2的速率都要减半。
另一方面,你也可以不从发送速率的视角看这个 减半 操作。如果两个流都保持速率不变,就意味着数据包的包长要减半。
这不就是 MD(乘性减) 的过程吗?
说白了,那就是 MD的过程就是CSMA/CD二进制指数退避的“零存整取”版本!
- 排队是冲突退避零存的过程。
- MD是退避整取的过程。
以上是用 固定速率 的流来映射二进制指数退避的零存整取,获得了一种观感,下面将是正式的映射。
在共享介质的CSMA/CD网络中,有两类退避是被波及的无意义退避:
- 由于随机到同一个Slot而产生再冲突而退避,这是随机数概率问题。
- 由于保守的无偏见原则导致的激进退避,这是为了保证收敛。
如果考虑分布,那么无论上述哪种情况,均是正态分布的两边,离散版本就是泊松分布。随着退避次数的增加,上述两种情况将被消灭。
现在考虑排队系统,假设排队节点可以瞬间操作流1和流2的端到端速率,包大小,而不用类似端到端TCP协议那样等待至少一个RTT,那么谁最后一个发送队列缓存已满,谁将遭遇退避整取的过程。
考虑排队系统的数据到达,这也是一个泊松分布。事实上,填满缓存的最后一个数据包是流1的,还是流2的,这是不确定的,但是统计来看,流1和流2各自占比 50 % 50\% 50%,如果不幸,连续 N N N次均是同一个流遭遇退避整取,即遭遇MD,那么随着 N N N的增加,这种事的概率将会越来越低。
在CSMA/CD中,如果一个节点频繁经历再冲突这种小概率事件,换到积累式的AIMD中,那便是一个流频繁命中队列尾部填充完最后一个位置后到达而被MD惩罚这种小概率事件。都是可以被时间平滑掉的。
于是,MD系统是收敛的。
但是光MD过程还不是公平收敛,这就要扯扯AI了,即加性增的过程。
CSMA/CD中没有AI过程,这是因为CSMA/CD是基于单个数据包停等的,而排队系统依靠 时间墙缓存 将时间流动的范围限制在了带有控制芯片的队列内部,所以消除了信号在裸线上的冲突湮灭,这就使得一个站点背靠背或者按照一定速率持续发送数据包成为了可能。
因此,有了排队系统,单个数据包的停等就没有必要了,此时就是 基于窗口的停等 了。
这就需要引入一个 确认窗口是多少的探测过程 。注意,这个探测过程不是为了收敛,而是为了系统资源的利用率!那么当然要探测到 最大的窗口 方可罢休。
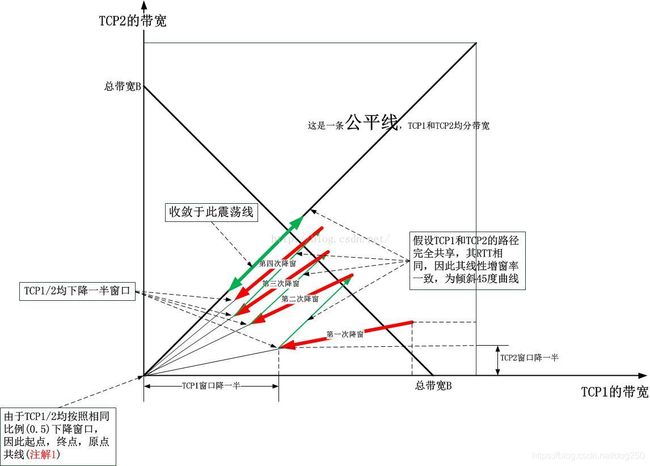
本文不谈这个过程的细节,只说下这个过程就是AI(加性增)的过程,并且按照控制论,只有AIMD才能做到公平收敛,MIMD组合均做不到公平:
- MIMD将会保持二者窗口的比值始终为初始窗口的比。
【画出收敛图,一看便知】
毕竟本文是在聊CSMA/CD与AIMD的关系,CSMA/CD中没有的,本文也就不多说。
如果考虑到AI的影响,那么MD的原因无非也就是两种:
- 由于自己的AI超限导致,自找的。
- 由于新连接介入导致,其它连接导致的收敛。
记住,无论哪一种,只要是排队,就意味着一次 被记账的冲突 ,就意味着 欠了一次退避 ,一旦出现丢包,所有欠下的债,都是要一次性还的!
接下来,我们再来看下CSMA/CD中的两个问题,再看它们在AIMD中的变体。
首先,其指数退避算法中 为什么要用二进制指数退避 ,即为什么要把Slot乘以2。
在CSMA/CD中,使用2作为退避因子的原因是比较容易计算,这个很明确。那么在AIMD中,是否还存在这个约束呢?
由于只是一次性乘性减,那么计算上的繁琐便不存在了!也就是说,如果仅仅是看 是否可以收敛到公平 这一个指标,MD的乘法因子可以随意,不一定非要是 1 2 \dfrac{1}{2} 21,也可以是 3 4 \dfrac{3}{4} 43。
但是,衡量一个AIMD网络综合性能的指标,不仅仅只有收敛,还有带宽利用率,还有丢包率等等。
这些因子之间的具体的数学关系,参考下这篇:
https://www.icir.org/tfrc/aimd.pdf
结论就是, 若要满足网络性能评估体系中的某个指标不变,那么AI增量 a a a以及MD系数 b b b必须遵循一个等量关系。
其次,我们类比下CSMA/CD的发送和AIMD排队系统的数据包到达,二者都遵循泊松分布,二者之间的不同导致了排队系统的效率相比共享介质系统的效率要高太多。
AIMD和CSMA/CD的不同在于,CSMA/CD那是基于概率的事前预测,预测的准确率随着退避而增加最终收敛,然而代价就是但凡是概率系统,总是有误判。
AIMD则是事后记账的系统,只要发生排队事件,那必然是要记账的,这里没有误判,因此便不必付出为误判而消耗的资源。最终,谁排队排得多,在MD过程中乘性减被扣掉的也多,这是一个等比例的无损缩放过程。
比方说,如果两个流在队列中排队的数据包分别为20和40,按照 1 2 \dfrac{1}{2} 21的MD系数,流1将会失去10个数据包的限额,而流2将会失去20个,这是真正的完全公平!
仔细看图,以理解什么是 公平收敛。
再次重申,本文和TCP无关!
分组交换网,一个超级大的范畴,你可以用共享介质实现,运行类似CSMA/CD(CA),你也可以使用排队系统,接入几台路由器交换机。所有的精彩将演绎。
记得在上第二个大学那会儿,第一堂计算机网络课,老师介绍了集线器,交换机的区别,介绍了背板总线带宽…那时的老师就讲过,冲突域受限于背板带宽…如今呢?
问题是,交换机内部的队列缓存中的冲突域到底是什么,这非常复杂,以后分解。
浙江温州皮鞋湿,下雨进水不会胖!