DataWhale集成学习Task2--掌握基本的回归模型
摘要:回顾Task1,分类属于有监督学习的应用之一,其因变量是连续型变量,下面我们来详细解读一下分类,掌握分类的基本模型
机器学习基础
度量指标
- MSE均方误差: MSE ( y , y ^ ) = 1 n samples ∑ i = 0 n samples − 1 ( y i − y ^ i ) 2 . \text{MSE}(y, \hat{y}) = \frac{1}{n_\text{samples}} \sum_{i=0}^{n_\text{samples} - 1} (y_i - \hat{y}_i)^2. MSE(y,y^)=nsamples1∑i=0nsamples−1(yi−y^i)2.
- MAE平均绝对误差: MAE ( y , y ^ ) = 1 n samples ∑ i = 0 n samples − 1 ∣ y i − y ^ i ∣ \text{MAE}(y, \hat{y}) = \frac{1}{n_{\text{samples}}} \sum_{i=0}^{n_{\text{samples}}-1} \left| y_i - \hat{y}_i \right| MAE(y,y^)=nsamples1∑i=0nsamples−1∣yi−y^i∣
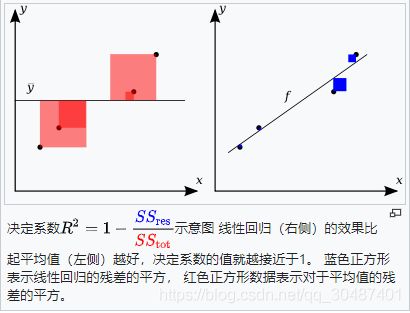
- R 2 R^2 R2决定系数: R 2 ( y , y ^ ) = 1 − ∑ i = 1 n ( y i − y ^ i ) 2 ∑ i = 1 n ( y i − y ˉ ) 2 R^2(y, \hat{y}) = 1 - \frac{\sum_{i=1}^{n} (y_i - \hat{y}_i)^2}{\sum_{i=1}^{n} (y_i - \bar{y})^2} R2(y,y^)=1−∑i=1n(yi−yˉ)2∑i=1n(yi−y^i)2
- 解释方差得分: e x p l a i n e d _ v a r i a n c e ( y , y ^ ) = 1 − V a r { y − y ^ } V a r { y } explained\_{}variance(y, \hat{y}) = 1 - \frac{Var\{ y - \hat{y}\}}{Var\{y\}} explained_variance(y,y^)=1−Var{ y}Var{ y−y^}
模型选择
-
线性回归模型
假设:数据集 D = { ( x 1 , y 1 ) , . . . , ( x N , y N ) } D = \{(x_1,y_1),...,(x_N,y_N) \} D={ (x1,y1),...,(xN,yN)}, x i ∈ R p , y i ∈ R , i = 1 , 2 , . . . , N x_i \in R^p,y_i \in R,i = 1,2,...,N xi∈Rp,yi∈R,i=1,2,...,N, X = ( x 1 , x 2 , . . . , x N ) T , Y = ( y 1 , y 2 , . . . , y N ) T X = (x_1,x_2,...,x_N)^T,Y=(y_1,y_2,...,y_N)^T X=(x1,x2,...,xN)T,Y=(y1,y2,...,yN)T
假设X和Y之间存在线性关系,模型的具体形式为 y ^ = f ( w ) = w T x \hat{y}=f(w) =w^Tx y^=f(w)=wTx最小二乘估计:
我们需要衡量真实值 y i y_i yi与线性回归模型的预测值 w T x i w^Tx_i wTxi之间的差距,在这里我们和使用二范数的平方和L(w)来描述这种差距,即:
L ( w ) = ∑ i = 1 N ∣ ∣ w T x i − y i ∣ ∣ 2 2 = ∑ i = 1 N ( w T x i − y i ) 2 = ( w T X T − Y T ) ( w T X T − Y T ) T = w T X T X w − 2 w T X T Y + Y Y T 因 此 , 我 们 需 要 找 到 使 得 L ( w ) 最 小 时 对 应 的 参 数 w , 即 : w ^ = a r g m i n L ( w ) 为 了 达 到 求 解 最 小 化 L ( w ) 问 题 , 我 们 应 用 高 等 数 学 的 知 识 , 使 用 求 导 来 解 决 这 个 问 题 : ∂ L ( w ) ∂ w = 2 X T X w − 2 X T Y = 0 , 因 此 : w ^ = ( X T X ) − 1 X T Y L(w) = \sum\limits_{i=1}^{N}||w^Tx_i-y_i||_2^2=\sum\limits_{i=1}^{N}(w^Tx_i-y_i)^2 = (w^TX^T-Y^T)(w^TX^T-Y^T)^T = w^TX^TXw - 2w^TX^TY+YY^T\\ 因此,我们需要找到使得L(w)最小时对应的参数w,即:\\ \hat{w} = argmin\;L(w)\\ 为了达到求解最小化L(w)问题,我们应用高等数学的知识,使用求导来解决这个问题: \\ \frac{\partial L(w)}{\partial w} = 2X^TXw-2X^TY = 0,因此: \\ \hat{w} = (X^TX)^{-1}X^TY L(w)=i=1∑N∣∣wTxi−yi∣∣22=i=1∑N(wTxi−yi)2=(wTXT−YT)(wTXT−YT)T=wTXTXw−2wTXTY+YYT因此,我们需要找到使得L(w)最小时对应的参数w,即:w^=argminL(w)为了达到求解最小化L(w)问题,我们应用高等数学的知识,使用求导来解决这个问题:∂w∂L(w)=2XTXw−2XTY=0,因此:w^=(XTX)−1XTY -
线性回归模型推广
为了让线性模型更能表达非线性关系,可以将标准的线性回归模型:
y i = w 0 + w 1 x i + ϵ i y_i = w_0 + w_1x_i + \epsilon_i yi=w0+w1xi+ϵi
换成一个多项式函数:
y i = w 0 + w 1 x i + w 2 x i 2 + . . . + w d x i d + ϵ y_i = w_0 + w_1x_i + w_2x_i^2 + ...+w_dx_i^d + \epsilon yi=w0+w1xi+w2xi2+...+wdxid+ϵ
或者说,使用广义可加模型框架(GAM)
y i = w 0 + ∑ j = 1 p f j ( x i j ) + ϵ i y_i = w_0 + \sum\limits_{j=1}^{p}f_{j}(x_{ij}) + \epsilon_i yi=w0+j=1∑pfj(xij)+ϵi -
回归树
决策树是经典的机器学习算法,很多复杂的机器学习算法都是由决策树演变而来。对于决策树的学习,是我们机器学习课程中非常重要的一个环节。根据处理数据类型的不同,决策树又分为两类:分类决策树与回归决策树。分类决策树可用于处理离散型数据,回归决策树可用于处理连续型数据。
回归树的模型可以表示为: f ( x ) = ∑ m = 1 J c ^ m I ( x ∈ R m ) f(x) = \sum\limits_{m=1}^{J}\hat{c}_mI(x \in R_m) f(x)=m=1∑Jc^mI(x∈Rm)
建立回归树的过程大致可以分为以下两步:
- 将自变量的特征空间(即 x ( 1 ) , x ( 2 ) , x ( 3 ) , . . . , x ( p ) x^{(1)},x^{(2)},x^{(3)},...,x^{(p)} x(1),x(2),x(3),...,x(p))的可能取值构成的集合分割成J个互不重叠的区域 R 1 , R 2 , . . . , R j R_1,R_2,...,R_j R1,R2,...,Rj。
- 对落入区域 R j R_j Rj的每个观测值作相同的预测,预测值等于 R j R_j Rj上训练集的因变量的简单算术平均。
具体来说,就是:
a. 选择最优切分特征j以及该特征上的最优点s:
遍历特征j以及固定j后遍历切分点s,选择使得下式最小的(j,s) m i n j , s [ m i n c 1 ∑ x i ∈ R 1 ( j , s ) ( y i − c 1 ) 2 + m i n c 2 ∑ x i ∈ R 2 ( j , s ) ( y i − c 2 ) 2 ] min_{j,s}[min_{c_1}\sum\limits_{x_i\in R_1(j,s)}(y_i-c_1)^2 + min_{c_2}\sum\limits_{x_i\in R_2(j,s)}(y_i-c_2)^2 ] minj,s[minc1xi∈R1(j,s)∑(yi−c1)2+minc2xi∈R2(j,s)∑(yi−c2)2]
b. 按照(j,s)分裂特征空间: R 1 ( j , s ) = { x ∣ x j ≤ s } 和 R 2 ( j , s ) = { x ∣ x j > s } , c ^ m = 1 N m ∑ x ∈ R m ( j , s ) y i , m = 1 , 2 R_1(j,s) = \{x|x^{j} \le s \}和R_2(j,s) = \{x|x^{j} > s \},\hat{c}_m = \frac{1}{N_m}\sum\limits_{x \in R_m(j,s)}y_i,\;m=1,2 R1(j,s)={ x∣xj≤s}和R2(j,s)={ x∣xj>s},c^m=Nm1x∈Rm(j,s)∑yi,m=1,2
c. 继续调用步骤1,2直到满足停止条件,就是每个区域的样本数小于等于5。
d. 将特征空间划分为J个不同的区域,生成回归树: f ( x ) = ∑ m = 1 J c ^ m I ( x ∈ R m ) f(x) = \sum\limits_{m=1}^{J}\hat{c}_mI(x \in R_m) f(x)=m=1∑Jc^mI(x∈Rm)
如下图是一棵完整的回归树:

-
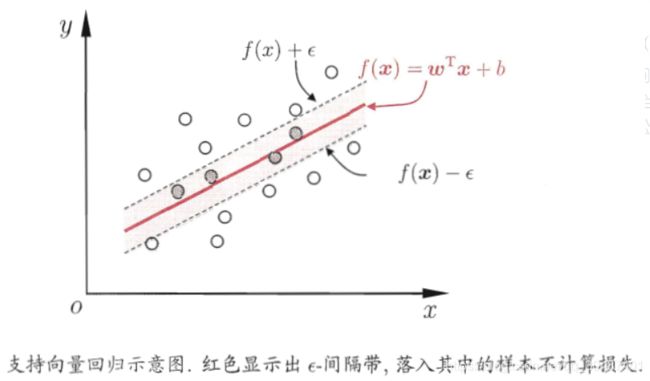
在线性回归的理论中,每个样本点都要计算平方损失,但是SVR却是不一样的。SVR认为:落在 f ( x ) f(x) f(x)的 ϵ \epsilon ϵ邻域空间中的样本点不需要计算损失,这些都是预测正确的,其余的落在 ϵ \epsilon ϵ邻域空间以外的样本才需要计算损失,因此:
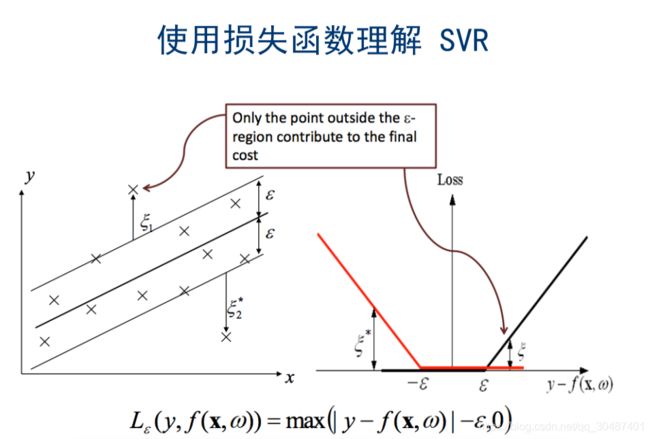
m i n w , b , ξ i , ξ ^ i 1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ i = 1 N ( ξ i , ξ ^ i ) s . t . f ( x i ) − y i ≤ ϵ + ξ i y i − f ( x i ) ≤ ϵ + ξ ^ i ξ i , ξ ^ i ≤ 0 , i = 1 , 2 , . . . , N min_{w,b,\xi_i,\hat{\xi}_i} \frac{1}{2}||w||^2 +C \sum\limits_{i=1}^{N}(\xi_i,\hat{\xi}_i)\\ s.t.\;\;\; f(x_i) - y_i \le \epsilon + \xi_i\\ \;\;\;\;\;y_i - f(x_i) \le \epsilon +\hat{\xi}_i\\ \;\;\;\;\; \xi_i,\hat{\xi}_i \le 0,i = 1,2,...,N minw,b,ξi,ξ^i21∣∣w∣∣2+Ci=1∑N(ξi,ξ^i)s.t.f(xi)−yi≤ϵ+ξiyi−f(xi)≤ϵ+ξ^iξi,ξ^i≤0,i=1,2,...,N
引入拉格朗日函数:
L ( w , b , α , α ^ , ξ , ξ , μ , μ ^ ) = 1 2 ∥ w ∥ 2 + C ∑ i = 1 N ( ξ i + ξ ^ i ) − ∑ i = 1 N ξ i μ i − ∑ i = 1 N ξ ^ i μ ^ i + ∑ i = 1 N α i ( f ( x i ) − y i − ϵ − ξ i ) + ∑ i = 1 N α ^ i ( y i − f ( x i ) − ϵ − ξ ^ i ) \begin{array}{l} L(w, b, \alpha, \hat{\alpha}, \xi, \xi, \mu, \hat{\mu}) \\ \quad=\frac{1}{2}\|w\|^{2}+C \sum_{i=1}^{N}\left(\xi_{i}+\widehat{\xi}_{i}\right)-\sum_{i=1}^{N} \xi_{i} \mu_{i}-\sum_{i=1}^{N} \widehat{\xi}_{i} \widehat{\mu}_{i} \\ \quad+\sum_{i=1}^{N} \alpha_{i}\left(f\left(x_{i}\right)-y_{i}-\epsilon-\xi_{i}\right)+\sum_{i=1}^{N} \widehat{\alpha}_{i}\left(y_{i}-f\left(x_{i}\right)-\epsilon-\widehat{\xi}_{i}\right) \end{array} L(w,b,α,α^,ξ,ξ,μ,μ^)=21∥w∥2+C∑i=1N(ξi+ξ i)−∑i=1Nξiμi−∑i=1Nξ iμ i+∑i=1Nαi(f(xi)−yi−ϵ−ξi)+∑i=1Nα i(yi−f(xi)−ϵ−ξ i)
再令 L ( w , b , α , α ^ , ξ , ξ , μ , μ ^ ) L(w, b, \alpha, \hat{\alpha}, \xi, \xi, \mu, \hat{\mu}) L(w,b,α,α^,ξ,ξ,μ,μ^)对 w , b , ξ , ξ ^ w,b,\xi,\hat{\xi} w,b,ξ,ξ^求偏导等于0,得: w = ∑ i = 1 N ( α ^ i − α i ) x i w=\sum_{i=1}^{N}\left(\widehat{\alpha}_{i}-\alpha_{i}\right) x_{i} w=∑i=1N(α i−αi)xi。
上述过程中需满足KKT条件,即要求:
{ α i ( f ( x i ) − y i − ϵ − ξ i ) = 0 α i ^ ( y i − f ( x i ) − ϵ − ξ ^ i ) = 0 α i α ^ i = 0 , ξ i ξ ^ i = 0 ( C − α i ) ξ i = 0 , ( C − α ^ i ) ξ ^ i = 0 \left\{\begin{array}{c} \alpha_{i}\left(f\left(x_{i}\right)-y_{i}-\epsilon-\xi_{i}\right)=0 \\ \hat{\alpha_{i}}\left(y_{i}-f\left(x_{i}\right)-\epsilon-\hat{\xi}_{i}\right)=0 \\ \alpha_{i} \widehat{\alpha}_{i}=0, \xi_{i} \hat{\xi}_{i}=0 \\ \left(C-\alpha_{i}\right) \xi_{i}=0,\left(C-\widehat{\alpha}_{i}\right) \hat{\xi}_{i}=0 \end{array}\right. ⎩⎪⎪⎪⎨⎪⎪⎪⎧αi(f(xi)−yi−ϵ−ξi)=0αi^(yi−f(xi)−ϵ−ξ^i)=0αiα i=0,ξiξ^i=0(C−αi)ξi=0,(C−α i)ξ^i=0
SVR的解形如: f ( x ) = ∑ i = 1 N ( α ^ i − α i ) x i T x + b f(x)=\sum_{i=1}^{N}\left(\widehat{\alpha}_{i}-\alpha_{i}\right) x_{i}^{T} x+b f(x)=∑i=1N(α i−αi)xiTx+b
使用sklearn构建完整的回归项目
一般来说,一个完整的机器学习项目分为以下步骤:
- 明确项目任务:回归/分类
- 收集数据集并选择合适的特征。
- 选择度量模型性能的指标。
- 选择具体的模型并进行训练以优化模型。
- 评估模型的性能并调参。
收集数据集并选择合适特征
在数据集上直接采用上一个任务中用到的波士顿房价数据集
# 引入相关科学计算包
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
plt.style.use("ggplot")
import seaborn as sns
from sklearn import datasets
boston = datasets.load_boston() # 返回一个类似于字典的类
X = boston.data
y = boston.target
features = boston.feature_names
boston_data = pd.DataFrame(X,columns=features)
boston_data["Price"] = y
boston_data.head()
| CRIM | ZN | INDUS | CHAS | NOX | RM | AGE | DIS | RAD | TAX | PTRATIO | B | LSTAT | Price | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.00632 | 18.0 | 2.31 | 0.0 | 0.538 | 6.575 | 65.2 | 4.0900 | 1.0 | 296.0 | 15.3 | 396.90 | 4.98 | 24.0 |
| 1 | 0.02731 | 0.0 | 7.07 | 0.0 | 0.469 | 6.421 | 78.9 | 4.9671 | 2.0 | 242.0 | 17.8 | 396.90 | 9.14 | 21.6 |
| 2 | 0.02729 | 0.0 | 7.07 | 0.0 | 0.469 | 7.185 | 61.1 | 4.9671 | 2.0 | 242.0 | 17.8 | 392.83 | 4.03 | 34.7 |
| 3 | 0.03237 | 0.0 | 2.18 | 0.0 | 0.458 | 6.998 | 45.8 | 6.0622 | 3.0 | 222.0 | 18.7 | 394.63 | 2.94 | 33.4 |
| 4 | 0.06905 | 0.0 | 2.18 | 0.0 | 0.458 | 7.147 | 54.2 | 6.0622 | 3.0 | 222.0 | 18.7 | 396.90 | 5.33 | 36.2 |
各个特征的相关解释:
- CRIM:各城镇的人均犯罪率
- ZN:规划地段超过25,000平方英尺的住宅用地比例
- INDUS:城镇非零售商业用地比例
- CHAS:是否在查尔斯河边(=1是)
- NOX:一氧化氮浓度(/千万分之一)
- RM:每个住宅的平均房间数
- AGE:1940年以前建造的自住房屋的比例
- DIS:到波士顿五个就业中心的加权距离
- RAD:放射状公路的可达性指数
- TAX:全部价值的房产税率(每1万美元)
- PTRATIO:按城镇分配的学生与教师比例
- B:1000(Bk - 0.63)^2其中Bk是每个城镇的黑人比例
- LSTAT:较低地位人口
- Price:房价
选择度量模型性能的指标
在这个案例中,我们使用MSE均方误差为模型的性能度量指标。
选择具体的模型
-
线性回归模型
https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html#sklearn.linear_model.LinearRegression
- 属性:
coef_: 形状为(n_features,)或(n_targets,n_features)的数组
线性回归问题的估计系数。如果在拟合过程中传递了多个目标(y 2D),则这是一个2D形状的数组(n_targets,n_features),而如果仅传递了一个目标,则这是长度为n_features的一维数组。
- 方法:
score(X,y,sample_weight = None)
返回确定系数 R 2 R^2 R2预测的。
R 2 R^2 R2决定系数: R 2 ( y , y ^ ) = 1 − ∑ i = 1 n ( y i − y ^ i ) 2 ∑ i = 1 n ( y i − y ˉ ) 2 R^2(y, \hat{y}) = 1 - \frac{\sum_{i=1}^{n} (y_i - \hat{y}_i)^2}{\sum_{i=1}^{n} (y_i - \bar{y})^2} R2(y,y^)=1−∑i=1n(yi−yˉ)2∑i=1n(yi−y^i)2
from sklearn import linear_model # 引入线性回归方法
lin_reg = linear_model.LinearRegression() # 创建线性回归的类
lin_reg.fit(X,y) # 输入特征X和因变量y进行训练
print("模型系数:",lin_reg.coef_) # 输出模型的系数
print("模型得分:",lin_reg.score(X,y)) # 输出模型的决定系数R^2
模型系数: [-1.08011358e-01 4.64204584e-02 2.05586264e-02 2.68673382e+00
-1.77666112e+01 3.80986521e+00 6.92224640e-04 -1.47556685e+00
3.06049479e-01 -1.23345939e-02 -9.52747232e-01 9.31168327e-03
-5.24758378e-01]
模型得分: 0.7406426641094095
-
线性回归模型推广
(a)多项式回归:
https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.PolynomialFeatures.html?highlight=poly#sklearn.preprocessing.PolynomialFeatures
- 参数:
degree:特征转换的阶数。
interaction_onlyboolean:是否只包含交互项,默认False 。
include_bias:是否包含截距项,默认True。
order:str in {‘C’, ‘F’}, default ‘C’,输出数组的顺序。
from sklearn.preprocessing import PolynomialFeatures
X_arr = np.arange(6).reshape(3,2)
print("原始X为: \n",X_arr)
poly = PolynomialFeatures(2)
print("2次转化X:\n",poly.fit_transform(X_arr)) # 生成多项式和交互特征
ploy = PolynomialFeatures(interaction_only=True)
print("2次转化X:\n",poly.fit_transform(X_arr))
原始X为:
[[0 1]
[2 3]
[4 5]]
2次转化X:
[[ 1. 0. 1. 0. 0. 1.]
[ 1. 2. 3. 4. 6. 9.]
[ 1. 4. 5. 16. 20. 25.]]
2次转化X:
[[ 1. 0. 1. 0. 0. 1.]
[ 1. 2. 3. 4. 6. 9.]
[ 1. 4. 5. 16. 20. 25.]]
(b)GAM模型
https://github.com/dswah/pyGAM/blob/master/doc/source/notebooks/quick_start.ipynb
from pygam import LinearGAM
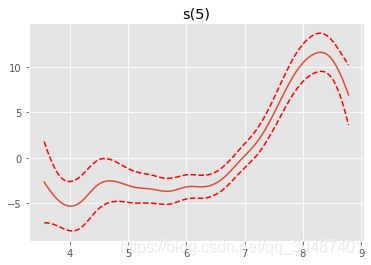
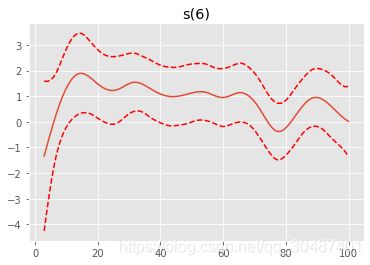
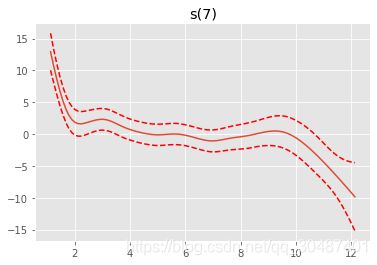
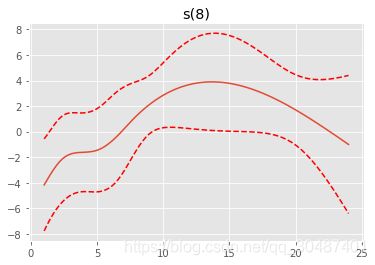
gam = LinearGAM().fit(boston_data[boston.feature_names], y)
gam.summary()
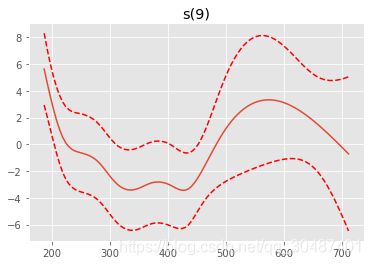
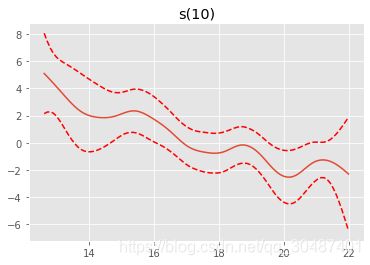
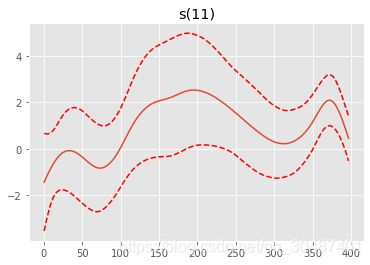
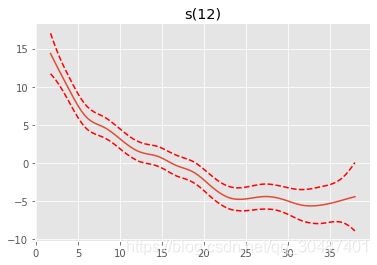
for i, term in enumerate(gam.terms):
if term.isintercept:
continue
XX = gam.generate_X_grid(term=i)
pdep, confi = gam.partial_dependence(term=i, X=XX, width=0.95)
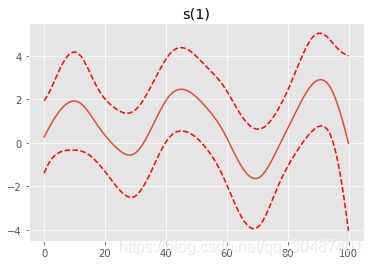
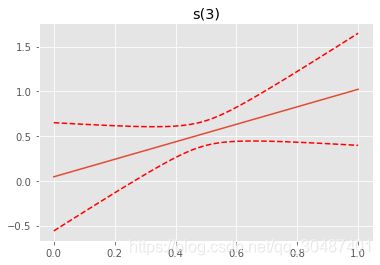
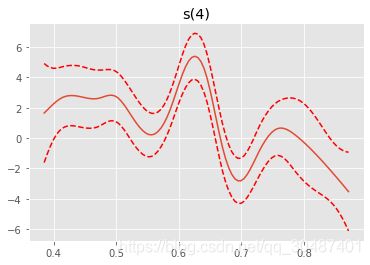
plt.figure()
plt.plot(XX[:, term.feature], pdep)
plt.plot(XX[:, term.feature], confi, c='r', ls='--')
plt.title(repr(term))
plt.show()
LinearGAM
=============================================== ==========================================================
Distribution: NormalDist Effective DoF: 103.2423
Link Function: IdentityLink Log Likelihood: -1589.7653
Number of Samples: 506 AIC: 3388.0152
AICc: 3442.7649
GCV: 13.7683
Scale: 8.8269
Pseudo R-Squared: 0.9168
==========================================================================================================
Feature Function Lambda Rank EDoF P > x Sig. Code
================================= ==================== ============ ============ ============ ============
s(0) [0.6] 20 11.1 2.20e-11 ***
s(1) [0.6] 20 12.8 8.15e-02 .
s(2) [0.6] 20 13.5 2.59e-03 **
s(3) [0.6] 20 3.8 2.76e-01
s(4) [0.6] 20 11.4 1.11e-16 ***
s(5) [0.6] 20 10.1 1.11e-16 ***
s(6) [0.6] 20 10.4 8.22e-01
s(7) [0.6] 20 8.5 4.44e-16 ***
s(8) [0.6] 20 3.5 5.96e-03 **
s(9) [0.6] 20 3.4 1.33e-09 ***
s(10) [0.6] 20 1.8 3.26e-03 **
s(11) [0.6] 20 6.4 6.25e-02 .
s(12) [0.6] 20 6.5 1.11e-16 ***
intercept 1 0.0 2.23e-13 ***
==========================================================================================================
Significance codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
WARNING: Fitting splines and a linear function to a feature introduces a model identifiability problem
which can cause p-values to appear significant when they are not.
WARNING: p-values calculated in this manner behave correctly for un-penalized models or models with
known smoothing parameters, but when smoothing parameters have been estimated, the p-values
are typically lower than they should be, meaning that the tests reject the null too readily.
D:\Anaconda3\envs\dl\lib\site-packages\ipykernel_launcher.py:3: UserWarning: KNOWN BUG: p-values computed in this summary are likely much smaller than they should be.
Please do not make inferences based on these values!
Collaborate on a solution, and stay up to date at:
github.com/dswah/pyGAM/issues/163
This is separate from the ipykernel package so we can avoid doing imports until
-
回归树
https://scikit-learn.org/stable/modules/generated/sklearn.tree.DecisionTreeRegressor.html?highlight=tree#sklearn.tree.DecisionTreeRegressor
- 参数:(列举几个重要的,常用的,详情请看上面的官网)
criterion:{“ mse”,“ friedman_mse”,“ mae”},默认=“ mse”。衡量分割标准的函数 。
splitter:{“best”, “random”}, default=”best”。分割方式。
max_depth:树的最大深度。
min_samples_split:拆分内部节点所需的最少样本数,默认是2。
min_samples_leaf:在叶节点处需要的最小样本数。默认是1。
min_weight_fraction_leaf:在所有叶节点处(所有输入样本)的权重总和中的最小加权分数。如果未提供sample_weight,则样本的权重相等。默认是0
from sklearn.tree import DecisionTreeRegressor
reg_tree = DecisionTreeRegressor(criterion = "mse",min_samples_leaf = 5)
reg_tree.fit(X,y)
reg_tree.score(X,y)
0.9376307599929274
-
支持向量机回归(SVR)
https://scikit-learn.org/stable/modules/generated/sklearn.svm.SVR.html?highlight=svr#sklearn.svm.SVR
- 参数:
kernel:核函数,{‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’}, 默认=’rbf’。
degree:多项式核函数的阶数。默认 = 3。
C:正则化参数,默认=1.0。(后面会详细介绍)
epsilon:SVR模型允许的不计算误差的邻域大小。默认0.1。
from sklearn.svm import SVR
from sklearn.preprocessing import StandardScaler # 标准化数据
from sklearn.pipeline import make_pipeline # 使用管道,把预处理和模型形成一个流程
reg_svr = make_pipeline(StandardScaler(), SVR(C=1.0, epsilon=0.2))
reg_svr.fit(X, y)
reg_svr.score(X,y)
0.7024525421955277