DataWhale集成学习Task5--掌握基本的分类模型
文章目录
- 总览
- 收集数据集并选择合适的特征
- 选择度量模型性能的指标
- 选择具体的模型并进行训练
-
- 逻辑回归
- 基于概率的分类模型:
-
- 线性判别分析
-
- 基于贝叶斯公式对线性判别分析的理解
- 降维分类的思想理解线性判别分析
- 朴素贝叶斯
- 决策树
- 支持向量机SVM
-
- 推导过程
- 非线性支持向量机
- 小结
摘要:从Task5开始,我们就开始学习新的模型,有监督学习的另一大类,分类模型。其最大的特点为因变量是离散型变量
总览
一般来说,一个完整的分类项目分为以下步骤:
- 收集数据集并选择合适的特征
- 选择度量模型性能的指标
- 选择具体的模型并进行训练
收集数据集并选择合适的特征
在数据集上我们使用task1就用到的IRIS鸢尾花数据集。
import pandas as pd
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data
y = iris.target
feature = iris.feature_names
data = pd.DataFrame(X,columns=feature)
data['target'] = y
data.head()
| sepal length (cm) | sepal width (cm) | petal length (cm) | petal width (cm) | target | |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | 0 |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | 0 |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | 0 |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | 0 |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | 0 |
选择度量模型性能的指标
分类模型的度量性能指标与回归任务的有很大差异,原因在于,首先分类问题本身因变量是离散变量,不可能像回归问题那样,根据预测值和因变量的相似度来衡量。其次,,在分类任务中,我们对于每个类别犯错的代价不尽相同
对此,我们引入了混淆矩阵(Confuse Matrix),它是一个2 × 2的情形分析表,显示以下四组记录的数目:
- 作出正确判断的肯定记录(真阳性)
- 作出错误判断的肯定记录(假阴性)
- 作出正确判断的否定记录(真阴性)
- 作出错误判断的否定记录(假阳性)。
如下图所示
那么我们可以得到一系列的评价指标:
- 准确率:分类正确的样本数占总样本的比例,即: A C C = T P + T N F P + F N + T P + T N ACC = \frac{TP+TN}{FP+FN+TP+TN} ACC=FP+FN+TP+TNTP+TN.
- 精度:预测为正且分类正确的样本占预测值为正的比例,即: P R E = T P T P + F P PRE = \frac{TP}{TP+FP} PRE=TP+FPTP.
- 召回率:预测为正且分类正确的样本占类别为正的比例,即: R E C = T P T P + F N REC = \frac{TP}{TP+FN} REC=TP+FNTP.
- F1值:综合衡量精度和召回率,即: F 1 = 2 P R E × R E C P R E + R E C F1 = 2\frac{PRE\times REC}{PRE + REC} F1=2PRE+RECPRE×REC.
- ROC曲线:以假阳率为横轴,真阳率为纵轴画出来的曲线,曲线下方面积越大越好。
在本案例中,用ROC曲线作为最终评价指标。
选择具体的模型并进行训练
逻辑回归
一般来说,逻辑回归是用来解决二分类(0 or 1)问题的,如果分类变量是多类的时候,就不太可用了.
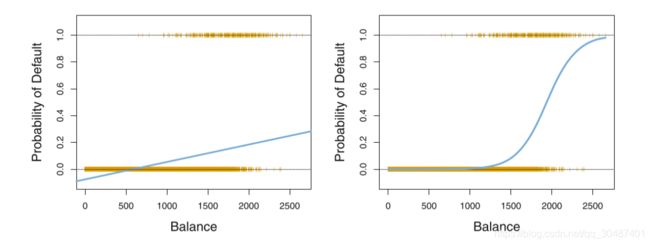
logistic 函数: p ( X ) = e β 0 + β 1 X 1 + e β 0 + β 1 X {p(X) = \dfrac{e^{\beta_0 + \beta_1X}}{1+e^{\beta_0 + \beta_1X}}} p(X)=1+eβ0+β1Xeβ0+β1X (图像如下图所示,左边是线性回归,右边是逻辑函数)
logistic 函数的作用:将是实数轴上的数转换为[0:1]区间上的概率
逻辑回归和线性回归的区别:
逻辑回归(Logistic Regression)与线性回归(Linear Regression)都是一种广义线性模型(generalized linear model)。逻辑回归假设因变量 y 服从伯努利分布,而线性回归假设因变量 y 服从高斯分布。
# 逻辑回归
'''
penalty {‘l1’, ‘l2’, ‘elasticnet’, ‘none’}, default=’l2’正则化方式
dual bool, default=False 是否使用对偶形式,当n_samples> n_features时,默认dual = False。
C float, default=1.0
solver {‘newton-cg’, ‘lbfgs’, ‘liblinear’, ‘sag’, ‘saga’}, default=’lbfgs’
l1_ratio float, default=None
'''
from sklearn.linear_model import LogisticRegression
log_iris = LogisticRegression()
log_iris.fit(X,y)
log_iris.score(X,y)
0.9733333333333334
基于概率的分类模型:
线性判别分析
可以通过基于贝叶斯公式和降维分类的思想去理解
基于贝叶斯公式对线性判别分析的理解
贝叶斯定理: P ( Y = k ∣ X = x ) = π k f k ( x ) ∑ l = 1 K π l f l ( x ) {P(Y=k|X=x) = \dfrac{ {\pi}_kf_k(x)}{\sum\limits_{l=1}^K{\pi}_lf_l(x)}} P(Y=k∣X=x)=l=1∑Kπlfl(x)πkfk(x)
它给出了给定样本的条件下,Y=k这个类别下的概率,这给分类问题提供了一条思路,那就是计算这个 P ( Y = k ∣ X = x ) {P(Y=k|X=x)} P(Y=k∣X=x),而且我们的逻辑回归就是这么干的
但是在 P ( Y = k ∣ X = x ) = π k f k ( x ) ∑ l = 1 K π l f l ( x ) {P(Y=k|X=x) = \dfrac{ {\pi}_kf_k(x)}{\sum\limits_{l=1}^K{\pi}_lf_l(x)}} P(Y=k∣X=x)=l=1∑Kπlfl(x)πkfk(x)这个公式中,分母 ∑ l = 1 K π l f l ( x ) = P ( X = x ) { {\sum\limits_{l=1}^K{\pi}_lf_l(x)} = P(X=x)} l=1∑Kπlfl(x)=P(X=x)当样本给定的时候是一个与分类 k {k} k无关的常数,所以我们的问题可以简化为只需要计算分子 π k f k ( x ) { {\pi}_kf_k(x)} πkfk(x),进而比较哪个类别的概率最大就知道属于哪个类别了,因此我们的分类思路就出来啦,这个思路不同于逻辑回归,逻辑回归需要计算具体的 P ( Y = k ∣ X = x ) {P(Y=k|X=x)} P(Y=k∣X=x)概率值,而我们现在的思路是通过贝叶斯定理计算贝叶斯定理的分子,比较分子最大的那个类别为最终类别。
降维分类的思想理解线性判别分析
基于数据进行分类时,一个很自然的想法是:将高维的数据降维至一维,然后使用某个阈值将各个类别分开。下面用图的形式展示:
图中,数据的维度是二维的,我们的想法是把数据降维至一维,然后用阈值就能分类。这个似乎是一个很好的想法,我们总是希望降维后的数据同一个类别自身内部方差小,不同类别之间的方差要尽可能大。这也是合理的,因为同一个类别的数据应该更加相似,因此方差小;不同类别的数据之间应该很不相似,这样才能更容易对数据进行分类,我们简称为:类内方差小,类间方差大,在计算机语言叫“松耦合,高内聚”。
推导过程:
在做具体的推导之前,我们对数据的形式和一些基本统计量做一些描述:
特征 X = ( x 1 , x 2 , . . . , x N ) T X = (x_1,x_2,...,x_N)^T X=(x1,x2,...,xN)T,因变量 Y = ( y 1 , y 2 , . . . , y N ) T , 其 中 , y i ∈ { + 1 , − 1 } Y = (y_1,y_2,...,y_N)^T,\;\;其中,y_i \in \{+1,-1 \} Y=(y1,y2,...,yN)T,其中,yi∈{ +1,−1},类别c1的特征 X c 1 = { x i ∣ y i = + 1 } X_{c_1} = \{x_i|y_i=+1 \} Xc1={ xi∣yi=+1},同理,类别c2的特征 X c 2 = { x i ∣ y i = − 1 } X_{c_2} = \{x_i|y_i=-1 \} Xc2={ xi∣yi=−1},属于c1类别的数据个数为 N 1 N_1 N1,属于类别c2的数据个数为 N 2 N_2 N2,其中, N 1 + N 2 = N N_1+N_2 = N N1+N2=N。
特征X投影在w方向至一维: z i = w T x i , ∣ ∣ w ∣ ∣ = 1 z_i = w^Tx_i,\;\;||w|| = 1 zi=wTxi,∣∣w∣∣=1
全样本投影的均值 z ˉ = 1 N ∑ i = 1 N z i = 1 N ∑ i = 1 N w T x i \bar{z} = \frac{1}{N}\sum\limits_{i=1}^{N}z_i = \frac{1}{N}\sum\limits_{i=1}^{N}w^Tx_i zˉ=N1i=1∑Nzi=N1i=1∑NwTxi
全样本投影的协方差 S z = 1 N ∑ i = 1 N ( z i − z ˉ ) ( z i − z ˉ ) T = 1 N ∑ i = 1 N ( w T x i − z ˉ ) ( w T x i − z ˉ ) T S_z = \frac{1}{N}\sum\limits_{i=1}^{N}(z_i-\bar{z})(z_i-\bar{z})^T = \frac{1}{N}\sum\limits_{i=1}^{N}(w^Tx_i-\bar{z})(w^Tx_i-\bar{z})^T Sz=N1i=1∑N(zi−zˉ)(zi−zˉ)T=N1i=1∑N(wTxi−zˉ)(wTxi−zˉ)T
c1样本投影的均值 z 1 ˉ = 1 N 1 ∑ i = 1 N 1 z i = 1 N 1 ∑ i = 1 N 1 w T x i \bar{z_1} = \frac{1}{N_1}\sum\limits_{i=1}^{N_1}z_i = \frac{1}{N_1}\sum\limits_{i=1}^{N_1}w^Tx_i z1ˉ=N11i=1∑N1zi=N11i=1∑N1wTxi
c1样本投影的协方差 S z 1 = 1 N 1 ∑ i = 1 N 1 ( z i − z 1 ˉ ) ( z i − z 1 ˉ ) T = 1 N 1 ∑ i = 1 N 1 ( w T x i − z 1 ˉ ) ( w T x i − z 1 ˉ ) T S_{z_1} = \frac{1}{N_1}\sum\limits_{i=1}^{N_1}(z_i-\bar{z_1})(z_i-\bar{z_1})^T = \frac{1}{N_1}\sum\limits_{i=1}^{N_1}(w^Tx_i-\bar{z_1})(w^Tx_i-\bar{z_1})^T Sz1=N11i=1∑N1(zi−z1ˉ)(zi−z1ˉ)T=N11i=1∑N1(wTxi−z1ˉ)(wTxi−z1ˉ)T
c2样本投影的均值 z 2 ˉ = 1 N 2 ∑ i = 1 N 2 z i = 1 N 2 ∑ i = 1 N 2 w T x i \bar{z_2} = \frac{1}{N_2}\sum\limits_{i=1}^{N_2}z_i = \frac{1}{N_2}\sum\limits_{i=1}^{N_2}w^Tx_i z2ˉ=N21i=1∑N2zi=N21i=1∑N2wTxi
c2样本投影的协方差 S z 2 = 1 N 2 ∑ i = 1 N 2 ( z i − z 2 ˉ ) ( z i − z 2 ˉ ) T = 1 N 2 ∑ i = 1 N 2 ( w T x i − z 2 ˉ ) ( w T x i − z 2 ˉ ) T S_{z_2} = \frac{1}{N_2}\sum\limits_{i=1}^{N_2}(z_i-\bar{z_2})(z_i-\bar{z_2})^T = \frac{1}{N_2}\sum\limits_{i=1}^{N_2}(w^Tx_i-\bar{z_2})(w^Tx_i-\bar{z_2})^T Sz2=N21i=1∑N2(zi−z2ˉ)(zi−z2ˉ)T=N21i=1∑N2(wTxi−z2ˉ)(wTxi−z2ˉ)T
类间差距: ( z ˉ 1 − z ˉ 2 ) 2 (\bar{z}_1-\bar{z}_2)^2 (zˉ1−zˉ2)2
类内方差: S 1 + S 2 S_1 + S_2 S1+S2
由于线性判别分析的目标是同一类别内方差小,不同类别之间距离大,因此损失函数定义为:
J ( w ) = ( z ˉ 1 − z ˉ 2 ) 2 s 1 + s 2 = w T ( x ˉ c 1 − x ˉ c 2 ) ( x ˉ c 1 − x ˉ c 2 ) T w w T ( s c 1 + s c 2 ) w w ^ = a r g m a x w J ( w ) J(w) = \frac{(\bar{z}_1-\bar{z}_2)^2}{s_1+s_2} = \frac{w^T(\bar{x}_{c_1}-\bar{x}_{c_2})(\bar{x}_{c_1}-\bar{x}_{c_2})^Tw}{w^T(s_{c_1}+s_{c_2})w}\\ \;\;\; \hat{w} = argmax_w\;J(w) J(w)=s1+s2(zˉ1−zˉ2)2=wT(sc1+sc2)wwT(xˉc1−xˉc2)(xˉc1−xˉc2)Tww^=argmaxwJ(w)
记: S b = ( x ˉ c 1 − x ˉ c 2 ) ( x ˉ c 1 − x ˉ c 2 ) T , S w = ( s c 1 + s c 2 ) S_b = (\bar{x}_{c_1}-\bar{x}_{c_2})(\bar{x}_{c_1}-\bar{x}_{c_2})^T,\;S_w = (s_{c_1}+s_{c_2}) Sb=(xˉc1−xˉc2)(xˉc1−xˉc2)T,Sw=(sc1+sc2),因此 J ( w ) = w T S b w w T S w w J(w) = \frac{w^TS_bw}{w^TS_ww} J(w)=wTSwwwTSbw
让J(w)对w求导等于0,求出: w = S w − 1 ( x ˉ c 1 − x ˉ c 2 ) w = S_w^{-1}(\bar{x}_{c_1}-\bar{x}_{c_2}) w=Sw−1(xˉc1−xˉc2)
# 线性判别分析
'''
参数:
solver:{'svd','lsqr','eigen'},默认='svd'
solver的使用,可能的值:
'svd':奇异值分解(默认)。不计算协方差矩阵,因此建议将此求解器用于具有大量特征的数据。
'lsqr':最小二乘解,可以与收缩结合使用。
'eigen':特征值分解,可以与收缩结合使用。
'''
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
lda_iris = LinearDiscriminantAnalysis()
lda_iris.fit(X,y)
lda_iris.score(X,y)
0.98
朴素贝叶斯
在线性判别分析中,我们假设每种分类类别下的特征遵循同一个协方差矩阵,每两个特征之间是存在协方差的,因此在线性判别分析中各种特征是不是独立的。但是,朴素贝叶斯算法对线性判别分析作进一步的模型简化,它将线性判别分析中的协方差矩阵中的协方差全部变成0,只保留各自特征的方差,也就是朴素贝叶斯假设各个特征之间是不相关的。在之前所看到的偏差-方差理论中,我们知道模型的简化可以带来方差的减少但是增加偏差,因此朴素贝叶斯也不例外,它比线性判别分析模型的方差小,偏差大。虽然简化了模型,实际中使用朴素贝叶斯的案例非常多,甚至多于线性判别分析,例如鼎鼎大名的新闻分类,垃圾邮件分类等。
# 朴素贝叶斯
from sklearn.naive_bayes import GaussianNB
NB_iris = GaussianNB()
NB_iris.fit(X, y)
NB_iris.score(X,y)
0.96
决策树
与前面内容所讲的决策树回归大致是一样的,只是在回归问题中,选择分割点的标准是均方误差,但是在分类问题中,由于因变量是类别变量而不是连续变量,因此用均方误差显然不合适。
于是我们选择使用分类错误率作为指标,公式如下:
E = 1 − m a x k ( p ^ m k ) E = 1-max_k(\hat{p}_{mk}) E=1−maxk(p^mk)
但是在大量的事实证明:分类错误率在构建决策树时不够敏感,一般在实际中用如下两个指标代替:
(1) 基尼系数:
G = ∑ k = 1 K p ^ m k ( 1 − p ^ m k ) G = \sum\limits_{k=1}^{K} \hat{p}_{mk}(1-\hat{p}_{mk}) G=k=1∑Kp^mk(1−p^mk)
在基尼系数的定义中,我们发现这个指标衡量的是K个类别的总方差。不难发现,如果所有的 p ^ m k \hat{p}_{mk} p^mk的取值都接近0或者1,基尼系数会很小。因此基尼系数被视为衡量结点纯度的指标----如果他的取值小,那就意味着某个节点包含的观测值几乎来自同一个类别。
(2) 交叉熵:
可以替代基尼系数的指标是交叉熵,定义如下:
D = − ∑ k = 1 K p ^ m k l o g p ^ m k D = -\sum\limits_{k=1}^{K} \hat{p}_{mk}log\;\hat{p}_{mk} D=−k=1∑Kp^mklogp^mk
显然,如果所有的 p ^ m k \hat{p}_{mk} p^mk都接近于0或者1,那么交叉熵就会接近0。因此,和基尼系数一样,如果第m个结点的纯度越高,则交叉熵越小。事实证明,基尼系数和交叉熵在数值上时很接近的。
决策树分类算法的完整步骤:
a. 选择最优切分特征j以及该特征上的最优点s:
遍历特征j以及固定j后遍历切分点s,选择使得基尼系数或者交叉熵最小的(j,s)
b. 按照(j,s)分裂特征空间,每个区域内的类别为该区域内样本比例最多的类别。
c. 继续调用步骤1,2直到满足停止条件,就是每个区域的样本数小于等于5。
d. 将特征空间划分为J个不同的区域,生成分类树。
# 使用决策树算法对iris分类:
'''
criterion:{“gini”, “entropy”}, default=”gini”
max_depth:树的最大深度。
min_samples_split:拆分内部节点所需的最少样本数
min_samples_leaf :在叶节点处需要的最小样本数。
'''
from sklearn.tree import DecisionTreeClassifier
tree_iris = DecisionTreeClassifier(min_samples_leaf=5)
tree_iris.fit(X,y)
tree_iris.score(X,y)
0.9733333333333334
支持向量机SVM
简单点讲,SVM就是一种二类分类模型,他的基本模型是的定义在特征空间上的间隔最大的线性分类器,SVM的学习策略就是间隔最大化。
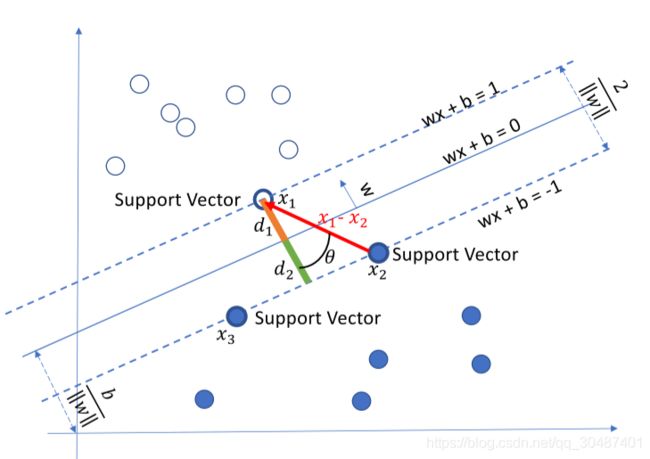
支持向量机的基本原理非常简单。如图所示,白色和蓝色的点各为一类,我们的目标是找到一个分割平面将两个类别分开。通常来说,如果数据本身是线性可分的,那么事实上存在无数个这样的超平面。这是因为给定一个分割平面稍微上移下移或旋转这个超平面,只要不接触这些观测点,仍然可以将数据分开。一个很自然的想法就是找到最大间隔超平面,即找到一个分割平面距离最近的观测点最远。
推导过程
下面我们来严格推导:
我们根据距离超平米那最近的点,只要同时缩放w和b可以得到: w T x 1 + b = 1 w^Tx_1 + b = 1 wTx1+b=1与 w T x 2 + b = − 1 w^Tx_2+b = -1 wTx2+b=−1,因此:
w T x 1 + b = 1 w T x 2 + b = − 1 ( w T x 1 + b ) − ( w T x 2 + b ) = 2 w T ( x 1 − x 2 ) = 2 w T ( x 1 − x 2 ) = ∥ w ∥ 2 ∥ x 1 − x 2 ∥ 2 cos θ = 2 ∥ x 1 − x 2 ∥ 2 cos θ = 2 ∥ w ∥ 2 d 1 = d 2 = ∥ x 1 − x 2 ∥ 2 cos θ 2 = 2 ∥ w ∥ 2 2 = 1 ∥ w ∥ 2 d 1 + d 2 = 2 ∥ w ∥ 2 \begin{array}{l} w^{T} x_{1}+b=1 \\ w^{T} x_{2}+b=-1 \\ \left(w^{T} x_{1}+b\right)-\left(w^{T} x_{2}+b\right)=2 \\ w^{T}\left(x_{1}-x_{2}\right)=2 \\ \qquad \begin{array}{l} w^{T}\left(x_{1}-x_{2}\right)=\|w\|_{2}\left\|x_{1}-x_{2}\right\|_{2} \cos \theta=2 \\ \left\|x_{1}-x_{2}\right\|_{2} \cos \theta=\frac{2}{\|w\|_{2}} \end{array} \\ \qquad \begin{array}{l} d_{1}=d_{2}=\frac{\left\|x_{1}-x_{2}\right\|_{2} \cos \theta}{2}=\frac{\frac{2}{\|w\|_{2}}}{2}=\frac{1}{\|w\|_{2}} \\ d_{1}+d_{2}=\frac{2}{\|w\|_{2}} \end{array} \end{array} wTx1+b=1wTx2+b=−1(wTx1+b)−(wTx2+b)=2wT(x1−x2)=2wT(x1−x2)=∥w∥2∥x1−x2∥2cosθ=2∥x1−x2∥2cosθ=∥w∥22d1=d2=2∥x1−x2∥2cosθ=2∥w∥22=∥w∥21d1+d2=∥w∥22
由此可知道SVM模型的具体形式:
min w , b 1 2 ∥ w ∥ 2 s.t. y ( i ) ( w T x ( i ) + b ) ≥ 1 , i = 1 , … , n \begin{aligned} \min _{w, b} & \frac{1}{2}\|w\|^{2} \\ \text { s.t. } & y^{(i)}\left(w^{T} x^{(i)}+b\right) \geq 1, \quad i=1, \ldots, n \end{aligned} w,bmin s.t. 21∥w∥2y(i)(wTx(i)+b)≥1,i=1,…,n
可以将约束条件写为: $g_{i}(w)=-y{(i)}\left(w{T} x^{(i)}+b\right)+1 \leq 0 $
可以将优化问题拉格朗日化
L ( w , b , α ) = 1 2 ∥ w ∥ 2 − ∑ i = 1 n α i [ y ( i ) ( w T x ( i ) + b ) − 1 ] \mathcal{L}(w, b, \alpha)=\frac{1}{2}\|w\|^{2}-\sum_{i=1}^{n} \alpha_{i}\left[y^{(i)}\left(w^{T} x^{(i)}+b\right)-1\right] L(w,b,α)=21∥w∥2−i=1∑nαi[y(i)(wTx(i)+b)−1]
因此:
L ( w , b , α ) = 1 2 ∥ w ∥ 2 − ∑ i = 1 n α i [ y ( i ) ( w T x ( i ) + b ) − 1 ] \mathcal{L}(w, b, \alpha)=\frac{1}{2}\|w\|^{2}-\sum_{i=1}^{n} \alpha_{i}\left[y^{(i)}\left(w^{T} x^{(i)}+b\right)-1\right] L(w,b,α)=21∥w∥2−i=1∑nαi[y(i)(wTx(i)+b)−1]
欲构造 dual 问题, 首先求拉格朗日化的问题中 $\mathrm{w} $ 和 $\mathrm{b} $ 的值, 对 $ \mathrm{w}$ 求梯度, 令梯度为 0, 可求得 w:
对 b 求梯度, 令梯度为 0, 可得:
∂ ∂ b L ( w , b , α ) = ∑ i = 1 n α i y ( i ) = 0 \frac{\partial}{\partial b} \mathcal{L}(w, b, \alpha)=\sum_{i=1}^{n} \alpha_{i} y^{(i)}=0 ∂b∂L(w,b,α)=i=1∑nαiy(i)=0
将 w \mathrm{w} w 带入拉格朗日化的原问题可得
L ( w , b , α ) = ∑ i = 1 n α i − 1 2 ∑ i , j = 1 n y ( i ) y ( j ) α i α j ( x ( i ) ) T x ( j ) − b ∑ i = 1 n α i y ( i ) L ( w , b , α ) = ∑ i = 1 n α i − 1 2 ∑ i , j = 1 n y ( i ) y ( j ) α i α j ( x ( i ) ) T x ( j ) \begin{array}{l} \mathcal{L}(w, b, \alpha)=\sum_{i=1}^{n} \alpha_{i}-\frac{1}{2} \sum_{i, j=1}^{n} y^{(i)} y^{(j)} \alpha_{i} \alpha_{j}\left(x^{(i)}\right)^{T} x^{(j)}-b \sum_{i=1}^{n} \alpha_{i} y^{(i)} \\ \mathcal{L}(w, b, \alpha)=\sum_{i=1}^{n} \alpha_{i}-\frac{1}{2} \sum_{i, j=1}^{n} y^{(i)} y^{(j)} \alpha_{i} \alpha_{j}\left(x^{(i)}\right)^{T} x^{(j)} \end{array} L(w,b,α)=∑i=1nαi−21∑i,j=1ny(i)y(j)αiαj(x(i))Tx(j)−b∑i=1nαiy(i)L(w,b,α)=∑i=1nαi−21∑i,j=1ny(i)y(j)αiαj(x(i))Tx(j)
因此:
对拉格朗日化的原问题求最小值, 得到了 w , 现在可以构造 dual 问題 max α W ( α ) = ∑ i = 1 n α i − 1 2 ∑ i , j = 1 n y ( i ) y ( j ) α i α j ⟨ x ( i ) , x ( j ) ⟩ s.t. α i ≥ 0 , i = 1 , … , n ∑ i = 1 n α i y ( i ) = 0 可以推导出 b的值为: b ∗ = − max i : y ( i ) = − 1 w ∗ T x ( i ) + min i : y ( i ) = 1 w ∗ T x ( i ) 2 SVM的决策子如下,值的符号为类别. w T x + b = ( ∑ i = 1 n α i y ( i ) x ( i ) ) T x + b = ∑ i = 1 n α i y ( i ) ⟨ x ( i ) , x ⟩ + b \begin{aligned} &\text { 对拉格朗日化的原问题求最小值, 得到了 } \mathrm{w} \text { , 现在可以构造 dual 问題 }\\ &\begin{aligned} \max _{\alpha} & W(\alpha)=\sum_{i=1}^{n} \alpha_{i}-\frac{1}{2} \sum_{i, j=1}^{n} y^{(i)} y^{(j)} \alpha_{i} \alpha_{j}\left\langle x^{(i)}, x^{(j)}\right\rangle \\ \text { s.t. } & \alpha_{i} \geq 0, \quad i=1, \ldots, n \\ & \sum_{i=1}^{n} \alpha_{i} y^{(i)}=0 \end{aligned}\\ &\text { 可以推导出 b的值为: } b^{*}=-\frac{\max _{i: y^{(i)}=-1} w^{* T} x^{(i)}+\min _{i: y^{(i)}=1} w^{* T} x^{(i)}}{2}\\ &\begin{array}{r} \text { SVM的决策子如下,值的符号为类别. } \\ \qquad w^{T} x+b=\left(\sum_{i=1}^{n} \alpha_{i} y^{(i)} x^{(i)}\right)^{T} x+b=\sum_{i=1}^{n} \alpha_{i} y^{(i)}\left\langle x^{(i)}, x\right\rangle+b \end{array} \end{aligned} 对拉格朗日化的原问题求最小值, 得到了 w , 现在可以构造 dual 问題 αmax s.t. W(α)=i=1∑nαi−21i,j=1∑ny(i)y(j)αiαj⟨x(i),x(j)⟩αi≥0,i=1,…,ni=1∑nαiy(i)=0 可以推导出 b的值为: b∗=−2maxi:y(i)=−1w∗Tx(i)+mini:y(i)=1w∗Tx(i) SVM的决策子如下,值的符号为类别. wTx+b=(∑i=1nαiy(i)x(i))Tx+b=∑i=1nαiy(i)⟨x(i),x⟩+b
非线性支持向量机
在刚刚的讨论中,我们都是着重讨论了线性支持向量机是如何工作的,但是在现实生活中,我们很难碰到线性可分的数据集,如:

那我们应该如何处理非线性问题呢?答案就是将数据投影至更加高的维度!
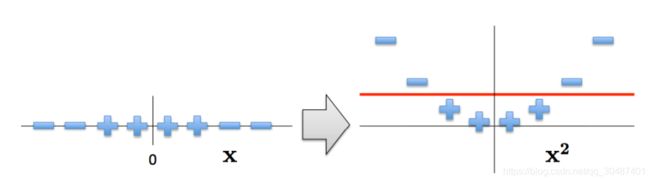
上图中,在一维数据做不到线性可分,我们将数据投影至二维平面就可以成功线性可分。那么,我们来详细探讨下这其中的奥妙:
Φ : X ↦ X ^ = Φ ( x ) Φ ( [ x i 1 , x i 2 ] ) = [ x i 1 , x i 2 , x i 1 x i 2 , x i 1 2 , x i 2 2 ] \begin{array}{l} \Phi: \mathcal{X} \mapsto \hat{\mathcal{X}}=\Phi(\mathbf{x}) \\ \Phi\left(\left[x_{i 1}, x_{i 2}\right]\right)=\left[x_{i 1}, x_{i 2}, x_{i 1} x_{i 2}, x_{i 1}^{2}, x_{i 2}^{2}\right] \end{array} Φ:X↦X^=Φ(x)Φ([xi1,xi2])=[xi1,xi2,xi1xi2,xi12,xi22]
如果我们使用上面公式的形式将低维数据拓展至高维数据,则必须面临一个很大的问题,那就是:维度爆炸导致的计算量太大的问题。假如是一个2维特征的数据,我们可以将其映射到5维来做特征的内积,如果原始空间是三维,可以映射到到19维空间,似乎还可以处理。但是如果我们的低维特征是100个维度,1000个维度呢?那么我们要将其映射到超级高的维度来计算特征的内积。这时候映射成的高维维度是爆炸性增长的,这个计算量实在是太大了,而且如果遇到无穷维的情况,就根本无从计算了。能不能呢个避免这个问题呢?核函数隆重登场:
回顾线性可分SVM的优化目标函数:
m i n ⏟ α 1 2 ∑ i = 1 , j = 1 m α i α j y i y j x i ∙ x j − ∑ i = 1 m α i s . t . ∑ i = 1 m α i y i = 0 0 ≤ α i ≤ C \underbrace{ min }_{\alpha} \frac{1}{2}\sum\limits_{i=1,j=1}^{m}\alpha_i\alpha_jy_iy_jx_i \bullet x_j - \sum\limits_{i=1}^{m}\alpha_i\\ s.t. \; \sum\limits_{i=1}^{m}\alpha_iy_i = 0\\ 0 \leq \alpha_i \leq C α min21i=1,j=1∑mαiαjyiyjxi∙xj−i=1∑mαis.t.i=1∑mαiyi=00≤αi≤C
注意到上式低维特征仅仅以内积 x i ∙ x j x_i \bullet x_j xi∙xj 的形式出现,如果我们定义一个低维特征空间到高维特征空间的映射 ϕ \phi ϕ,将所有特征映射到一个更高的维度,让数据线性可分,我们就可以继续按前两篇的方法来优化目标函数,求出分离超平面和分类决策函数了。也就是说现在的SVM的优化目标函数变成:
min ⏟ α 1 2 ∑ i = 1 , j = 1 m α i α j y i y j ϕ ( x i ) ∙ ϕ ( x j ) − ∑ i = 1 m α i s. t . ∑ i = 1 m α i y i = 0 0 ≤ α i ≤ C \begin{array}{c} \underbrace{\min }_{\alpha} \frac{1}{2} \sum_{i=1, j=1}^{m} \alpha_{i} \alpha_{j} y_{i} y_{j} \phi\left(x_{i}\right) \bullet \phi\left(x_{j}\right)-\sum_{i=1}^{m} \alpha_{i} \\ \text { s. } t . \sum_{i=1}^{m} \alpha_{i} y_{i}=0 \\ 0 \leq \alpha_{i} \leq C \end{array} α min21∑i=1,j=1mαiαjyiyjϕ(xi)∙ϕ(xj)−∑i=1mαi s. t.∑i=1mαiyi=00≤αi≤C
可以看到,和线性可分SVM的优化目标函数的区别仅仅是将内积 x i ∙ x j x_i \bullet x_j xi∙xj替换为 ϕ ( x i ) ∙ ϕ ( x j ) \phi(x_i) \bullet \phi(x_j) ϕ(xi)∙ϕ(xj)。我们要将其映射到超级高的维度来计算特征的内积。这时候映射成的高维维度是爆炸性增长的,这个计算量实在是太大了,而且如果遇到无穷维的情况,就根本无从计算了。下面引入核函数:
假设 ϕ \phi ϕ是一个从低维的输入空间 χ \chi χ(欧式空间的子集或者离散集合)到高维的希尔伯特空间的 H \mathcal{H} H映射。那么如果存在函数 K ( x , z ) K(x,z) K(x,z),对于任意 x , z ∈ χ x, z \in \chi x,z∈χ,都有:
K ( x , z ) = ϕ ( x ) ∙ ϕ ( z ) K(x, z) = \phi(x) \bullet \phi(z) K(x,z)=ϕ(x)∙ϕ(z)
那么我们就称 K ( x , z ) K(x, z) K(x,z)为核函数。
仔细发现, K ( x , z ) K(x, z) K(x,z)的计算是在低维特征空间来计算的,它避免了在刚才我们提到了在高维维度空间计算内积的恐怖计算量。也就是说,我们可以好好享受在高维特征空间线性可分的利益,却避免了高维特征空间恐怖的内积计算量。下面介绍几种常用的核函数:
(1) 多项式核函数:
多项式核函数(Polynomial Kernel)是线性不可分SVM常用的核函数之一,表达式为:
K ( x i , x j ) = ( ⟨ x i , x j ⟩ + c ) d K\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right)=\left(\left\langle\mathbf{x}_{i}, \mathbf{x}_{j}\right\rangle+c\right)^{d} K(xi,xj)=(⟨xi,xj⟩+c)d
C用来控制低阶项的强度,C=0,d=1代表无核函数。
(2) 高斯核函数:
高斯核函数(Gaussian Kernel),在SVM中也称为径向基核函数(Radial Basis Function,RBF),它是非线性分类SVM最主流的核函数。libsvm默认的核函数就是它。表达式为:
K ( x i , x j ) = exp ( − ∥ x i − x j ∥ 2 2 2 σ 2 ) K\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right)=\exp \left(-\frac{\left\|\mathbf{x}_{i}-\mathbf{x}_{j}\right\|_{2}^{2}}{2 \sigma^{2}}\right) K(xi,xj)=exp(−2σ2∥xi−xj∥22)
使用高斯核函数之前需要将特征标准化,因此这里衡量的是样本之间的相似度。
(3) Sigmoid核函数:
Sigmoid核函数(Sigmoid Kernel)也是线性不可分SVM常用的核函数之一,表达式为:
K ( x i , x j ) = tanh ( α x i ⊤ x j + c ) K\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right)=\tanh \left(\alpha \mathbf{x}_{i}^{\top} \mathbf{x}_{j}+c\right) K(xi,xj)=tanh(αxi⊤xj+c)
此时的SVM相当于没有隐藏层的简单神经网络。
(4) 余弦相似度核:
常用于衡量两段文字的余弦相似度,表达式为:
K ( x i , x j ) = x i ⊤ x j ∥ x i ∥ ∥ x j ∥ K\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right)=\frac{\mathbf{x}_{i}^{\top} \mathbf{x}_{j}}{\left\|\mathbf{x}_{i}\right\|\left\|\mathbf{x}_{j}\right\|} K(xi,xj)=∥xi∥∥xj∥xi⊤xj
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
'''
C:正则化参数。正则化的强度与C成反比。必须严格为正。惩罚是平方的l2惩罚。
kernel:{'linear','poly','rbf','sigmoid','precomputed'},默认='rbf'
degree:多项式和的阶数
gamma:“ rbf”,“ poly”和“ Sigmoid”的内核系数。
shrinking:是否软间隔分类,默认true
'''
svc_iris = make_pipeline(StandardScaler(), SVC(gamma='auto'))
svc_iris.fit(X, y)
svc_iris.score(X,y)
0.9733333333333334
小结
这个task重点介绍了各种具体的分类模型,理解难度不大,但是相关推导应当认真去推一遍