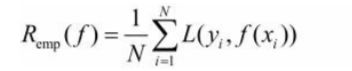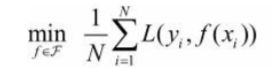模型之母：简单线性回归&最小二乘法

模型之母：简单线性回归&最小二乘法

本文为数据茶水间群友原创，经授权在本公众号发表。

关于作者：Japson。某人工智能公司AI平台研发工程师，专注于AI工程化及场景落地。持续学习中，期望与大家多多交流技术以及职业规划。

0x00 前言

I‘m Linear Regression, One of the most important mathematical models and Mother of Models.

线性回归模型看起来非常简单，简单到让人怀疑其是否有研究价值以及使用价值。但实际上，线性回归模型可以说是最重要的数学模型之一，很多模型都是建立在它的基础之上，可以被称为是“模型之母”。

那么本篇文章，将会学习到简单线性回归，从中总结出一类机器学习算法的基本思路并引出损失函数的概念。为了求出最小的损失函数，将会学习到大名鼎鼎的最小二乘法。

0x01 简单线性回归

1.1 什么是简单线性回归

之前我们介绍的kNN算法属于分类(Classification)，即label为离散的类别型(categorical variable)，如：颜色类别、手机品牌、是否患病等。

而简单线性回归是属于回归(regression)，即label为连续数值型(continuous numerical variable)，如：房价、股票价格、降雨量等。

那么什么是简单线性回归？

所谓简单，是指只有一个样本特征，即只有一个自变量；所谓线性，是指方程是线性的；所谓回归，是指用方程来模拟变量之间是如何关联的。

简单线性回归，其思想简单，实现容易（与其背后强大的数学性质相关。同时也是许多强大的非线性模型（多项式回归、逻辑回归、SVM）的基础。并且其结果具有很好的可解释性。

1.2 求解思路

下面我们可以用一个简单的例子来直观理解线性回归模型。

小A开了一家玩具厂，他想分析一下玩具产量与成本之间的关系，于是小A制作了如下表格：

玩具个数	成本
10	7.7
10	9.87
11	10.87
12	12.18
13	11.43
14	13.36
15	15.15
16	16.73
17	17.4

为了更加直观地了解数据，小A对数据进行了可视化：

从图像中我们可以发现，产量和成本之间，存在着一定的线性关系，似乎是在沿着某条直线上下随机波动。

4a2ed38d27a9d50786338c630bd3db1c

也就是说，我们需要一条直线，最大程度的拟合样本特征和样本数据标记之间的关系。 在二维平面中，这条直线的方程就是 y = ax + b

假设我们找到了最佳拟合的直线方程：y = ax + b

则对于每个样本点 ，根据我们的直线方程，预测值为：

很显然，我们希望直线方程能够尽可能地拟合真实情况，也就是说真值  和预测值  的差距尽量小。只有所有的样本的误差都小，才能证明我们找出的直线方程拟合性好。

通常来说，为了防止正误差值和负误差值相抵的情况，使用绝对值来表示距离：，但是在线性回归中，我们需要找极值，需要函数可导，而  不是一个处处可导的函数，因此很自然地想到可以使用：

考虑所有样本，我们推导出：

因此我们目标是：已知训练数据样本x、y ，找到a和b的值，使  尽可能小，从而得出最佳的拟合方程。

b5fdbf785997e6b43dd963736442975b

1.3 一种基本推导思路

在上一小节中，找到一组参数，使得真实值与预测值之间的差距尽可能地小，是一种典型的机器学习算法的推导思路

**我们所谓的建模过程，其实就是找到一个模型，最大程度的拟合我们的数据。**在简单线回归问题中，模型就是我们的直线方程：y = ax + b 。

要想最大的拟合数据，本质上就是找到没有拟合的部分，也就是损失的部分尽量小，就是损失函数（loss function）（也有算法是衡量拟合的程度，称函数为效用函数（utility function））：

因此，推导思路为：

1. 通过分析问题，确定问题的损失函数或者效用函数；
2. 然后通过最优化损失函数或者效用函数，获得机器学习的模型

近乎所有参数学习算法都是这样的套路，区别是模型不同，建立的目标函数不同，优化的方式也不同。

回到简单线性回归问题，目标：

已知训练数据样本、 ，找到和的值，使  尽可能小

这是一个典型的最小二乘法问题（最小化误差的平方）

通过最小二乘法可以求出a、b的表达式：

0x02 最小二乘法

2.1 由损失函数引出一堆“风险”

2.1.1 损失函数

在机器学习中，所有的算法模型其实都依赖于最小化或最大化某一个函数，我们称之为“目标函数”。

最小化的这组函数被称为“损失函数”。什么是损失函数呢？

损失函数描述了单个样本预测值和真实值之间误差的程度。用来度量模型一次预测的好坏。

损失函数是衡量预测模型预测期望结果表现的指标。损失函数越小，模型的鲁棒性越好。。

常用损失函数有：

• 0-1损失函数：用来表述分类问题，当预测分类错误时，损失函数值为1，正确为0

• 平方损失函数：用来描述回归问题，用来表示连续性变量，为预测值与真实值差值的平方。（误差值越大、惩罚力度越强，也就是对差值敏感）

• 绝对损失函数：用在回归模型，用距离的绝对值来衡量

• 对数损失函数：是预测值Y和条件概率之间的衡量。事实上，该损失函数用到了极大似然估计的思想。P(Y|X)通俗的解释就是：在当前模型的基础上，对于样本X，其预测值为Y，也就是预测正确的概率。由于概率之间的同时满足需要使用乘法，为了将其转化为加法，我们将其取对数。最后由于是损失函数，所以预测正确的概率越高，其损失值应该是越小，因此再加个负号取个反。

以上损失函数是针对于单个样本的，但是一个训练数据集中存在N个样本，N个样本给出N个损失，如何进行选择呢？

这就引出了风险函数。

2.1.2 期望风险

期望风险是损失函数的期望，用来表达理论上模型f(X)关于联合分布P(X,Y)的平均意义下的损失。又叫期望损失/风险函数。

2b1aec01d04a4e2ff3d2f2db7bef3b56

2.1.3 经验风险

模型f(X)关于训练数据集的平均损失，称为经验风险或经验损失。

其公式含义为：模型关于训练集的平均损失（每个样本的损失加起来，然后平均一下）

3d6ab76d780a23042d1bf145b8e7744f

经验风险最小的模型为最优模型。在训练集上最小经验风险最小，也就意味着预测值和真实值尽可能接近，模型的效果越好。公式含义为取训练样本集中对数损失函数平均值的最小。

f8905ef66a7d825079f1375250b5c37e

2.1.4 经验风险最小化和结构风险最小化

期望风险是模型关于联合分布的期望损失，经验风险是模型关于训练样本数据集的平均损失。根据大数定律，当样本容量N趋于无穷时，经验风险趋于期望风险。

因此很自然地想到用经验风险去估计期望风险。但是由于训练样本个数有限，可能会出现过度拟合的问题，即决策函数对于训练集几乎全部拟合，但是对于测试集拟合效果过差。因此需要对其进行矫正：

• 结构风险最小化：当样本容量不大的时候，经验风险最小化容易产生“过拟合”的问题，为了“减缓”过拟合问题，提出了 结构风险最小理论。结构风险最小化为经验风险与复杂度同时较小。

3c0c72d9d5e9e71f56431d4d1b4d1ae9

通过公式可以看出，结构风险：在经验风险上加上一个正则化项(regularizer)，或者叫做罚项(penalty) 。正则化项是J(f)是函数的复杂度再乘一个权重系数（用以权衡经验风险和复杂度）

2.1.5 小结

1、损失函数：单个样本预测值和真实值之间误差的程度。

2、期望风险：是损失函数的期望，理论上模型f(X)关于联合分布P(X,Y)的平均意义下的损失。

3、经验风险：模型关于训练集的平均损失（每个样本的损失加起来，然后平均一下）。

4、结构风险：在经验风险上加上一个正则化项，防止过拟合的策略。

2.2 最小二乘法

2.2.1 什么是最小二乘法

言归正传，进入最小二乘法的部分。

大名鼎鼎的最小二乘法，虽然听上去挺高大上，但是思想还是挺朴素的，符合大家的直觉。

最小二乘法源于法国数学家阿德里安的猜想：

对于测量值来说，让总的误差的平方最小的就是真实值。这是基于，如果误差是随机的，应该围绕真值上下波动。

即：

那么为了求助这个二次函数的最小值，对其进行求导，导数为0的时候取得最小值：进而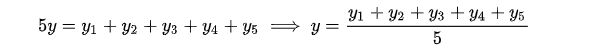：正好是算数平均数（算数平均数是最小二乘法的特例）。

这就是最小二乘法，所谓“二乘”就是平方的意思。

（高斯证明过：如果误差的分布是正态分布，那么最小二乘法得到的就是最有可能的值。）

2.2.2 线性回归中的应用

我们在第一章中提到：

目标是，找到a和b，使得损失函数：尽可能的小。

这里，将简单线性问题转为最优化问题。下面对函数的各个位置分量求导，导数为0的地方就是极值：

对  进行求导：

然后mb提到等号前面，两边同时除以m，等号右面的每一项相当于均值。

现在 对  进行求导：

此时将对  进行求导得到的结果 代入上式中，得到： 

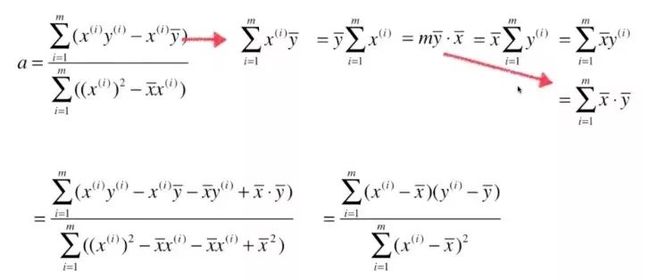
将上式进行整理，得到

9d4160c6f80a288fc7db7f5a35265211

将上式继续进行整理：

这样在实现的时候简单很多。

最终我们通过最小二乘法得到a、b的表达式：

0xFF 总结

本章中，我们从数学的角度了解了简单线性回归，从中总结出一类机器学习算法的基本思路：

1. 通过分析问题，确定问题的损失函数或者效用函数；
2. 然后通过最优化损失函数或者效用函数，获得机器学习的模型。

理解了损失函数的概念，并列举出了常见损失函数，并引出了一堆“风险”。最后为了求出最小的损失函数，学习了最小二乘法，并进行了完整的数学推导。

下一篇，我们将会实现简单线性回归，并添加到我们自己的工程文件里（其实下一篇应该是本篇的内容，但是由于本篇内容设计了太多的LateX公式，我的印象笔记实在是太太太卡了，写不下去了t.t）

热门文章