基于卷积神经网络CNN的手写数字识别

1.CNN卷积神经网络中的几个概念

想象现在你有一张手写数字图片，你需要识别它是0-9中的哪个数字，一种思路是寻找图片局部的特征，如果这个图片和某个数字的大部分局部特征最相似，则将该图片识别为该数字。

卷积核(Convolution Kernel)

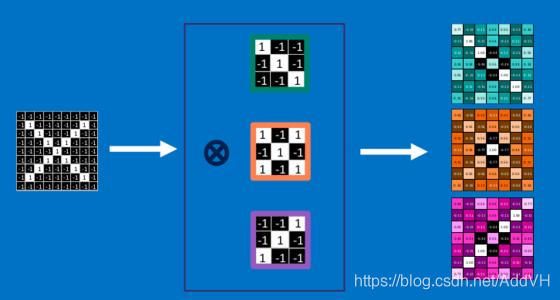
卷积核就是判断为哪个数字所需要的图片的局部特征，不过CNN中卷积核的选择是由根据大量数据训练生成的，而不是我们人类根据经验选定的。如下图所示，中间三个小片段就是所谓的卷积核，就好比一块块小的拼图碎片，需要在被识别的图片中寻找相似的片段来决定和哪个数字相似。

卷积(Convolution)

通俗的说，寻找局部相似片段的过程就叫做卷积，我的理解就是拿着上面的片段(卷积核)在被识别的图片上从上到下，从左到右比对一遍(这里还涉及到步长、边界补零等)。那么，如何将“比对”用数学运算来表示呢？如下图所示，将卷积核与图片相应位置分别做乘法后累加，累加的结果表征比对的“相似程度”。在原图经过标准化的情况下(数据标准化到-1与1之间)，结果越接近1，说明原图的这个局部与要寻找的片段(卷积核)越相似，比如上图右边计算结果代表的格子越白(越接近1)，原图该部位与相应卷积核越相似。

池化(Pooling)

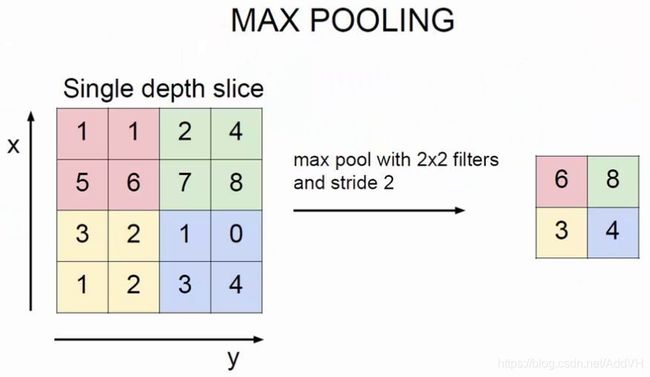
什么是池化呢？我目前的理解是一种降维方法。在保留原图大部分特征的前提下，降低图片的尺寸，以达到减少运算量的目的。池化主要有最大值池化和平均值池化两种方法，如下图所示是最大值池化，将原图2X2方格中的最大值代表该局部的值，生成新的图片。这样就将原图4X4大小的数据降维到2X2大小，虽然数据信息减少了，但原图的重要特征任然保留。你可能感觉这种方法没什么大的作用，但当图片极其庞大，信息量巨大的情况下，池化是优化算法，减轻运算量的一种重要手段。

2.导入mnist手写数据集

#导入相应模块和数据集
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
mnist=input_data.read_data_sets('mnist_data',one_hot=True)

由于数据集较大，只选择一部分数据进行训练和测试

#获得训练集和测试集
X_train,y_train = mnist.train.images[:3000], mnist.train.labels[:3000]
X_test,y_test = mnist.test.images[:1000], mnist.test.labels[:1000]

#定义输出图片函数
def print_digits(images, y, max_n=10):
    # 图片尺寸
    fig = plt.figure(figsize=(12, 12)) # 宽，高，英寸为单位
    fig.subplots_adjust(left=0, right=1, bottom=0, top=1, hspace=0.05, wspace=0.05)
    i = 0
    while i <max_n and i <images.shape[0]:
        # 绘图
        p = fig.add_subplot(20, 20, i + 1, xticks=[], yticks=[])
        p.imshow(images[i].reshape(28,28), cmap=plt.cm.bone)
        i = i + 1

#查看训练集前100张
print_digits(X_train,y_train,100)

3.构建卷积神经网络

构建神经网络前先画出其大体形态如下图所示(本例中只使用一层卷积+池化)。

然后根据所画的图依次构建各层

#定义输入、输出
input_x=tf.placeholder(tf.float32,[None,28*28])/255.
#输出是一个one_hot的向量
output_y=tf.placeholder(tf.int32,[None,10])

#输入层 [28*28*1]
input_x_images=tf.reshape(input_x,[-1,28,28,1])

#卷积层
#conv1 5*5*32
conv1=tf.layers.conv2d(
    inputs=input_x_images,
    filters=32,
    kernel_size=[5,5],
    strides=1,
    padding='same',
    activation=tf.nn.relu
)

各参数含义：
inputs 输入，是一个向量
filters 卷积核个数，也就是卷积层的厚度
kernel_size 卷积核的尺寸
strides: 扫描步长
padding: 边界补0，valid不需要补0，same需要补0
activation: 激活函数

#池化层
pool1=tf.layers.max_pooling2d(
    inputs=conv1,
    pool_size=[2,2],
    strides=2
)

各参数含义：
inputs 输入，张量必须要有四个维度
pool_size: 过滤器的尺寸
strides: 步长

#扁平化
flat=tf.reshape(pool1,[-1,14*14*32]
#形状变成了[?,6272]

#全连接层 
#inputs: 张量
#units： 神经元的个数
#activation: 激活函数
dense=tf.layers.dense(
    inputs=flat,
    units=1024,
    activation=tf.nn.relu
)

#输出层（本质是一个全连接层）
logits=tf.layers.dense(
    inputs=dense,
    units=10
)
#形状[?,10]

#计算误差 cross entropy（交叉熵），再用Softmax计算百分比的概率
#onehot_labels: 标签值
#logits: 神经网络的输出值
loss=tf.losses.softmax_cross_entropy(onehot_labels=output_y,logits=logits)
# 用Adam优化器来最小化误差,学习率0.001 类似梯度下降
train_op=tf.train.GradientDescentOptimizer(learning_rate=0.001).minimize(loss)

#精度,计算预测值和实际标签的匹配程度
#labels：真实标签
#predictions: 预测值
#Return: (accuracy,update_op)accuracy 是一个向量准确率，update_op 是一个op可以求出精度。
accuracy_op=tf.metrics.accuracy(
    labels=tf.argmax(output_y,axis=1),
    predictions=tf.argmax(logits,axis=1)
)[1]

4.训练卷积神经网络

#创建会话
sess=tf.Session()
#初始化全局和局部变量
init=tf.group(tf.global_variables_initializer(),
              tf.local_variables_initializer())
sess.run(init)

#迭代50000次
for i in range(50000):
    batch=mnist.train.next_batch(50)
    train_loss,train_operation=sess.run([loss,train_op],{
     input_x:batch[0],output_y:batch[1]})
    if i%1000 == 0:
        train_accuracy=sess.run(accuracy_op,{
     input_x:X_train,output_y:y_train})
        print("Step = %d, Train loss = %.4f,[Train accuracy = %.2f]" %(i,train_loss,train_accuracy))

Step = 0, Train loss = 2.2904,[Train accuracy = 0.13]
Step = 1000, Train loss = 1.2188,[Train accuracy = 0.47]
Step = 2000, Train loss = 0.5437,[Train accuracy = 0.60]
Step = 3000, Train loss = 0.5143,[Train accuracy = 0.67]
Step = 4000, Train loss = 0.2612,[Train accuracy = 0.72]
Step = 5000, Train loss = 0.4200,[Train accuracy = 0.75]
......
Step = 44000, Train loss = 0.0969,[Train accuracy = 0.92]
Step = 45000, Train loss = 0.1404,[Train accuracy = 0.93]
Step = 46000, Train loss = 0.0506,[Train accuracy = 0.93]
Step = 47000, Train loss = 0.0290,[Train accuracy = 0.93]
Step = 48000, Train loss = 0.0867,[Train accuracy = 0.93]
Step = 49000, Train loss = 0.0935,[Train accuracy = 0.93]

5.使用测试集测试

test_accuracy=sess.run(accuracy_op,{
     input_x:X_test,output_y:y_test})
print(test_accuracy)

0.9292303

可以看到，训练集准确率达到92%，说明对测试集的识别效果也较好

#查看测试集前20张
print_digits(X_test,y_test,20)

#输出测试集前20个的预测值
test_output = sess.run(logits,{
     input_x:X_test[:20]})
y_pred = np.argmax(test_output,1)
print(y_pred,'predicted numbers')
print(np.argmax(y_test[:20],1),'real numbers')
sess.close()

[7 2 1 0 4 1 4 9 6 9 0 6 9 0 1 5 9 7 3 4] predicted numbers
[7 2 1 0 4 1 4 9 5 9 0 6 9 0 1 5 9 7 3 4] real numbers

可以看出，对手写数字的识别效果较好。该卷积神经网络只使用了一层卷积+池化层，可以继续尝试使用多层卷积+池化层进行优化

6.参考文献

[1] 使用tensorflow实现CNN
[2] tensorflow中文文档