深度学习--TensorFlow（项目）Keras手写数字识别

目录

效果展示

基础理论

1、softmax激活函数

2、神经网络

3、隐藏层及神经元最佳数量

 一、数据准备

1、载入数据集

2、数据处理

2-1、归一化

2-2、独热编码

二、神经网络拟合

1、搭建神经网络

2、设置优化器、损失函数

3、训练

三、预测

1、备份图像数据集

2、预测分类

3、显示结果(plt)

总代码

---

效果展示

基础理论

本次手写数字识别，采用的是MNIST数据集。

http://yann.lecun.com/exdb/mnist/ 

1、softmax激活函数

这里输出层用到了softmax激活函数，把输出的数据转化成概率：

2、神经网络

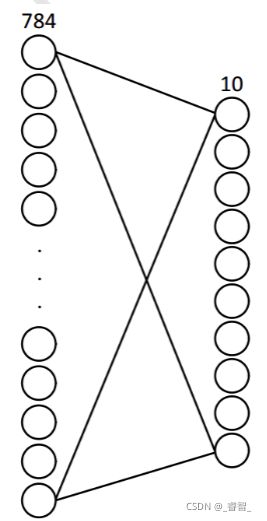
神经网络原型：

28*28=784个输入像素对应784个输入神经元；10个输出神经元分别对应0~9的十个数。

（为了提高训练的准确度，我加了一些隐藏层 ）

3、隐藏层及神经元最佳数量

        隐藏层、神经元最佳数量需要自己不断实验获得，先选取小一点的数据，欠拟合，再不断增加数据，直到最佳数据出现（即将出现过拟合情况）。

通常：

 一、数据准备

# 数据准备
def Data_Preparation():
    global train_data, train_label, test_data, test_label, mnist_train, \
        mnist_test, images, labels

1、载入数据集

# 1、载入数据集
    mnist = tf.keras.datasets.mnist
    (train_data, train_label), (test_data, test_label) = mnist.load_data()
    # 训练集数据 train_data 的数据形状为(60000，28，28)
    # 训练集标签 train_label 的数据形状为(60000)
    # 测试集数据 test_data 的数据形状为(10000，28，28)
    # 测试集标签 test_label 的数据形状为(10000)
    images, labels = test_data, test_label

2、数据处理

2-1、归一化

# 2-1、数据集归一化
    train_data = train_data/255
    test_data = test_data/255

2-2、独热编码

0~9分别用10个二进制数中1的位置表示它们的值。

# 2-2、标签独热编码
    train_label = tf.keras.utils.to_categorical(train_label, num_classes=10)
    test_label = tf.keras.utils.to_categorical(test_label, num_classes=10)
    #                           转化为独热编码   待转数据      独热码长度

二、神经网络拟合

1、搭建神经网络

输入层（数据展平：(28,28)->(784)）、隐藏层、输出层（10个神经元对应10个数字）。

# 1、创建神经网络
    model = tf.keras.models.Sequential([
        tf.keras.layers.Flatten(input_shape=(28, 28)),   # 输入数据压缩，三维变二维
        # (60000,28,28) -> (60000, 784)
        tf.keras.layers.Dense(200 + 1, activation=tf.nn.relu),
        tf.keras.layers.Dense(200 + 1, activation=tf.nn.relu),
        tf.keras.layers.Dense(200 + 1, activation=tf.nn.relu),
        tf.keras.layers.Dense(100 + 1, activation=tf.nn.relu),
        tf.keras.layers.Dense(100 + 1, activation=tf.nn.relu),
        tf.keras.layers.Dense(100 + 1, activation=tf.nn.relu),
        tf.keras.layers.Dense(10, activation='softmax')  # 全连接层
    #                       输出神经元数量  激活函数(softmax)
    ])

隐藏层数和神经元数量非固定的，自己测试之后添加的。

添加隐层前： 

 添加隐层后；

2、设置优化器、损失函数

# 2、设置优化器、损失函数
    model.compile(optimizer=SGD(0.3), loss='mse', metrics=['accuracy'])
    #             优化器     学习率0.3  损失函数(均方误差) 保留标签(accuracy)

目前测试的最佳学习率：0.3（本模型）

3、训练

# 3、训练
    model.fit(train_data, train_label, epochs=20, batch_size=32, validation_data=(test_data, test_label))
#             训练集                    遍历20次    一组32个        测试集

三、预测

1、备份图像数据集

这里准备了2个图像数据集，一份用于后面的预测分类，一份用于显示图像。

为什么不用一份呢？因为两者维度不同，预测的需要更高一维度的数据。 

# 图像增加维度
    Images = images[:, np.newaxis]
    # images图像正常显示，Images图像用来做预测

2、预测分类

# 预测分类
        classification = model.predict(Images[i], batch_size=10)
        # 得到结果
        result.append(np.argmax(classification[0]))

3、显示结果(plt)

# 显示结果
        x = int(i/3)
        y = i%3

        ax[x][y].set_title(f'label:{labels[i]}-predict:{result[i]}')    # 设置标题
        ax[x][y].imshow(images[i], 'gray')                              # 显示图像
        ax[x][y].axis('off')                                            # 隐藏坐标轴

训练1次： 

 训练30次：

训练了30次的情况： 

 D:\Software\Python\Python\python.exe D:/Study/AI/OpenCV/draft.py/main.py
Epoch 1/30
1875/1875 [==============================] - 6s 3ms/step - loss: 0.0393 - accuracy: 0.7064 - val_loss: 0.0114 - val_accuracy: 0.9270
Epoch 2/30
1875/1875 [==============================] - 5s 3ms/step - loss: 0.0105 - accuracy: 0.9310 - val_loss: 0.0075 - val_accuracy: 0.9498
Epoch 3/30
1875/1875 [==============================] - 5s 3ms/step - loss: 0.0072 - accuracy: 0.9538 - val_loss: 0.0062 - val_accuracy: 0.9603
Epoch 4/30
1875/1875 [==============================] - 5s 3ms/step - loss: 0.0057 - accuracy: 0.9635 - val_loss: 0.0055 - val_accuracy: 0.9658
Epoch 5/30
1875/1875 [==============================] - 5s 3ms/step - loss: 0.0047 - accuracy: 0.9703 - val_loss: 0.0048 - val_accuracy: 0.9691
Epoch 6/30
1875/1875 [==============================] - 5s 3ms/step - loss: 0.0040 - accuracy: 0.9746 - val_loss: 0.0048 - val_accuracy: 0.9694
Epoch 7/30
1875/1875 [==============================] - 6s 3ms/step - loss: 0.0034 - accuracy: 0.9787 - val_loss: 0.0049 - val_accuracy: 0.9669
Epoch 8/30
1875/1875 [==============================] - 5s 3ms/step - loss: 0.0030 - accuracy: 0.9816 - val_loss: 0.0043 - val_accuracy: 0.9713
Epoch 9/30
1875/1875 [==============================] - 6s 3ms/step - loss: 0.0026 - accuracy: 0.9844 - val_loss: 0.0038 - val_accuracy: 0.9760
Epoch 10/30
1875/1875 [==============================] - 6s 3ms/step - loss: 0.0023 - accuracy: 0.9864 - val_loss: 0.0050 - val_accuracy: 0.9677
Epoch 11/30
1875/1875 [==============================] - 7s 4ms/step - loss: 0.0021 - accuracy: 0.9873 - val_loss: 0.0037 - val_accuracy: 0.9764
Epoch 12/30
1875/1875 [==============================] - 6s 3ms/step - loss: 0.0018 - accuracy: 0.9894 - val_loss: 0.0037 - val_accuracy: 0.9758
Epoch 13/30
1875/1875 [==============================] - 7s 4ms/step - loss: 0.0017 - accuracy: 0.9901 - val_loss: 0.0041 - val_accuracy: 0.9734
Epoch 14/30
1875/1875 [==============================] - 7s 4ms/step - loss: 0.0015 - accuracy: 0.9911 - val_loss: 0.0045 - val_accuracy: 0.9708
Epoch 15/30
1875/1875 [==============================] - 7s 4ms/step - loss: 0.0014 - accuracy: 0.9921 - val_loss: 0.0038 - val_accuracy: 0.9760
Epoch 16/30
1875/1875 [==============================] - 7s 4ms/step - loss: 0.0013 - accuracy: 0.9922 - val_loss: 0.0036 - val_accuracy: 0.9764
Epoch 17/30
1875/1875 [==============================] - 6s 3ms/step - loss: 0.0012 - accuracy: 0.9932 - val_loss: 0.0035 - val_accuracy: 0.9771
Epoch 18/30
1875/1875 [==============================] - 6s 3ms/step - loss: 0.0011 - accuracy: 0.9942 - val_loss: 0.0034 - val_accuracy: 0.9783
Epoch 19/30
1875/1875 [==============================] - 7s 4ms/step - loss: 9.5588e-04 - accuracy: 0.9947 - val_loss: 0.0034 - val_accuracy: 0.9788
Epoch 20/30
1875/1875 [==============================] - 6s 3ms/step - loss: 9.9405e-04 - accuracy: 0.9942 - val_loss: 0.0037 - val_accuracy: 0.9767
Epoch 21/30
1875/1875 [==============================] - 7s 4ms/step - loss: 8.7466e-04 - accuracy: 0.9952 - val_loss: 0.0037 - val_accuracy: 0.9757
Epoch 22/30
1875/1875 [==============================] - 7s 4ms/step - loss: 7.5603e-04 - accuracy: 0.9959 - val_loss: 0.0037 - val_accuracy: 0.9773
Epoch 23/30
1875/1875 [==============================] - 7s 4ms/step - loss: 7.8775e-04 - accuracy: 0.9955 - val_loss: 0.0035 - val_accuracy: 0.9783
Epoch 24/30
1875/1875 [==============================] - 7s 4ms/step - loss: 7.2748e-04 - accuracy: 0.9961 - val_loss: 0.0034 - val_accuracy: 0.9779
Epoch 25/30
1875/1875 [==============================] - 7s 4ms/step - loss: 7.2780e-04 - accuracy: 0.9959 - val_loss: 0.0036 - val_accuracy: 0.9777
Epoch 26/30
1875/1875 [==============================] - 6s 3ms/step - loss: 5.9373e-04 - accuracy: 0.9969 - val_loss: 0.0032 - val_accuracy: 0.9792
Epoch 27/30
1875/1875 [==============================] - 6s 3ms/step - loss: 5.6153e-04 - accuracy: 0.9970 - val_loss: 0.0034 - val_accuracy: 0.9786
Epoch 28/30
1875/1875 [==============================] - 7s 4ms/step - loss: 5.7011e-04 - accuracy: 0.9969 - val_loss: 0.0033 - val_accuracy: 0.9792
Epoch 29/30
1875/1875 [==============================] - 7s 4ms/step - loss: 5.0371e-04 - accuracy: 0.9973 - val_loss: 0.0037 - val_accuracy: 0.9767
Epoch 30/30
1875/1875 [==============================] - 7s 4ms/step - loss: 5.2224e-04 - accuracy: 0.9972 - val_loss: 0.0033 - val_accuracy: 0.9795

可以发现，训练次数过高，后面变化就已经不大了。 

总代码

# keras手写数字识别
import os
os.environ['TF_CPP_MIN_LOG_LEVEL']='2'

import tensorflow as tf
from tensorflow.keras.optimizers import SGD
import numpy as np
import matplotlib.pyplot as plt

# 数据准备
def Data_Preparation():
    global train_data, train_label, test_data, test_label, mnist_train, \
        mnist_test, images, labels
    # 1、载入数据集
    mnist = tf.keras.datasets.mnist
    (train_data, train_label), (test_data, test_label) = mnist.load_data()
    # 训练集数据 train_data 的数据形状为(60000，28，28)
    # 训练集标签 train_label 的数据形状为(60000)
    # 测试集数据 test_data 的数据形状为(10000，28，28)
    # 测试集标签 test_label 的数据形状为(10000)
    images, labels = test_data, test_label

    # 2、数据处理（归一化、独热编码）
    # 2-1、数据集归一化
    train_data = train_data/255
    test_data = test_data/255

    # 2-2、标签独热编码
    train_label = tf.keras.utils.to_categorical(train_label, num_classes=10)
    test_label = tf.keras.utils.to_categorical(test_label, num_classes=10)
    #                           转化为独热编码   待转数据      独热码长度


# 神经网络拟合
def Neural_Network():
    global model
    # 1、创建神经网络
    model = tf.keras.models.Sequential([
        #
        tf.keras.layers.Flatten(input_shape=(28, 28)),   # 输入数据压缩，三维变二维
        # (60000,28,28) -> (60000, 784)
        tf.keras.layers.Dense(200 + 1, activation=tf.nn.relu),
        tf.keras.layers.Dense(200 + 1, activation=tf.nn.relu),
        tf.keras.layers.Dense(200 + 1, activation=tf.nn.relu),
        tf.keras.layers.Dense(100 + 1, activation=tf.nn.relu),
        tf.keras.layers.Dense(100 + 1, activation=tf.nn.relu),
        tf.keras.layers.Dense(100 + 1, activation=tf.nn.relu),
        tf.keras.layers.Dense(10, activation='softmax')  # 全连接层
    #                       输出神经元数量  激活函数(softmax)
    ])

    # 2、设置优化器、损失函数
    model.compile(optimizer=SGD(0.3), loss='mse', metrics=['accuracy'])
    #             优化器     学习率0.3  损失函数(均方误差) 保留标签(accuracy)

    # 3、训练
    model.fit(train_data, train_label, epochs=20, batch_size=32, validation_data=(test_data, test_label))
#             训练集                    遍历20次    一组32个        测试集


# 预测手写数字（可视化部分测试集的预测）
def Predict():
    global images
    # 预测结果
    result = []
    # plt图表
    f, ax = plt.subplots(3, 3, figsize=(8, 6))

    # 图像增加维度
    Images = images[:, np.newaxis]
    # images图像正常显示，Images图像用来做预测

    # 在测试集中选取一部分数据进行可视化分类
    for i in range(9):
        # 预测分类
        classification = model.predict(Images[i], batch_size=10)
        # 得到结果
        result.append(np.argmax(classification[0]))

        # 显示结果
        x = int(i/3)
        y = i%3

        ax[x][y].set_title(f'label:{labels[i]}-predict:{result[i]}')    # 设置标题
        ax[x][y].imshow(images[i], 'gray')                              # 显示图像
        ax[x][y].axis('off')                                            # 隐藏坐标轴

    plt.show()


# 数据准备
Data_Preparation()
# 神经网络搭建
Neural_Network()
# 手写数字预测
Predict()