数据挖掘---营销推广预测响应

数据集及源码：https://download.csdn.net/download/qq_42363032/12645777

预测

1.读取数据

做预测，所以离散列TARGET_B删除

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

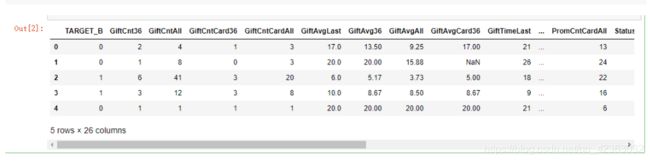
model_data = pd.read_csv("donations2.csv").drop(["ID","TARGET_B"],1)   # 做预测，离散值TARGET_B删除
model_data.head()

2.提取X和Y

做预测，Y是连续型

特征有好多列，既有数值型又有离散型，这里把数值型取出为一组，离散型取出为一组，分别用相关系数和方差分析做特征筛选

print(model_data.dtypes)  # 看一下数据类型
y = ["TARGET_D"]
# 提取X分为数值类型和非数值类型
var_c = ["GiftCnt36","GiftCntAll","GiftCntCard36","GiftCntCardAll","GiftTimeLast",
         "GiftTimeFirst","PromCnt12","PromCnt36","PromCntAll","PromCntCard12",
         "PromCntCard36","PromCntCardAll","StatusCatStarAll","DemAge",
         "DemMedHomeValue","DemPctVeterans","DemMedIncome","GiftAvgLast",
         "GiftAvg36","GiftAvgAll","GiftAvgCard36"]
var_d = ['DemGender', 'StatusCat96NK', 'DemCluster', 'DemHomeOwner']
X = model_data[var_c + var_d]
Y = model_data[y]

3.连续型变量特征重要性筛选（相关系数）

X和Y都是数值型用相关系数

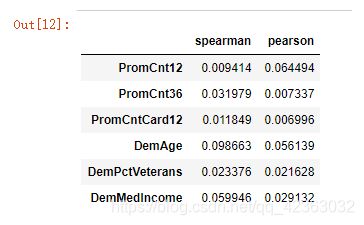
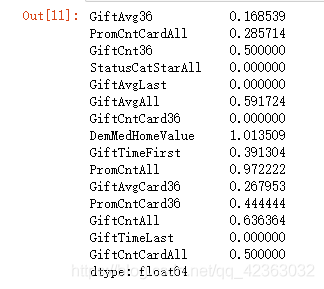
corr_s = abs(model_data[y + var_c].corr(method = 'spearman'))   # spearman：斯皮尔曼相关系数
# print(corr_s['TARGET_D'])
corr_s = pd.DataFrame(corr_s.iloc[0,:])   # 第一列是TARGET_D
corr_p = abs(model_data[y + var_c].corr(method = 'pearson'))   # pearson：皮尔逊相关系数
corr_p = pd.DataFrame(corr_p.iloc[0,:])
corr_sp = pd.concat([corr_s,corr_p], axis = 1)
corr_sp.columns = ['spearman','pearson']
corr_sp

将相关系数小于0.1的删除(弱相关)

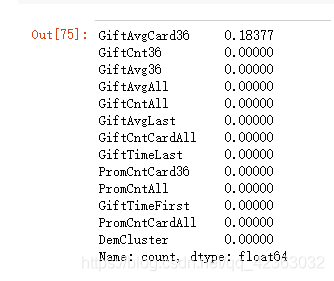
corr_sp[(corr_sp['spearman'] <= 0.1) & (corr_sp['pearson'] <= 0.1)]

筛选之后的数值型特征

var_c_s = set(var_c) - set(['PromCnt12','PromCnt36',
                            'PromCntCard12','DemAge',
                            'DemPctVeterans','DemMedIncome'])   # 集合的差集运算
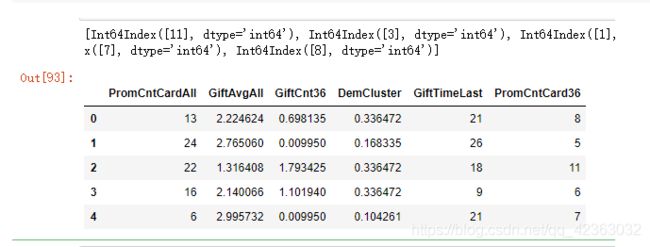
var_c_s = list(var_c_s)
var_c_s

4.离散型变量特征筛选（方差分析）

X和Y既有离散型又有数值型用方差分析

# 当X和Y既有离散值又有连续值，通过方差分析看二者之间关系
# P值大于0.05的，需要删除，这些特征都是没有影响的没有关系的
import statsmodels.stats.anova as anova
from statsmodels.formula.api import ols
for i in var_d:
    formula = "TARGET_D ~ " + str(i)
    print(anova.anova_lm(ols(formula,data = model_data[var_d+['TARGET_D']]).fit()))  # 方差分析是线性方程的特例

P值大于0.05的需要删除，说明此特征对Y没有影响没有关系

筛选之后的离散型特征

var_d_s = list(set(var_d) - set(["DemHomeOwner"]))
var_d_s

5.特征重新拼接

X = model_data[var_c_s + var_d_s].copy()
Y = model_data[y].copy()
model_data[var_c_s+var_d_s].head()

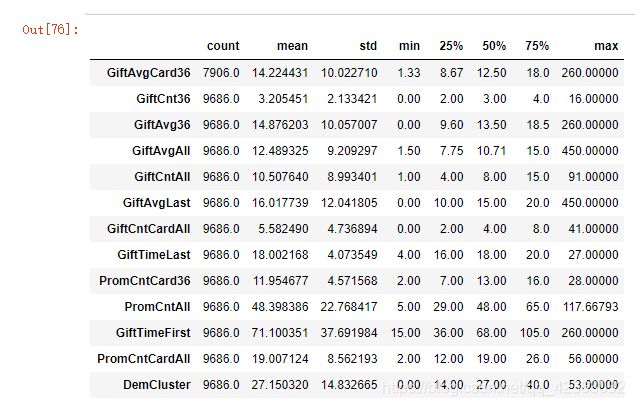
看一下连续型特征的基本统计量（EDA探索性分析）

X[var_c_s].describe().T   # 看一下数值型特征的描述性信息，基本的统计量
# count代表有效值的数量

abs((X[var_c_s].mode().iloc[0,] - X[var_c_s].median()) /
    (X[var_c_s].quantile(0.75) - X[var_c_s].quantile(0.25)))
# （众数 - 中位数）/（上四分位数 - 下四分位数）【极差】
# 如果值大于0.8或者大于1，说明这个数稍微有点偏了，有可能存在异常值

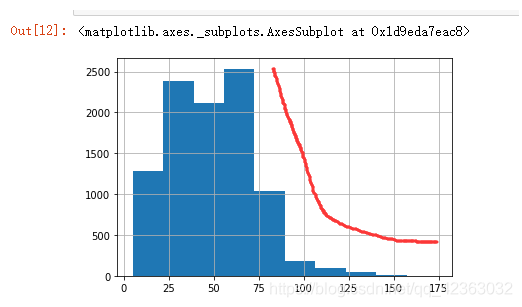
看一下直方图和偏度值

X["PromCntAll"].hist()

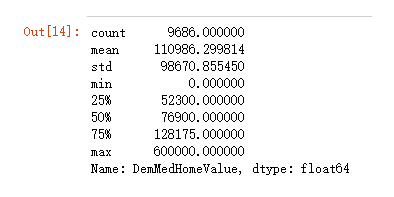
X["DemMedHomeValue"].hist()

X["DemMedHomeValue"].describe().T

X['DemMedHomeValue'].replace(0, np.nan, inplace = True)

说明PromCntAll和DemMedHomeValue需要做对数处理

连续型变量处理

1 - (X.describe().T["count"]) / len(X)

GiftAvgCard36_fill = X["GiftAvgCard36"].median()  # 中位数
DemMedHomeValue_fill = X["DemMedHomeValue"].median()
X["GiftAvgCard36"].fillna(GiftAvgCard36_fill,inplace = True)  # 用中位数进行缺失值填充
X["DemMedHomeValue"].fillna(DemMedHomeValue_fill,inplace = True)
skew_var_x = {
     }
for i in var_c_s:
    skew_var_x[i]=abs(X[i].skew())   # 看一下峰值  
skew = pd.Series(skew_var_x).sort_values(ascending=False)
skew

var_x_ln = skew[skew >= 1].index  #返回大于等于1的索引
var_x_ln

对数处理

# 对数处理
for i in var_x_ln:
    if min(X[i]) <= 0:
        X[i] = np.log(X[i] + abs(min(X[i])) + 0.01)
    else:
        X[i] = np.log(X[i])

# 看一下峰值
skew_var_x = {
     }
for i in var_c_s:
    skew_var_x[i]=abs(X[i].skew())

skew = pd.Series(skew_var_x).sort_values(ascending=False)
skew

看一下离散型特征的基本统计量（EDA探索性分析）

对于离散型的变量没有办法算统计量，一般情况做一下频数分布的计算

类别数一般6-8类就是比较不错的

X["DemGender"].value_counts()  # 这个特征只有3类，还可以

X["StatusCat96NK"].value_counts() #有的水平数量太少，需要合并，类别少的归成一类

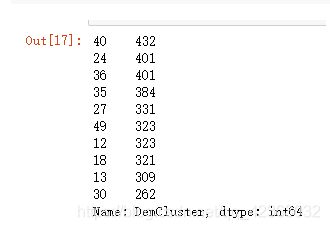
X["DemCluster"].value_counts()[:10]  # 这个类别太多，好像50多个，也需要合并，比如合并到8-10类

离散型变量处理

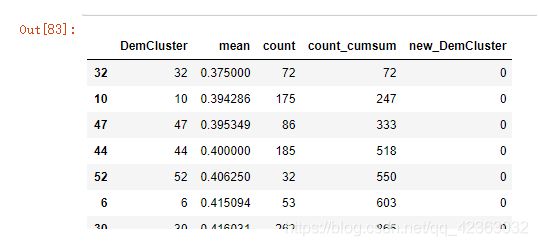
对于DemCluster

# as_index 的默认值为True， 对于聚合输出，返回以组标签作为索引的对象。仅与DataFrame输入相关。as_index = False实际上是“SQL风格”的分组输出
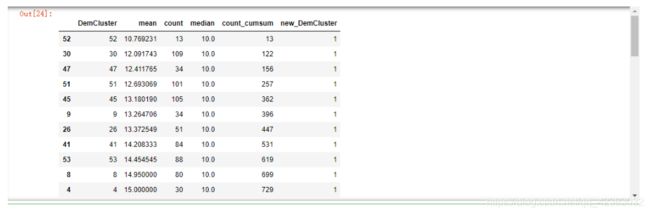
DemC_group = model_data[['DemCluster','TARGET_D']].groupby('DemCluster',as_index = False)
DemC_C= DemC_group['TARGET_D'].agg({
     'mean' : 'mean','count':'count',"median":"median"}).sort_values(["median","mean"])
DemC_C["count_cumsum"] = DemC_C["count"].cumsum()
DemC_C["new_DemCluster"] = DemC_C["count_cumsum"].apply(lambda x:x//(len(model_data)/10)+1)
DemC_C["new_DemCluster"] = DemC_C["new_DemCluster"].astype(int)
DemC_C

len(model_data)

DemCluster_new_class = DemC_C[["DemCluster","new_DemCluster"]].set_index("DemCluster")
X["DemCluster"] = X["DemCluster"].map(DemCluster_new_class.to_dict()['new_DemCluster'])
new_DemGender = {
     "F":1,"M":2,"U":3}
X['DemGender'] = X['DemGender'].map(new_DemGender)

对于StatusCat96NK

StatusCat96NK_group = model_data[['StatusCat96NK','TARGET_D']].groupby('StatusCat96NK', as_index = False)
StatusCat96NK_class = StatusCat96NK_group['TARGET_D'].agg({
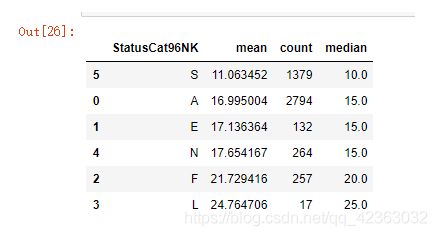
     'mean' : 'mean', 'count':'count',"median":"median"}).sort_values(["median","mean"])
StatusCat96NK_class

new_StatusCat96NK = {
     "S":1,"A":2,"E":2,"N":2,"F":2,"L":2}
X['StatusCat96NK'] = X['StatusCat96NK'].map(new_StatusCat96NK)
X.head()

6.前向选择法筛选变量

import statsmodels.formula.api as smf
def forward_selected(data, response):
    remaining = set(data.columns)
    remaining.remove(response)
    selected = []
    current_score, best_new_score = 0.0, 0.0
    while remaining and current_score == best_new_score:
        scores_with_candidates = []
        for candidate in remaining:
            formula = "{} ~ {} + 1".format(response,
                                           ' + '.join(selected + [candidate]))
            score = smf.ols(formula, data).fit().rsquared_adj
            scores_with_candidates.append((score, candidate))
        scores_with_candidates.sort()
        best_new_score, best_candidate = scores_with_candidates.pop()
        if current_score < best_new_score:
            remaining.remove(best_candidate)
            selected.append(best_candidate)
            current_score = best_new_score
    formula = "{} ~ {} + 1".format(response,
                                   ' + '.join(selected))
    model = smf.ols(formula, data).fit()
    return selected

XX=pd.concat([X[var_c_s+var_d_s],Y],axis = 1)

final_var = forward_selected(XX,'TARGET_D')

var_c_s = list(set(var_c_s)&set(final_var))
var_c_s

var_d_s = list(set(var_d_s)&set(final_var))
var_d_s

model_final = pd.concat([X[var_d_s + var_c_s],Y], axis = 1)
model_final.columns

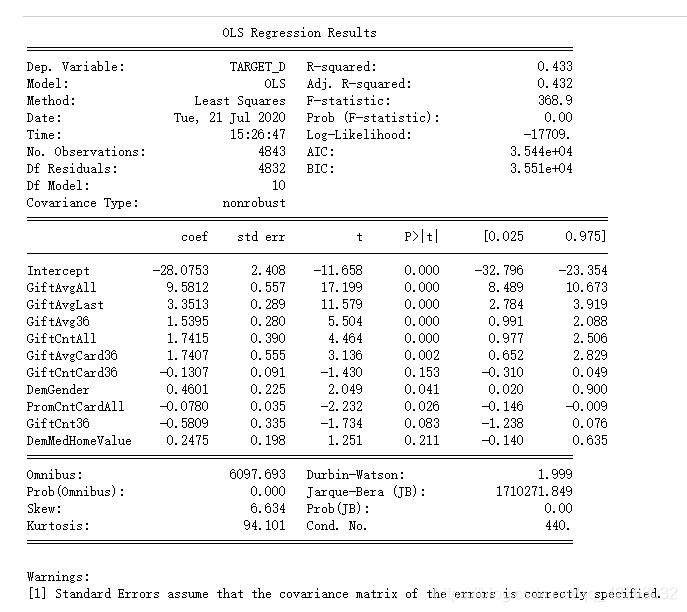
7.建立线性回归模型

import statsmodels.api as sm
from statsmodels.formula.api import ols
X = model_final.iloc[:,:-1]
Y = model_final.iloc[:,-1]
formula = 'TARGET_D ~ ' + '+'.join(final_var) 
donation_model = ols(formula,model_final).fit()
print(donation_model.summary())

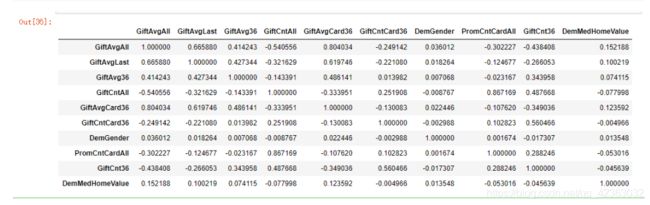
model_final[final_var].corr()

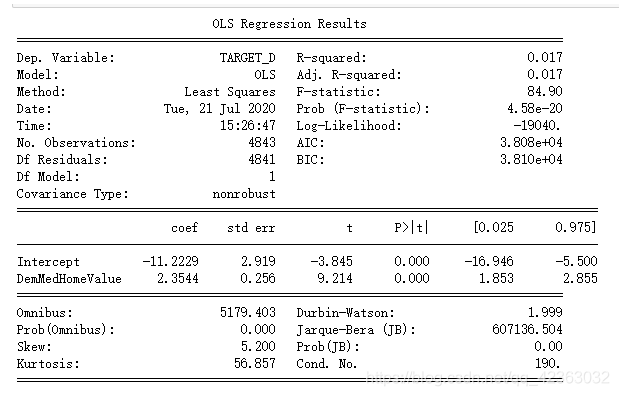
用DemMedHomeValue做线性回归模型看一下结果

formula = 'TARGET_D ~ DemMedHomeValue' 
model = ols(formula,model_final).fit()
print(model.summary())

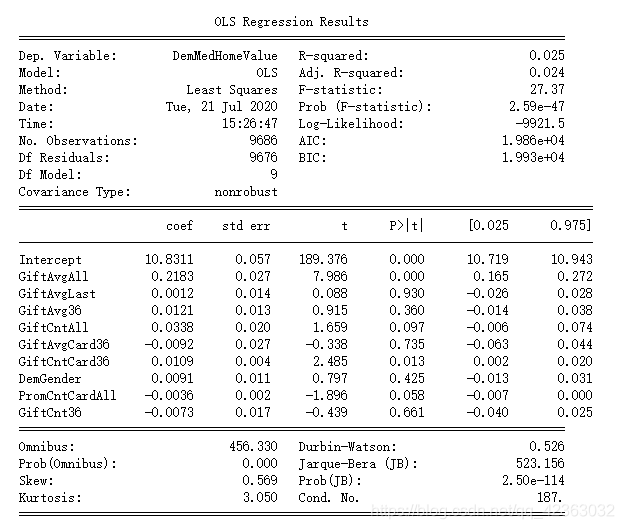
看一下特征共线性

final_varN = ['GiftAvgAll',
 'GiftAvgLast',
 'GiftAvg36',
 'GiftCntAll',
 'GiftAvgCard36',
 'GiftCntCard36',
 'DemGender',
 'PromCntCardAll',
 'GiftCnt36']

formula = 'DemMedHomeValue ~ ' + '+'.join(final_varN) 
model = ols(formula,model_final).fit()
print(model.summary())

formula = 'TARGET_D ~ ' + '+'.join(final_varN) 
model = ols(formula,model_final).fit()
print(model.summary())

回归

1.读入数据

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

# ID TARGET_D 删除这两列
model_data=pd.read_csv("donations2.csv").drop(["ID","TARGET_D"],1)
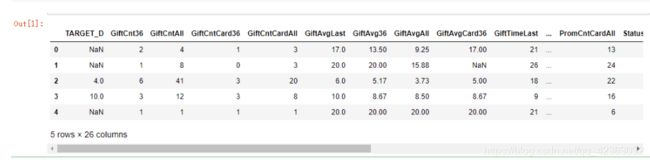
model_data.head()

一个经验的做法，对特征去重，根据去重后的个数是否大于10，来判断特征是数值型还是离散型

比如，判断GiftCntAll这一列是数值型还是离散型

len(model_data['GiftCntAll'].drop_duplicates())     # 69，大于10，说明是数值型

model_data.dtypes
y = 'TARGET_B'
# 数值类型
var_c = ["GiftCnt36","GiftCntAll","GiftCntCard36",
         "GiftCntCardAll","GiftTimeLast","GiftTimeFirst",
         "PromCnt12","PromCnt36","PromCntAll",
         "PromCntCard12","PromCntCard36","PromCntCardAll",
         "StatusCatStarAll","DemAge","DemMedHomeValue",
         "DemPctVeterans","DemMedIncome","GiftAvgLast",
         "GiftAvg36","GiftAvgAll","GiftAvgCard36"]
# 类别类型
var_d = ['StatusCat96NK', 'DemHomeOwner', 'DemGender', 'DemCluster']
X = model_data[var_c + var_d].copy()
Y = model_data[y].copy()

2.特征筛选（卡方检验）

当Y和X都是离散型时，用卡方检验做特征筛选

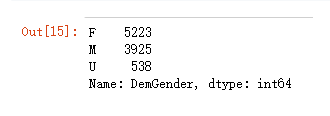
以DemGender列为例

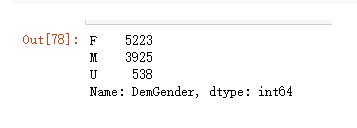
先看一下频数统计

model_data['DemGender'].value_counts()

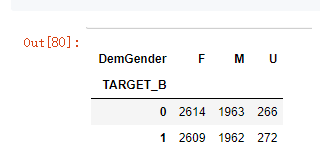
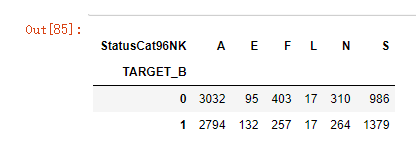
看一下列联交叉表

# 非参数统计------------------列联交叉表
cross = pd.crosstab(model_data['TARGET_B'],model_data['DemGender'])
cross

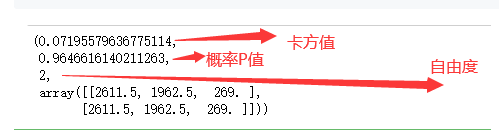
用这个列联交叉表做这个特征的卡方检验

from scipy import stats
from pprint import pprint
pprint(stats.chi2_contingency(cross))   # 卡方值、概率P值、自由度

DemGender列的概率P值是大于0.05的，所以是需要删除的，它对结果没有影响

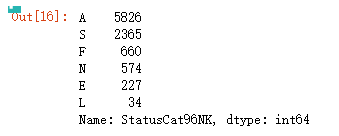
以StatusCat96NK列为例

频数统计

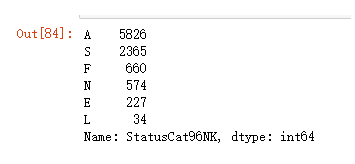
model_data['StatusCat96NK'].value_counts()

列联交叉

# 非参数统计------------------列联交叉表
cross = pd.crosstab(model_data['TARGET_B'],model_data['StatusCat96NK'])
cross

卡方检验

from scipy import stats
from pprint import pprint
pprint(stats.chi2_contingency(cross))   # 卡方值、概率P值、自由度

3.通过WOE、IV看一下特征筛选

底层实现

def CalcWOE(df, col, target):
    '''
    :param df: 包含需要计算WOE的变量和目标变量
    :param col: 需要计算WOE、IV的变量，必须是分箱后的变量，或者不需要分箱的类别型变量，也就是离散型
    :param target: 目标变量，0、1表示好、坏
    :return: 返回WOE和IV
    '''
    total = df.groupby([col])[target].count()   # 对col列根据类别标签做一下分组统计，求的是每个col标签的样本总数
    total = pd.DataFrame({
     'total': total})      # 下面需要做表关联，转换成数据框
    bad = df.groupby([col])[target].sum()      # 每个col标签的坏样本总数(1的)
    bad = pd.DataFrame({
     'bad': bad})
    regroup = total.merge(bad, left_index=True, right_index=True, how='left')
    regroup.reset_index(level=0, inplace=True)   # 索引重置
    N = sum(regroup['total'])
    B = sum(regroup['bad'])
    regroup['good'] = regroup['total'] - regroup['bad']   # 好样本数
    G = N - B
    regroup['bad_pcnt'] = regroup['bad'].map(lambda x: x*1.0/B)   # 坏样本率
    regroup['good_pcnt'] = regroup['good'].map(lambda x: x * 1.0 / G)   # 好样本率
    
    regroup['WOE'] = regroup.apply(lambda x: np.log(x.good_pcnt*1.0/x.bad_pcnt),axis = 1)
    WOE_dict = regroup[[col,'WOE']].set_index(col).to_dict(orient='index')
    for k, v in WOE_dict.items():
        WOE_dict[k] = v['WOE']
    IV = regroup.apply(lambda x: (x.good_pcnt-x.bad_pcnt)*np.log(x.good_pcnt*1.0/x.bad_pcnt),axis = 1)
    IV = sum(IV)
    return {
     "WOE": WOE_dict, 'IV':IV}

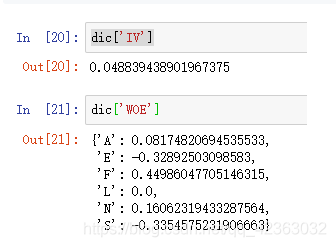
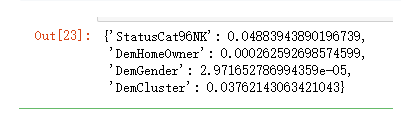
dic = CalcWOE(model_data, 'StatusCat96NK', 'TARGET_B')
dic['IV']
dic['WOE']

一般来说某个特征的IV值大于0.02,越大越好，越大说明特征越重要，可以理解随机森林的特征重要度等价

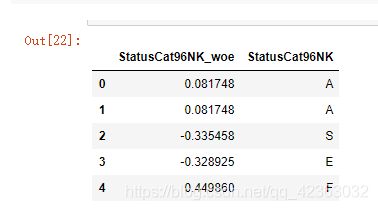
WOE入摸

model_data['StatusCat96NK_woe'] = model_data['StatusCat96NK'].map(dic['WOE'])
model_data[['StatusCat96NK_woe','StatusCat96NK']].head()

调包实现

from woe import WoE
iv_d = {
     }
for i in var_d:
    iv_d[i] = WoE(v_type='d').fit(X[i].copy(), Y.copy()).iv
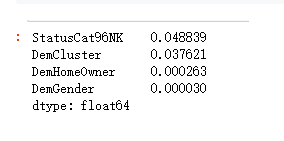
iv_d

根据IV值筛选离散变量

from woe import WoE
iv_d = {
     }
for i in var_d:
    iv_d[i] = WoE(v_type='d').fit(X[i].copy(), Y.copy()).iv   # 参数是离散型 v_type=‘d’
iv_d

pd.Series(iv_d).sort_values(ascending = False)

var_d_s = ['StatusCat96NK', 'DemCluster']

根据IV值筛选连续型变量

iv_c = {
     }
for i in var_c:
    iv_c[i] = WoE(v_type='c',t_type='b',qnt_num=3).fit(X[i],Y).iv   # 参数是数值型 v_type=‘c’
sort_iv_c = pd.Series(iv_c).sort_values(ascending=False)
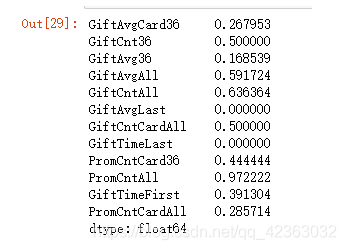
sort_iv_c

保留iv值大于0.02的

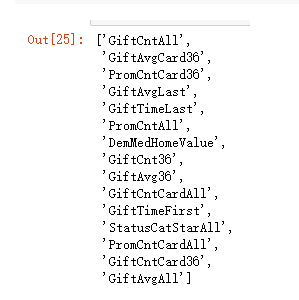
var_c_s = list(sort_iv_c[sort_iv_c > 0.02].index)
var_c_s

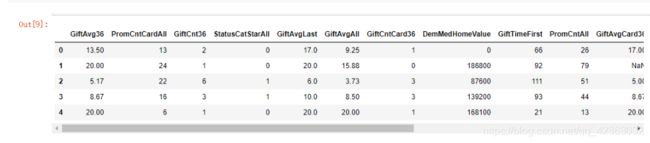
X = model_data[var_c_s + var_d_s].copy()
Y = model_data[y].copy()
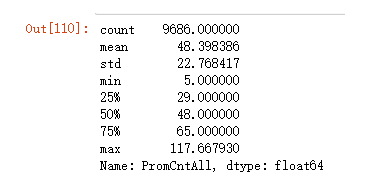
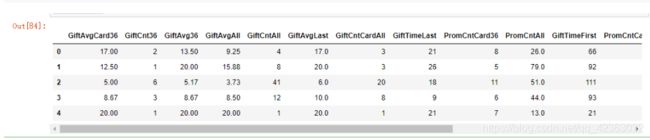
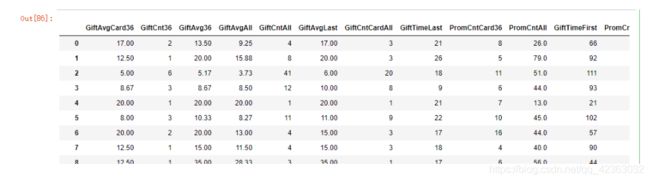
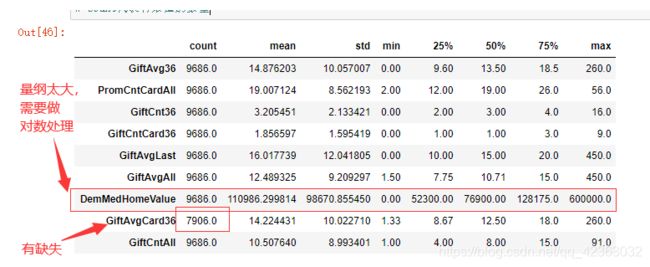
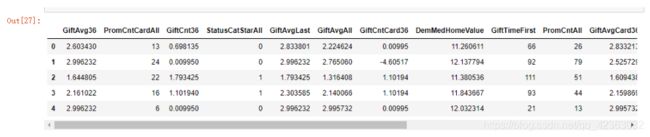
X[var_c_s].describe().T

4.EDA探索性分析

就是描述性统计加可视化

（众数 - 中位数）/（分位数极差）

经验来看，一般这个值大于0.8，说明它有偏，画一下直方图看看

abs((X[var_c_s].mode().iloc[0,] - X[var_c_s].median()) /
    (X[var_c_s].quantile(0.75) - X[var_c_s].quantile(0.25)))

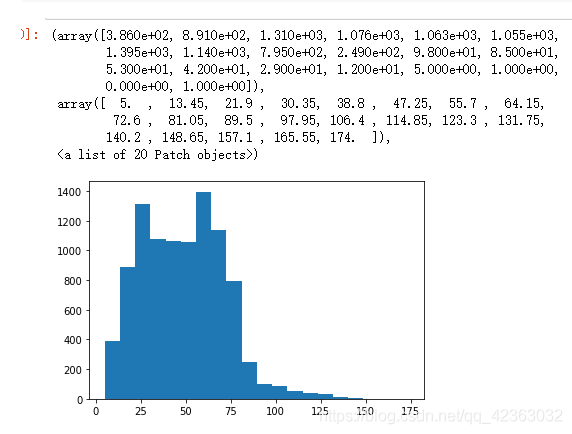
plt.hist(X["PromCntAll"], bins=20)

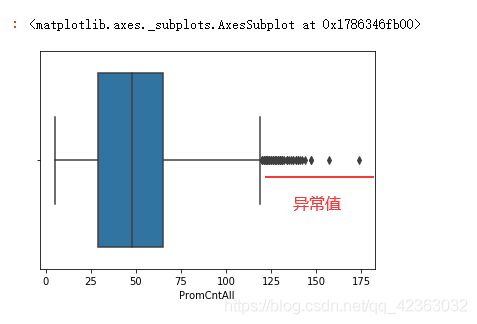
柱形图右面偏离是异常值

# 箱线图
# 上边缘的计算方法是 上四分位数+1.5倍极差
import seaborn as sns
sns.boxplot(X["PromCntAll"])

消除异常值

1.均值加减三倍标准差，盖帽法替换

prc_mean = X["PromCntAll"].mean()
prc_std = X["PromCntAll"].std()
high = prc_mean + 3*prc_std
low = prc_mean - 3*prc_std
def s(x):
    if x > high:
        return high
    elif x < low:
        return low
    else:
        return x

2.计算百分数

# 计算百分位数
p1 = X["PromCntAll"].quantile(0.01)   
p99 = X["PromCntAll"].quantile(0.99)   
print(p1)
print(p99)

用均值加减三倍标准差消除异常值

X["PromCntAll"] = X["PromCntAll"].map(s)
X["PromCntAll"].describe()

X["PromCntAll"][X["PromCntAll"] > low][X["PromCntAll"] < high].describe()

5.针对有问题的变量进行修改

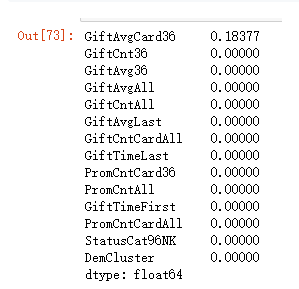
1 - X.count()/ len(X)

X.isnull().sum()/len(X)

1 - (X.describe().T["count"]) / len(X)

X.describe().T

连续型变量修改

fill_GiftAvgCard36 = X.GiftAvgCard36.median()
X.GiftAvgCard36.fillna(value=fill_GiftAvgCard36, inplace=True)

X.GiftAvgCard36.fillna(method='ffill', inplace=True)

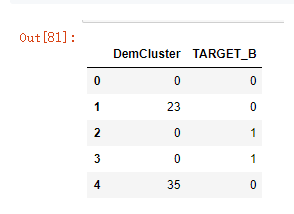
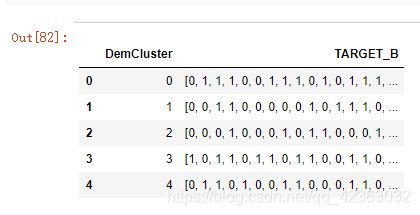
model_data[['DemCluster','TARGET_B']].head()

model_data[['DemCluster','TARGET_B']].groupby('DemCluster',as_index = False).agg(list).head()

离散型变量修改

# 统计每个水平的对应目标变量的均值，和每个水平数量

DemCluster_grp = model_data[['DemCluster',
                             'TARGET_B']].groupby('DemCluster',as_index = False)

DemC_C = DemCluster_grp['TARGET_B'].agg({
     'mean' : 'mean',
                                                   'count':'count'}).sort_values("mean")

# 将这些类别尽量以人数大致均等的方式以响应率为序归结为10个大类
DemC_C["count_cumsum"] = DemC_C["count"].cumsum()
DemC_C["new_DemCluster"] = DemC_C["count_cumsum"].apply(lambda x: x//(len(model_data)/10)).astype(int)
DemC_C

X_rep = X.copy()
for i in var_d_s:
    X_rep[i+"_woe"] = WoE(v_type='d').fit_transform(X_rep[i],Y)
X_rep.head()

StatusCat96NK_woe = X_rep[["StatusCat96NK","StatusCat96NK_woe"]].drop_duplicates().set_index("StatusCat96NK").to_dict()
StatusCat96NK_woe

StatusCat96NK_woe = X_rep[["StatusCat96NK","StatusCat96NK_woe"]].drop_duplicates().set_index("StatusCat96NK").to_dict()
DemCluster_woe = X_rep[["DemCluster","DemCluster_woe"]].drop_duplicates().set_index("DemCluster").to_dict()
del X_rep["StatusCat96NK"]
del X_rep["DemCluster"]
X_rep.rename(columns={
     "StatusCat96NK_woe":"StatusCat96NK","DemCluster_woe":"DemCluster"},inplace=True)
X_rep

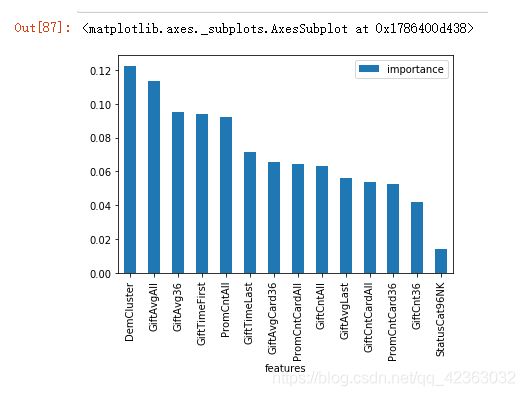
6.通过随机森林对变量的重要性进行筛选

import sklearn.ensemble as ensemble
rfc = ensemble.RandomForestClassifier(criterion='entropy', n_estimators=3, max_features=0.5, min_samples_split=5)
rfc_model = rfc.fit(X_rep, Y)
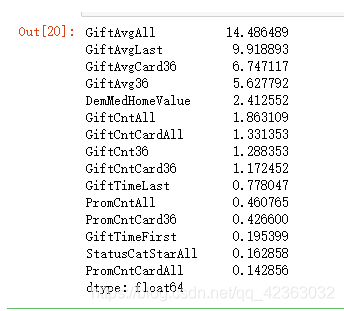
rfc_model.feature_importances_
rfc_fi = pd.DataFrame()
rfc_fi["features"] = list(X.columns)
rfc_fi["importance"] = list(rfc_model.feature_importances_)
rfc_fi=rfc_fi.set_index("features",drop=True)
var_sort = rfc_fi.sort_values(by="importance",ascending=False)
var_sort.plot(kind="bar")

7.变量聚类

每一类选一个具有代表性的

权重向量稀疏解的一个计算

from VarSelec import Var_Select,Var_Select_auto
X_rep_reduc = Var_Select_auto(X_rep)
X_rep_reduc.head()

list(X_rep_reduc.columns)

8.逻辑回归建模

import sklearn.model_selection as model_selection
ml_data = model_selection.train_test_split(X_rep_reduc, Y, test_size=0.3, random_state=0)
train_data, test_data, train_target, test_target = ml_data
from sklearn import preprocessing
min_max_scaler = preprocessing.MinMaxScaler()
train_data = min_max_scaler.fit_transform(train_data)
test_data = min_max_scaler.fit_transform(test_data)
train_data

import sklearn.linear_model as linear_model
logistic_model = linear_model.LogisticRegression(class_weight = None,
                                                 dual = False,
                                                 fit_intercept = True,
                                                 intercept_scaling = 1,
                                                 penalty = 'l2',
                                                 random_state = None,
                                                 tol = 0.001)

from sklearn.model_selection import ParameterGrid, GridSearchCV
C = np.logspace(-3,0,20,base=10)
param_grid = {
     'C': C}
clf_cv = GridSearchCV(estimator=logistic_model, 
                      param_grid=param_grid, 
                      cv=5, 
                      scoring='roc_auc')
clf_cv.fit(train_data, train_target)

import statsmodels.api as sm
import statsmodels.formula.api as smf
model=X_rep_reduc.join(train_target)
formula = "TARGET_B ~ " + "+".join(X_rep_reduc)
lg_m = smf.glm(formula=formula, data=model, family=sm.families.Binomial(sm.families.links.logit)).fit()
lg_m.summary()

9.ROC曲线

test_est = logistic_model.predict(test_data)
train_est = logistic_model.predict(train_data)
test_est_p = logistic_model.predict_proba(test_data)[:,1]
train_est_p = logistic_model.predict_proba(train_data)[:,1]
import sklearn.metrics as metrics
fpr_test, tpr_test, th_test = metrics.roc_curve(test_target, test_est_p)
fpr_train, tpr_train, th_train = metrics.roc_curve(train_target, train_est_p)
plt.figure(figsize=[6,6])
plt.plot(fpr_test, tpr_test)
plt.plot(fpr_train, tpr_train)
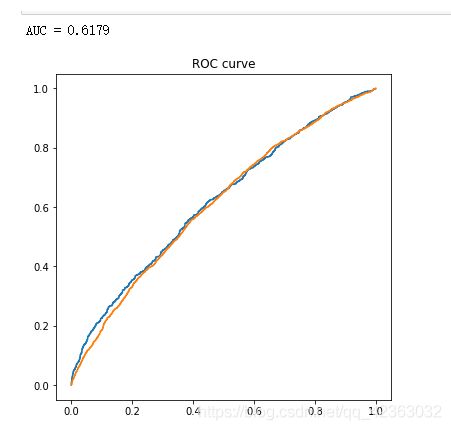
plt.title('ROC curve')
print('AUC = %6.4f' %metrics.auc(fpr_test, tpr_test))