2020.6.29 概率统计-Task04-方差分析

概率统计的最后一节内容，有关方差分析的介绍。Datawhale的课件讲F检验的推导过程讲解的十分详细。在模型实现方面，只给出了R语言的实现途径。笔者将结合另外一个例子，介绍SPSS对于方差分析的实现过程，并对方差分析种类的介绍进行扩展，后期会补充python的实现。

一、概要

1 从独立样本t检验到方差分析

首先举个例子：

1. 如果你的数学成绩和班里的小王差了1分，那么你和小王的分数有没有很大的差异呢？
2. 你们班和隔壁班的数学平均成绩差了1分，那么两个班的水平有没有很大的差异呢？
3. 你们省和隔壁省，用的一套卷子，数学平均分差了1分

因此，当总体很大的情况下，我们就需要一个固定且客观的标准用以判断两个群体的数值是否有差异，而不是主观臆断。在这一背景下，t检验被发明了出来。

• 1 + 2：单样本t检验——一批样本和一个固定的数值，其他数据也是和1比较
• 2 + 3：独立样本t检验——独立的两批人，4 + 5也是独立样本t检验
• 2 + 4：配对样本t检验——配对的数据，3 + 5也是独立样本t检验

但是，独立样本t检验有其局限性，每次只能确定两组是否存在差异，因此，就需要引入方差分析

2 方差分析定义与分类

方差分析(Analysis of variance, ANOVA) 主要研究分类变量作为自变量时，对因变量的影响是否是显著的。

方差分析的方法是由20世纪的统计学家Ronald Aylmer Fisher在1918年到1925年之间提出并陆续完善起来的，该方法刚开始是用于解决田间实验的数据分析问题，因此，方差分析的学习是和实验设计、实验数据的分析密不可分的。

实验设计和方差分析都有自己相应的语言。因此，在这里我们通过一个焦虑症治疗的实例，先了解一些术语，并且思考一下，方差分析主要用于解决什么样的问题。

以焦虑症治疗为例，现有两种治疗方案：认知行为疗法（CBT）和眼动脱敏再加工法（EMDR）。我们招募10位焦虑症患者作为志愿者，随机分配一半的人接受为期五周的CBT，另外一半接受为期五周的EMDR，设计方案如表1-1所示。在治疗结束时，要求每位患者都填写状态特质焦虑问卷（STAI），也就是一份焦虑度测量的自我评测报告。

表1-1 单因素组件方差分析

CBT	EMDR
s1	s4
s2	s5
s3	s6

在这个实验设计中，治疗方案是两水平（CBT、EMDR）的组间因子。之所以称其为组间因子，是因为每位患者都仅被分配到一个组别中，没有患者同时接受CBT和EMDR。表中字母s代表受试者（患者）。STAI是因变量，治疗方案是自变量。由于在每种治疗方案下观测数相等，因此这种设计也称为均衡设计（balanced design）；若观测数不同，则称作非均衡设计（unbalanced design）。

因为仅有一个类别型变量，表1的统计设计又称为单因素方差分析（one-way ANOVA），或进一步称为单因素组间方差分析。方差分析主要通过F检验来进行效果评测，若治疗方案的F检验显著，则说明五周后两种疗法的STAI得分均值不同。

假设你只对CBT的效果感兴趣，则需将10个患者都放在CBT组中，然后在治疗五周和六个月后分别评价疗效，设计方案如表1-2所示。

表1-2 单因素组内方差分析

	时间
患者	5周	6个月
s1
s2
s3
s4
s5
s6

此时，时间（time）是两水平（五周、六个月）的组内因子。因为每位患者在所有水平下都进行了测量，所以这种统计设计称单因素组内方差分析；又由于每个受试者都不止一次被测量，也称作重复测量方差分析。当时间的F检验显著时，说明患者的STAI得分均值在五周和六个月间发生了改变。

现假设你对治疗方案差异和它随时间的改变都感兴趣，则将两个设计结合起来即可：随机分配五位患者到CBT，另外五位到EMDR，在五周和六个月后分别评价他们的STAI结果（见表1-3）。

表1-3 含组间和组内因子的双因素方差分析

		时间
疗法	患者	5周	6个月
CBT	s1
	s2
	s3
EMDR	s4
	s5
	s6

疗法（therapy）和时间（time）都作为因子时，我们既可分析疗法的影响（时间跨度上的平均）和时间的影响（疗法类型跨度上的平均），又可分析疗法和时间的交互影响。前两个称作主效应，交互部分称作交互效应。

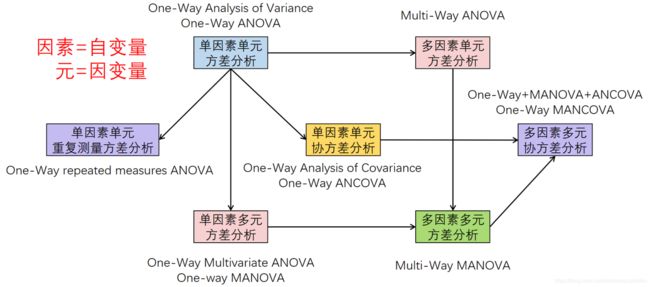
当设计包含两个甚至更多的因子时，便是因素方差分析设计，比如两因子时称作双因素方差分析，三因子时称作三因素方差分析，以此类推。若因子设计包括组内和组间因子，又称作混合模型方差分析，当前的例子就是典型的双因素混合模型方差分析。

本例中，你将做三次F检验：疗法因素一次，时间因素一次，两者交互因素一次。若疗法结果显著，说明CBT和EMDR对焦虑症的治疗效果不同；若时间结果显著，说明焦虑度从五周到六个月发生了变化；若两者交互效应显著，说明两种疗法随着时间变化对焦虑症治疗影响不同（也就是说，焦虑度从五周到六个月的改变程度在两种疗法间是不同的）。

现在，我们对上面的实验设计稍微做些扩展。众所周知，抑郁症对病症治疗有影响，而且抑郁症和焦虑症常常同时出现。即使受试者被随机分配到不同的治疗方案中，在研究开始时，两组疗法中的患者抑郁水平就可能不同，任何治疗后的差异都有可能是最初的抑郁水平不同导致的，而不是由于实验的操作问题。抑郁症也可以解释因变量的组间差异，因此它常称为混淆因素（confounding factor）。由于你对抑郁症不感兴趣，它也被称作干扰变数（nuisance variable）。

假设招募患者时使用抑郁症的自我评测报告，比如白氏抑郁症量表（BDI），记录了他们的抑郁水平，那么你可以在评测疗法类型的影响前，对任何抑郁水平的组间差异进行统计性调整。本案例中，BDI为协变量，该设计为协方差分析（ANCOVA）。

以上设计只记录了单个因变量情况（STAI），为增强研究的有效性，可以对焦虑症进行其他的测量（比如家庭评分、医师评分，以及焦虑症对日常行为的影响评价）。当因变量不止一个时，设计被称作多元方差分析（MANOVA）， 若协变量也存在， 那么就叫多元协方差分析（MANCOVA）。

在此基础上，我们通过另外一个更为直观的例子来了解这些不同的种类

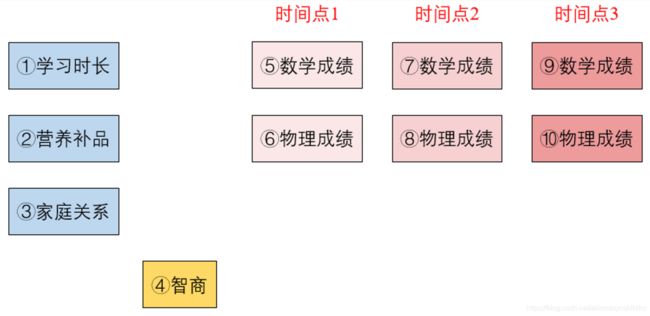
1. ①+⑤：单因素方差分析（One-Way Analysis of Variance，One-Way ANOVA）
2. ①+⑤+⑦+⑨：单因素重复测量方差分析（One-Way repeated measures ANOVA）
3. ①+②+⑤：两因素方差分析（Two-Way ANOVA）
   还可以四因素、五因素、六因素，统称为多因素方差分析（Multi-way ANOVA）
4. ①+②+⑤+⑦+⑨：两因素重复测量方差分析（Two-Way Repeated Measures ANOVA）
5. ①+④+⑤：协方差分析（Analysis of Covariance，ANCOVA）
   为啥①+②+⑤叫做两因素方差分析，把②换成④，就成了协方差分析呢？②是影响因素，④也是影响因素啊！ 解释：因为协变量往往是和自变量有着很高相关性的变量，它并不是我们试验研究的重点，我们只是把它当作控制变量来处理
   协变量（covariate）也是自变量的一种
6. ①+⑤+⑥：多元方差分析（Multivariate ANOVA，MANOVA）
   多因素方差分析：Multi-way
   多元方差分析：Multivariate

二、单因素方差分析

1 推导过程

接下来我们使用种小麦的例子，去帮助理解方差分析里涉及的一些变量。

假设我们现在有若干品种的小麦，要在某一地区播种，我们想知道这些品种的产量有没有显著区别，为此我们先设计了一个田间实验，取一大块地将其分成形状大小都相同的$n$小块．设供选择的品种有$k$个，我们打算其中的$n_1$小块种植品种1, $n_2$小块种植品种2，等等，$n_1+n_2+...n_k=n$.

接下来，我们使用方差分析的方法去看不同小麦品种的产量是否有显著差异。

设问题中涉及一个因素$A$，有$k$个水平，如上例的$k$个种子品种，以$Y_{ij}$记第$i$个水平的第$j$个观察值，如上例$Y_{ij}$是种植品种$i$的第$j$小块地上的亩产量。模型为
$$Y_{ij}=a_i+e_{ij},j=1,...,n_i,i=1,...,k(2.1)$$
$a_i$表示水平$i$的理论平均值，称为水平$i$的效应。在小麦例子中，$a_i$就是品种$i$的平均亩产量，$e_{ij}$就是随机误差。并且我们假定：
$$E(e_{ij})=0,0<Var(e_{ij})={\sigma }^2<\infty ,一切e_{ij}独立同分布(2.2)$$
因素$A$的各水平的高低优劣，取决于其理论平均$a_i$的大小。故对模型(2.1)，我们头一个关心的事情，就是诸$a_i$是否全相同。 如果是，则表示因素$A$对所考察的指标$Y$其实无影响．这时我们就说因素A的效应不显著，否则就说它显著。当然，在实际应用中，所谓“显著”，是指诸$a_i$之间的差异要大到一定的程度．这个 “一定的程度”，是从其实用上的意义着眼，而“统计显著性”，则是与随机误差相比而言．这点在下文的讨论中会有所体现．我们把所要检验的假设写为：
$$H_0:a_1=a_2=\cdots =a_k(2.3)$$
为检验该假设，我们需要分析，为什么各个$Y_{ij}$会有差异？从模型(2.1)来看，无非两个原因：一是各$a_i$可能有差异．例如，若 $a_1>a_2$, 这就使$Y_{1j}$倾向于大于$Y_{2j}$；二是随机误差的存在。这一分析启发了如下的想法：找一个衡量全部$y_{ij}$的变异的量：
$$SS=\sum _{i=1}^k\sum _{j=1}^{n_i}{\left(Y_{ij}-\bar{Y}\right)}^2,\bar{Y}=\sum _{i=1}^k\sum _{j=1}^{n_i}{Y}_{ij}/n(2.4)$$
$SS$愈大，表示$Y_{ij}$之间的差异越大。

接下来，把$SS$分为两部分，一部分表示随机误差的影响，记为$S{S}_e$；另一部分表示因素$A$的各水平理论平均值$a_i$不同带来的影响，记为$S{S}_A$。

关于$S{S}_e$，先固定一个$i$，此时对应的所有观测值$Y_{i1},Y_{i2},\cdots ,Y_{in}$，他们之间的差异与每个水平的理论平均值不等无关，而是取决于随机误差，反映这些观察值差异程度的量是${\sum }_{j=1}^{n_i}{\left(Y_{ij}-\overline{Y_i}\right)}^2$，其中
$$\overline{Y_i}=(Y_{i1}+Y_{i2}+\cdots +Y_{in})/n_i,i=1,2,\cdots ,n(2.5)$$
$\overline{Y_i}$可以视为对$a_i$的估计。把上述平方和做累加得：
$$S{S}_e=\sum _{i=1}^k\sum _{j=1}^{n_i}{\left(Y_{ij}-\overline{Y_i}\right)}^2(2.6)$$
可求得$S{S}_A$:
$$\begin{array}{rl}S{S}_A& =SS-S{S}_e\\ & =\sum _{i=1}^k\sum _{j=1}^{n_i}{\left(Y_{ij}-\bar{Y}\right)}^2-\sum _{i=1}^k\sum _{j=1}^{n_i}{\left(Y_{ij}-\overline{Y_i}\right)}^2\\ & =\sum _{i=1}^k\sum _{j=1}^{n_i}{\left((Y_{ij}-\overline{Y_i})-(\overline{Y_i}-\bar{Y})\right)}^2-\sum _{i=1}^k\sum _{j=1}^{n_i}{\left(Y_{ij}-\overline{Y_i}\right)}^2\\ & =\sum _{i=1}^k\sum _{j=1}^{n_i}\left((Y_{ij}-\overline{Y_i}{)}^2-2(Y_{ij}-\overline{Y_i})(\overline{Y_i}-\bar{Y})+(\overline{Y_i}-\bar{Y}{)}^2\right)-\sum _{i=1}^k\sum _{j=1}^{n_i}{\left(Y_{ij}-\overline{Y_i}\right)}^2\\ & =\sum _{i=1}^k\sum _{j=1}^{n_i}(Y_{ij}-\overline{Y_i}{)}^2-2\sum _{i=1}^k\sum _{j=1}^{n_i}\left((Y_{ij}-\overline{Y_i})(\overline{Y_i}-\bar{Y})\right)+\sum _{i=1}^k\sum _{j=1}^{n_i}(\overline{Y_i}-\bar{Y}{)}^2-\sum _{i=1}^k\sum _{j=1}^{n_i}{\left(Y_{ij}-\overline{Y_i}\right)}^2\\ & =\sum _{i=1}^k\sum _{j=1}^{n_i}(\overline{Y_i}-\bar{Y}{)}^2-2\sum _{i=1}^k\left((\overline{Y_i}-\bar{Y})\sum _{j=1}^{n_i}(Y_{ij}-\overline{Y_i})\right)(ps:\sum _{j=1}^{n_i}(Y_{ij}-\overline{Y_i})=0)\\ & =\sum _{i=1}^k{n}_i(\overline{Y_i}-\bar{Y}{)}^2(2.7)\end{array}$$
因为$\overline{Y_i}$可以视为对$a_i$的估计，$a_i$的差异越大，$\overline{Y_i}$之间的差异也越大，所以$S{S}_A$可以用来衡量不同水平之间的差异程度。

在统计学上，通常称$SS$为总平方和，$S{S}_A$为因素$A$的平方和，$S{S}_e$为误差平方和，分解式$SS=S{S}_A+S{S}_e$为该模型的方差分析。

基于上面的分析，我们可以得到假设（5.3）的一个检验方法：当比值$S{S}_A/S{S}_e$大于某一给定界限时，否定$H_0$，不然就接受$H_0$。为了构造$F$分布的检验统计量，我们假定随机误差$e_{ij}$满足正态分布$N(0,{\sigma }^2)$，同时我们也假定观察值$Y_{ij}$符合正态分布，此时，记
$$M{S}_A=S{S}_A/(k-1),M{S}_e=S{S}_e/(n-k)(2.8)$$
当$H_0$成立时，有：
$$M{S}_A/M{S}_e\sim F_{k-1,n-k}(2.9)$$
据（5.9），在给定显著性水平$\alpha$时，即得（5.3）的假设$H_0$的检验如下：
$$当M{S}_A/M{S}_e⩽F_{k-1,n-k}(\alpha )时，接受H_0，不然就拒绝H_0(2.10)$$
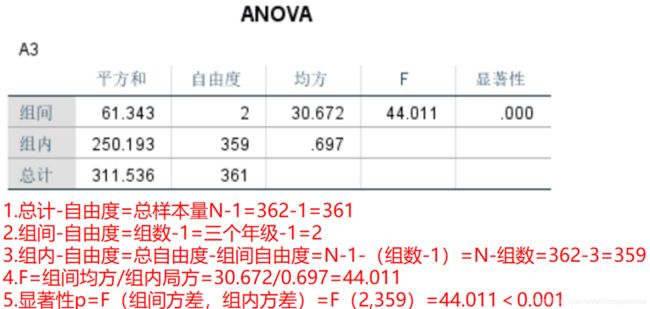
$M{S}_A$和$M{S}_e$分别被称为因素$A$和随机误差的平均平方和。被除数$k-1$和$n-k$，分别称为这两个平方和的自由度。$M{S}_e$的自由度为什么是$n-k$呢？因为平方和${\sum }_{j=1}^{n_i}{\left(Y_{ij}-\overline{Y_i}\right)}^2$的自由度为$n_i-1$，故对$i$求和，$S{S}_e$的自由度就是$n-k$。那么，$M{S}_A$的自由度为什么是$k-1$呢？因为一共有$k$个平均值$a_1,\cdots ,a_k$等$k-1$个，故自由度为$k-1$，两者自由度之和为$n-1$，恰好是总平方和的自由度。

到这里，我们可以做出方差分析表如表2-1

2-1 单因素方差分析的方差分析表

项目	$SS$	自由度	$MS$	$F$比	显著性
$A$	$S{S}_A$	$k-1$	$M{S}_A$	$M{S}_A/M{S}_e$	*, **, 或无
误差	$S{S}_e$	$n-k$	$M{S}_e$
总和	$SS$	$n-1$

在上表中，对于显著性一栏，一般来说，我们把算出的$F$比，即$M{S}_A/M{S}_e$，与$F_{k-1,n-k}(0.05)=c_1$和$F_{k-1,n-k}(0.01)=c_2$比较。若$M{S}_A/M{S}_e<c_2$，用**表示，表明A因素的效应是高度显著的，即在$\alpha =0.01$的显著性水平下，拒绝原假设（5.3）。同理，$c_2<M{S}_A/M{S}_e<c_1$用$\ast$表示，$M{S}_A/M{S}_e>c_1$时不显著。

2 代码实现

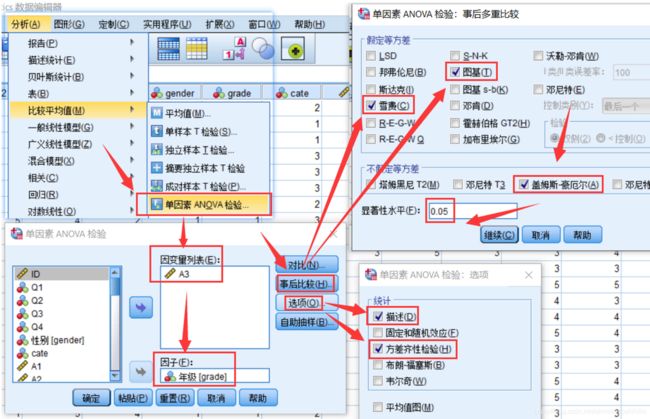
由于目前还没有接触过R，因此这部分的坑之后再来填，给出spss的实现过程和结果

三、双（多因素）因素方差分析

1 推导过程

在很多种情况下，只考虑一个指标对观察值的影响，显然是不够的，这时就会用到多因素方差分析。双因素方差分析和多因素方差分析在原理上是相似的，这里为了书写简便，我们只以双因素方差分析为例进行推导。

还是以田间实验的例子帮助理解推导过程，我们设有两个因素$A,B$，分别有$k,l$个水平（例如$A$为品种，有$k$个；$B$为播种量，考虑$l$种不同的数值，如20斤／亩，25斤／亩，……）．$A$的水平$i$与$B$的水平$j$的组合记为$(i,j)$，其试验结果记为 $Y_{ij},i=1,\cdot \cdot \cdot ,k,j=1,\dots ,l$．统计模型定为
$$Y_{ij}=\mu +a_i+b_j+e_{ij}，i=1,\cdot \cdot \cdot ,k,j=1,\cdot \cdot \cdot ,l(3.1)$$
为解释这模型，首先把右边分成两部分：$e_{ij}$为随机误差，它包含了未加控制的因素($A,B$以外的因素）及大量随机因素的影响．假定
$$E(e_{ij})=0,0<Var(e_{ij})={\sigma }^2<\infty ,一切e_{ij}独立同分布(3.2)$$
另一部分$\mu +a_i+b_j$，它显示水平组合$(i,j)$的平均效应．它可以又分解为三部分：$\mu$是总平均（一切水平组合效应的平均），是一个基准．$a_i$表示由$A$的水平$i$带来的增加部分，称为因素$A$的水平$i$的效应．$b_j$有类似的解释．调整$\mu$的值，我们可以补充要求：
$$a_1+\cdot \cdot \cdot +a_k=0,b_1+\cdot \cdot \cdot +b_l=0(3.3)$$
如果$(3.3)$式不成立，则分别把$\mu$换为 $\mu +\bar{a}+\bar{b}$，$a_i$换为$a_i-\bar{a}$，$b_j$换为$b_j-\bar{b}$，则$(3.1)$式不变，而$(3.3)$式成立。

约束条件$(3.3)$给了$a_i，b_j$的意义一种更清晰的解释：$a_i>0$ 表示A的水平$i$的效应在$A$的全部水平的平均效应之上，$a_i<0$ 则相反。另外，这个约束条件也给了$\mu ，a_i,b_j$的 一个适当的估计法：把$Y_{ij}$对一切$i,j$相加．注意到$(3.3)$，有
$$\sum _{i=1}^k\sum _{j=1}^l{Y}_{ij}=kl\mu +\sum _{i=1}^k\sum _{j=1}^l{e}_{ij}(3.4)$$
由$(3.2)$得，
$$\bar{Y}=\sum _{i=1}^k\sum _{j=1}^l{Y}_{ij}/kl(3.5)$$
是$\mu$的一个无偏估计。其次，有
$$\sum _{j=1}^l{Y}_{ij}=l\mu +la+\sum _{j=1}^l{e}_{ij}(3.6)$$
于是，记
$$\overline{Y_i}=\sum _{j=1}^l{Y}_{ij}/l,\overline{Y_j}=\sum _{i=1}^k{Y}_{ij}/k(3.7)$$
由$(3.7)$知，$\overline{Y_j}$为$\mu +a_i$的一个无偏估计。于是得到$a_i$的一个无偏估计为
$$\widehat{a_i}=\overline{Y_i}-\bar{Y},i=1,\cdots ,k(3.8)$$
同理，
$$\widehat{b_j}=\overline{Y_j}-\bar{Y},j=1,\cdots ,l(3.9)$$
$\widehat{a_i},\widehat{b_j}$适合约束条件$(3.3)$。

下面进行方差分析，要设法把总平方和
$$SS=\sum _{i=1}^k\sum _{j=1}^l(Y_{ij}-\bar{Y}{)}^2$$
分解为三部分：$S{S}_A,S{S}_B,S{S}_e$，分别表示因素$A,B$和随机误差的影响。这种分解的主要目的是假设检验：
$$H_{0A}:a_1=\cdots =a_k=0(3.10)$$
和
$$H_{0B}:b_1=\cdots =b_k=0(3.11)$$
$H_{0}A$成立表示因素$A$对指标其实无影响。在实际问题中，绝对无影响的场合少见，但如影响甚小以致被随机误差所掩盖时，这种影响事实上等于没有。因此，拿$S{S}_A$和$S{S}_e$的比作为检验统计量正符合这一想法．

接下来讲一下方差分解的小技巧：
$$Y_{ij}-\bar{Y}=(\overline{Y_i}-\bar{Y})+(\overline{Y_j}-\bar{Y})+(Y_{ij}-\overline{Y_i}-\overline{Y_j}+\bar{Y})$$
两边平方，对$i,j$求和，结合约束条件(3.3)，注意到
$$\sum _{i=1}^k(\overline{Y_i}-\bar{Y})=0，\sum _{j=1}^l(\overline{Y_j}-\bar{Y})=0，$$

$$\sum _{i=1}^k(Y_{ij}-\overline{Y_i}-\overline{Y_j}+\bar{Y})=\sum _{j=1}^l(Y_{ij}-\overline{Y_i}-\overline{Y_j}+\bar{Y})=0$$

即知所有交叉积之和皆为0，而得到
$$\begin{array}{rl}SS& =l\sum _{i=1}^k(\overline{Y_i}-\bar{Y}{)}^2+k\sum _{j=1}^l(\overline{Y_j}-\bar{Y}{)}^2+\sum _{i=1}^k\sum _{j=1}^l(Y_{ij}-\overline{Y_i}-\overline{Y_j}+\bar{Y}{)}^2\\ & =S{S}_A+S{S}_B+S{S}_e(3.12)\end{array}$$

第一个平方和可以作为因素$A$的影响的衡量，从前述$\overline{Y_i}-\bar{Y}$作为 $a_i$的估计可以理解第二个平方和同理。至于第三个平方和可作为随机误差的影响这一点， 直接看不甚明显。可以从两个角度去理解：在$SS$中去掉$S{S}_A$ 和$S{S}_B$后，剩余下的再没有其他系统性因素的影响，故只能作为$S{S}_e$。另外，由模型$(3.1)$及约束条件$(3.3)$，易知
$$\begin{array}{rl}{Y}_{ij}-\overline{Y_i}-\overline{Y_j}+\bar{Y}& =(\mu +a_i+b_j+e_{ij})-(\mu +a_i+\overline{e_i})-(\mu +b_j+\overline{e_j})+(\mu +\bar{e})\\ & =e_{ij}-\overline{e_i}-\overline{e_j}+\bar{e}(3.13)\end{array}$$
这里面已经毫无$\mu ,a_i,b_j$的影响，而只含随机误差。

得到分解式$(3.12)$后，我们就可以像单囚素情况那样，写出下面的方差分析表：
$S{S}_A,S{S}_B$ 自由度分别为其水平数减去1，这一点与单因素情况相同．总和自由度为全部观察值数目$kl$减去1．剩下的就是误差平方和自由度：
$$(kl-1)-(k-1)-(l-1)=(k-1)(l-1)$$
表3.1 双因素方差分析表

项目	$SS$	自由度	$MS$	$F$比	显著性
$A$	$S{S}_A$	$k-1$	$M{S}_A$	$M{S}_A/M{S}_e$	*, **, 或无
$B$	$S{S}_B$	$l-1$	$M{S}_B$	$M{S}_B/M{S}_e$
误差	$S{S}_e$	$(k-1)(l-1)$	$M{S}_e$
总和	$SS$	$kl-1$

还有一点要注意：在采纳模型$(3.1)$时，我们事实上引进了 一 种假定，即两因素$A,B$对指标的效应是可以叠加的．换一种方式说：因素$A$的各水平的优劣比较，与因素$B$处在哪个水平无关，反之亦然．更一般的情况是：$A,B$两因子有“交互作用 ＂ 。这时在模型(5.13)中，还要加上表示交互作用的项$c_{ij}$．这时不仅统计分析复杂化了，尤其是分析结果的解释也复杂化了．本文档暂不讨论这种情况。在一个特定的问题中，交互作用是否需要考虑，在很大程度上取决于问题的实际背景和经验．有时，通过试验数据的分析也可以看出一些问题。例如，若误差方差${\sigma }^2$的估计$M{S}_e$反常地大，则有可能是由于交互作用所致．因为可以证明：若交互作用确实存在而未加考虑，则它的影响进入随机误差而增大了$M{S}_e$。

2 代码实现

由于目前还没有接触过R，因此这部分的坑之后再来填，给出spss的实现过程和结果

---

最后

第一次参与了DW的组队学习，我觉得非常好，但是发现了自己理论和实践上都存在很大程度的不足，最近正好期末考试了，不能全身心投入学习和充电的工作，希望未来可以进一步完善自己该部分的内容，感谢组织！