《Python 深度学习》刷书笔记 Chapter 5 Part-4 卷积神经网络的可视化（Fillter）

---

可视化卷积神经网络

---

一直以来，人们都习惯将卷积神经网络的训练过程称为黑盒子，而我们现在就要解开这个盒子的秘密，进一步研究卷积神经网络在训练的过程中都做了些什么。

2-25 读入模组

---

from keras.models import load_model

model = load_model('cats_and_dogs_small_2.h5')

# 观察模型基本概况
model.summary()

Model: "sequential_2"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
conv2d_5 (Conv2D)            (None, 148, 148, 32)      896       
_________________________________________________________________
max_pooling2d_5 (MaxPooling2 (None, 74, 74, 32)        0         
_________________________________________________________________
conv2d_6 (Conv2D)            (None, 72, 72, 64)        18496     
_________________________________________________________________
max_pooling2d_6 (MaxPooling2 (None, 36, 36, 64)        0         
_________________________________________________________________
conv2d_7 (Conv2D)            (None, 34, 34, 128)       73856     
_________________________________________________________________
max_pooling2d_7 (MaxPooling2 (None, 17, 17, 128)       0         
_________________________________________________________________
conv2d_8 (Conv2D)            (None, 15, 15, 128)       147584    
_________________________________________________________________
max_pooling2d_8 (MaxPooling2 (None, 7, 7, 128)         0         
_________________________________________________________________
flatten_2 (Flatten)          (None, 6272)              0         
_________________________________________________________________
dropout_2 (Dropout)          (None, 6272)              0         
_________________________________________________________________
dense_3 (Dense)              (None, 512)               3211776   
_________________________________________________________________
dense_4 (Dense)              (None, 1)                 513       
=================================================================
Total params: 3,453,121
Trainable params: 3,453,121
Non-trainable params: 0
_________________________________________________________________

5-26 观察图像

---

# 读入图像

img_path = r'E:\code\PythonDeep\DataSet\dogs-vs-cats\train\cat.1700.jpg'

# 将图像处理为一个4D的tenser张量
from keras.preprocessing import image
import numpy as np

img = image.load_img(img_path, target_size = (150, 150))
img_tensor = image.img_to_array(img)

# 按行扩充
img_tensor = np.expand_dims(img_tensor, axis = 0)

# 记住我们要对输入变量进行归一化处理
img_tensor /= 255

# 打印图像张量
print(img_tensor.shape)

(1, 150, 150, 3)

# 打印图像
import matplotlib.pyplot as plt

# 注意这是一个4D张量
plt.imshow(img_tensor[0])
plt.show()

观察卷积层特征提取

---

为了能够进一步抽取图像，我们创建了一个Keras的模型，然后将图片输入进去，在输入的过程中，我们在观察特定的卷积层的输出

5-27 建立多输出模型观察输出

---

from keras import models

# 提取最顶层前8层的输出
# 注意，这里是“前”8层，也就是说这些输出的层是叠加态的
layer_outputs = [layer.output for layer in model.layers[:8]]

# 将数据喂给模型
activation_model = models.Model(inputs = model.input, outputs = layer_outputs)

# 返回一个5个元素的Numpy的一元数组
activations = activation_model.predict(img_tensor)

# 打印输出图像的信息
first_layer_activation = activations[0]
print(first_layer_activation.shape)

(1, 148, 148, 32)

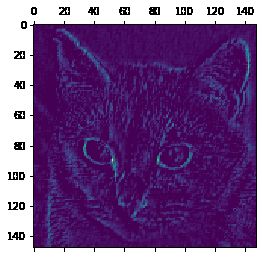
5-28 显示图像

---

import matplotlib.pyplot as plt

# 显示在第三层的图像
plt.matshow(first_layer_activation[0, :, :, 3], cmap = 'viridis')
plt.show()

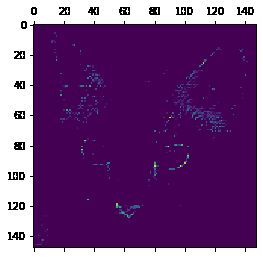
我们继续深入，观察第29层的图像

plt.matshow(first_layer_activation[0, :, :, 29], cmap='viridis')
plt.show()

可以看到，随着层次的加深，卷积网络所识别的部位更加具体了

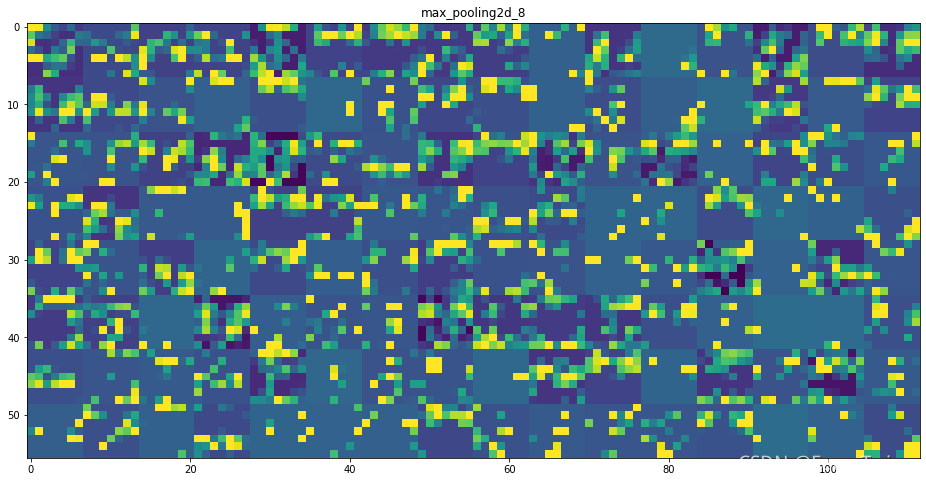
5-29 打印全部的识别图

---

import keras

# 存储层数
layer_names = []
for layer in model.layers[:8]:
    layer_names.append(layer.name)

images_per_row = 16

# 显示图像集合
for layer_name, layer_activation in zip(layer_names, activations):
    # 在图像集合里的数字
    n_features = layer_activation.shape[-1]
    
    # 图像的张量形状 (1, size, size, n_features)
    size = layer_activation.shape[1]
    
    # 对矩阵中的每一个设置激活通道
    n_cols = n_features // images_per_row
    display_grid = np.zeros((size * n_cols, images_per_row * size))
    
    # 从水平方向上填充图形
    for col in range(n_cols):
        for row in range(images_per_row):
            channel_image = layer_activation[0,
                                             :, :,
                                             col * images_per_row + row]
            
            # 标准化
            channel_image -= channel_image.mean()
            channel_image /= channel_image.std()
            channel_image *= 64
            channel_image += 128
            channel_image = np.clip(channel_image, 0, 255).astype('uint8')
            display_grid[col * size : (col + 1) * size,
                         row * size : (row + 1) * size] = channel_image
    
    # 显示整个网格
    scale = 1. / size
    plt.figure(figsize = (scale * display_grid.shape[1],
                          scale * display_grid.shape[0]))
    plt.title(layer_name)
    plt.grid(False)
    plt.imshow(display_grid, aspect = 'auto', cmap = 'viridis')
    
plt.show()

5-32 为过滤器的可视化定义损失张量

---

from keras.applications import VGG16
from keras import backend as K

model = VGG16(weights = 'imagenet', 
              include_top = False)

layer_name = 'block3_conv1'
filter_index = 0

layer_output = model.get_layer(layer_name).output
loss = K.mean(layer_output[:, :, :, filter_index])

5-33 获取损失相对于输入的梯度

---

grads = K.gradients(loss, model.input)[0] # 返回一个张量列表，只保留第一个元素

5-34 梯度标准化

---

grads /= (K.sqrt(K.mean(K.square(grads))) + 1e-5)

5-35 给定输入numpy值，得到numpy输出

---

iterate = K.function([model.input], [loss, grads])

import numpy as np
loss_value, grads_value = iterate([np.zeros((1, 150, 150, 3))])

5-36 通过随机梯度下降将让损失最大化

---

input_img_data = np.random.random((1, 150, 150, 3)) * 20 + 128.

# 每次梯度更新的步长
step = 1.

for i in range(40):
    loss_value, grad_value = iterate([input_img_data])
    
    input_img_data += grads_value * step

5-37 张量转换为有效图像的实用函数

---

def deprocess_image(x):
    # 对张量作标准化
    x -= x.mean()
    x /= (x.std() + 1e-5)
    x *= 0.1
    
    # 将x裁切到区间[0, 1]之间
    x += 0.5
    x = np.clip(x, 0, 1)
    
    # 将x转换为RGB数组
    x *= 255
    x = np.clip(x, 0, 255).astype('uint8') # 对数据类型进行转换    
    return x

5-38 生成过滤器可视化的函数

---

import matplotlib.pyplot as plt
# 一个可以将过滤器转换为图像并进行可视化的函数
def generate_pattern(layer_name, fliter_index, size = 150):
    # 构建一个损失函数，将第n个过滤器最大化
    layer_output = model.get_layer(layer_name).output
    loss = K.mean(layer_output[:, :, :, filter_index])
    
    # 计算这个损失相对于输入图像的梯度
    grads = K.gradients(loss, model.input)[0]
    
    # 梯度标准化
    grads /= (K.sqrt(K.mean(K.square(grads))) + 1e-5)
    
    # 返回输入图像的损失和精度
    iterate = K.function([model.input], [loss, grads])
    
    # 带噪声的灰度图像
    input_img_data = np.random.random((1, size, size, 3)) * 20 +128.
    
    # 进行40次梯度上升
    step = 1.
    for i in range(40):
        loss_value, grads_value = iterate([input_img_data])
        input_img_data += grads_value * step
        
    img = input_img_data[0]
    return deprocess_image(img)

---

从上图可知，block3_conv1层的0个过滤器是波尔卡点，我们接下来将查看每一层的前64个过滤器，我们将输出放在一个88的网格种，每个网格是64像素64像素

---

5-39 生成某一层中所有过滤器响应模式组成的网络

---

for layer_name in ['block1_conv1', 'block2_conv1', 'block3_conv1', 'block4_conv1']:
    size = 64
    margin = 5

    # 生成一个空图像，用于保存结果
    results = np.zeros((8 * size + 7 * margin, 8 * size + 7 * margin, 3))

    # 遍历results网格的行
    for i in range(8):
        # 遍历results网格的列
        for j in range(8):
            # 生成layer_name层第 i + 8 个过滤器的模式
            filter_img = generate_pattern(layer_name, i + (j * 8), size = size)

            # 将结果放到results网格的第（i，j）个方块中
            horizontal_start = i * size + i * margin
            horizontal_end = horizontal_start + size
            vectical_start = j * size + j * margin
            vectical_end = vectical_start + size

            # 添加结果
            results[horizontal_start : horizontal_end,
                    vectical_start : vectical_end, :] = filter_img

    # 显示result网格
    plt.figure(figsize = (20, 20))
    # plt.imshow(results) # 这句话需要改，输出为0-1之间的值
    plt.imshow(results.astype('uint8'))
    
# for layer_name in ['block1_conv1', 'block2_conv1', 'block3_conv1', 'block4_conv1']:
#     size = 64
#     margin = 5

#     # This a empty (black) image where we will store our results.
#     results = np.zeros((8 * size + 7 * margin, 8 * size + 7 * margin, 3))

#     for i in range(8):  # iterate over the rows of our results grid
#         for j in range(8):  # iterate over the columns of our results grid
#             # Generate the pattern for filter `i + (j * 8)` in `layer_name`
#             filter_img = generate_pattern(layer_name, i + (j * 8), size=size)

#             # Put the result in the square `(i, j)` of the results grid
#             horizontal_start = i * size + i * margin
#             horizontal_end = horizontal_start + size
#             vertical_start = j * size + j * margin
#             vertical_end = vertical_start + size
#             results[horizontal_start: horizontal_end, vertical_start: vertical_end, :] = filter_img

#     # Display the results grid
#     plt.figure(figsize=(20, 20))
    
#     plt.imshow(results.astype('uint8'))
# #     plt.imshow(results)
#     plt.show()

总结

---

• 这些过滤器可视化包含卷积神经网课层如何观察世界，卷积神经网络的每一层都学习了一组过滤器，然后将输入表示为过滤器的组合
• 随着输入的加深，卷积神经网络的过滤器也变得越来越复杂，越来越精细
• 模型的第一层：简单的方向边缘以及颜色
• 第二层：颜色组合以及简单纹理
• 更高层的过滤器有更高的特征，如羽毛、眼睛、树叶等

---

写在最后

注：本文代码来自《Python 深度学习》，做成电子笔记的方式上传，仅供学习参考，作者均已运行成功，如有遗漏请练习本文作者

各位看官，都看到这里了，麻烦动动手指头给博主来个点赞8，您的支持作者最大的创作动力哟！
＜（＾－＾）＞
才疏学浅，若有纰漏，恳请斧正
本文章仅用于各位同志作为学习交流之用，不作任何商业用途，若涉及版权问题请速与作者联系，望悉知