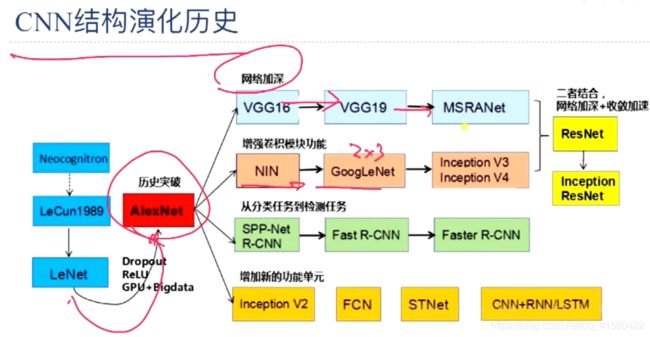
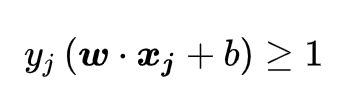神经网络与深度学习理论,tensorflow2.0教程,cnn

*免责声明:
1\此方法仅提供参考
2\搬了其他博主的操作方法,以贴上路径.
3*

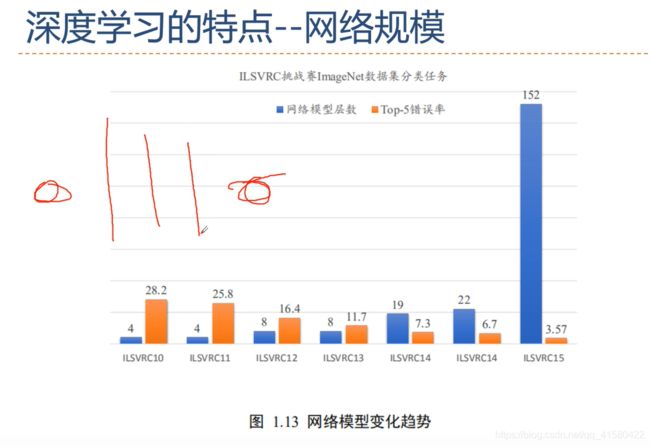
场景一:神经网络与深度学习理论

场景二:tensorflow的安装

场景三:numpy包介绍

场景四:机器学习基础

场景五:线性回归模型

场景六:神经网络

场景七:TensorFlow2.0

场景八:tf.Keras相关操作

场景九:卷积神经网络

课程学习地点

神经网络与深度学习 --邱锡鹏 —全书pdf

…

场景一:神经网络与深度学习理论

1.1 相互关系

1.2 发展特点

1.3 应用



1.4 框架介绍

场景二:tensorflow的安装

1.1 windows+cpu安装tensorflow

参考博客

Cpu版本的tensorflow2.0的简易安装
在anaconda中 输入conda create -n tf2 python=3.8.5
这句话是在anaconda中创建了一个名叫tf2的环境,用的python版本是3.8.5
命令:activate tf2 #进入tf2的环境，激活

conda install tensorflow #安装tensorflow的包 安装好进入python下

import tensorflow as tf
print(tf.__version__)

结果 2.3.0

说明:这里导入成功包,不过是在anconda下里虚拟了一个环境名字叫tf2。
当然我们使用tensorflow的包可以每次进入这个环境，然后命令行编码，显然这不太方便。 当我们使用jupyter nootbook的时候，这个默认的是anaconda的base环境，base环境中可没有我们指定的tensorflow的包。这时候创建文件导入tensorflow的包会报错。

解决方法一：在base下安装tensorflow的包，conda install tensorflow

#解决方法二：将tf2的环境加入到jupyter  nootbook的启动项中。
# 第一步，切换到想要添加的虚拟环境：
conda activate tf2
# 第二步，安装ipykernel包
conda install ipykernel
# 第三步，执行如下命令，并确定环境的名称（此处设置为data）
python -m ipykernel install --name tf2

重新启动  jupyter  nootbook

补充命令：查看所有已创建的anaconda环境 conda env list
查看目前notebook文件在哪个环境下运行

import os, sys
print(sys.executable) # works this time
print(sys.version)
print(sys.version_info)

Windows退出环境：activate root
检查更新当前conda conda update conda
删除tf2的环境 conda remove -n tf2 --all

1.2 linux (ubuntu) 下安装

pip  install  tensorflow=2.0.0

测试

import  tensorflow as tf

tf.__version__

#查看gpu是否可用
tf.test.is_gpu_available()

…

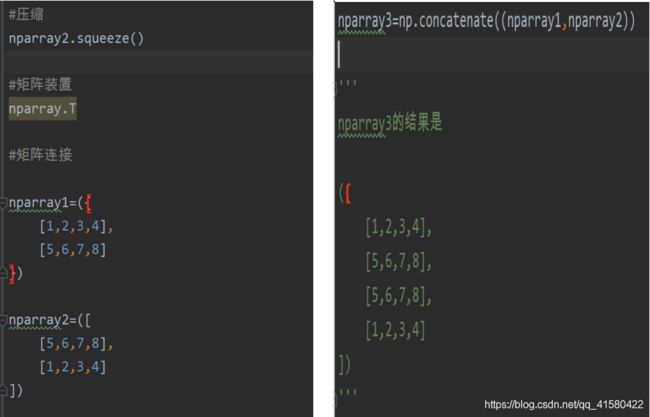
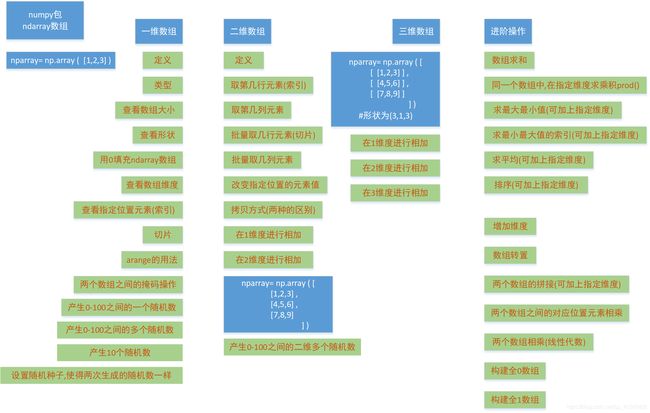
场景三:numpy包介绍

ndarray数组
.

1.1 一维数组

#科学计算库
import numpy as  np
'''
#对于一维数组
'''
#numpy的数组的不同
array=[1,2,3] #这是一个list类型,不能进行array+1

#但是如果是一个numpy的数组是可以的 
nparray=np.array([1,2,3])  #类型是ndarray的类型
nparray+1  #结果为arry([2,3,4])

nparray.dtype  #这个相当于查看数组里面的数据类型
nparray.size  #大小
nparray.shape  #形状

nparray.ndim #维度
nparray.fill(0)  #表示用0填充

nparray[0] #索引
nparray[0:2]  #切片


nparray=np.arange(开始,结束,步长)

nparray=([0,10,20,30,40,50])
nparray2=np.array([0,1,0,6,0,4],dtype=bool)
#nparray2对应的取值为([false,true, false,true, false,true ]) 相当于正数为true

nparry[nparray2] 
#  将nparray2作为索引传给nparray,这个时候  
# 对应的值([10,30,50]),相当于把true对应的索引值留了下来

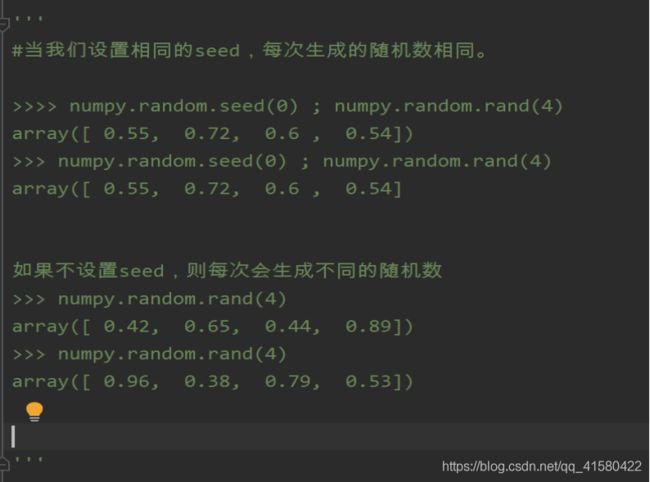
nparray=np.random.rand(10)  #随机产生10个随机数
nparray=np.random.randint(0,100)  #随机产生0-100的1个随机数

nparray=np.random.randint(0,100,size=3)  #随机产生0-100的3个随机数
nparray=np.random.randint(0,100,size=(3,3))  #随机产生0-100的3x3矩阵的二维9个随机数

'''随机二维的结果
               array ([[80, 55, 69],
                       [13, 20, 78],
                       [27, 98, 49]])
...

1.2 二维数组

'''
＃二维数组
'''
nparray=np.array([  [1,2,3],[4,5,6],[7,8,9]  ])
nparray.shape  # (3,3)


nparray[1]  #输出的结果是([4,5,6])
nparray[:,1]  #输出的结果是([2,5,8]),冒号的用法相当于取第几列,
nparray[:,1:３]  #输出的结果是(［[2,3],[5,6],[8,9]］),冒号的用法相当于取第２,３列
nparray[1,1]=100  #相当于1维1列的制定地方赋值,([1,2,3],[4,100,6],[7,8,9])

nparray2=nparray  #这种赋值方式 nparray2的变化影响nparray
nparray2=nparray.copy()   #不影响  


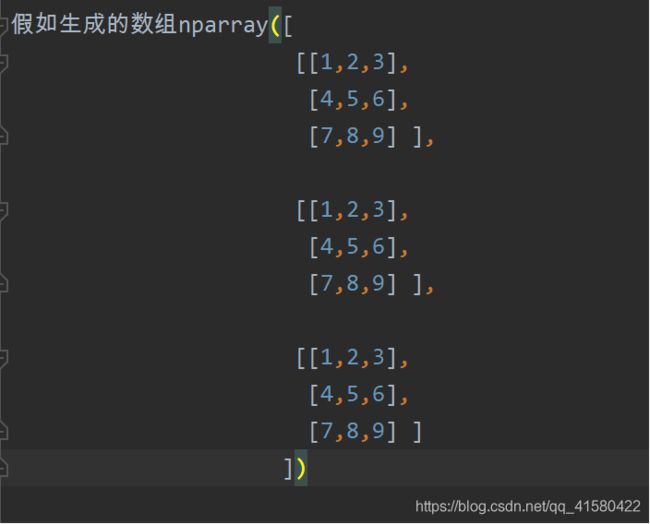
＃假如生成的数组nparray(［ [1,2,3]
                     　　 [4,5,6]
                   　 　  [7,8,9]］ )
np.sum(nparray)    ＃生成的ndarray类型的数组求和，及１＋．．．．＋９
np.sum(nparray,axis=0)   #axis=0代表０维　相当于把列和作为元素,([12,15,18])
np.sum(nparray,axis=1)   #axis=1代表１维　相当于把行和作为元素,([6,15,24])

1.3 三维数组

1.4 进阶操作

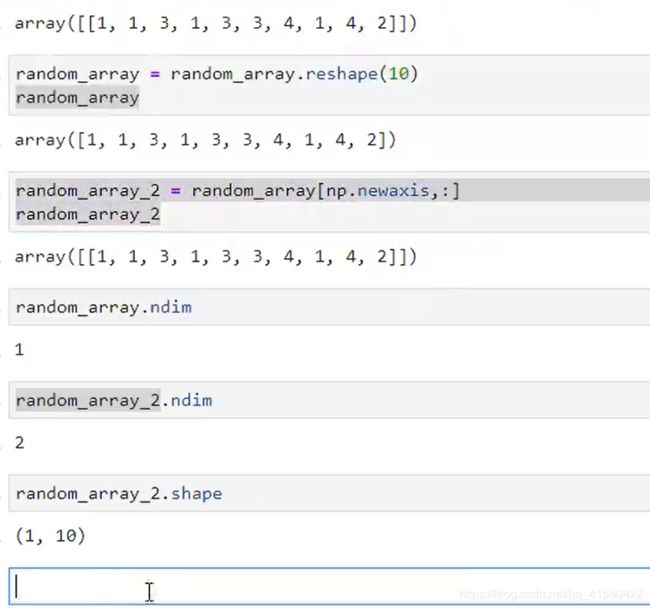
增加维度或重塑形

np.random.shuffle( 数组/数据集)     #随机打乱

np.random.normal(1,2,2) #生成两个符合均值为1，标准差为2高斯分布的概率密度随机数
np.random.normal(0,1,2) #生成两个符合均值为0，标准差为1标准正态分布的概率密度随机数
np.random.normal(loc, scale, size)返回一组符合高斯分布的概率密度随机数。

…

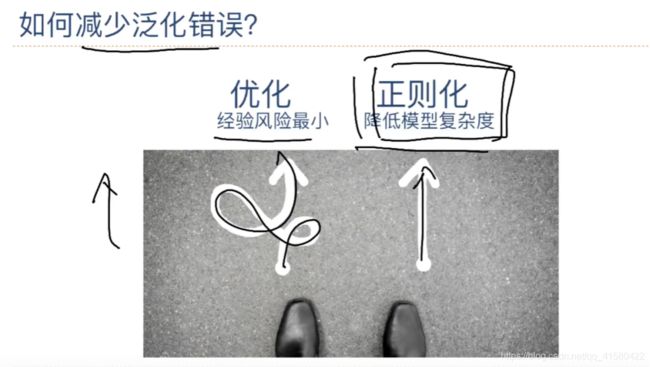
场景四:机器学习基础

文科生都能看懂的机器学习科普

1.1 基本概念

1.2 机器学习三要素

1.2.1 学习准则

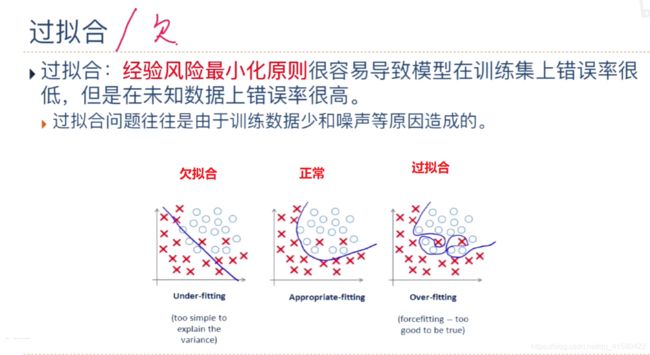
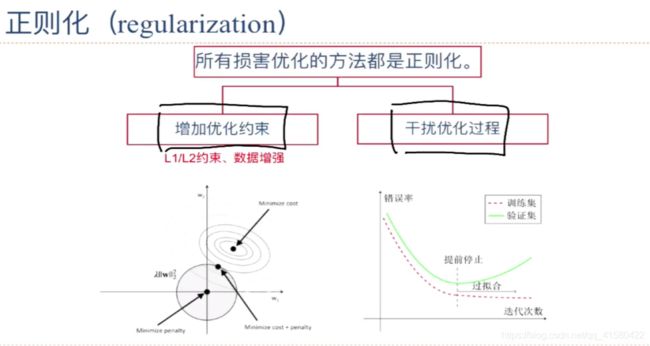
为了解决过拟合问题,一般在风险最小化的基础上再引入参数的正则化来限制模型的泛化能力. 使其不要过度的最小化经验风险

1.2.2 优化

梯度下降

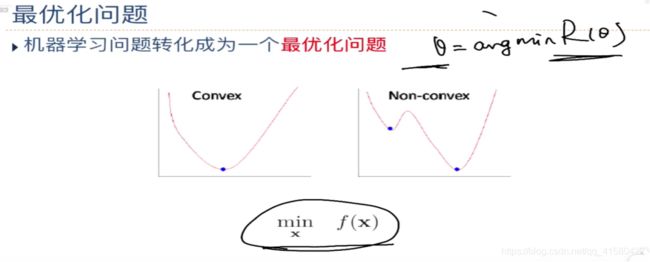
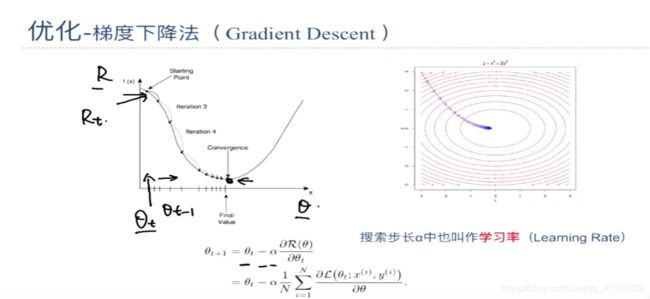
期望找到一个最小值,求导为0;

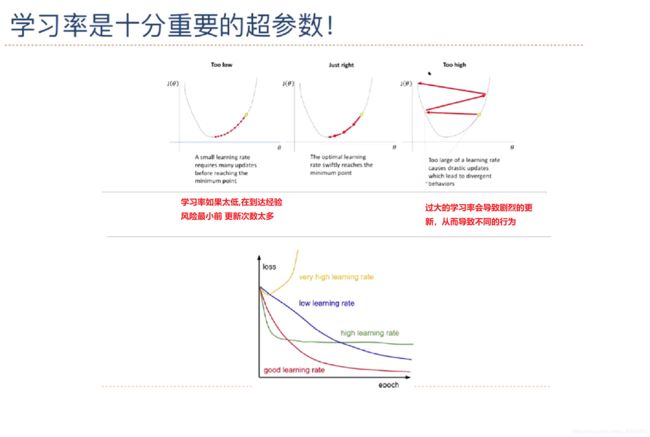
模型进行调参与优化,调的是 学习率 ɑ 和参数θ

#随机梯度下降法在一元方程上实战
import numpy  as np
import matplotlib.pyplot as plt   #画图的库
'''
1、构建数据集
目标y=2*x
'''
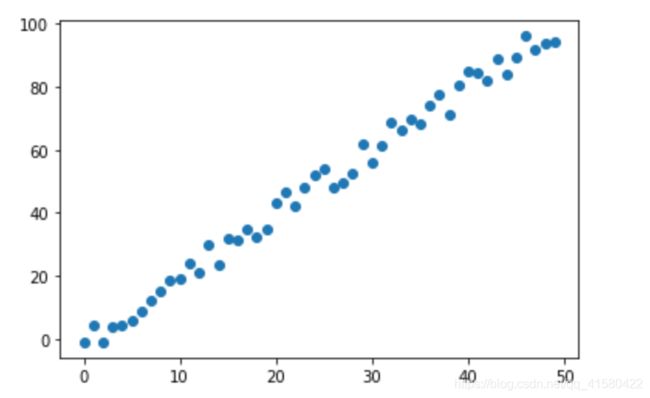
x=np.arange(0,50)

#[-5,5]
np.random.seed(1)
RandomArray=(np.random.rand(50)*2-1)*5
#np.random.random(50)  随机产生50个0-1的噪声值,  *2是[0-2] 减1以后是[-1,1]

y=2*x+RandomArray
plt.scatter(x,y)
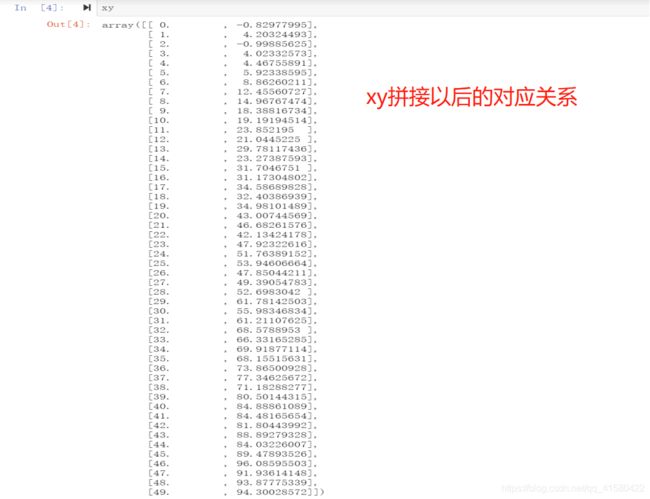
#将x与y拼接到一起,构建xy数据集
x=x.reshape(50,1)
y=y.reshape(50,1)
xy=np.concatenate((x,y),axis=1)

由上面可知,xy是有序的，在划分数据集的时候，我们应该随机的取其中的值作为训练和测试样本。在这里我们采用先打乱xy数据集，然后取前40个样本作为训练样本。

#划分样本为训练集和测试集 如按4:1划分
#打乱xy
np.random.shuffle(xy)

train_data=xy[0:40]
test_data=xy[40:]

#实现随机梯度下降算法SGD
lr=0.01    #自定义学习率
N=100      #N是超参数
epsilon=200    #确定错误率不再下降  值可以参考np.sum( xy[:,0]*2- xy[:,1]  )    相当于求真实值与预测值 所有误差的和
theta=np.random.rand()      #随机参数化theta

Num=1
theta_list=[]
loss_list=[]

while True:
    #重新排序训练集
    np.random.shuffle(train_data)

    for  n in range(N):
        randint = np.random.randint(0,40)   #随机数
        rand_x = train_data[randint][0]
        rand_y = train_data[randint][1]

        #计算梯度
        grad= rand_x  * (rand_x * theta - rand_y)
        #更新theta
        theta = theta - lr *grad
    #计算更新theta以后的错误率
    x=train_data[:,0]
    y=train_data[:,1]
    loss  =  np.sum(0.5* (theta*x -y )**2)       #平方差损失函数

    print("Number: %d, theta: %f , loss: %f"%(Num,theta,loss))
    Num = Num + 1
    theta_list.append(theta)
    loss_list.append(loss)

    if loss< epsilon:
        break
plt.plot( range( len(theta_list) ), theta_list )
plt.plot( range( len(loss) ), loss)

#挑战 编写目标函数 y= 3x+6的 SGB的实践
.
参考一: 彻底理解一元线性回归——梯度下降法
参考二: 实战梯度下降法实现一元线性回归

   对于y= ax  +b  方程 ,   a 就是上面的theta  
   
   随机梯度下降中,对于一元线性方程
   a的梯度 :     x  * (  a * x + b  - y )
   更新 a  :     a= a -  lr *  a的梯度

   b的梯度 :     a * x  + b  - y
   更新 b  :      b= b -  lr *  b的梯度
 

#目标  SGD 实现 y = 3 * x + 6 的线性回归

import  numpy as np 
import  matplotlib.pyplot as plt

#第一步 : 构建数据集 

x  = np.arange(50)   #构建x

N1 = (np.random.rand(50) * 2 -1) * 5   #构建50个噪音偏执
y  = 3 * x + 6 + N1  #构建y

#配对x,y
x = x.reshape(50 ,1)
y = y.reshape(50 ,1)
xy = np.concatenate( (x,y) , axis = 1 )


#第二步 : 构建训练集和测试集
np.random.shuffle( xy ) #打乱数据集
train_db = xy[0:40]
test_db=xy[40:]


#第三步: 进行求解theta


lr = 0.01 #学习率

N = 100

tloss = 200 #目标损失临界点

theta = np.random.rand( ) #随机初始化theta
b = np.random.rand( ) #随机初始化b


Num=1
theta_list=[]
loss_list=[]


while True:
    
    np.random.shuffle(train_db)#重新排序训练集
    
    for n in  range(N):
        i = np.random.randint( 0 ,40 )  #随机生成一个0-40的索引
        xi  = train_db[i][0]   #获取第a个的x部分
        yi = train_db[i][1]  #获取y部分
        
        #计算  对于y= ax  +b   a 就是上面的theta 
        
        b_gr =  xi * theta + b - yi  #计算b的梯度
        b = b - lr * b_gr      #更新theta梯度
        
        theta_gr =  xi *  ( xi * theta + b - yi )  #计算theta的梯度
        theta = theta - lr * theta_gr      #更新theta梯度
         
    #计算更新theta以后的错误率
    x1=train_db[:,0]
    y1=train_db[:,1]
    loss  =  np.sum(0.5* (theta*x1 -y1 )**2)       #平方差损失函数

    print("Number: %d, theta: %f , loss: %f"%(Num,theta,loss))
    
    Num = Num + 1
    theta_list.append(theta)
    loss_list.append(loss)

    if loss< tloss:
        break
plt.plot( range( len(theta_list) ), theta_list )
plt.plot( range( len(loss) ), loss)

1.3 示例_线性回归-探究参数学习方法

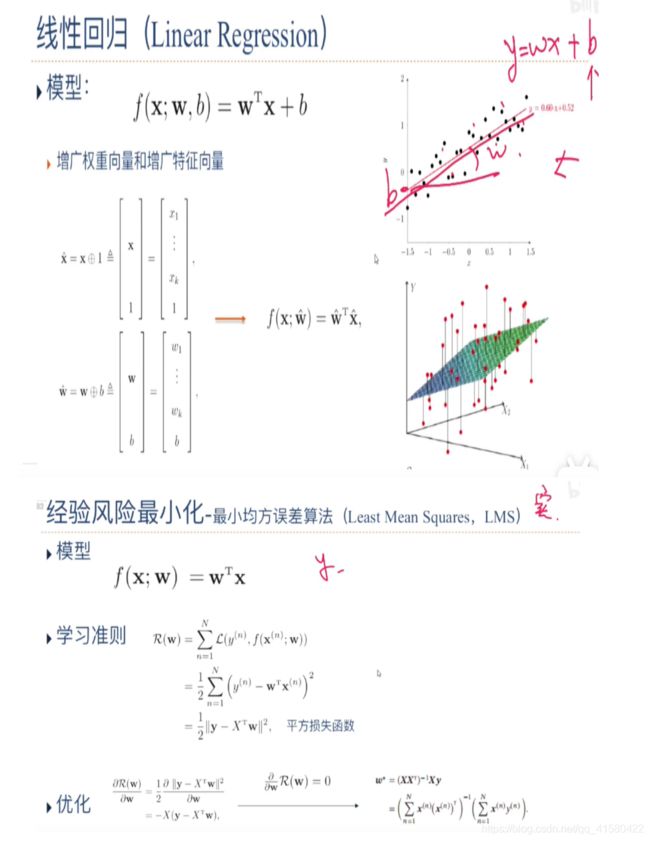
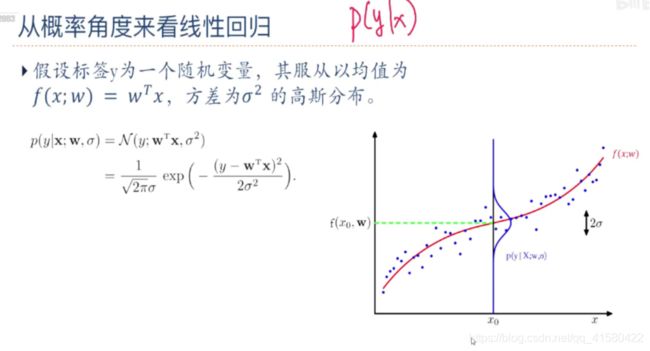
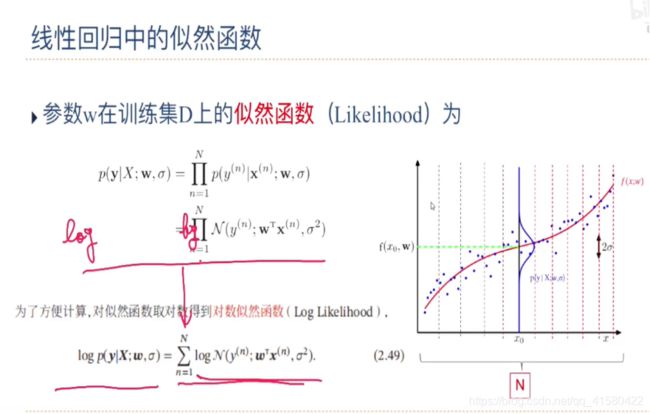
给定一组包含 个训练样本的训练集 = {((), ())} =1，我们希望能够学习一个最优的线性回归的模型参数．

我们介绍四种不同的参数估计方法：经验风险最小化、结构风险最小化、最 大似然估计、最大后验估计．

经验风险最小化(最小二乘法)

结构风险最小化(岭回归)

最大似然估计

机器学习任务可以分为两类：
.
1: 一类是样本的特征向量 和标签 之间存 在未知的函数关系 = ℎ()，
2: 另一类是条件概率(|) 服从某个未知分布．

#最小二乘法求一元线性回归
import numpy  as np
import matplotlib.pyplot as plt   #画图的库
'''
1、构建数据集
目标y=4*x + 2
'''
np.random.seed(0)
x=np.random.normal(size=(100,1),scale=1)   #随机产生

y=4*x[:,0]+2
plt.scatter(x,y)

xy=np.concatenate((x,y.reshape(100,1)),axis=1)
#将xy拼接在一起,构成数据集

#划分样本为训练集和测试集 如按7:3划分
#打乱xy
np.random.shuffle(xy)
train_data=xy[0:70,:]
test_data=xy[70:,:]

#构建模型
#随机初始化参数
w=np.random.normal(size=(1))
b=np.random.rand()

##定义损失函数

lr=0.001  #学习率

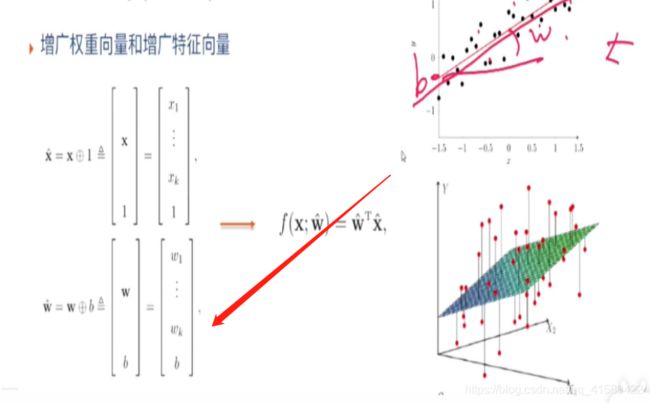
#构造增广矩阵

w_hat=np.concatenate(  (w,np.array([b])) )   #构造增广权重向量
w_hat=w_hat.reshape(2,1)

x=train_data[:,-1]
x=x.reshape(1,70)
x_hat=np.concatenate(  (x,np.ones(1,1) ) )   #构造增广特征向量

Num=1
while True
    #更新参数
    w_hat=w_hat + lr *np.dot(x_hat,( y.reshape(70,1)-np.dot(x_hat.T,w_hat)) )
    #相当于在上面提到过的 theta =  theta - lr * theta _ gr  (  其中theta_gr =  x   *   (theta*x - y ))

    #计算经验错误
    loss= np.sum( (y.reshape(70,1)-np.dot(x_hat.T,w_hat))**2  )/2
    #这里就相当于上面的 loss =  np.sum( 0.5*    (theta * x -y) **2   )

    #记录w,b 和loss
    w_list.append(w_hat[0])
    b_list.append(w_hat[1])
    loss_list.append(loss)
    Num=Num+1
    print("Number: %d, loss: %f"(Num,loss))

    if loss<1  or Num  >1000:
        break

    plt.plot(loss_list)  #损失图像
    plt.plot(w_list)  #最后就是4,
    plt.plot(b_list)  #无限收敛于2
#其实这里和上面1.3中的随机梯度下降的实践没有本质的区别,无非就是把wb变为了增广矩阵,而把上面的x变为增广向量,不过要注意数据的形状

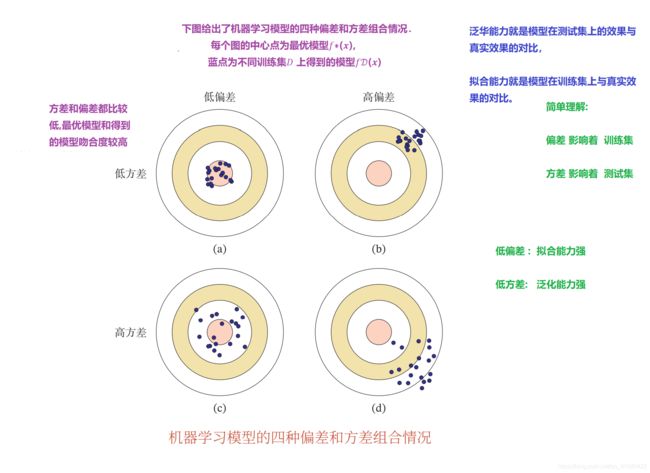
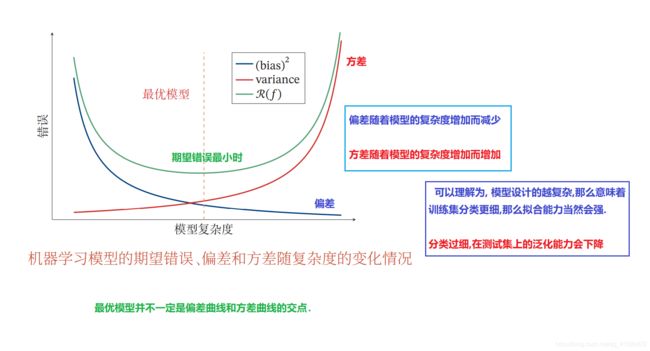
1.4 模型选择—偏差和方差分解

最优:意味着偏差低(在测试集上 拟合能力最好 ) 方差也低(在测试集上的泛化能力最好)

1.5 其他知识

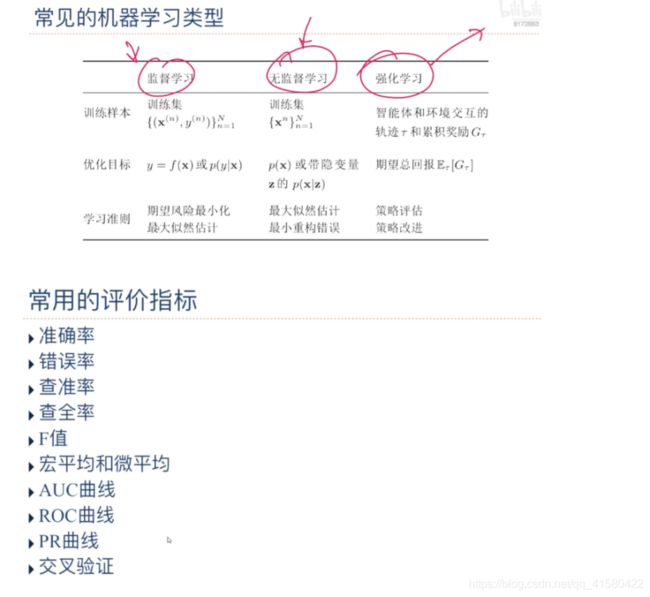
机器学习算法的类型/数据的特征表示/评价指标

监督学习需要每个样本都有标签，而无监督学习则不需要标签．

…

场景五:线性回归模型

良好的判断力来源于经验，而经验则往往来自于错误的判断。
.

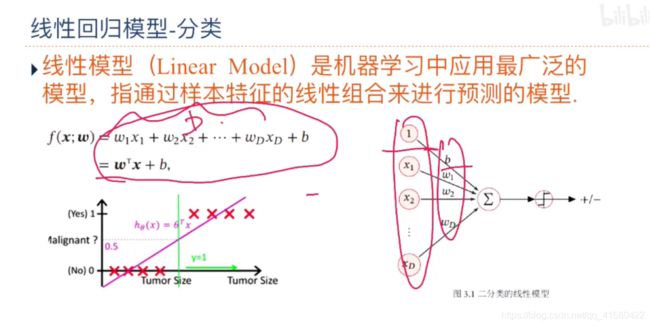
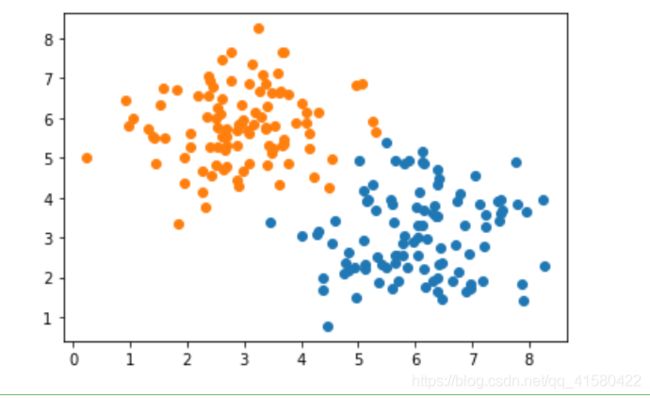
1.1 分类问题

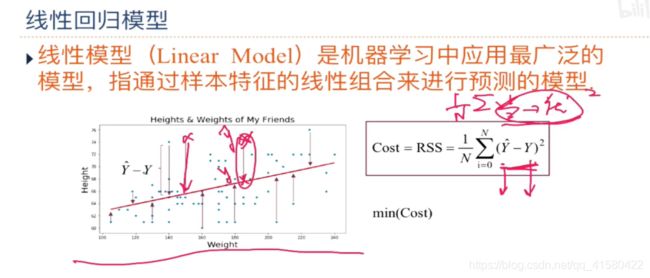
上一章中介绍的线性回归就是典型的线性模型，直接用(; )来预测输出目标 = (; )．

多分类

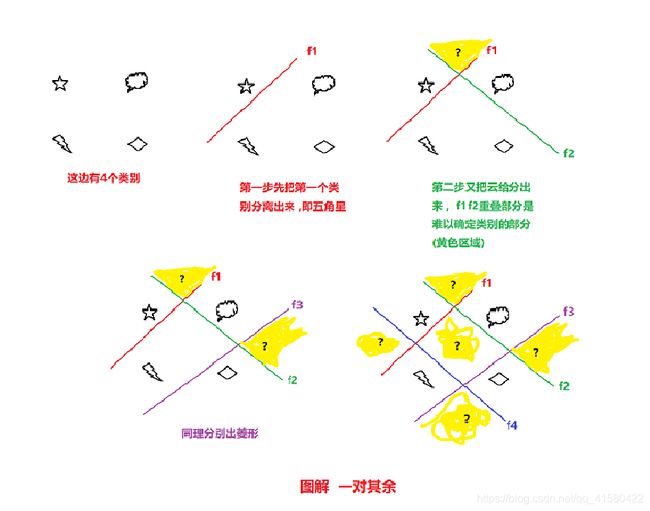
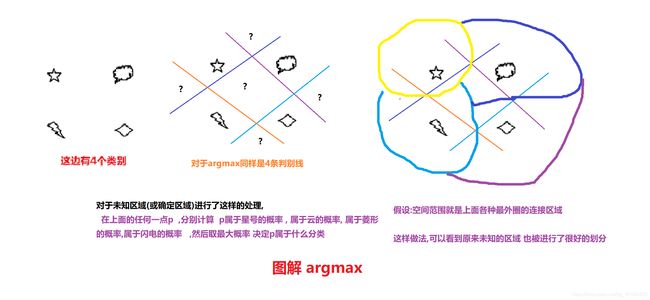
“一对其余”方式和“一对一”方式都存在一个缺陷：特征空间中会存在一 些难以确定类别的区域，而“argmax”方式很好地解决了这个问题．

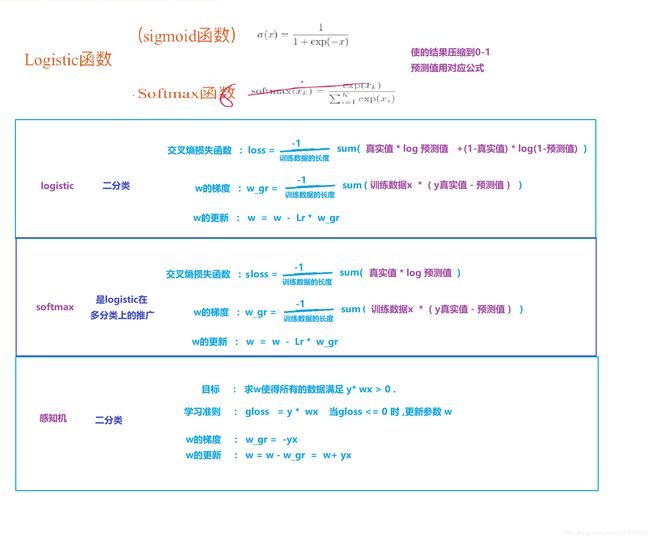
我们主要介绍四种不同线性分类模型：Logistic回归、Softmax回归、
感知器和支持向量机，这些模型的区别主要在于使用了不同的损失函数．

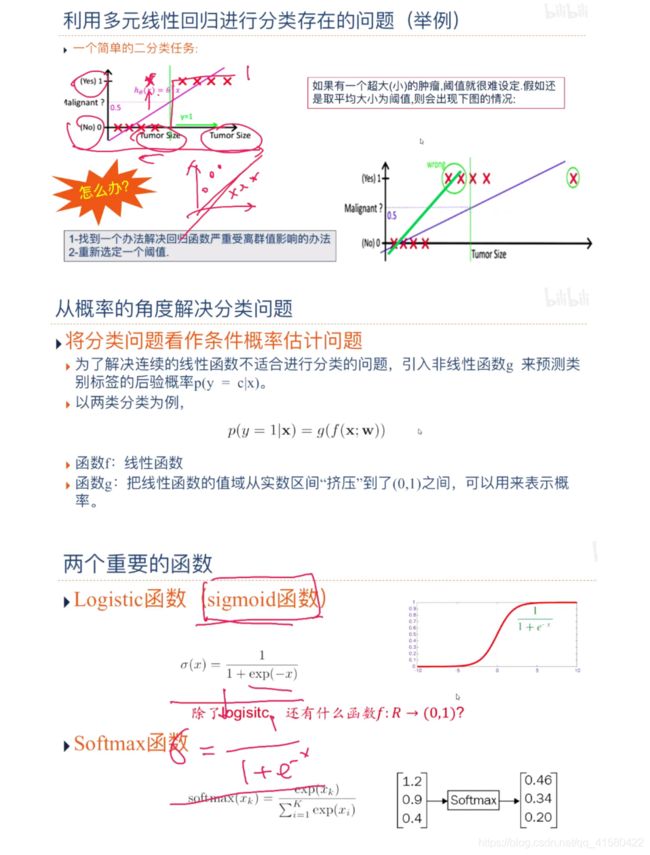
1.2 logistic回归-- 对数几率回归

Logistic 回归采用交叉熵作为损失函数，并使用梯度下降法来对参数进行 优化．

自信息就是信息量 -log( p(x) )

例如 现在有一场足球决赛 中国对阵德国 ,谁赢得冠军的几率大?

就目前2021年而言, 当然是德国的概率更大一些.

比如:现在有一则新闻播报结果, 德国获得世界冠军,这个包含的信息量比较小
因为人们大概率已经认定了德国会赢.
现在有一则新闻播报结果, 中国对获得世界冠军,这个包含的信息量比较大.

这就是上面的概率越小,信息量越大 .    信息量: -log( p(x)  )

p(x) = 1 ,就是肯定会发生  ,那么包含的信息量为0

熵 : 就是所有信息量的期望 -p(x) log( p(x) )

有这样的概率  0.7 , 0.3 , 0.1   
那么熵为:  - ( 0.7 * log 0.7 + 0.3 * log 0.3 + 0.1 * l og 0.1 )

二分类 : p 和 l-p
熵 H(x) =  -p * log p  -   (l-p) * log (1-p)

相对熵:KL散度

对于开机 :假如有2种结果,要么开机 要么死机. 用相对熵来衡量这两个熵的差异.

逻辑回归二分类实战

#逻辑回归实战
import  matplotlib.pyplot  as  plt
import   numpy  as  np

np.random.seed(0)
Num=100

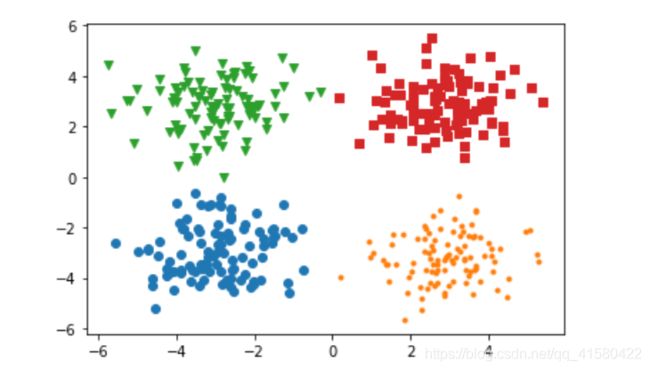
#X(x1 , x2)   y=0/1

#y=1 , 类别1 ,构建以(6,3 )  为中心的100个离散点
x1=np.random.normal( 6,1,size=(Num) )  #生成100个均值为 6 ,方差为1 的数组
x2=np.random.normal( 3,1,size=(Num) ) #生成100个均值为 3 ,方差为1 的数组
y=np.ones(Num)  #构建100个全1数组

c1=np.array( [x1,x2,y] )     #这是三行100列  (3,100)


#y=0 ,类别0 ,构建以(3,6 )  为中心的100个离散点
x11=np.random.normal( 3,1,size=(Num) )
x21=np.random.normal( 6,1,size=(Num) )
y11=np.zeros(Num)  #构建100个全0数组

c0=np.array( [x11,x21,y11] )     #这是三行100列

#转置
c1=c1.T  #(100 ,3)
c0=c0.T

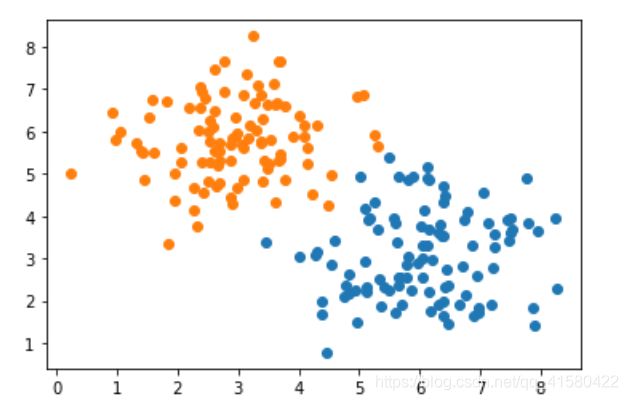
plt.scatter( c1[:,0], c1[:,1]   )
plt.scatter( c0[:,0], c0[:,1]   )

all_data=np.concatenate( (c1,c0) )    #两100x3  拼接到一起为200x3

#划分样本为训练集和测试集 如按3:1划分
#打乱all_data
np.random.shuffle(all_data)
train_data_x=all_data[ :150,:2]  #取all_data 前150个数据 ,每条数据的前2个值即 x1 ,x2
train_data_y=all_data[ :150,-1]

test_data_x=all_data[ 150:,:2]
test_data_y=all_data[ 150:,-1]

plt.scatter( c1[:,0], c1[:,1]   )
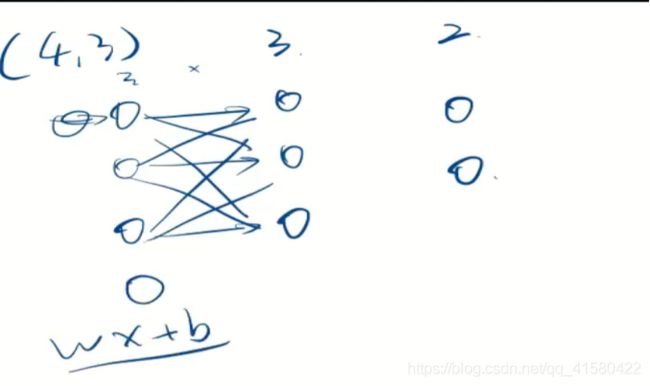
plt.scatter( c0[:,0], c0[:,1] ,marker='+'  )


w=np.random.rand(2,1)   #有两个参数w1 , w2 .  随机的初始化w ,      2行1列

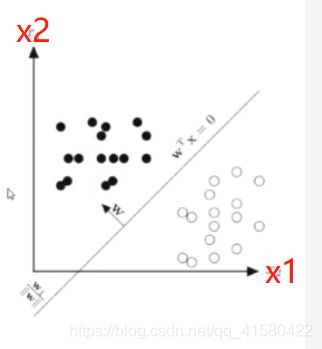
要学习的分类直线 wx = 0
.
下图可知x 是横坐标x1(常规坐标中的x) 与纵坐标x2(常规坐标中的y)的组合
.
要学习的分类直线 w1 * x1 + w2 * x2 = 0 (直角坐标系中用x与y 去描述这条分类线)

如果把x2看做是 常规中的y , 那么这条要学习的直线可表示为,

y = - w1 * x /w2

#随机初始化 要学习的 y = - w1 * x/  w2 
w=np.random.rand(2,1)   #有两个参数w1 , w2 .  随机的初始化w ,      2行1列

x= np.arange(10)
y=-( w[0] * x )/w[1]      
plt.plot(x,y)

#定义损失函数  交叉熵  : y是真实的值 ,y是预测的结果 
def cross_entropy(y,y_hat):
    return   -np.mean( y*np.log(y_hat)  + (1-y)*np.log(1-y_hat)  )

#y_hat = sigmoid(w * x)

def sigmoid(z):
    return 1./(1.+np.exp(-z) )

lr=0.001
for  i in range(100):
    y_hat=sigmoid(np.dot(w.T, train_data_x.T)  )
    #计算loss
    loss=cross_entropy(train_data_y,y_hat)

    #计算梯度   求平均(  x (真实值 -  预测值)  )
    grad= -np.mean(  (train_data_x* (train_data_y - y_hat).T ) ,  axis=0)

    #更新w
    w=w-(lr*grad).reshape(2,1)
    #输出
    if  i%10==1:
        print("i: %d , loss : %f"  %(i,loss ) )
    if  loss<0.1:
        break
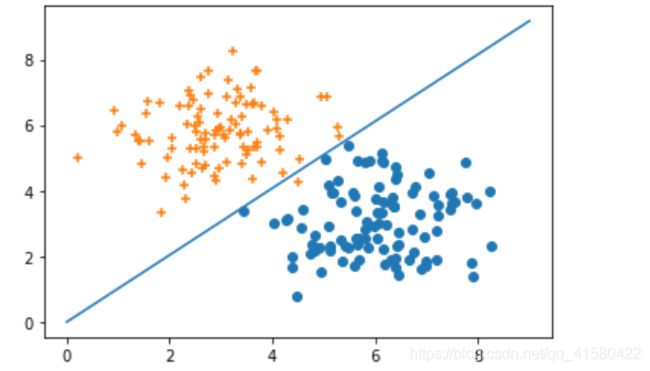
#y=w1 * x1 + w2 * x2 = 0
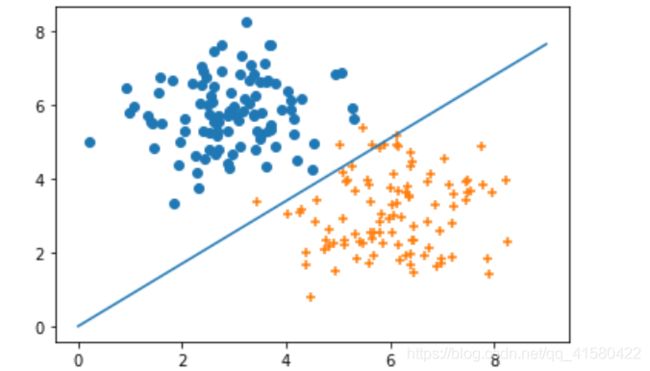
plt.scatter( c1[:,0], c1[:,1]   )
plt.scatter( c0[:,0], c0[:,1] ,marker='+'  )
x= np.arange(10)
y=-( w[0] * x )/w[1]
plt.plot(x,y)

#预测,查看测试集的准确率
#判断y=w1 * x1 + w2 * x2的值大于还是小于0

y_hat = np.dot(w.T,test_data_x.T)
y_pred= np.array(y_hat>0,dtype=int).flatten()
test_acc=np.sum(test_data_y==y_pred)/len(y_pred)  #准确率

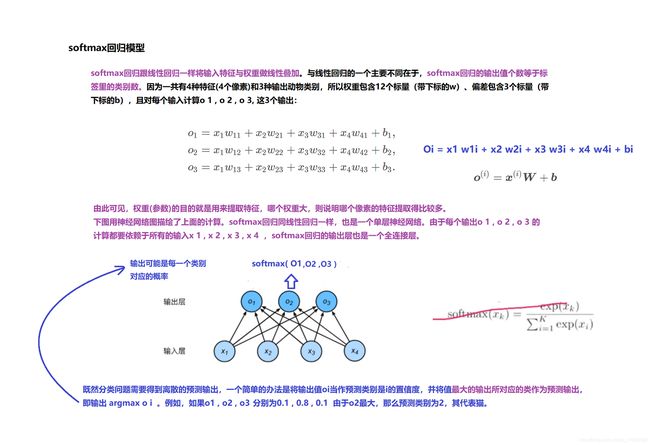
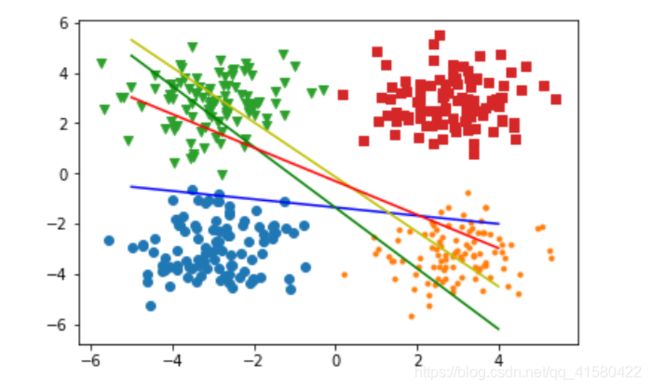
1.3 softmax回归

多分类

简单易懂的softmax讲解

#softmax多类别回归
#X(x1,x2)   y(0/1/2/3)
import  matplotlib.pyplot  as  plt
import   numpy  as  np

np.random.seed(0)
Num=100

#X(x1 , x2)  真实标签 y=0/1/2/3  <特征x1,x2分别对应着直角坐标系中的xy>  


#第0个类别数据  , 真实标签为0 的数据,   直角坐标系中是(-3 , -3)为中心的100个离散点
x1=np.random.normal( -3,1,size=(Num) )
x2=np.random.normal( -3,1,size=(Num) )
y=np.zeros(Num)
c0=np.array( [x1,x2,y] )    # 0分类


#第1个类别数据 ,真实标签为1的数据
x1=np.random.normal(  3,1,size=(Num) )
x2=np.random.normal( -3,1,size=(Num) )
y=np.ones(Num)
c1=np.array( [x1,x2,y] )    # 1分类

#第2个类别数据
x1=np.random.normal( -3,1,size=(Num) )
x2=np.random.normal( 3,1,size=(Num) )
y=np.ones(Num) * 2
c2=np.array( [x1,x2,y] )    # 2分类

#第3个类别数据
x1=np.random.normal( 3,1,size=(Num) )
x2=np.random.normal( 3,1,size=(Num) )
y=np.ones(Num)*3
c3=np.array( [x1,x2,y] )    # 3分类

#转置
c0=c0.T
c1=c1.T
c2=c2.T
c3=c3.T

plt.scatter( c0[:,0], c0[:,1]  ,marker='o')
plt.scatter( c1[:,0], c1[:,1]  ,marker='.')
plt.scatter( c2[:,0], c2[:,1]  ,marker='v')
plt.scatter( c3[:,0], c3[:,1]  ,marker='s')#marker是标识

#划分数据集并初始画线
all_data=np.concatenate( (c0,c1,c2,c3) )    #4个100x3  拼接到一起为400x3

#划分样本为训练集和测试集 如按3:1划分
#打乱all_data
np.random.shuffle(all_data)
train_data_x=all_data[ :300,:2]
train_data_y=all_data[ :300,-1].reshape(300,1)

test_data_x=all_data[ 300:,:2]
test_data_y=all_data[ 300:,-1].reshape(100,1)
#y=w1*x1+ w2*x2 +b      (一共有4个类别,所以 有两个偏执项 ,我们在直角坐标系中用x ,y这两个特征去描述类别 ,  所以4个类别有8个w的权值)

w=np.random.rand(4,2)   #4行2列
bias=np.random.rand(1,4)  #这是b,也称偏执像

plt.scatter( c0[:,0], c0[:,1]  ,marker='o')
plt.scatter( c1[:,0], c1[:,1]  ,marker='.')
plt.scatter( c2[:,0], c2[:,1]  ,marker='v')
plt.scatter( c3[:,0], c3[:,1]  ,marker='s')#marker是标识
x= np.arange(-5,5)   #画线
y1=-( w[0,0] * x +bias[0,0] )/w[0,1]
plt.plot(x,y1,'b')

y2=-( w[1,0] * x +bias[0,1] )/w[1,1]
plt.plot(x,y2,'g')

y3=-( w[2,0] * x +bias[0,2] )/w[2,1]
plt.plot(x,y3,'y')

y4=-( w[3,0] * x +bias[0,3] )/w[3,1]
plt.plot(x,y4,'r')

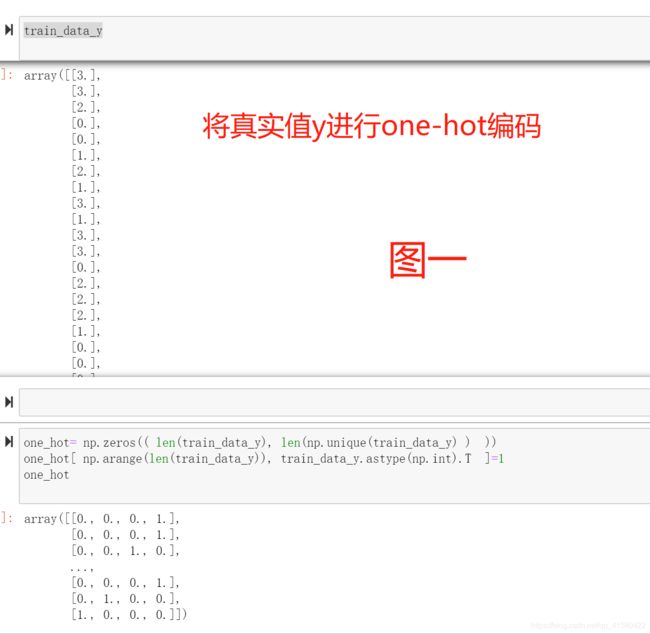
#真实值的y是一个值,     而预测输出的softmax(wx+b)是 每一个类别的概率 ,这里有4个类别,例如[  0.1  ,  0.2 , 0.7 , 0 ] ,所以对y应该采取同样长度的one-hot编码

#定义softmax(x)=e^x/sum(e^x)
def softmax(z):
    exp= np.exp(z)
    sum_exp=np.sum(np.exp(z),axis=1,keepdims=True )
    return  exp/sum_exp


#定义one-hot
#t例如 3    [0,0,1,0]代表3
def one_hot(temp):
    one_hot= np.zeros(( len(temp), len(np.unique(temp) )  ))
    one_hot[ np.arange(len(temp)), temp.astype(np.int).T  ]=1
    return one_hot

#计算wx+b
def compute_y_hat(w,x,b):
    return np.dot(x,w.T) +b

#计算交叉熵
def  cross_entropy(y,y_hat):
    return - (1/len(y))* np.sum(y*np.log(y_hat))
    #len(y) 是标签的长度 即 N ,   y是真实标签 ,  y_hat是预测值,softmax的出来的值


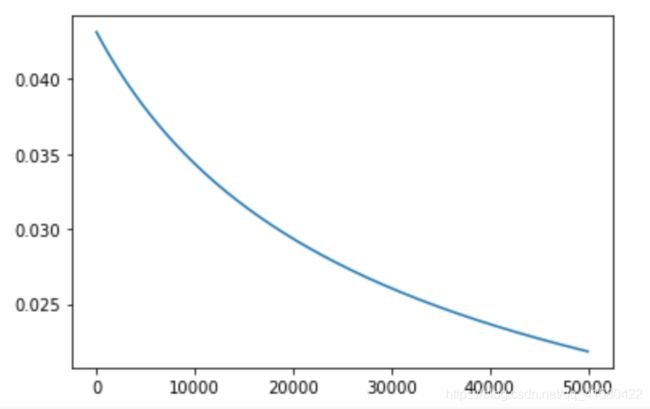
lr=0.001
all_loss=[]
for  i in range(10000):
    #计算loss
    x=train_data_x
    y=one_hot(train_data_y)   #看下图一  将所有的真实标签进行编码,也就是train_data_y的形状是(300,1)  ,生成对应的 (300 ,4)的one-hot编码 . 
    y_hat = softmax(compute_y_hat(w,x,bias))

    loss=cross_entropy(y,y_hat)
    all_loss.append(loss)

    #计算梯度
    grad_w= (1/len(X)) *np.dot(x.T,(y_hat - y))   
    grad_b= (1/len(X)) *np.sum(y_hat - y)    #b的梯度 : -1/N  * 求和( 真实值- 预测值)

    #更新w
    w=w-lr*grad_w.T
    bias=bias - lr*grad_b

    #输出
    if  i%100==1:
        print("i: %d , loss : %f"  %(i,loss ) )
    #if  loss<0.1:
     #   break
plt.plot(all_loss) #下图查看损失

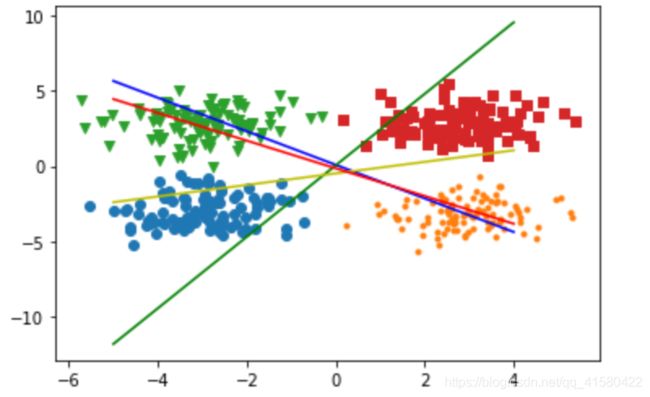
plt.scatter( c0[:,0], c0[:,1]  ,marker='o')
plt.scatter( c1[:,0], c1[:,1]  ,marker='.')
plt.scatter( c2[:,0], c2[:,1]  ,marker='v')
plt.scatter( c3[:,0], c3[:,1]  ,marker='s')#marker是标识
x= np.arange(-5,5)   #画线
y1=-( w[0,0] * x +bias[0,0] )/w[0,1]
plt.plot(x,y1,'b')

y2=-( w[1,0] * x +bias[0,1] )/w[1,1]
plt.plot(x,y2,'g')

y3=-( w[2,0] * x +bias[0,2] )/w[2,1]
plt.plot(x,y3,'y')

y4=-( w[3,0] * x +bias[0,3] )/w[3,1]
plt.plot(x,y4,'r')

#测试集预测
def  predict(x):
    y_hat=softmax(compute_y_hat(w,x,bias))
    return  np.argmax(y_hat,axis=1)
#计算模型在测试上的准确率
np.sum(  predict(test_data_x).reshape(100,1)==test_data_y )  /len(test_data_y)

1.4 感知器

线性分类器,二分类

更多知识: 感知器的收敛性与其证明 / 参数平均感知器/多分类应用

#感知器实战
import  matplotlib.pyplot  as  plt
import   numpy  as  np

np.random.seed(0)
Num=100

#X(x1 , x2)   y= -1 /1
#y=-1类
x1=np.random.normal( 6,1,size=(Num) )
x2=np.random.normal( 3,1,size=(Num) )
y=np.ones(Num) *-1  #构建100个全1数组
c0=np.array( [x1,x2,y] )     #这是三行100列, #-1分类

#y=1类
x1=np.random.normal( 3,1,size=(Num) )
x2=np.random.normal( 6,1,size=(Num) )
y=np.ones(Num)  #构建100个全0数组
c1=np.array( [x1,x2,y] )     #这是三行100列  #1分类

#转置
c0=c0.T
c1=c1.T

plt.scatter( c0[:,0], c0[:,1]   )
plt.scatter( c1[:,0], c1[:,1]   )

#划分数据及
all_data=np.concatenate( (c1,c0) )    #两100x3  拼接到一起为200x3

#划分样本为训练集和测试集 如按3:1划分
#打乱all_data
np.random.shuffle(all_data)
train_data_x=all_data[ :150,:2]
train_data_y=all_data[ :150,-1].reshape(150,1)

test_data_x=all_data[ 150:,:2]
test_data_y=all_data[ 150:,-1].reshape(50,1)

w=np.zeros((2,1))   #2行1列
T=100
K=0
train_data=np.concatenate( (train_data_x,train_data_y),axis=1 )


#训练模型
for t  in  range(T):
    np.random.shuffle(train_data)  #随机打乱样本
    for i  in range( len(train_data) ):

        #选择第i个样本
        gloss= np.dot(w.T,( train_data[i][-1] * train_data[i][:2]).reshape(2,1) )[0,0]
        if gloss<=0:
            w=w+( train_data[i][-1] * train_data[i][:2] ).reshape(2,1)

plt.scatter( c1[:,0], c1[:,1]   )
plt.scatter( c0[:,0], c0[:,1] ,marker='+'  )
x= np.arange(10)
y=-( w[0] * x )/w[1]
plt.plot(x,y)
#结果大部分,绝大部分的点被分开了,少部分点没有分开是因为取的训练集的数目是2/3,没有包含所有的点,虽然感知机的原理是使所有的点满足 ywx > 0 ,但是下面的点也不是完全意义上的线性可分.

1.5 支持向量机

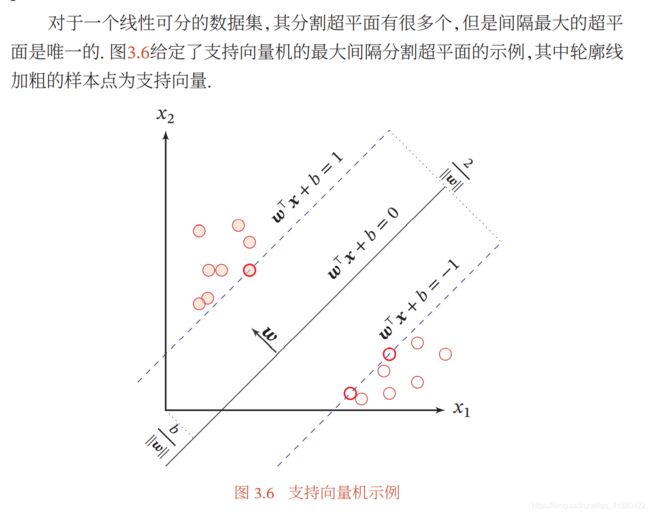
支持向量机原理(一) 线性支持向量机

支持向量机（SVM）——原理篇

下面就属于数学方法去求解这个条件和目标了
要解决就用到拉格朗日乘子法:

软间隔

到这里都是基于训练集数据线性可分的假设下进行的，但是实际情况下几乎不存在完全线性可分的数据，为了解决这个问题，引入了“软间隔”的概念，即允许某些点不满足约束

支持向量机原理(二) 线性支持向量机的软间隔最大化模型

核函数

线性可分SVM通过软间隔最大化，可以解决线性数据集带有异常点时的分类处理，但是现实生活中的确有很多数据不是线性可分的，这些线性不可分的数据也不是去掉异常点就能处理这么简单。那么SVM怎么能处理中这样的情况呢？

支持向量机原理(三)线性不可分支持向量机与核函数

以上,支持向量机就结束了,遗留SMO算法原理
支持向量机原理(四)SMO算法原理
支持向量机在回归模型的应用
支持向量机原理(五)线性支持回归

除去上面的复杂的求解过程和思想,支持向量机的最原始本质是(个人感觉记住下面这个就可以了,上面的复杂的用到再说)

1.6 总结

…

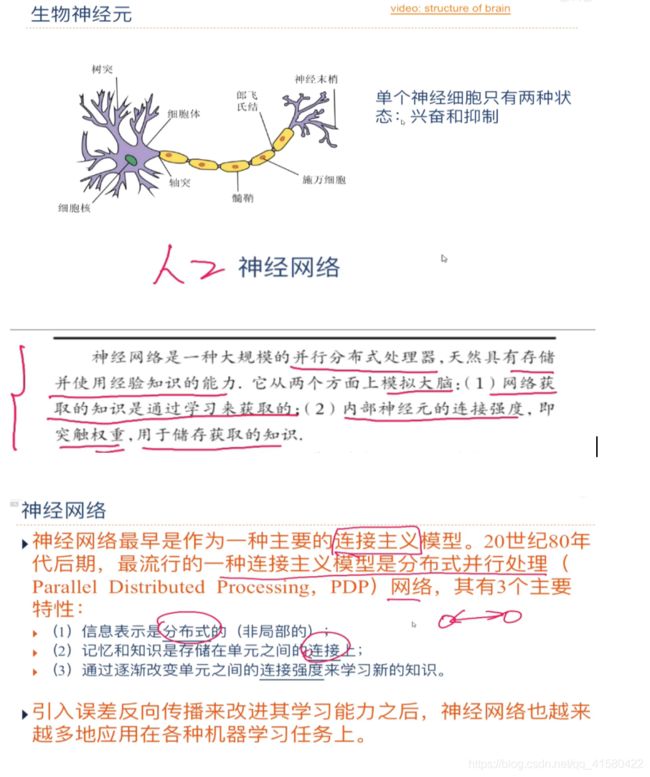
场景六:神经网络

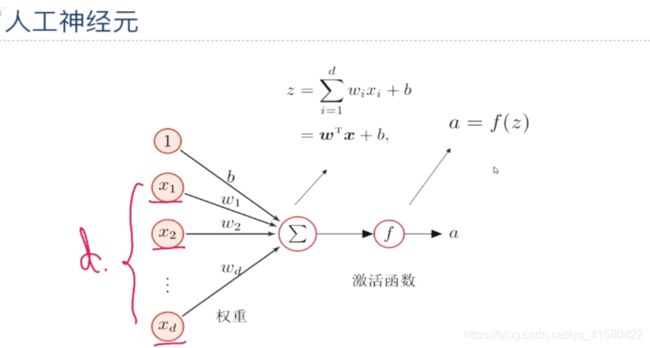
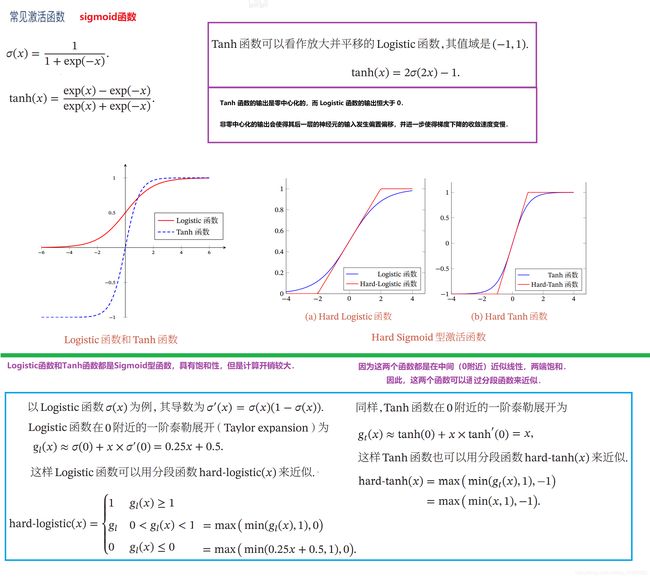
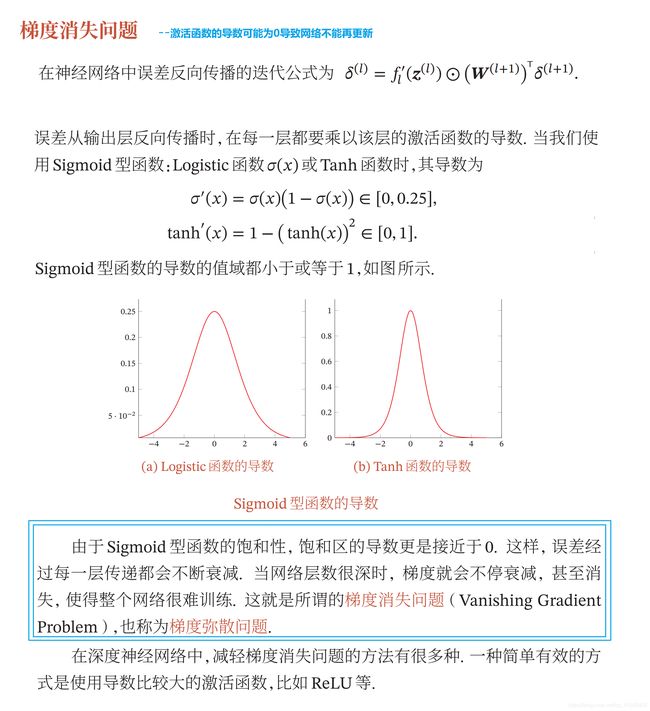
1.1 基础介绍与常见激活函数

> 1: 其中激活函数尽量要连续、非线性、可导  (可导的激活函数可以直接利用数值优化的方法学习参数  <学习参数方便> ) ; 
> 2: 激活函数及其导数还需要尽可能的简单，有利于提高网格计算效率.
> 3: 激活函数的导函数值域应该在一个合适的范围内。(不能太大也不能太小，否则会影响训练的效率和稳定性．)

sigmoid 型激活函数

logistic函数 / Tanh函数 —> Hard-Logistic函数/ Hard-Tanh函数

ReLU 函数

Swish 函数

GELU 函数

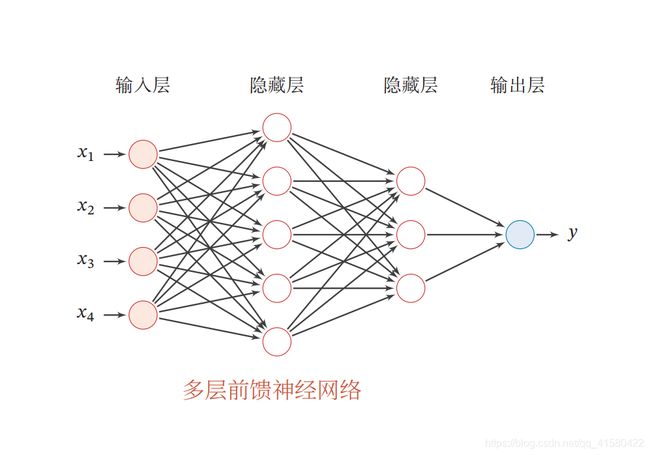
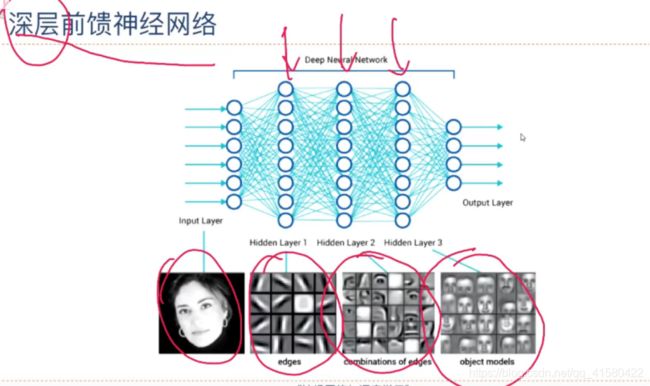
1.2 前馈神经网络

通用近似定理

前馈神经网络具有很强的拟合能力，常见的连续非线性函数都可以用前馈神经网络来近似．
通用近似定理在实数空间ℝ 中的有界闭集上依然成立． (通用近似定理有极限那味了)

应用原理

参数学习理论

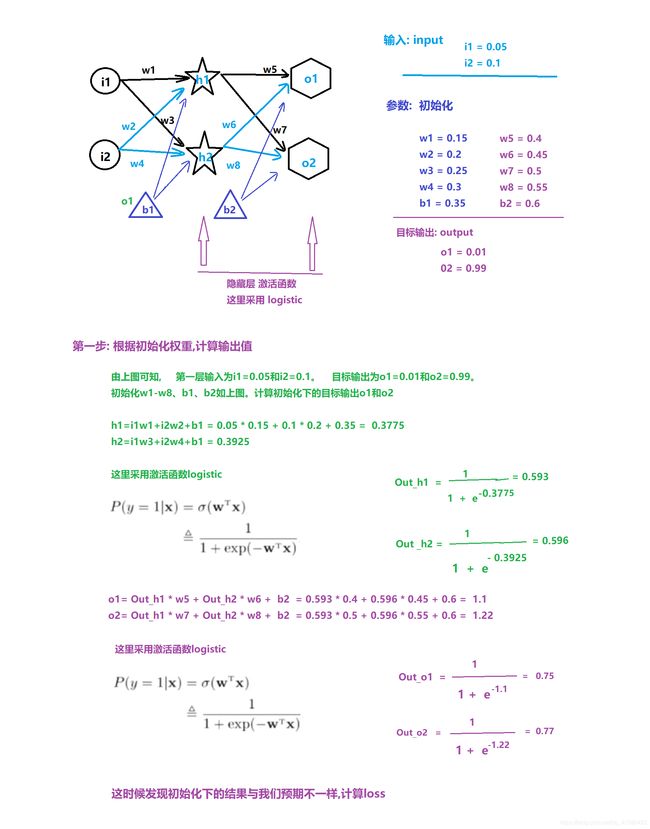
1.3 反向传播算法

1.4 自动梯度计算

.
重点后续内容参考–>场景七: 基于tensorflow的自动梯度计算

数值微分

符号微分

自动微分–>(相对重点)

重点内容–>参考<场景七: 基于tensorflow的自动梯度计算>

1.5 神经网络进行参数学习的难点

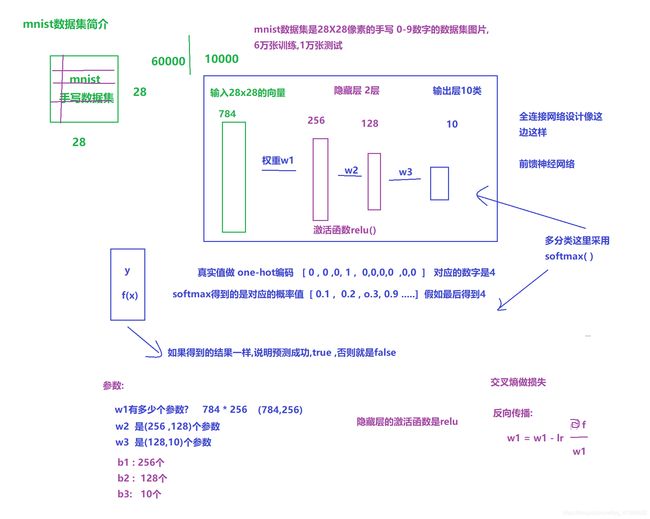
1.6 前馈神经网络对MNIST数据集的分类

–>先学完场景七的内容再回头看看这个主题

import tensorflow as tf
import matplotlib.pyplot as plt

#28x28的输入层h0  784
#两个隐藏层h1：256   h2：128
#输出层h3：10

#第一步: 初始化参数
w1=tf.Variable(tf.random.truncated_normal([784,256],stddev=0.1))
w2=tf.Variable(tf.random.truncated_normal([256,128],stddev=0.1))
w3=tf.Variable(tf.random.truncated_normal([128,10],stddev=0.1))


b1=tf.Variable( tf.zeros([256]) )
b2=tf.Variable( tf.zeros([128]) )
b3=tf.Variable( tf.zeros([10]) )




#第二步: 加载数据集,tf.keras.datasets中提供了加载mnist数据集的api

(x_train,y_train),(x_test,y_test)  =tf.keras.datasets.mnist.load_data(path='mnist.npz')  #这里会下载这个数据集

代表6万张28X28的图片 y代表对应的6万张图片对应的0-9的结果。

x_train = tf.convert_to_tensor(x_train, dtype=tf.float32) / 255.
y_train = tf.convert_to_tensor(y_train, dtype=tf.int32)

# 转换为(60000,784)

x_train = tf.reshape(x_train, [-1, 28 * 28])
# -1代表任意多个值  这个时候的x_train已经是60000*784   这个时候就转换为tensor的数组了




# 第三步: 根据自己设计的网络完成前向计算

# h1;net1(z=sum(wx+b))    out1(relu(z))
# [60000,784]@[784,256] +[256]
# net1= x_train@w1 + tf.broadcast_to(b1,[x_train.shape[0],784]  )
net1 = x_train @ w1 + b1
out1 = tf.nn.relu(net1)


# h2;net2( z=sum(wx+b))    out2(relu(z))
# [60000,256]@[256,128] +[128]
# net2= x_train@w1 + tf.broadcast_to(b2,[x_train.shape[0],256]  )
net2 = out1 @ w2 + b2
out2 = tf.nn.relu(net2)


# h3;net3( z=sum(wx+b))    out3(relu(z))
# [60000,256]@[128,10] +[10]
# net2= x_train@w1 + tf.broadcast_to(b2,[x_train.shape[0],128]  )
net3 = out2 @ w3 + b3
out3 = tf.nn.softmax(net3)





#第四步: 进行反向传播更新参数

# 进行one_hot编码
y_train = tf.one_hot(y_train, depth=10)

loss = tf.nn.softmax_cross_entropy_with_logits(labels=y_train, logits=out3)

loss = tf.reduce_mean(loss)

lr = 0.01

All_loss = []
for step in range(10001):
    with tf.GradientTape()  as    tape:
        tape.watch([w1, b1, w2, b2, w3, b3])

        # 构建跟踪过程
        out3 = tf.nn.softmax(tf.nn.relu(tf.nn.relu(x_train @ w1 + b1) @ w2 + b2) @ w3 + b3)
        loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y_train, logits=out3))

    All_loss.append(loss)
    grads = tape.gradient(loss, [w1, b1, w2, b2, w3, b3])

    # 更新参数:
    w1.assign_sub(lr * grads[0])
    b1.assign_sub(lr * grads[1])
    w2.assign_sub(lr * grads[2])
    b2.assign_sub(lr * grads[3])
    w3.assign_sub(lr * grads[4])
    b3.assign_sub(lr * grads[5])

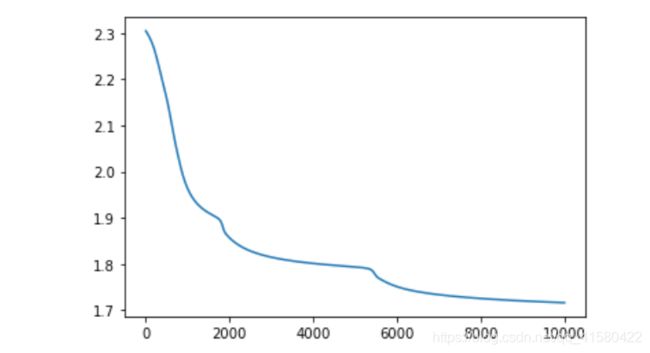
    if step % 50 == 0:
        print('step{}:   loss:{} '.format(step, loss))  # 在这里{}是占位符
plt.plot(All_loss)

#预测模型
x_test =tf.convert_to_tensor(x_test,dtype=tf.float32)/255.
y_test =tf.convert_to_tensor(y_test,dtype=tf.int32)
x_test= tf.reshape(x_test,[-1,28*28]) 

out3=tf.nn.softmax( tf.nn.relu(tf.nn.relu( x_test@w1 + b1)@w2 + b2)@w3 + b3)

y_predict = tf.math.argmax(out3,axis=-1)

y_test=tf.cast(y_test,tf.int64)

y_c=tf.math.equal(y_predict,y_test)

y_c =tf.cast(y_c,tf.int64)
r=tf.math.reduce_sum( y_c )/10000
r.numpy()  #准确率

#batch  size
batchDataset  =  tf.data.Dataset.from_tensor_slices(   (x_train,y_train) ).batch(128)
train_iter= iter(batchDataset)
sample=next(train_iter)

…

场景七:TensorFlow2.0

tensorflow的官方API查询

tensorflow安装参考场景二

1.1 基于tensorflow的自动梯度计算—>对目标参数求导数

jupyte使用小技巧

$y=w1* x^2 + w2*x  +b $
$\frac {dy}{dx}=2w1*x+w2$  #$的使用会让代码加粗并变为数学格式
$y=\frac{1}{1+e^{-x} } $

shift+ tab键  可以查看jupyter的中写的方法的用法

对目标参数求导

import tensorflow  as tf
w1 = tf.constant(1.)   #定义一个常数
w2 = tf.constant(2.)
b = tf.constant(3.)
x = tf.constant(4.)


# 开始求梯度,即x=4的时候,对应的导数值
# 构建一个梯度环境
with tf.GradientTape()  as    tape:
    tape.watch(x)  # 因为要对x进行求梯度,所以把x加入跟踪列表
    
    # 构建跟踪过程
    y = w1 * (x ** 2) + w2 * x + b
    dy_dx = tape.gradient(y, x) 
    # 表示对x=4时候的导数值    dy_dx = 2 w1*x1 + w2 = 的结果为10.0

import tensorflow  as tf

w = tf.constant(1.)
b = tf.constant(3.)
x = tf.constant(4.)
# 开始求梯度,即x=4的时候,对应的导数值

# 构建一个梯度环境
with tf.GradientTape()  as    tape:
    tape.watch([w, b])  # 因为要对w,b进行求梯度,所以把w,b加入跟踪列表
    # 构建跟踪过程
    y = w * x + 3 * b

    dy_dw, dy_db = tape.gradient(y, [w, b])
    # 表示对w=1时候对w的导数值    dy_dw的结果为4.0
      表示对b=3时候对b的导数值    dy_db的结果为3.0

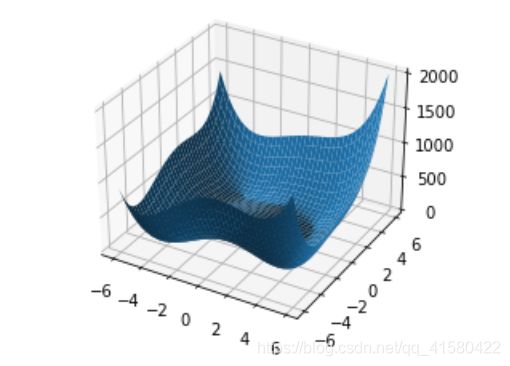
应用:Himmelblau函数优化求局部最小值

himmelblau函数是数学家们构造出来的一个特殊的函数，可以用来测试深度学习算法是否能够收敛到局部最小值

>>1: 引入头

#找局部最小
import tensorflow as tf
import numpy  as  np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

>>2: 绘制himmelblau函数的图像

def himmelblau(x):
    # x x[0],x[1]代表x,y
    return (x[0] ** 2 + x[1] - 11) ** 2 + (x[0] + x[1] ** 2 - 7) ** 2

# 先把这个图画出来
x = np.arange(-6, 6, 0.1)  # x.shape 为(120,)
y = np.arange(-6, 6, 0.1)  # y.shape 为(120,)

X, Y = np.meshgrid(x, y)

z = himmelblau([X, Y])  # x[0]就是X,x[1]就是Y

fig = plt.figure('himmelblau')
ax = fig.gca(projection='3d')
ax.plot_surface(X, Y, z)
plt.show()

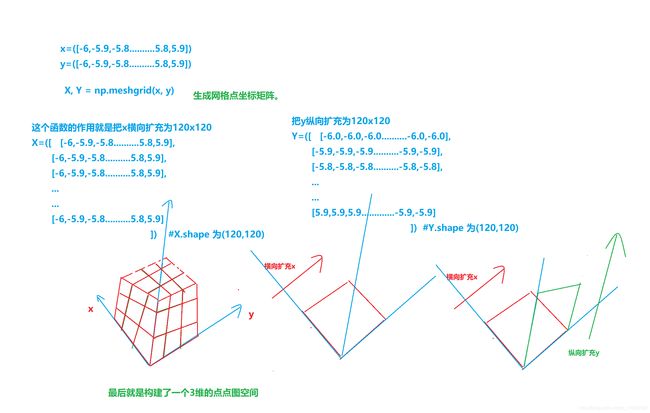
可能这里这个函数理解有误,更多详细请看:
numpy.meshgrid()理解

Python-Numpy模块Meshgrid函数

np.mgrid(),np.meshgrid()与三维画图

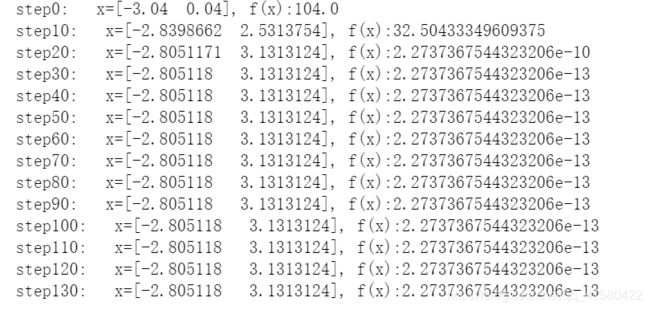
>>3: 初始化函数himmelblau 并梯度下降

x = tf.constant([4., 0.0])

lr = 0.01

for step in range(140):
    with tf.GradientTape()  as    tape:

        tape.watch(x)
        # 构建跟踪过程
        y = himmelblau(x)

        grads = tape.gradient(y, x)
    x = x - lr * grads
    if step % 10 == 0:
        print('step{}:   x={}, f(x):{} '.format(step, x, y))  # 在这里{}是占位符

当4的时候,周围局部最小是3.5附近的 -1.85
.
再如当-3的时候如下,和实际差不多。

1.2 基本操作

import  tensorflow   as tf

# 可以查看tensorflow的版本 
 tf.__version__

变量和张量

>>变量的创建与简单操作

#定义变量

#在其他语言中 , 如我们定义变量   int a = 1 ;   int a ; a=1 等,a是变量
#在tensorflow中,定义变量的语法为:       
a=tf.Variable(1)     # tf.Variable()中的1是变量a的值
a=tf.Variable(1.0)   

为什么要创建一个tensorflow的变量?
通过这个方法创建的变量是一个可以训练的变量,这个变量是可以求梯度的.(在前面的全神经网络中,w b的值就是这样定义的)

>>张量的定义与简单操作

张量tensor 作为tensorflow数据的基本单位 相当于多维数组,
dim代表维度
当dim=0的时候 0维代表是一个数 1,2,3
当dim=1的时候 1维代表是一个向量 [1,2,3,4]
当dim=2的时候 2维就是一个数组 [ [ 1,2 ], [3,4] ]

tf.constant(1)     #定义了一个tensor类型的数  1
tf.constant(1.1)   #定义了一个tensor类型的浮点数  1.1
tf.constant( 1.1, dtype= tf.float32  )    
#或者指定数据类型,不过float32要匹配前面的1.1, 而且还一定要是tf.float32

tf.constant('hello' )     #可以是字符串
tf.constant(True )        #可以是boolean类型
tf.constant( [1,2,3,4]  ) #可以是一个数组

tf.range(10)   #还可以定义一个tensorflow有范围的张量数组

为什么要使用张量?
因为可以方便把张量放在cpu上算,也可以放在gpu上算.

a=tf.range(10)    
aa=a.cpu()         # aa =a.gpu() 默认是gpu上算
aa.device

有时候tensor的数组张量和numpy的数组会在一个程序中,但是不能共同运算.

#判断是否是tensor
tf.is_tensor(a)
#isInstance(a, tf.Tensor)

#查看数组的维度
a.ndim
#tf.rank(a)    

#查看数组的形状
a.shape, 
a.shape[0],  a.shape[1]

#改变尺寸
a=tf.reshape( tf.range(10),[2,5] ) #定义一个2行5列的0-10的数组



# 全0的张量
tf.zeros([2, 3])

# 全1的张量
a = tf.ones([4, 3])

# 构建一个像a形状一样的全0/1张量b
b = tf.zeros_like(a)  # ones_like



# 填充
tf.fill([5, 7], 3.0)  # 用3.0构建5X7的张量

# 填充一个随机值
tf.random.normal([5, 7])
tf.random.normal([5, 7], stddev=2, mean=5)  # 以5为主心随机生成的5行7列的 正太分布数

tf.random.truncated_normal([3, 5])  # 两端趋于0的时候  给截断掉  可以解决梯度消失的问题




#tensorflow的索引和切片
v=tf.Variable( [1,2,3,4] )
v[0]   # 结果为: 

a=tf.Variable(tf.reshape (tf.range(10),[2,5])  )
a[1][3]   #结果为

a[:,2]   #切片结果为

1.3 tensorflow基础数学计算库

#不同参数的相加
tf.add(1,2)
tf.add(  [1,2] ,[3,4] )  #结果为   

#同一个参数中 降维度相加  
tf.reduce_sum( [1,2,3] )              #结果为6   1维降为0维
tf.reduce_sum([ [1,2,3],[4,5,6] ])  #结果为21   2维降为0维   

tf.reduce_sum([  [1,2,3],  [4,5,6]   ], axis=0 )  #第0维度代表列加,结果为([5,7,9])
tf.reduce_sum([  [1,2,3],  [4,5,6]   ], axis=1 )  # 第二维度代表行,  结果为([6,15])  

#求平均
tf.reduce_mean( [4, 6] )   #结果为 

#矩阵的乘法
a=tf.constant ([ [1] ])    #a是 1x1
b=tf.constant([  [2,3]  ])  #b是1X2   目标axb

c=tf.matmul(a,b)   #等价于  c=a@b

#numpy和tensor的相互转换
#a由上面可知是一个tensor类型
b=a.numpy()   #tensor装换为numpy
tf.convert_to_tensor( b)  #用tensorflow的方法实现numpy转换为tensor

1.4 进阶操作

tf.concat( ) 拼接

#张量的拼接
import  tensorflow   as tf
t1=tf.constant([  [1,2,3],[4,5,6]  ])
t2=tf.constant([  [1,2,3],[4,5,6]  ])

tf.concat(  [t1,t2] ,axis=0 )  #第一维度上做拼接
tf.concat(  [t1,t2] ,axis=1 )  #第二维度上做拼接

tf.split( ) 拆分

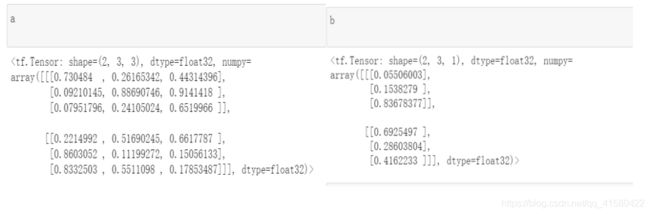
#等份拆分
a,b=tf.split(img_stack,axis=2,num_or_size_splits=2)

#按比例拆分
a,b=tf.split(img_stack,axis=2,num_or_size_splits=[3,1])

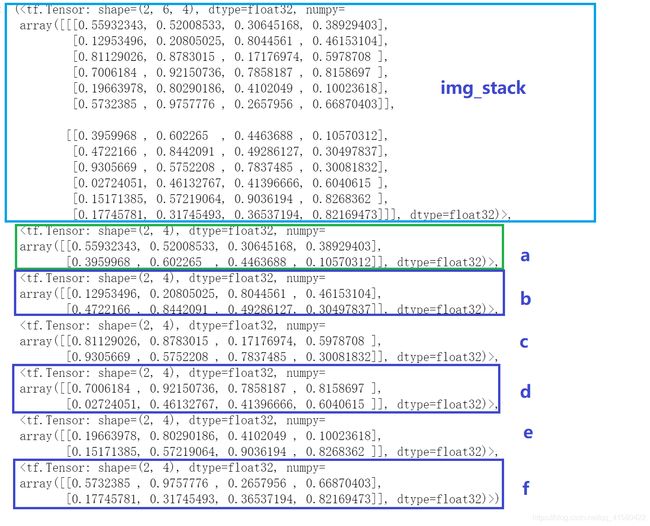
tf.satck ( ) / tf.unstack ( )

每个图片是(6,4),现在有两张图片,我想把图片这两张叠加在一起变为(2,6,4)的格式

>>叠加在axis=0上 ,分别在axis=0和axis=1上拆分

#数据叠加与拆分
import  tensorflow   as tf
import  matplotlib.pyplot  as  plt

img1 = tf.random.uniform( [6,4])
img2 = tf.random.uniform( [6,4])


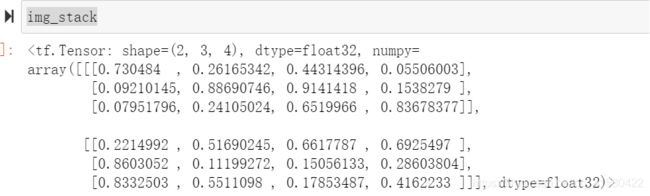
#在第一维度上进行两张图片的叠加
img_stack = tf.stack( [img1,img2],axis=0 )
img_stack.shape    #结果为TensorShape([2, 6, 4])
plt.matshow(img_stack)  #下面为叠加效果

#对img_stack在第一维度上拆分发现会变为原来的图像,注意拆分后的形状
a,b=tf.unstack(img_stack,axis=0)
a.shape  #结果为TensorShape([6, 4])
b.shape  #结果为TensorShape([6, 4])
plt.matshow(a)
plt.matshow(b)

#axis=1上拆分,    (2 ,6 ,4)--->变为  6个(2,4)
a,b,c,d,e,f=tf.unstack(img_stack,axis=1)

a.shape  #结果为TensorShape([2, 4])
b.shape  #结果为TensorShape([2, 4])
c.shape  #结果为TensorShape([2, 4])
d.shape  #结果为TensorShape([2, 4])
e.shape  #结果为TensorShape([2, 4])
f.shape  #结果为TensorShape([2, 4])

#img_stack = tf.stack( [a,b,c,d,e,f],axis=1 ) 可以再合并

>>叠加在axis=1上 ,分别在axis=0和axis=1上拆分

#在第二维度上进行两张图片的叠加
img_stack = tf.stack( [img1,img2] ,axis=1 )
img_stack.shape  #(6,2,4)
img1,img2,img_stack 

#第一维度上拆分,axis=0,因为是( 6,2,4 ),所以一维度上拆分是6个参数
a,b,c,d ,e,f=tf.unstack(img_stack,axis=0)
a.shape   #(2,4)

#第二维度上拆分,axis=1,因为是( 6,2,4 ),所以二维度上拆分是2个参数
a,b=tf.unstack(img_stack,axis=1)
a.shape   #(6,4)

tf.expand_dims( )

由上面可知,我们进行数据的叠加的时候,会添加数据的维度.如上面的(6,4)–>变为了(2,6,4) 或者在第二维度叠加变为(6,2,4) .当然我们也可以输入多个参数从而达到叠加到(n,6,4)的效果.
.
但如何让( 6,4 ) -->(1,6,4)或者(6,1,4)?

a = tf.random.normal( [6,4] )     #例如a的形状是(6,4)
b = tf.expand_dims( a , 0)        #b的形状是(1 , 6 ,4 )

a = tf.random.normal( [6,4] )    #例如a的形状是(6,4)
b = tf.expand_dims( a , 1)       #b的形状是(6 ,1,4 )

数据统计/范数

#数据统计
import  tensorflow   as tf

#向量的范数   
x=tf.constant([ [1.,2.],[3.,4.]  ])

#1范数
tf.norm(x, ord=1)   #ord表示几范数  结果为10.0
tf.norm(x, ord=1,axis=0)  #结果为  numpy=array([4., 6.], dtype=float32)
tf.norm(x, ord=1,axis=1)  #结果为  numpy=array([3., 7.], dtype=float32)

#2范数
tf.norm(x, ord=2)    #结果为5.477226   (1x1+2X2 +3x3 +4x4)开根号
tf.norm(x, ord=2,axis=0)    #结果为array([3.1622777, 4.472136 ], dtype=float32)
tf.norm(x, ord=2,axis=1)    #结果为array([2.236068, 5.      ],dtype=float32)

#无穷范数
tf.norm(x, ord=np.inf)       #向量的正无穷范数  结果为4.0

#求最小
tf.reduce_min(x) #结果为1.0
tf.reduce_min(x,axis=0)  #结果为 numpy=array([1., 2.], dtype=float32)
tf.reduce_min(x,axis=1) #结果为 numpy=array([1., 3.], dtype=float32)

#求最大
tf.reduce_max(x) #结果为4.0
tf.reduce_max(x,axis=0)  #结果为numpy=array([3., 4.], dtype=float32)
tf.reduce_max(x,axis=1)  #结果为numpy=array([2., 4.], dtype=float32)

#数据类型的转换
tf.cast(x, dtype, name=None)
第一个参数 x:   待转换的数据（张量）
第二个参数 dtype： 目标数据类型
第三个参数 name： 可选参数，定义操作的名称

#作比较,是否相等
a=tf.constant([1,2,3,4,5])
b=tf.constant([2,2,3,3,5]) 
tf.equal(a,b)   #结果为 numpy=array([False,  True,  True, False,  True])

z=tf.equal(a,b)
z=tf.cast(z,dtype=tf.int32)  #结果为numpy=array([0, 1, 1, 0, 1])

#数据统计
tf.reduce_sum(z)  #结果为3

张量在边界的填充

#张量的填充  

#例如 123456  变8位    填充12345600  或者00123456 01234560
#方法 tf.pad(x, paddings)      
#padding填充规则 [  [第一维度左边,第一维度右边], [第二维度左边,第二维度右边],  [第三维度左边,第三维度右边]    ]


a=tf.constant( [1,2,3,4,5,6] )
b=tf.constant(   [7,8,1,6]   )

#单维填充
#例如b在6的后面填充两个0   ,b只有一个维度 ,不指定参数默认填充0
b=tf.pad(b, [ [0,2] ] )  #第一维度左边不填充,右边填充2个0  结果为numpy=array([7, 8, 1, 6, 0, 0])
b=tf.pad(b, [ [2,0] ] )  #左边边再填充两个0  结果为numpy=array([0, 0, 7, 8, 1, 6, 0, 0])

#多维度填充
x=tf.constant([ [1,2,3],[4,5,6] ])

b=tf.pad(x,[[2,1],[0,0] ])

  '''
  结果为
  array([[0, 0, 0],
        [0, 0, 0],
        [1, 2, 3],
        [4, 5, 6],
        [0, 0, 0]])
  '''

b=tf.pad(x,[[1,1],[1,1] ])  

  '''
  array([[0, 0, 0, 0, 0],
        [0, 1, 2, 3, 0],
        [0, 4, 5, 6, 0],
        [0, 0, 0, 0, 0]])
  '''

填充应用

#案例 数据处理填充
#MNIST
#IMDB
total_words = 10000
max_review_len =80
embedding_len =100

#加载IMDB数据集
(x_train,y_train),(x_test,y_test) = tf.keras.datasets.imdb.load_data()

len(x_train[0]), len(x_train[1]), len(x_train[2])  #结果为(218, 189, 141) 发现每一个句子的长度都不一样
#例如我们要截断取值 长度为80,不够80补0
x_train=tf.keras.preprocessing.sequence.pad_sequences(x_train,maxlen=max_review_len,truncating='post'  ,padding='post' )

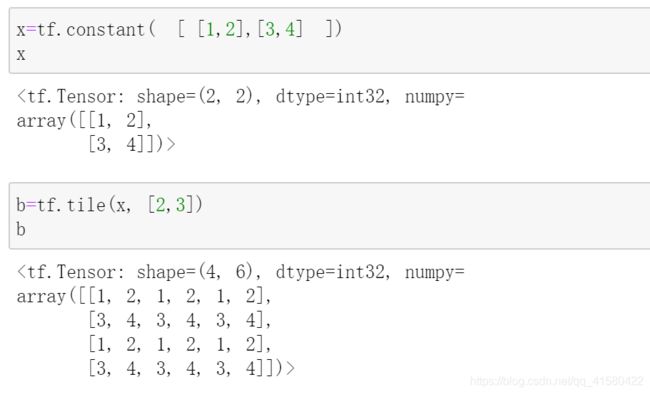
指定放大形状的倍数

#复制 tile()  可以指定放大形状的倍数
x=tf.random.normal([4,28,28,3])     #x.shape是(4, 28,28,3  )
x=tf.tile(x, [2,3,1,2])
x.shape  #结果为TensorShape([8, 84, 28, 6]),对应位置分别扩大2,3,1,2倍

b=tf.costant( [ 1,2 ],[3,4]  )   b的形状为(2,2)
b=tf.tile(b, [2,3]    )
b.shape  #结果为(4,6)

数据的限浮 区间[a,+无穷]

#数据限浮  tf.maximum(x,a)  [a,+...]  minimum(-...,a]
#例如数据原来是([ 1,2,3,5,6,7,8])  要取对应的3-8  还要使得1、2变为3

x=tf.constant([1,2,3,5,6,7,8])
x=tf.maximum(x,3)  #结果为array([3, 3, 3, 5, 6, 7, 8])
x=tf.minimum(x,7)  #结果为array([3, 3, 3, 5, 6, 7, 7])
tf.clip_by_value(x,5,7) #结果为 numpy=array([5, 5, 5, 5, 6, 7, 7])

tf.gather() 收集☆☆☆

#索引取样
#tf.gather()  收集
#举例子,一共有4各班级,每班35名学生,每个班级有8门课,这时候[4,35,8]的张量
x=tf.random.uniform( [4,35,8],maxval=100, dtype=tf.int32 )  #uniform随机生成  成绩最大值为100
x1=tf.gather(x,[0,1],axis=0)  #代表第一维度上 取前两个班级的成绩

#收集每个班级第五名,第8名,第9名的成绩
tf.gather(x,[4,7,8], axis=1 )
'''
array([[[92, 56, 36, 26, 77, 80, 78, 40],
        [59,  4, 77, 17, 66, 21, 19, 74],
        [34,  8, 51, 34, 85, 53, 66, 56]],

       [[ 2, 46, 60, 53, 98, 50, 23, 53],
        [ 9, 92, 14, 25, 80, 51, 31, 78],
        [29, 44, 55, 38, 61, 68, 87, 16]],

       [[11, 57, 99, 98, 43, 45, 79, 10],
        [82, 70, 12, 28, 39, 61, 79, 50],
        [29, 62,  9,  3, 38, 34, 46, 96]],

       [[ 0, 10,  0, 61, 87, 61, 86, 43],
        [35,  9, 46, 16, 65, 64,  5, 86],
        [16, 80, 91, 43, 31, 78, 65, 47]]])
'''
#收集同学的第三门的,第五门的成绩
tf.gather(x,[2,4], axis=2)

#抽查第2,3班的[3,4,5,6]的成绩
x1=tf.gather(x,[1,2],axis=0)  #先取到班级
tf.gather(x1,[2,3,4,5], axis=1 )  #然后取人

#抽查第二班的2号,3好班的三号的成绩
#x[1,1]  x[2,2]
#第一种方法
tf.stack([   x[1,1] ,x[2,2]  ],axis=0 )

#第二种做法
tf.gather_nd(x, [[1,1],[2,2] ] )

#抽查第二班的2号,3好班的三号的第1学科成绩
#x[1,1,1]  x[2,2,1]
#第一种方法
tf.stack([   x[1,1,1] ,x[2,2,1]  ],axis=0 )

#第二种做法
tf.gather_nd(x, [[1,1,1],[2,2,1] ] )

tf.boolean_mask()

#掩码取样
#tf.boolean_mask(),上面的tf.gather进行取样是通过索引号,除此以外还可以通过掩码形式取样


import  tensorflow   as tf
#举例子,一共有4各班级,每班35名学生,每个班级有8门课,这时候[4,35,8]的张量
x=tf.random.uniform( [4,35,8],maxval=100, dtype=tf.int32 )  #uniform随机生成  成绩最大值为100

mask=[True,False,False,True]   #掩码的长度一定要注意
tf.boolean_mask(x,mask, axis=0) #相当于取了第1个和第四个班级  

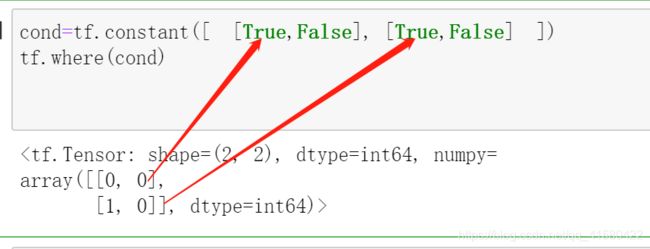
tf.where(cond,x,y)

#条件取样
#tf.where(cond,x,y)  #cond表示条件,条件为真取x对应位置的值   假取y对应位置的值
a=tf.ones([2,2])
b=tf.zeros([2,2])
cond=tf.constant([  [True,False], [True,False]  ])
tf.where(cond,a,b)

'''
array([[1., 0.],
       [1., 0.]] )
'''


tf.where(cond) 
#这个就是查真的时候的地址  array([[0, 0],[1, 0]])    其中(0,0) ,(1,0)对应cond中的True的位置

#寻找一个非常大的张量里面的正数 或者负数
x=tf.random.normal([3,3])

'''
array([[ 0.6380522 , -1.4575384 , -1.452426  ],
       [ 0.15352641,  0.06791435, -0.7506055 ],
       [ 0.06677877, -1.3536417 ,  0.4606044 ]])

'''
mask=x>0

'''
array([[ True,  True,  True],
       [False, False, False],
       [False,  True, False]])
       相当于一个mask
'''
tf.where(mask)  #返回真值位置的坐标

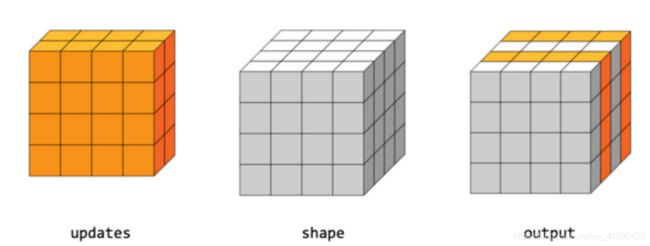
tf.scatter_nd(indices,updates,shape)

#可以批量刷新张量的固定地方值
#张量的indices,索引    update是要更新的数据

#用法是: 给定的一个指定shape的全0张量 , 分别将1,2,3,4插入到这个张量的第5,2,4,8的位置
indices=tf.constant([ [4],[1],[3],[7] ])  #分别在第5,2,4,8的位置
updates=tf.constant([ 1.,2.,3.,4. ]   )
shape =tf.constant([8])
tf.scatter_nd(indices,updates,shape) #结果为array([0., 2., 0., 3., 1., 0., 0., 4.] )

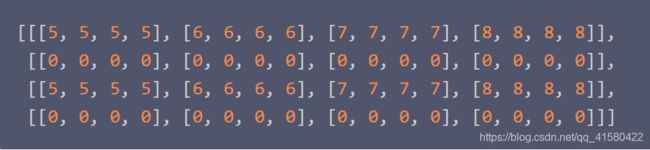
indices = tf.constant([[0], [2]])
updates = tf.constant([[[5, 5, 5, 5], [6, 6, 6, 6],
                        [7, 7, 7, 7], [8, 8, 8, 8]],
                       [[5, 5, 5, 5], [6, 6, 6, 6],
                        [7, 7, 7, 7], [8, 8, 8, 8]]])
shape = tf.constant([4, 4, 4])
scatter = tf.scatter_nd(indices, updates, shape)

tf.linspace( )

#在指定区间均分生成n个数
tf.linspace(0, 10, 5)  #在[0,10]中均分生成5个数，注意是闭合区间.

不同点
tf.range 使用的区间是左闭右开区间，tf.linspace使用的区间是闭合区间。
tf.range 使用delta参数来间接控制生成元素的个数，tf.linspace直接使用第三个参数num来控制生成元素的个数。

tf.meshgrid

#3d绘图
#tf.meshgrid    可以生成一个二维采样的坐标,方便对3d图的格式化

#例如 z=x^2 + y^2,画出来3d图
import numpy as np
from   mpl_toolkits.mplot3d   import  Axes3D
import  tensorflow   as tf

#第一种方式
points=[]
for  x in np.arange(-8 , 8 ,0.1):
    for y in np.arange(-8 , 8 ,0.1):
        z=x**2 + y**2
        points.append( [x,y,z] )

#第二种方式
x=tf.linspace(-8., 8.,  160)
y=tf.linspace(-8., 8.,  160)
x,y=tf.meshgrid(x,y)

z=x**2 + y**2

fig = plt.figure( )
ax = Axes3D(fig)
ax.contour3D(x,y,z,500)
plt.show()

1.5 数据集的加载和预处理

.

官方API网页

下载以后的地址在c下 如我的 C:\Users\weeks.keras\datasets

加载数据集

import  tensorflow   as tf

(x_train, y_train), (x_test, y_test)=tf.keras.datasets.mnist.load_data()

将数据集转换为tensor类型

#将数据集转为tensor类型的数据
train_db = tf.data.Dataset.from_tensor_slices (  (x_train,y_train) )
train_db =train_db.shuffle(10000) #随机的打散数据集

批训练

有时候数据集过大,不可能进行把全部的数据集都一次性拿进去的训练(机器可能吃不消啊),我们可以将数据集分成一批一批的训练.

#批训练   批训练的大小为batch_size
train_db =train_db.batch(8)    #显卡大算力强就增大 如128 意味着这一批训练128个样本

预处理

有时候我们下载的数据集并不一定满足我们输入的要求,于是对数据集进行预处理

#预处理,mnist的像素是0-255之间,我们进行预处理,使得输入在0-1之间
def  preprocess(x , y):
    x=tf.cast(x,dtype=tf.float32)/255
    y=tf.one_hot(y,depth=10)
    return   x,y


train_db=train_db.map(preprocess)
for   x, y in train_db:
    print(x,y)

#一个batch的训练    -->  1个step    60000/8   个step完成就是一次迭代 epoch  
#对于一个数据集来说,一般迭代多次epoch

#例如循环20次
for epoch in range(20):
    for step,(x,y) in enumerate(train_db):
        #训练

好博推荐一

好博推荐二

…

场景八:tf.Keras相关操作

最全Tensorflow2.0 入门教程持续更新

TensorFlow2.x学习笔记

keras是python语言开发的开源的神经网络的计算库。tf.keras
tensorflow中的keras是一套搭建和训练神经网络的一套高级API协议。
tf.kreas只能使用在tensorflow的后端中。但kreas本身是可以应用在多框架中。

#tf.keras
import  tensorflow   as tf
from    tensorflow import  keras
from    tensorflow.keras import  layers ,Sequential

#参考 官网 https://tensorflow.google.cn/api_docs/python/tf/keras?hl=en
x=tf.constant([1.,2.])
softmax= tf.keras.layers.Softmax( )
softmax(x)
#softmax用于多分类过程中，它将多个神经元的输出，映射到（0,1）区间内，可以看成概率来理解，从而来进行多分类！

1.1 神经网络定义

> >第一类神经网络定义写法

#tf.keras
import  tensorflow   as tf
from    tensorflow import  keras
from    tensorflow.keras import  layers ,Sequential

#定义神经网络
network= Sequential([
    layers.Dense(3),
    layers.ReLU(),
    layers.Dense(2,activation=layers.ReLU())   
     ]) 
#第一层三个神经元layers.Dense,    第一层用RELU激活函数   
#第二层两个神经元layers.Dense,    第二层用RELU激活函数    


x=tf.random.normal([4,3])
'''
x=
array([[ 1.3567505 ,  0.0463782 , -0.5099323 ],
       [-1.2894894 , -0.29622516, -0.54240394],
       [ 1.701698  , -0.2690858 , -0.06776197],
       [ 0.18689579, -0.6205667 , -1.1904672 ]], dtype=float32)
'''
network(x)  #可以查看经过神经网络处理的结果
#可以查看网络结构
network.summary()

参数12 第一层每一个神经元由w1x1+w2x2+w3x3+b构成，每一个神经元有4个参数(3个输入,一个b)
.
参数8 第二层神经元由w21x21 +w22x22 +w23x23 +b 构成，每一个神经元有4个参数。

>> 第二类神经网络定义写法–动态添加

动态的增加网络层数，先创建一个模型，向模型中添加

# 可选，第一层可以接收' input_shape '参数:

model = tf.keras.Sequential()
#第一层
model.add(tf.keras.layers.Dense(8, input_shape=(16,)))

#第二层
model.add(tf.keras.layers.Dense(4))

还可以这样

#先不指定输入的大小,build的时候指定
model = tf.kears.Sequential()    #实例化容器
model.add(layers.Dense(3))  #动态添加了一层3个神经元,构建全连接层
model.add(layers.Dense(2))

model.build((None, 2))    
#build的方法的作用是构建这个网络   None代表任意值,
#2代表有多少个特征跟第一层3个神经元做连接

len(model.weights)

model.summary()

1.2 模型训练

#模型的装配、训练与测试
#tf.keras
import  tensorflow   as tf
from    tensorflow import  keras
from    tensorflow.keras import  layers ,Sequential

#第一步定义神经网络
model= Sequential([
    layers.Dense(32,activation='relu'),  
    layers.Dense(16,activation='relu'),  
    layers.Dense(8,activation='relu'),  
    layers.Dense(10,activation='softmax')  #最后有10个分类
     ]) 

model.build(input_shape=(None,28*28))  #输入特征  下面的mnist数据集的大小为28*28
#model.summary()  可以查看参数


#第二步模型优化器
model.compile( optimizer= tf.keras.optimizers.SGD(learning_rate=0.001), 
               loss=tf.keras.losses.CategoricalCrossentropy(),
               metrics=['accuracy']
             )
'''
定义一个SGD的学习率为0.001的优化器 optimizer 
参考 https://tensorflow.google.cn/api_docs/python/tf/keras/optimizers/SGD?hl=en
定义损失函数loss
定义监控metrics  监控准确率
'''



#第三步 准备数据集
(x_train, y_train), (x_test, y_test)=tf.keras.datasets.mnist.load_data()  
train_db = tf.data.Dataset.from_tensor_slices (  (x_train,y_train) )
train_db =train_db.shuffle(10000) #随机的打散数据集
train_db =train_db.batch(8)    #批训练   批训练的大小为batch_size,显卡大算力强就增大 如128

#第四步 预处理
def  preprocess(x , y):
    x=tf.cast(x,dtype=tf.float32)/255.
    x=tf.reshape(x,  [-1,28*28])  #保持和上面输入的大小一样
    y=tf.one_hot(y,depth=10)
    return   x,y

train_db=train_db.map(preprocess)  #将数据应用到预处理中


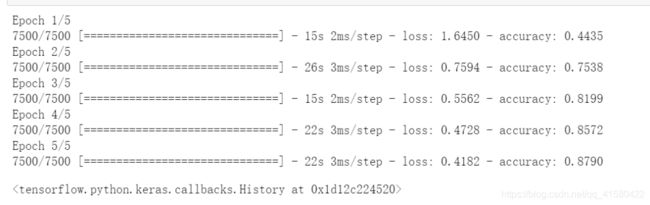
#训练
model.fit(train_db, epochs=5)    #epochs为迭代次数

#测试数据集
test_db = tf.data.Dataset.from_tensor_slices (  (x_test,y_test) )
test_db =test_db.shuffle(10000) #随机的打散数据集
test_db =test_db.batch(8)    #批训练   批训练的大小为batch_size,显卡大算力强就增大 如128
test_db=test_db.map(preprocess)

#预测
model.predict(test_db)

#查看结果
model.evaluate(test_db)   # [0.3157603144645691, 0.9129999876022339]

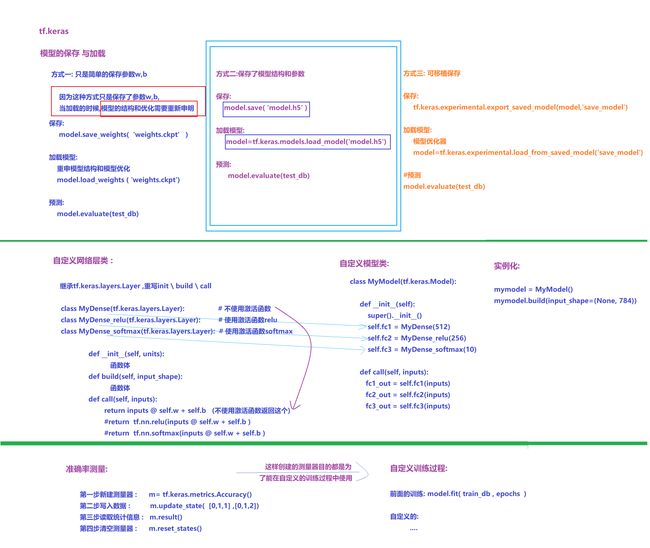
1.3 模型的保存和加载

>> 第一种方式 -->只保留参数w,b

#模型的保存与加载

#第一种方式,只保存w,b
''' 轻量级的模型保存 w,b   网络和优化器要和原来的一样    '''
model.save_weights( 'weights.ckpt' )


#如果有需要  删除model
#del model


#加载模型
#神经网络
model= Sequential([
    layers.Dense(32,activation='relu'),  
    layers.Dense(16,activation='relu'),  
    layers.Dense(8,activation='relu'),  
    layers.Dense(10,activation='softmax')  #最后有10个分类
     ]) 
#模型优化器
model.compile( optimizer= tf.keras.optimizers.SGD(learning_rate=0.001), 
               loss=tf.keras.losses.CategoricalCrossentropy(),
               metrics=['accuracy']
             )


#第三步加载
model.load_weights( 'weights.ckpt')

#预测
model.evaluate(test_db) #[0.31576013565063477, 0.9129999876022339]

> >第二种方式 -->保存了模型结构和参数

#第二种方式
#保存，保存了参数也保存了模型结构
model.save( 'model.h5' )

#读取
model=tf.keras.models.load_model('model.h5')

#预测
model.evaluate(test_db) #[0.31576013565063477, 0.9129999876022339]

> 第三种 -->可移植保存

#保存可移植模型,迁移到其他平台
tf.keras.experimental.export_saved_model(model,'save_model')

#读取,并不会读取出优化器
model2=tf.keras.experimental.load_from_saved_model('save_model')

#模型优化器
model.compile( optimizer= tf.keras.optimizers.SGD(learning_rate=0.001), 
               loss=tf.keras.losses.CategoricalCrossentropy(),
               metrics=['accuracy']
             )
#预测
model.evaluate(test_db) 

1.4 自定义网络层类

# 自定义网络层类
import tensorflow   as tf
from tensorflow import keras
from tensorflow.keras import layers, Sequential, datasets

#class MyDense(tf.keras.layers.Layer):  # 要继承tf.keras.layers.Layer类
#class MyDense_softmax(tf.keras.layers.Layer):  # 使用激活函数softmax

class MyDense_relu(tf.keras.layers.Layer):      # 使用激活函数relu
    # 第一步  自定义的全连接层
    def __init__(self, units):
        super().__init__()
        self.units = units

    def build(self, input_shape):
        self.w = self.add_variable(name='w',
                                   shape=[input_shape[-1], self.units],
                                   initializer=tf.initializers.RandomNormal())

        self.b = self.add_variable(name='w',
                                   shape=[self.units],
                                   initializer=tf.initializers.Zeros())

    def call(self, inputs):
    
        # Wi*Xj +b
        # W[input_shape[-1],units]
        # X [60000,784]
        
        return  tf.nn.relu(inputs @ self.w + self.b ) #使用激活函数relu
        #return  tf.nn.softmax(inputs @ self.w + self.b ) #使用激活函数softmax
        #return inputs @ self.w + self.b  #不使用激活函数

# 定义L1层,传入10个神经元
L1 = MyDense(10)

# 前项计算
x = tf.zeros([20, 15])
L1(x)

1.5 自定义模型类

使用激活函数在不同的问题上可能会带来不同的准确率的提升

import tensorflow   as tf
from tensorflow import keras
from tensorflow.keras import layers, Sequential, datasets


#第一步自定义网络层类 上面的Dense

#不使用激活函数的
class MyDense(tf.keras.layers.Layer):  # 要继承tf.keras.layers.Layer类
    def __init__(self, units):
        super().__init__()
        self.units = units
    def build(self, input_shape):
        self.w = self.add_variable(name='w',
                                   shape=[input_shape[-1], self.units],
                                   initializer=tf.initializers.RandomNormal())

        self.b = self.add_variable(name='w',
                                   shape=[self.units],
                                   initializer=tf.initializers.Zeros())

    def call(self, inputs):
        # Wi*Xj +b
        # W[input_shape[-1],units]
        # X [60000,784]
        return inputs @ self.w + self.b

#使用relu激活函数的
class MyDense_relu(tf.keras.layers.Layer):    
    def __init__(self, units):
        super().__init__()
        self.units = units

    def build(self, input_shape):
        self.w = self.add_variable(name='w',
                                   shape=[input_shape[-1], self.units],
                                   initializer=tf.initializers.RandomNormal())
        self.b = self.add_variable(name='w',
                                   shape=[self.units],
                                   initializer=tf.initializers.Zeros())
    def call(self, inputs):
         return  tf.nn.relu(inputs @ self.w + self.b ) #使用激活函数relu

#使用softmax激活函数的
class MyDense_softmax(tf.keras.layers.Layer):  
    def __init__(self, units):
        super().__init__()
        self.units = units
    def build(self, input_shape):
        self.w = self.add_variable(name='w',
                                   shape=[input_shape[-1], self.units],
                                   initializer=tf.initializers.RandomNormal())

        self.b = self.add_variable(name='w',
                                   shape=[self.units],
                                   initializer=tf.initializers.Zeros())
    def call(self, inputs):
        return  tf.nn.softmax(inputs @ self.w + self.b ) 

# 第二步自定义模型类
#不使用激活函数的
class MyModel(tf.keras.Model):
    def __init__(self):
        super().__init__()
        self.fc1 = MyDense(512)
        self.fc2 = MyDense(256)   #这是上面自己定义的MyDense
        self.fc3 = MyDense(128)
        self.fc4 = MyDense(10)

    def call(self, inputs):
        fc1_out = self.fc1(inputs)
        fc2_out = self.fc2(inputs)
        fc3_out = self.fc3(inputs)
        fc4_out = self.fc4(inputs)
        return fc4_out


#使用激活函数的
class MyModel2(tf.keras.Model):
    def __init__(self):
        super().__init__()
        self.fc1 = MyDense_relu(512) #这是上面自己定义的MyDense_relu
        self.fc2 = MyDense_relu(256)
        self.fc3 = MyDense_relu(128)
        self.fc4 = MyDense_softmax(10)

    def call(self, inputs):
        fc1_out = self.fc1(inputs)
        fc2_out = self.fc2(inputs)
        fc3_out = self.fc3(inputs)
        fc4_out = self.fc4(inputs)
        return fc4_out

# 实例化
mymodel = MyModel2()
mymodel.build(input_shape=(None, 784))  # 输入

mymodel.summary()

然后接入1.2的部分就可以进行自定义类的模型训练。

1.6 准确率测量/自定义训练过程

tensorflow2.x学习笔记二十四：tf.keras.metrics的使用

准确率测量

#测量 
#参考   https://tensorflow.google.cn/api_docs/python/tf/keras/metrics/Accuracy?hl=en
import  tensorflow  as tf
from    tensorflow import keras
from    tensorflow.keras import  layers ,Sequential, datasets

#准确率测量
#例如两个向量   真实值[0,1,1]   预测值[0,1,2]  准确率是2/3

#第一步新建测量器
m= tf.keras.metrics.Accuracy()

#第二步写入数据
m.update_state(  [0,1,1] ,[0,1,2])

#第三步读取统计信息
m.result()    #结果为

#第四步清空测量器
m.reset_states()

传入数据采用one_hot编码

import  tensorflow  as tf
from    tensorflow import keras
from    tensorflow.keras import  layers ,Sequential, datasets

#第一步新建测量器
m= tf.keras.metrics.CategoricalAccuracy()

#第二步写入数据
m.update_state(   [ [0,0,1] ,[0,1,0] ] , [ [0.1,0.9,0.8],[0.05,0.95,0] ]   )  #前面的参数采取了one_hot编码

#第三步读取统计信息
m.result()     #

#第四步清空测量器
m.reset_states()
#还有其他数据传入方式 参考 https://tensorflow.google.cn/api_docs/python/tf/keras/metrics?hl=en

> 自编测量器和训练过程

# 创建自己的测量器
import tensorflow  as tf
from tensorflow import keras
from tensorflow.keras import layers, Sequential, datasets
import datatime   #可取消

# 新建测量器
acc_meter = tf.keras.metrics.Accuracy()
loss_meter = tf.keras.metrics.Mean()

# 第一步定义神经网络
model = Sequential([
    layers.Dense(32, activation='relu'),
    layers.Dense(16, activation='relu'),
    layers.Dense(8, activation='relu'),
    layers.Dense(10, activation='softmax')  # 最后有10个分类
])

model.build(input_shape=(None, 28 * 28))  # 输入特征  下面的mnist数据集的大小为28*28

# 第二步模型优化器
model.compile(optimizer=tf.keras.optimizers.SGD(learning_rate=0.001),
              loss=tf.keras.losses.CategoricalCrossentropy(),
              metrics=['accuracy']
              )


# 第三步 预处理
def preprocess(x, y):
    x = tf.cast(x, dtype=tf.float32) / 255.
    x = tf.reshape(x, [-1, 28 * 28])  # 保持和上面输入的大小一样
    y = tf.one_hot(y, depth=10)
    return x, y


# 第四步 准备训练数据集
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
train_db = tf.data.Dataset.from_tensor_slices((x_train, y_train))
train_db = train_db.shuffle(10000)  # 随机的打散数据集
train_db = train_db.batch(8)  # 批训练   批训练的大小为batch_size,显卡大算力强就增大 如128
train_db = train_db.map(preprocess)

# 准备测试数据集
test_db = tf.data.Dataset.from_tensor_slices((x_test, y_test))
test_db = test_db.shuffle(10000)  # 随机的打散数据集
test_db = test_db.batch(8)  # 批训练   批训练的大小为batch_size,显卡大算力强就增大 如128
test_db = test_db.map(preprocess)

# 训练
# model.fit(train_db, epochs=5)    #epochs为迭代次数

# 自定义训过程
op = tf.keras.optimizers.Adam(0.01)

current_time = datetime.datetime.now().strftime("%Y%m%d-%H%M%S")  # 打印当前时间
log_dir = 'logs/' + current_time  #可取消  和上面的行
summary_writer = tf.summary.create_file_writer(log_dir)

for epoch in range(2):
    for step, (x, y) in enumerate(train_db):
        with   tf.GradientTape()  as  tape:
            loss = tf.losses.categorical_crossentropy(y, model(x))

            # 测量器写入数据
            loss_meter.update_state(loss)
        grads = tape.gradient(loss, model.trainable_variables)
        op.apply_gradients(zip(grads, model.trainable_variables))

        if step % 100 == 0:
            print('epoch:', epoch, 'step:', step, 'loss:', loss_meter.result().numpy())

            with summary_writer.as_default():  #可取消掉时间
                tf.summary.scalar(name='loss', data=loss_meter.result().numpy())

            # 清空测量器
            loss_meter.reset_states()

    for step, (x, y) in enumerate(test_db):
        out = model(x)
        pred = tf.cast(tf.argmax(out, axis=-1), dtype=tf.int32)
        y = tf.cast(tf.argmax(y, axis=-1), dtype=tf.int32)
        acc_meter.update_state(y, pred)
    print('epoch:', epoch, 'acc:', acc_meter.result().numpy())

    with summary_writer.as_default():  #可取消掉  
        tf.summary.scalar(name='acc', data=loss_meter.result().numpy(), step=epoch)
    acc_meter.reset_states()

# 预测
# model.predict(test_db)

还是不厌其烦的推荐下面两个比较细致的博客

最全Tensorflow2.0 入门教程持续更新

TensorFlow2.x学习笔记

…

场景九:卷积神经网络

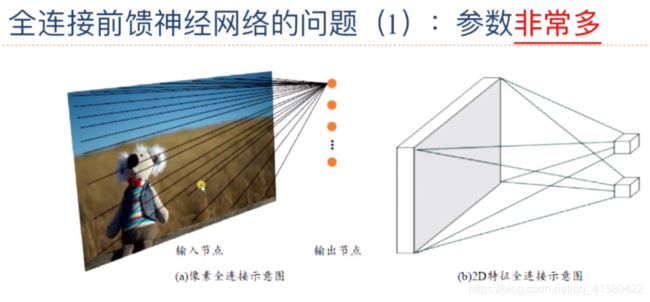
1.1 问题引入

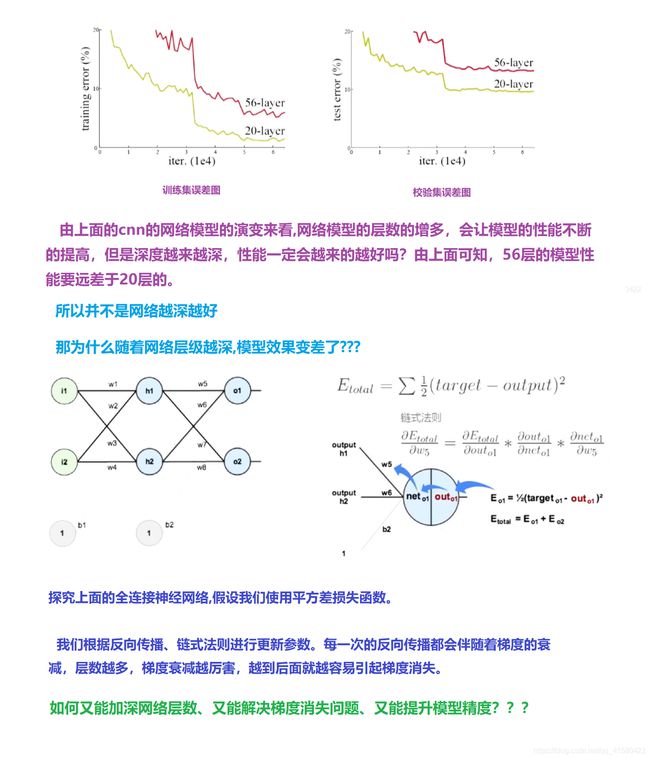
全连接神经网络受到机器的好坏的严重影响，这会占用很大的计算资源。 会受显卡显存的制约。矩阵参数比较多，计算量大。

参数过多，应该考虑是否将所有的特征都输入到全神经网络的模型中，我们应该考虑一些比较重要的特征，如上面的考拉的特征，而降低对草地这种特征的参考价值，这将会大大的降低参数过多问题。

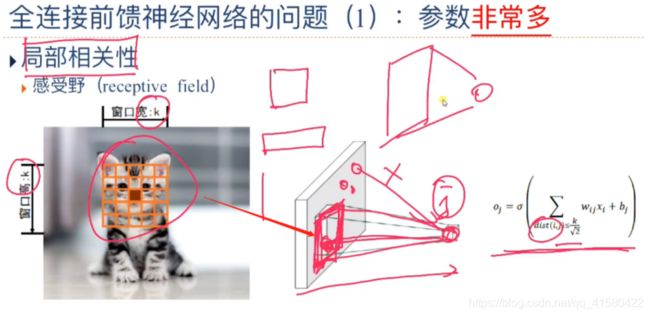
如上图的神经网络中的一个元素计算，只考虑了左边KxK正方形区域的像素点，这将有效的降低参数的个数，实现局部相关性。

1.2 卷积

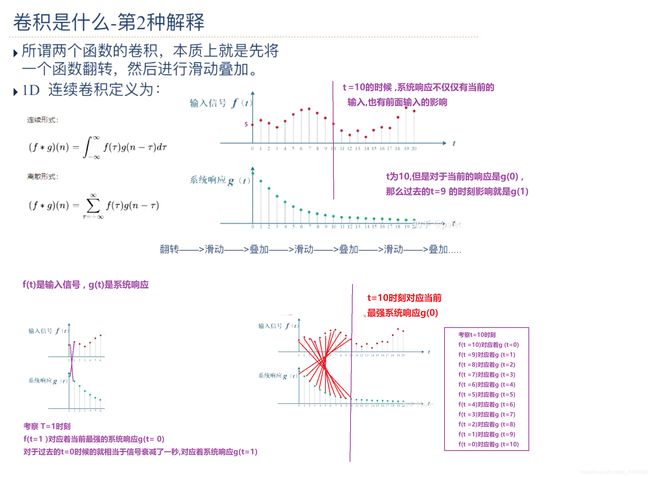
参考博文

由上图可知:输入信号f(t) 在前面时间对系统响应g(t1)影响较小。后面对g(t)影响较大。

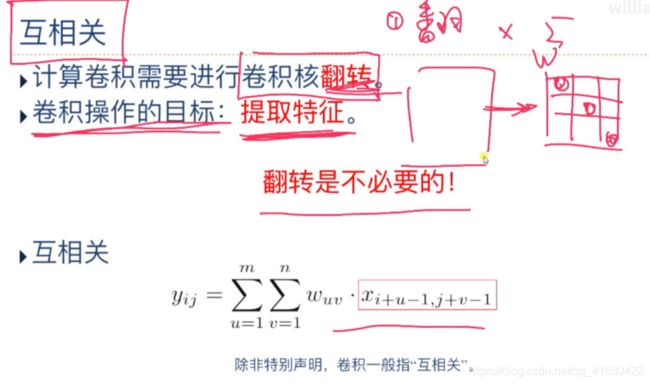
卷积操作: 先翻转再平移,然后求和
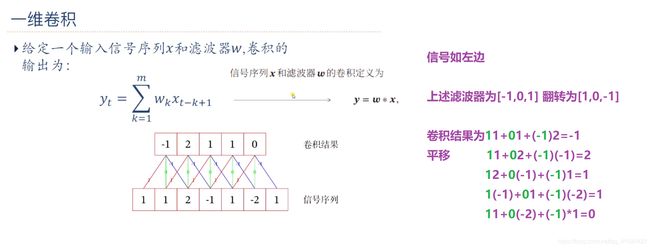
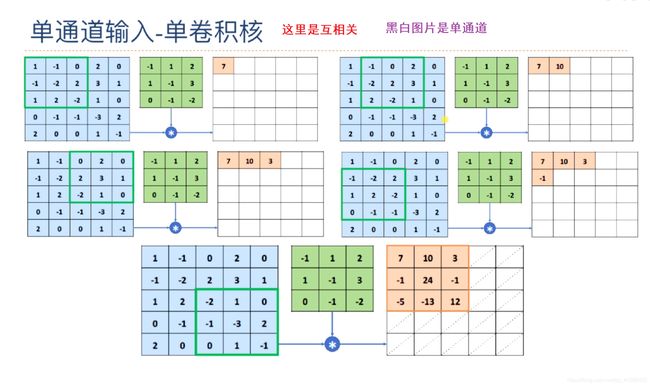
在深度学习中，如果不特别声明，卷积操作不是原始味道的卷积，它是一个互相关操作，但是我们还是通称为卷积

一维卷积

二维卷积

互相关代替卷积操作

w的矩阵是可以事先定义的或者处理的，原始概念的卷积是先翻转w的，但是我们可以对w事先处理，变为互相关操作，即不需要再进行翻转操作。
.
在深度学习中，如果不特别声明，卷积操作不是原始味道的卷积，它是一个互相关操作，但是我们还是通称为卷积。

卷积拓展

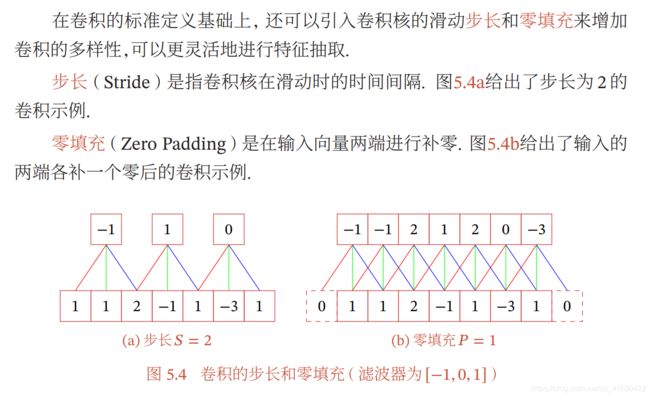
对于mxm 图片 , 卷积核大小为nxn,在指定步长s的时候,或者有填充p 一定要确保(m-n+2p)/s的值是整数,得到的特征图片的大小为(m-n+2p)/s +1
.
例如上面的5x5像素图, 卷积核是3x3,不填充,步长为1. 特征图大小为(5-3 +2*0) /1 +1=3 -->(3,3)
.
如果左右填充一个0,得到的特征图大小为(5-3+2)/1 +1 =5 -->(5,5)

.

如果左右填充一个0,步长为3,得到的特征图大小为(5-3+2)/3 +1不为整数,通常调节步长或者重新指定卷积核的大小.

黑白图片的卷积

彩色图片的卷积

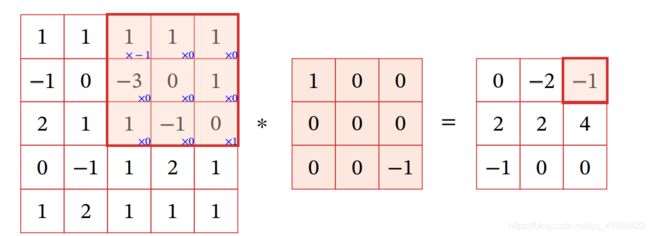
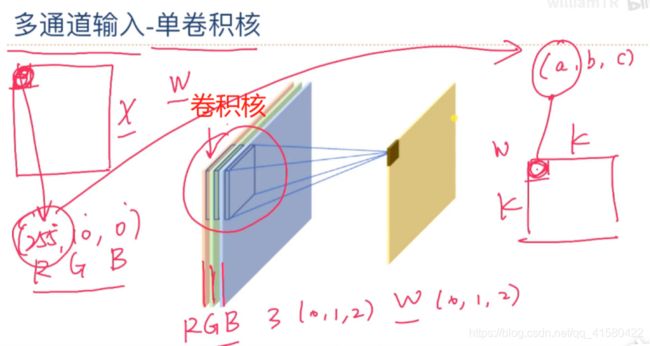
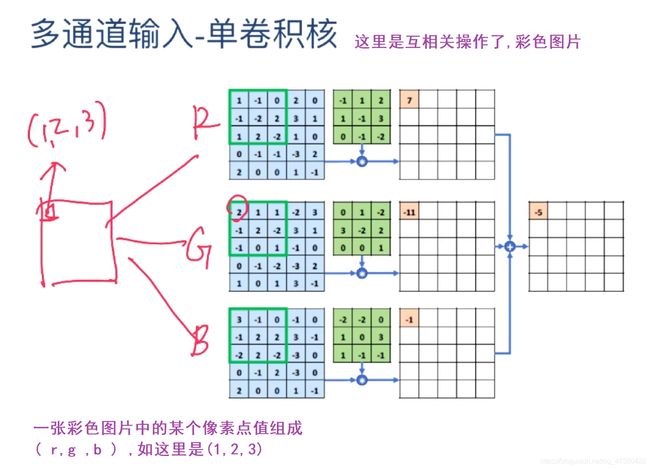
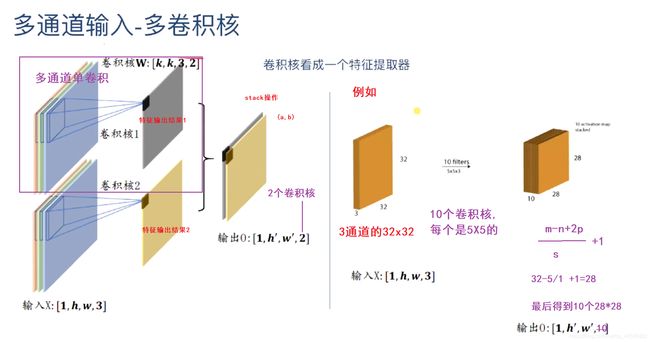
卷积核的数量要和通道数量一致。卷积核就是w矩阵。

tensorflow中卷积实现

>>方式一: tf.nn.conv2d()

#卷积操作
import  tensorflow as tf
from  tensorflow  import  keras

x=tf.random.normal([1,5,5,3]) # input是输入  [batch, in_height, in_width, in_channels]
w=tf.random.normal([3,3,3,6])   # [filter_height, filter_width, in_channels, out_channels] 这边的通道数3一定要和上面的一致

out1=tf.nn.conv2d(input=x,   filters=w,   strides=[1,1,1,1],
                  padding=[[0, 0], [0, 0],[0, 0], [0, 0]],
                  data_format='NHWC', dilations=None,name=None )

>>方式二: tf.keras.layers.Conv2D()

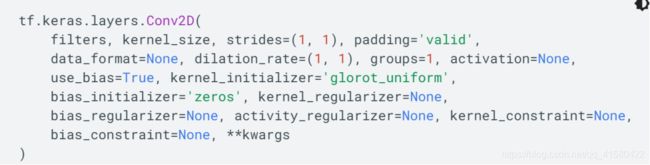
除了上面的方法,还可以Con2D 这个卷积层类,不过是tf.keras.layers中的方法,不再有input.

# 这种方法不用额外定义卷积核
'''
cnnlayer=  tf.keras.layers.Conv2D(
                          filters=4, kernel_size=3, strides=(1, 1), padding='valid',
                          data_format=None, dilation_rate=(1, 1), groups=1, activation=None,
                          use_bias=True, kernel_initializer='glorot_uniform',
                          bias_initializer='zeros', kernel_regularizer=None,
                          bias_regularizer=None, activity_regularizer=None, kernel_constraint=None,
                          bias_constraint=None)
'''

# 卷积操作
import tensorflow as tf
from tensorflow import keras

x = tf.random.normal([1, 5, 5, 3])
cnnlayer = tf.keras.layers.Conv2D(filters=5, kernel_size=3)
# 没有指定的参数就为默认  filters=4就是卷积核的个数 kernel_size就是2就是卷积核的大小

cnnlayer.trainable_variables  # 这个可以看到w和b的值 [3,3,3,5]   第一个3是输入有3个通道  3x3是大小,最后一个5是输出的通道数
out2 = cnnlayer(x)  # x的形状是[1,5,5,3] ,out2是[1,3,3,5]

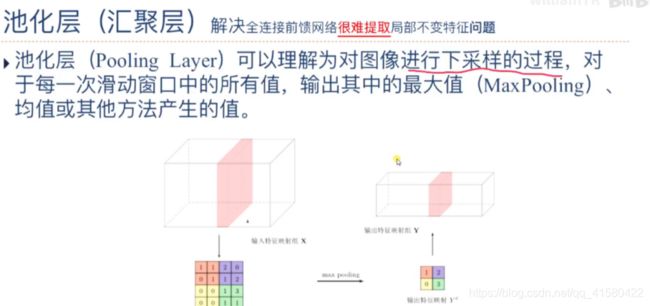
1.3 池化 -->汇聚层/子采样层

池化大大降低了特征空间,也可以减少过拟合,同时也能增加下一次的感受野。

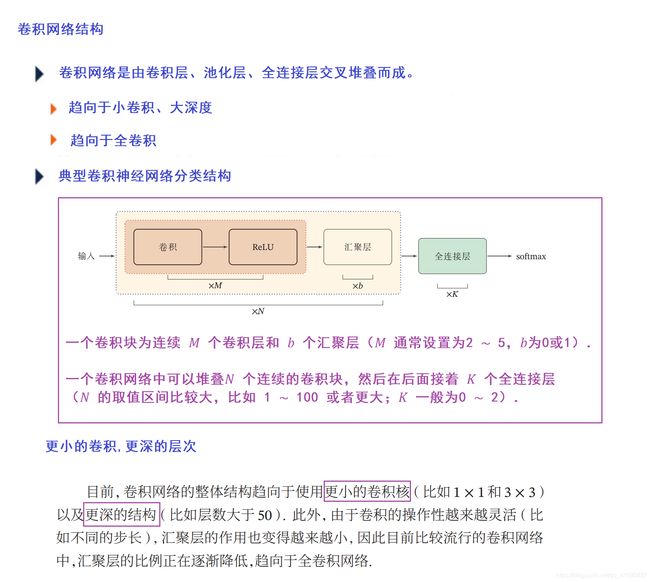
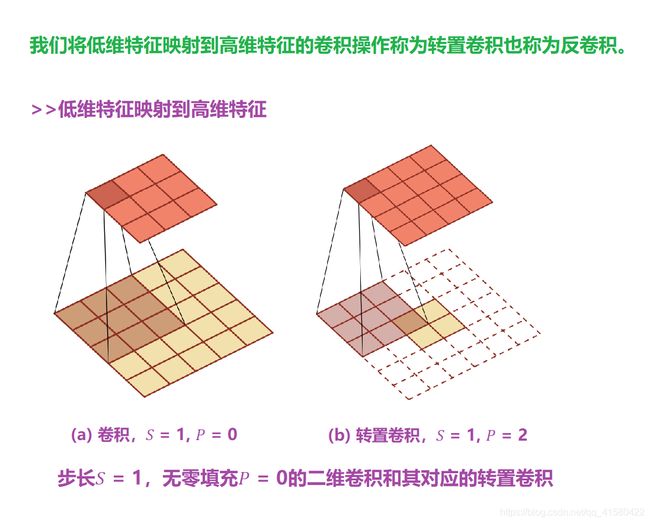
1.4 卷积神经网络结构与反卷积神经网络

例如下面的LeNet-5

特征可视化查看每一层学到什么

详细原理----->使用反卷积（Deconvnet）可视化ＣＮＮ卷积层，查看各层学到的内容

>>表示学习

表示学习（特征学习）

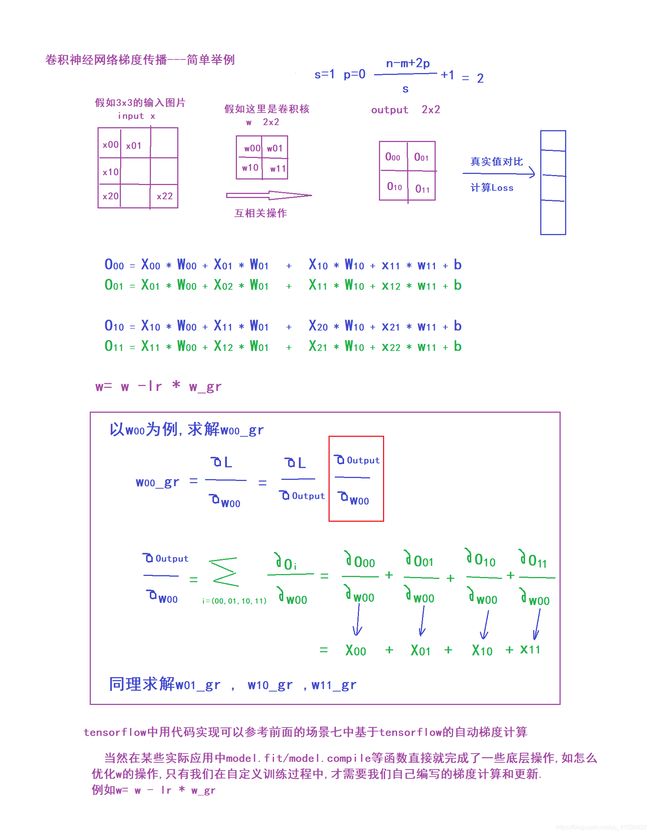
1.5 卷积涉及的梯度计算

理论部分(可跳过)

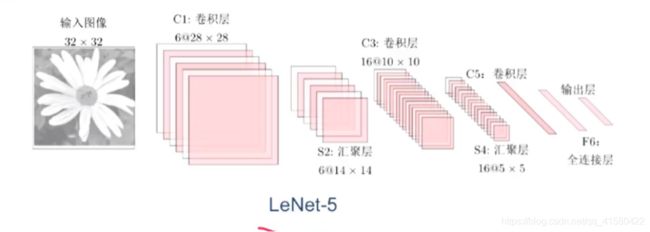
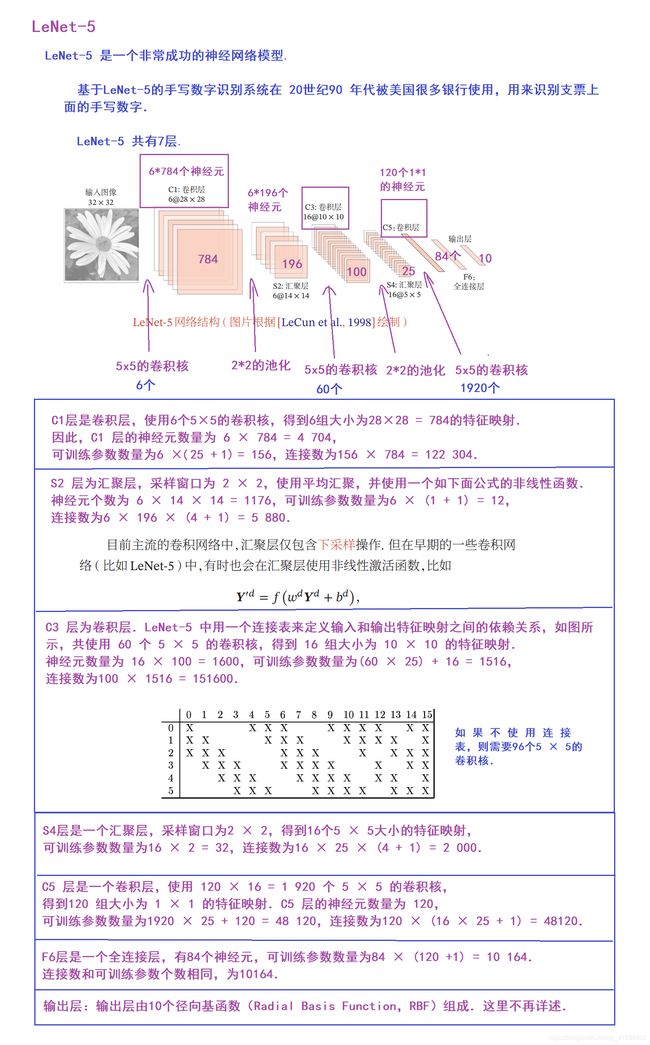
1.6 LeNet-5 (1998年 7层左右)

# LeNet-5的实现
import tensorflow  as tf
from tensorflow import keras

batch = 32
model = tf.keras.Sequential([
    keras.layers.Conv2D(6, 5),
    # 卷积核的个数6, 卷积核的大小是5X5  原来输入32x32 卷积输出为6X28X28
    keras.layers.MaxPooling2D(pool_size=2, strides=2),  # 池化  strides 相当于步长 池化后大小为6x14x14
    keras.layers.ReLU(),  # 激活函数

    keras.layers.Conv2D(16, 5),
    # 卷积核的个数16, 卷积核的大小是5X5 原来输入6x14x14  卷积输出为16X10X10
    keras.layers.MaxPooling2D(pool_size=2, strides=2),  # 池化  池化后大小为16x5x5
    keras.layers.ReLU(),  # 激活函数    

    keras.layers.Flatten(),  # 拉平操作
    keras.layers.Dense(120, activation='relu'),
    keras.layers.Dense(84, activation='relu'),
    keras.layers.Dense(10, activation='softmax')
])

model.build(input_shape=(batch, 28, 28, 1))
# model.summary()

# 优化器
model.compile(optimizer=keras.optimizers.Adam(),
              loss=keras.losses.CategoricalCrossentropy(),
              metrics=['accuracy']
              )
# 预处理
def preprocess(x, y):
    x = tf.cast(x, dtype=tf.float32) / 255.
    x = tf.reshape(x, [-1, 28, 28, 1])  # 保持和上面输入的大小一样
    y = tf.one_hot(y, depth=10)
    return x, y


# 准备训练数据集
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
train_db = tf.data.Dataset.from_tensor_slices((x_train, y_train))
train_db = train_db.shuffle(10000)  # 随机的打散数据集
train_db = train_db.batch(8)  # 批训练   批训练的大小为batch_size,显卡大算力强就增大 如128
train_db = train_db.map(preprocess)

# 准备测试数据集
test_db = tf.data.Dataset.from_tensor_slices((x_test, y_test))
test_db = test_db.shuffle(10000)  # 随机的打散数据集
test_db = test_db.batch(8)  # 批训练   批训练的大小为batch_size,显卡大算力强就增大 如128
test_db = test_db.map(preprocess)

# 训练
model.fit(train_db, epochs=5)  # epochs为迭代次数

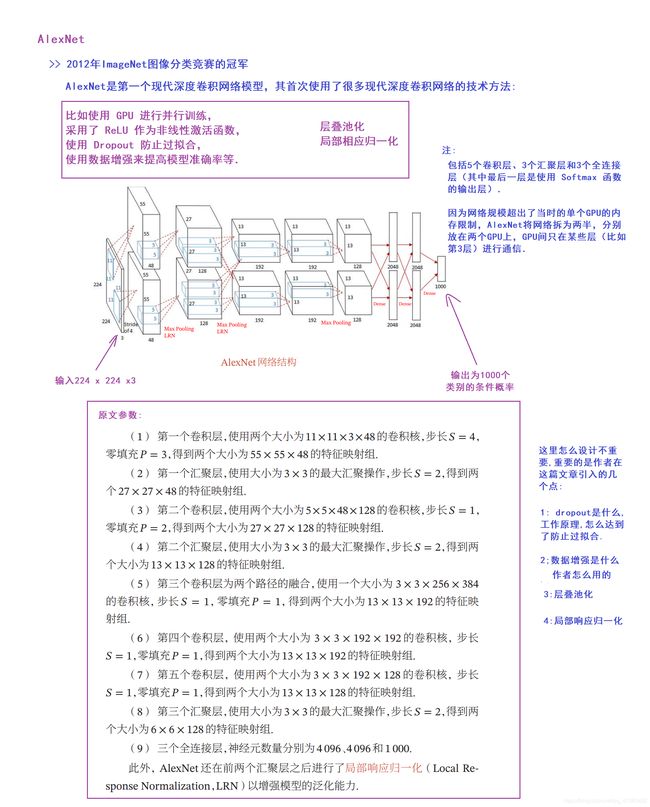
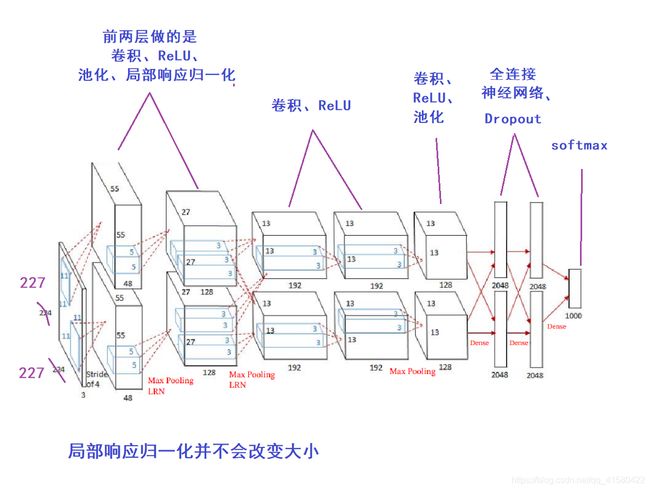
1.7 AlexNet (2012年 8层左右)

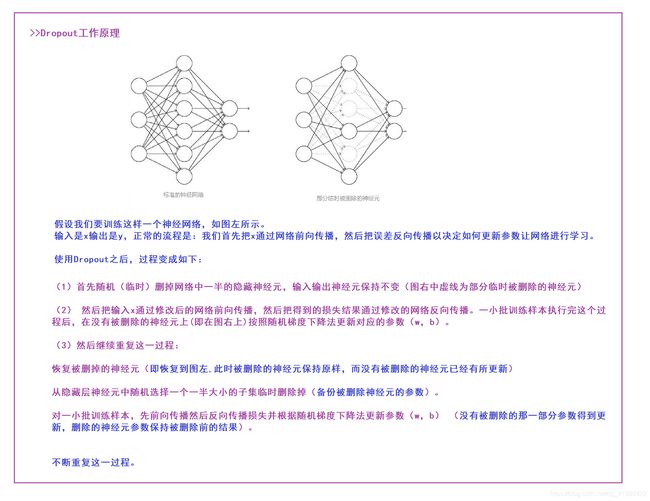
① Dropout

深度学习中Dropout原理解析

② 数据增强

数据增强及实现

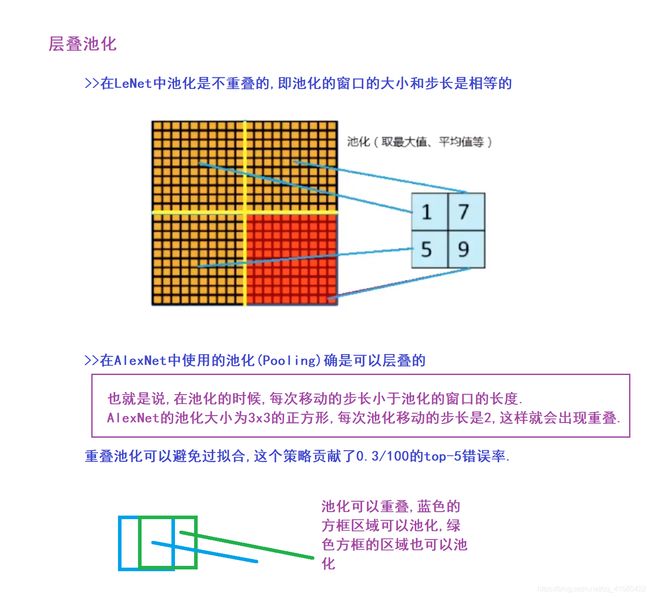
③ 层叠池化

④ 局部响应归一化

局部响应归一化现在已经被BN/GN替代

实现

# AlexNet的实现,有点区别在于,lenet-5一层管一件事情,这个一层可能干了好几件事情
import tensorflow  as tf
from tensorflow import keras

'''
#第一层网络的定义
x=tf.random.normal( [1,227,227,3] )

#卷积
c1_c = tf.keras.layers.Conv2D(96,11,4)    #通道数是48+48  卷积核的大小为11  步长为4
out1= c1_c(x)     #卷积结果为relu-->池化-->局部响应归一化
    keras.layers.Conv2D(96, 11, 4),
    keras.layers.ReLU(),
    keras.layers.MaxPooling2D((3, 3), 2),
    keras.layers.BatchNormalization(),  # 这里使用了bn代替了上面的LRN    shape=(1, 27, 27, 96)

    # 第二层
    c2(),
    keras.layers.ReLU(),
    keras.layers.MaxPooling2D((3, 3), 2),
    keras.layers.BatchNormalization(),  # 这里使用了bn代替了上面的LRN    

    # 第三层
    keras.layers.Conv2D(384, 3, 1, padding='same'),
    keras.layers.ReLU(),

    # 第四层
    keras.layers.Conv2D(384, 3, 1, padding='same'),
    keras.layers.ReLU(),

    # 第五层
    keras.layers.Conv2D(256, 3, 1, padding='same'),
    keras.layers.ReLU(),
    keras.layers.MaxPooling2D((3, 3), 2),

    # 拉平,全连接层
    keras.layers.Flatten(),
    keras.layers.Dense(4096),
    keras.layers.ReLU(),
    keras.layers.Dropout(0.25),

    keras.layers.Dense(1000),
    keras.layers.Softmax()
])

alexnet.build(input_shape=[None, 227, 227, 3])
alexnet.summary()

# 优化器
# 预处理
# 准备训练数据集 数据集的尺寸大小要大于227x227
# 准备测试数据集
# 训练

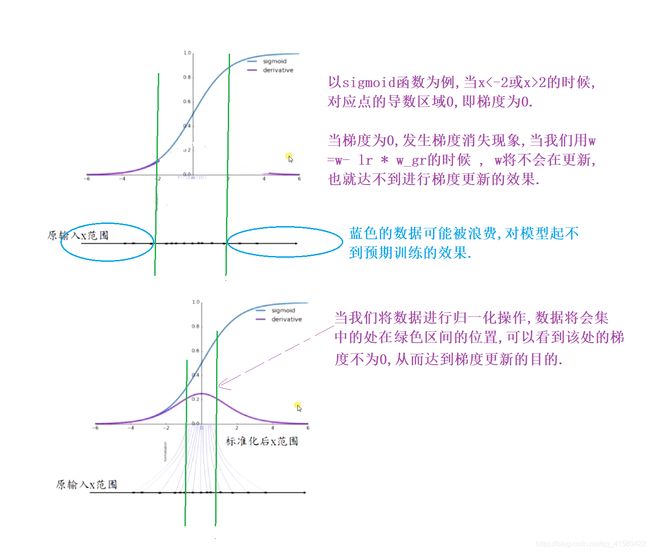
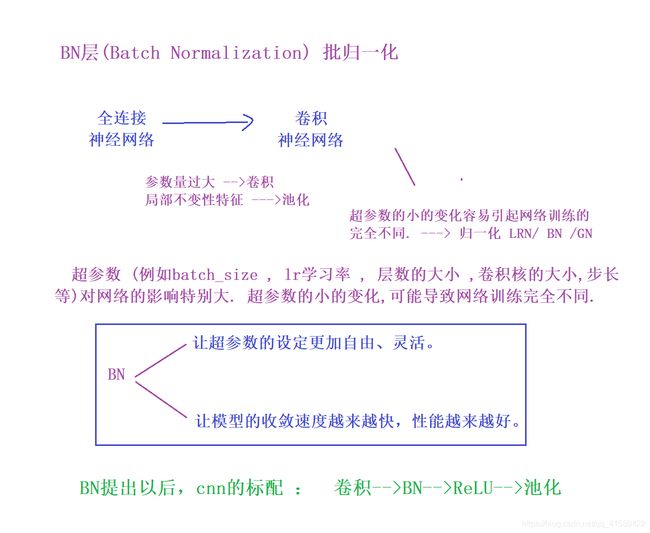
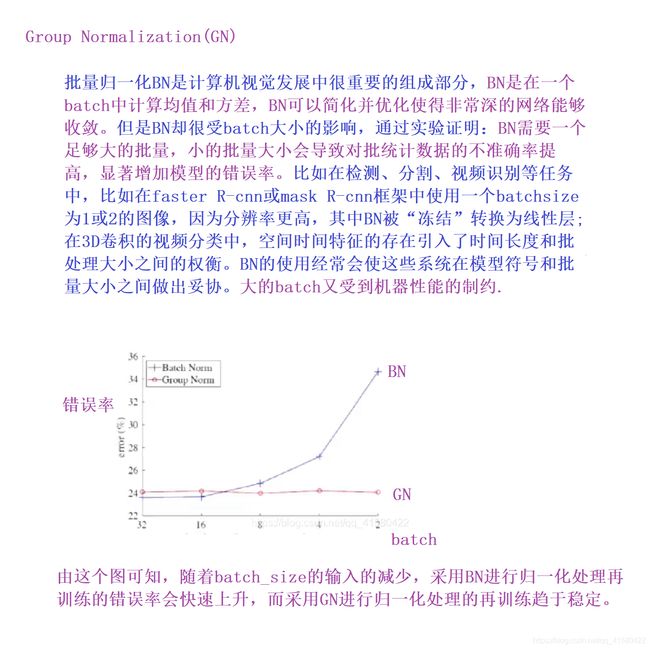
1.8 归一化 BN层 /GN层

BN

深度学习之9——逐层归一化(BN，LN)

GN层

深度学习之17——归一化(BN+LN+IN+GN)

深度学习归一化：BN、GN与FRN

简单应用

#BN的应用
import  tensorflow as  tf
from    tensorflow  import  keras

#[b.h.w.c]
x=tf.random.normal([100,32,32,3])

x=tf.reshape(x , [-1,3] )
tf.reduce_mean( x,axis = 0 )


model= tf.keras.Sequential([ 
    keras.layers.Conv2D(6,3),
    keras.layers.BatchNormalization(), #BN归一化
    keras.layers.ReLU(),
    keras.layers.MaxPool2D()
])

out =model(x,training=True)   #训练的时候,用traing=True/False控制BN在测试还是训练上使用
model.variables

当然还可以不使用上面的BatchNormalization(),自定义归一化处理

.

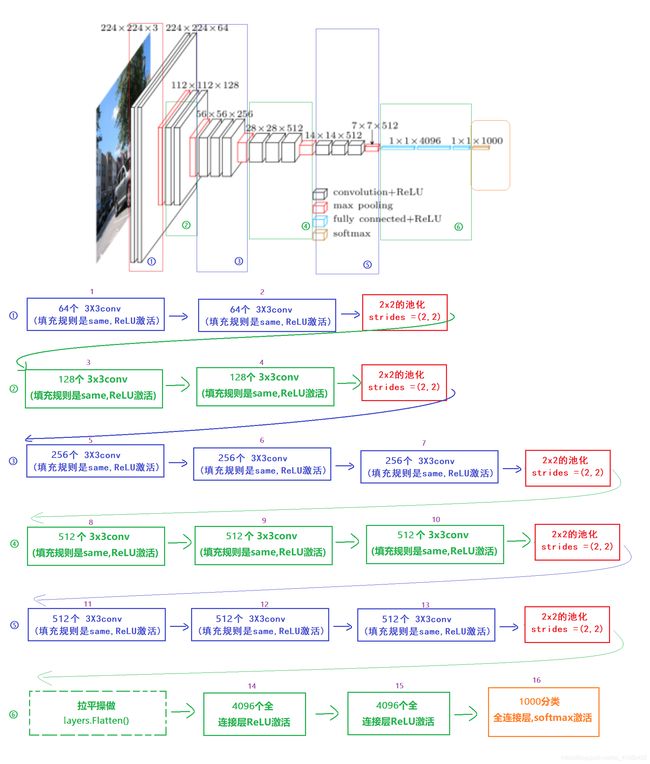
1.9 VGG网络 (2014年第二名 13,16,19层左右)*

# vgg实现
import tensorflow as  tf
from tensorflow import keras
from tensorflow.keras import datasets, layers, optimizers, models, regularizers
import numpy as np

# 网络模型
# vgg16模型   cifar10  是10个分类,    imagenet是1000个分类

num_class = 10
model = models.Sequential()

model.add(layers.Conv2D(64, (3, 3), padding='same', activation='relu'))
model.add(layers.Conv2D(64, (3, 3), padding='same', activation='relu'))
model.add(layers.MaxPooling2D((2, 2), strides=(2, 2)))

model.add(layers.Conv2D(128, (3, 3), padding='same', activation='relu'))
model.add(layers.Conv2D(128, (3, 3), padding='same', activation='relu'))
model.add(layers.MaxPooling2D((2, 2), strides=(2, 2)))

model.add(layers.Conv2D(256, (3, 3), padding='same', activation='relu'))
model.add(layers.Conv2D(256, (3, 3), padding='same', activation='relu'))
model.add(layers.Conv2D(256, (3, 3), padding='same', activation='relu'))
model.add(layers.MaxPooling2D((2, 2), strides=(2, 2)))

model.add(layers.Conv2D(512, (3, 3), padding='same', activation='relu'))
model.add(layers.Conv2D(512, (3, 3), padding='same', activation='relu'))
model.add(layers.Conv2D(512, (3, 3), padding='same', activation='relu'))
model.add(layers.MaxPooling2D((2, 2), strides=(2, 2)))

model.add(layers.Conv2D(512, (3, 3), padding='same', activation='relu'))
model.add(layers.Conv2D(512, (3, 3), padding='same', activation='relu'))
model.add(layers.Conv2D(512, (3, 3), padding='same', activation='relu'))
model.add(layers.MaxPooling2D((2, 2), strides=(2, 2)))

model.add(layers.Flatten())
model.add(layers.Dense(4096, activation='relu'))
model.add(layers.Dense(4096, activation='relu'))
model.add(layers.Dense(1000, activation='softmax'))

model.build(input_shape=(None, 32, 32, 3))
# model.summary()

# 模型优化器
model.compile(optimizer=keras.optimizers.Adam(0.0001),
              loss=keras.losses.CategoricalCrossentropy(from_logits=True),
              metrics=['accuracy']
              )

> 进一步处理

# 零 均值 归一化
def normalize(x_train, x_test):
    x_train = x_train / 255.
    x_test = x_test / 255.

    # 求训练集的均值与方差
    mean = np.mean(x_train, axis=(0, 1, 2, 3))
    std = np.std(x_train, axis=(0, 1, 2, 3))  # 方差
    print('mean:', mean, 'std:', std)

    x_train = (x_train - mean) / (std + 1e-7)
    x_test = (x_test - mean) / (std + 1e-7)
    return x_train, x_test

# 读取数据
(x_train, y_train), (x_test, y_test) = datasets.cifar10.load_data()
(x_train.shape, y_train.shape), (x_test.shape, y_test.shape)

# 归一化处理
x_train, x_test = normalize(x_train, x_test)

def preprocess(x, y):
    x = tf.cast(x, tf.float32)
    y = tf.cast(y, tf.int32)
    y = tf.squeeze(y, axis=1)
    y = tf.one_hot(y, depth=10)
    return x, y

# 准备训练数据集
train_db = tf.data.Dataset.from_tensor_slices((x_train, y_train))
train_db = train_db.shuffle(50000)
train_db = train_db.batch(8)
train_db = train_db.map(preprocess)

# 准备测试数据集
test_db = tf.data.Dataset.from_tensor_slices((x_test, y_test))
test_db = test_db.shuffle(10000)  # 随机的打散数据集
test_db = test_db.batch(8)  # 批训练   批训练的大小为batch_size,显卡大算力强就增大 如128
test_db = test_db.map(preprocess)

# 训练
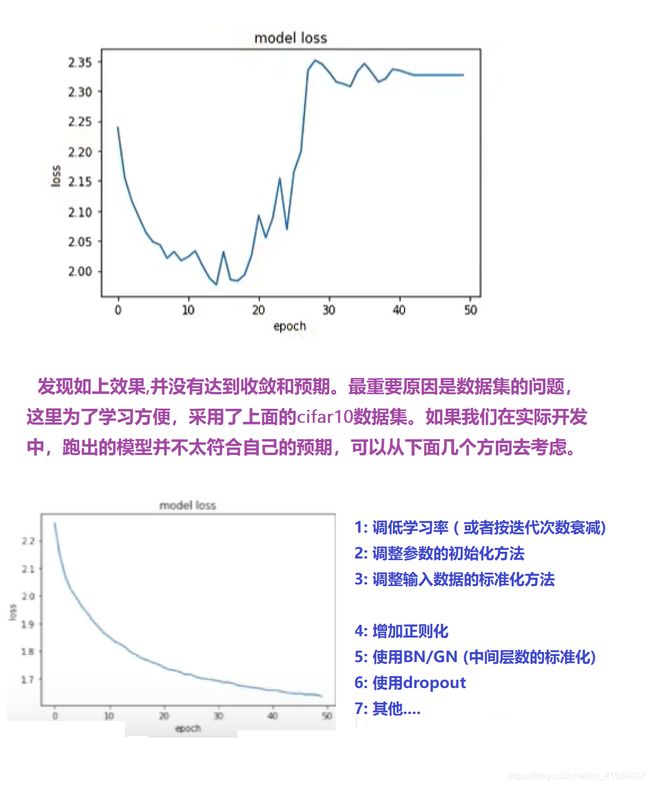
history = model.fit(train_db, epochs=2)  # epochs为迭代次数

import matplotlib.pyplot  as  plt
plt.plot(history.history['loss'])
plt.title("model  loss")
plt.ylabel("loss")
plt.xlabel("epoch")
plt.show()

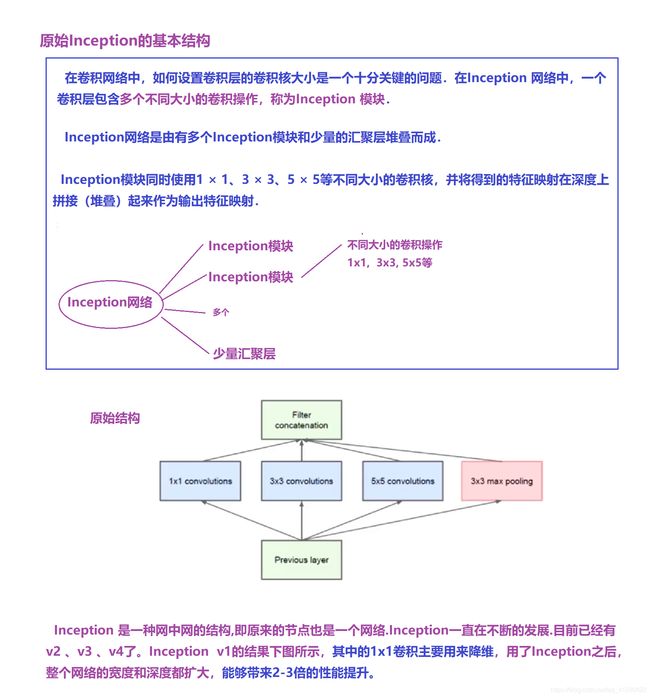
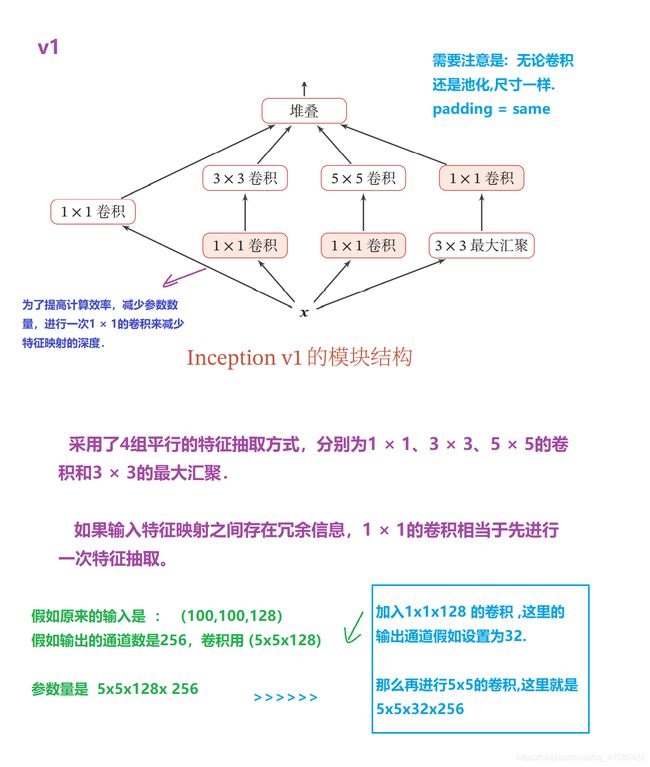
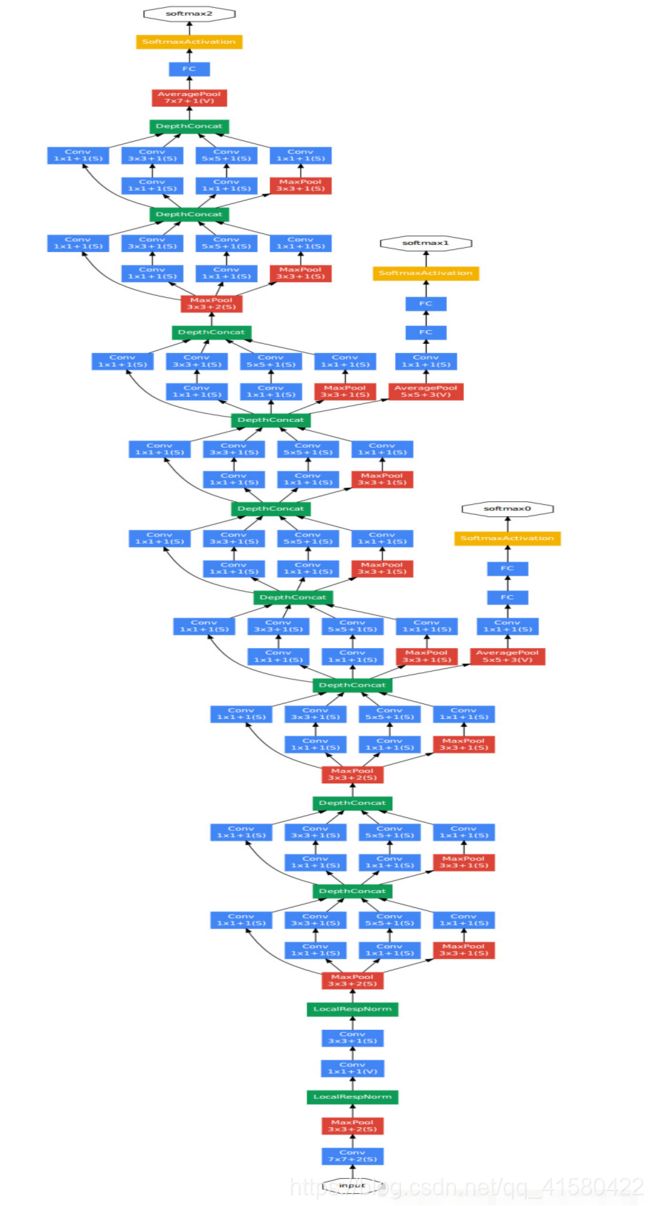
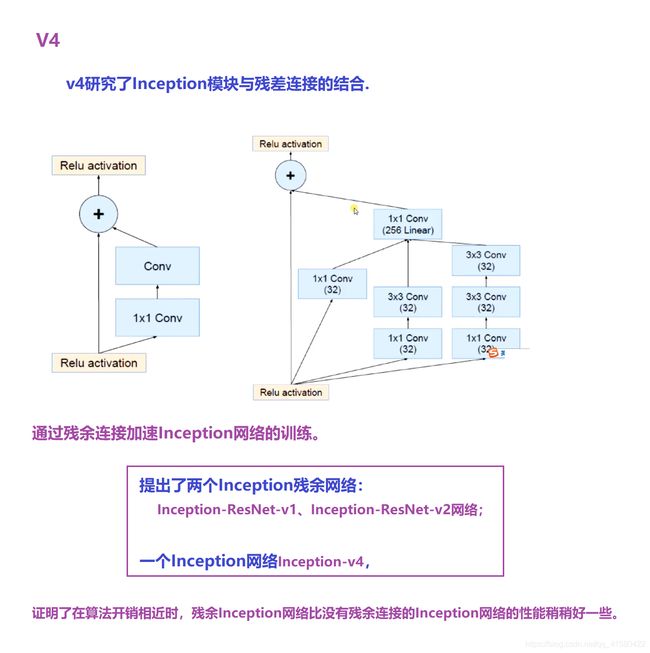
1.10 Inception网络

Inception V1,V2,V3,V4 模型总结

① Inception —>GoogLeNet网络 (2014年第一名 22层)

下面清晰图可见

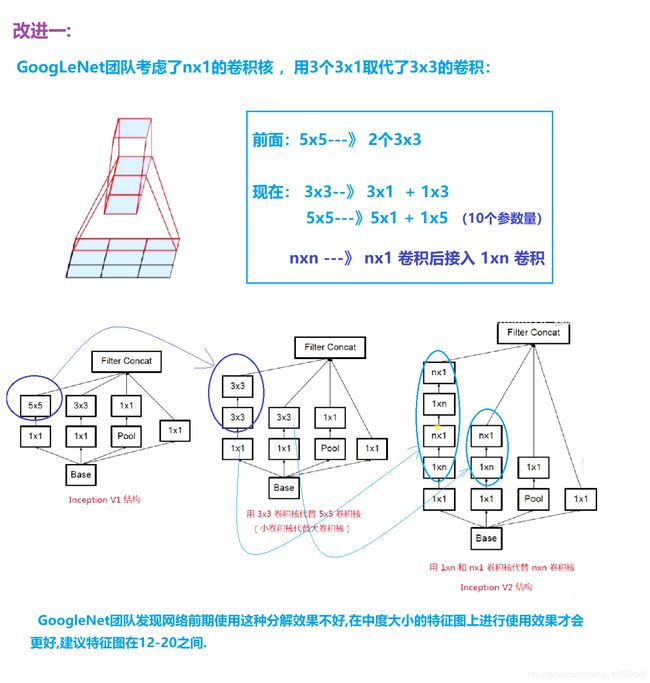
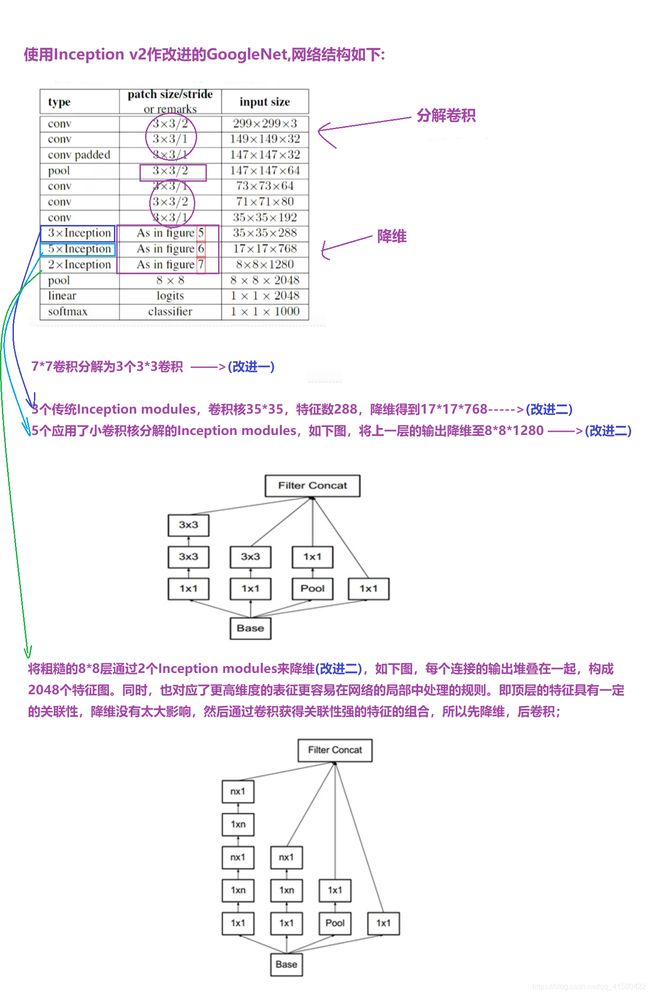
② Inception v2

③ Inception v3

④ Inception v4

应用

# GoogLeNet实现  基于Inception v2
import os
import tensorflow as  tf
import numpy    as np
from tensorflow import keras


# 定义一个卷积类
class ConvBNRelu(keras.Model):

    # 扩展基本卷积层Conv+BN+ReLU   BN层的一个作用就是让我们的学习率不仔那么的重要
    def __init__(self, filters, kernelsize=3, strides=1, padding='same'):
        super().__init__()

        self.model = keras.models.Sequential([
            keras.layers.Conv2D(filters=filters,
                                kernel_size=kernelsize,
                                strides=strides,
                                padding=padding),
            keras.layers.BatchNormalization(),
            keras.layers.ReLU()
        ])

    # 前向传播
    def call(self, x, training=None):
        x = self.model(x, training=training)
        return x


class Inception_v2(keras.Model):

    # 构造Inception v2模块
    def __init__(self, filters, strides=1):
        # strides  控制是否缩减特征图  -1 不缩减   -2 缩减

        super().__init__()

        # 卷积
        self.conv1_1 = ConvBNRelu(filters, kernelsize=1, strides=1)
        self.conv1_2 = ConvBNRelu(filters, kernelsize=3, strides=1)
        self.conv1_3 = ConvBNRelu(filters, kernelsize=3, strides=strides)

        self.conv2_1 = ConvBNRelu(filters, kernelsize=1, strides=1)
        self.conv2_2 = ConvBNRelu(filters, kernelsize=3, strides=strides)

        self.pool = keras.layers.MaxPooling2D(pool_size=3, strides=strides, padding='same')

    # 前向传播
    def call(self, x, training=None):
        x1_1 = self.conv1_1(x, training=training)
        x1_2 = self.conv1_2(x1_1, training=training)
        x1_3 = self.conv1_3(x1_2, training=training)

        x2_1 = self.conv2_1(x, training=training)
        x2_2 = self.conv2_2(x2_1, training=training)

        x3 = self.pool(x)

        # 在最后一个,即通道维度上
        x = tf.concat([x1_3, x2_2, x3], axis=3)
        return x


class GoogLeNet(keras.Model):

    def __init__(self, num_blocks, num_classes, filters=16):
        '''
        构造GoogLeNet模型
        num_blocks :包含具有相同filters的n个Inception_v2模块的block数量
        num_classes :分类数量
        filters: 卷积核的个数

        '''
        super().__init__()
        self.filters = filters
        self.conv1 = ConvBNRelu(filters)  # 第一个卷积层

        self.blocks = keras.models.Sequential()  # 购置动态数量的Inception_v2组合模块

        for block_id in range(num_blocks):
            for Inception_id in range(2):
                if Inception_id == 0:
                    block = Inception_v2(self.filters, strides=2)  # 第一个Inception缩放
                else:
                    block = Inception_v2(self.filters, strides=1)  # 其他Inception不缩放
                self.blocks.add(block)

            # 下一层的block中的卷积数量比上一层的卷积数量多一倍
            self.filters *= 2

        self.avg_pool = keras.layers.GlobalAveragePooling2D()
        self.fc = keras.layers.Dense(num_classes, activation='softmax')

    def call(self, x, training=None):
        out = self.conv1(x, training=training)
        out = self.blocks(out, training=training)
        out = self.avg_pool(out)
        out = self.fc(out)
        return out

model = GoogLeNet(2, 10)
model.build(input_shape=(None, 32, 32, 3))
model.summary()

# 模型优化器
model.compile(optimizer=keras.optimizers.Adam(0.0001),
              loss=keras.losses.CategoricalCrossentropy(from_logits=True),
              metrics=['accuracy']
              )

> 进一步处理

# 零 均值 归一化
def normalize(x_train, x_test):
    x_train = x_train / 255.
    x_test = x_test / 255.

    # 求训练集的均值与方差
    mean = np.mean(x_train, axis=(0, 1, 2, 3))
    std = np.std(x_train, axis=(0, 1, 2, 3))  # 方差
    print('mean:', mean, 'std:', std)

    x_train = (x_train - mean) / (std + 1e-7)
    x_test = (x_test - mean) / (std + 1e-7)
    return x_train, x_test


# 读取数据
(x_train, y_train), (x_test, y_test) = datasets.cifar10.load_data()

# 归一化处理
x_train, x_test = normalize(x_train, x_test)


def preprocess(x, y):
    x = tf.cast(x, tf.float32)
    y = tf.cast(y, tf.int32)
    y = tf.squeeze(y, axis=1)
    y = tf.one_hot(y, depth=10)
    return x, y


# 准备训练数据集
train_db = tf.data.Dataset.from_tensor_slices((x_train, y_train))
train_db = train_db.shuffle(50000)
train_db = train_db.batch(8)
train_db = train_db.map(preprocess)

# 准备测试数据集
test_db = tf.data.Dataset.from_tensor_slices((x_test, y_test))
test_db = test_db.shuffle(10000)  # 随机的打散数据集
test_db = test_db.batch(8)  # 批训练   批训练的大小为batch_size,显卡大算力强就增大 如128
test_db = test_db.map(preprocess)

# 训练
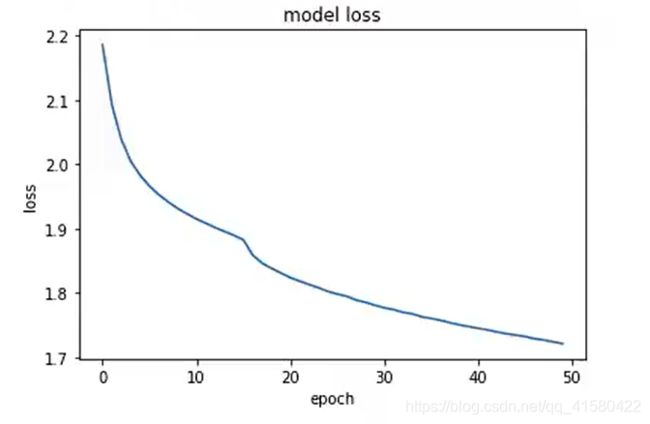
history = model.fit(train_db, epochs=2)  # epochs为迭代次数

> 迭代次数可以放大,展示效果.

import  matplotlib.pyplot  as  plt

plt.plot(history.history['loss'])
plt.title("model  loss")
plt.ylabel("loss")
plt.xlabel("epoch")
plt.show()

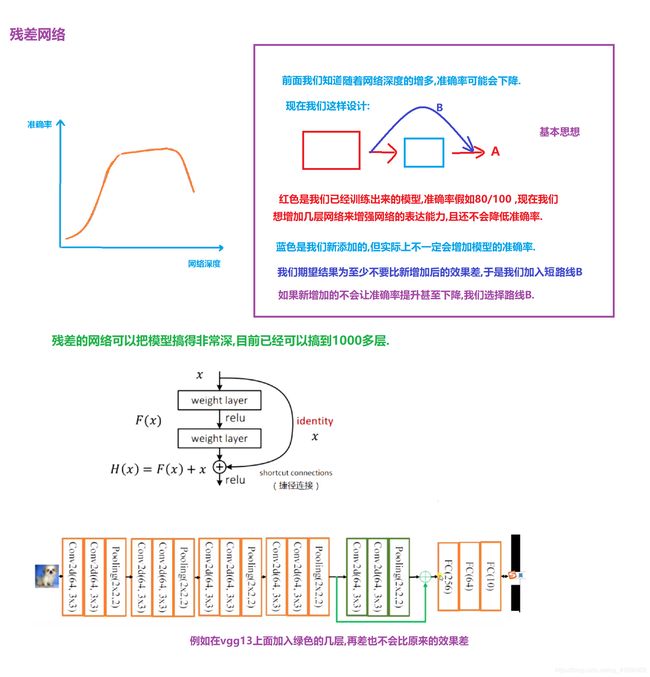
1.11 ResNet（2015第一名）

2015年ImageNet ILSVRC冠军论文学习 - ResNet

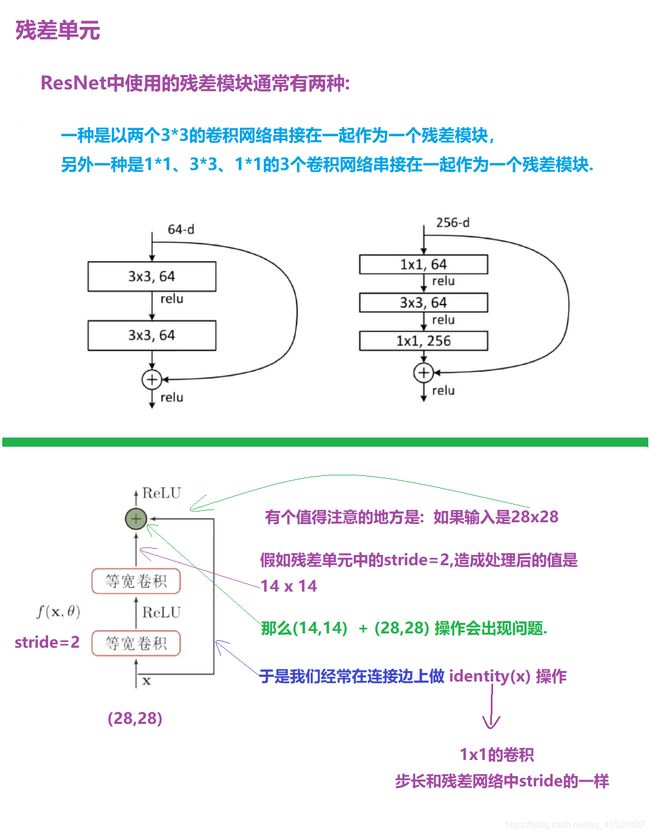
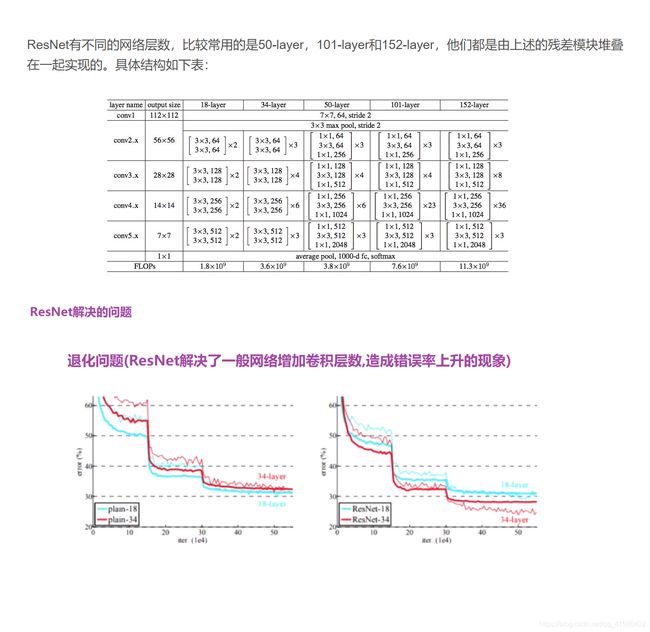
# ResNet实现
import os
import tensorflow as  tf
import numpy    as np
from tensorflow import keras

num_classes = 10
batch_size = 32
epochs = 10


class ResnetBlock(keras.Model):

    def __init__(self, filters, kernelsize=3, strides=1, padding='same'):
        super().__init__()

        self.conv_model = keras.models.Sequential([

            # 第一个卷积层
            keras.layers.Conv2D(filters=filters,
                                kernel_size=kernelsize,
                                strides=strides,
                                padding=padding),
            keras.layers.BatchNormalization(),
            keras.layers.ReLU(),

            # 第二个卷积层
            keras.layers.Conv2D(filters=filters,
                                kernel_size=kernelsize,
                                strides=1,
                                padding=padding),
            keras.layers.BatchNormalization()
        ])

        if strides != 1:
            # 即F(x)和x的大小不同时,需要创建identity(x)卷积层
            self.identity = keras.models.Sequential([
                keras.layers.Conv2D(filters=filters,
                                    kernel_size=1,
                                    strides=strides,
                                    padding=padding)
            ])
        else:
            # 保持原样输出
            self.identity = lambda x: x

    def call(self, inputs, training=None):
        conv_out = self.conv_model(inputs)
        identity_out = self.identity(inputs)
        out = conv_out + identity_out
        out = tf.nn.relu(out)
        return out


class ResNet(keras.Model):
    def __init__(self, block_list, num_classes):
        # block_list :block中的卷积核个数与block的数量,eg.[[64,3],[128,4],[256,6]]

        super().__init__()

        self.conv_initial = tf.keras.layers.Conv2D(16, 5, 1, padding='same')
        self.blocks = keras.models.Sequential()

        for block_id in range(len(block_list)):
            for layer_id in range(block_list[block_id][1]):
                if layer_id == 0:
                    # 每块中的第一个conv 的stride=2
                    self.blocks.add(ResnetBlock(filters=block_list[block_id][0], strides=2))
                else:
                    # 其他conv的stride为1
                    self.blocks.add(ResnetBlock(filters=block_list[block_id][0], strides=1))

        self.final_bn = keras.layers.BatchNormalization()
        self.avg_pool = keras.layers.GlobalAveragePooling2D()
        self.fc = keras.layers.Dense(num_classes)

    def call(self, inputs, training=None):
        out = self.conv_initial(inputs)
        out = self.blocks(out, training=training)
        out = self.final_bn(out, training=training)
        out = tf.nn.relu(out)
        out = self.avg_pool(out)
        out = self.fc(out)

        return out


model = ResNet([[64, 2], [128, 3], [256, 4]], num_classes)
model.build(input_shape=(None, 32, 32, 3))
model.summary()

# 模型优化器
model.compile(optimizer=keras.optimizers.Adam(0.001),
              loss=keras.losses.CategoricalCrossentropy(from_logits=True),
              metrics=['accuracy']
              )
#其他操作          

1.12 其他卷积种类、总结

>>转置卷积/反卷积

参考前面1.4 卷积神经网络结构与反卷积神经网络

转置卷积(Transpose Convolution)

微步卷积

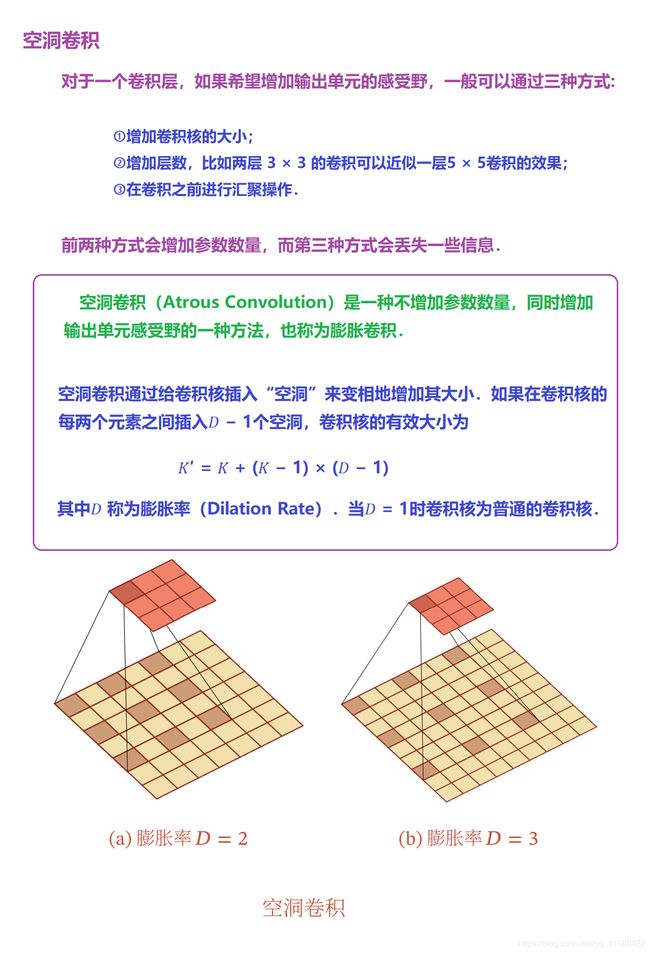
>>空洞卷积

空洞卷积

> 总结


> 应用：

…

场景十:rcnn /faster rcnn

.

you did it

…

<深度解读指环王>