PyTorch中文手册学习记录（2）第二、三章

P y T o r c h 中 文 手 册 阅 读 ＆ 复 现

2019-10-17

第二章 pytorch基础汇总

注意：本章内容与第一章有大量重复。

第一节 torch包和torchvision包

1. 张量

• .item()：取出数值（0维＆1维单元素）
• torch.ones_like(x)：创建x大小的张量
• long=tensor.long()：变类型
• numpy_a = a.numpy()：转numpy（共享底层）
• torch_a = torch.from_numpy(numpy_a)：转torch（共享底层）
• gpu_a=cpu_a.cuda()：转gpu
• gpu_b=cpu_b.to(device)：转device指定gpu（device = torch.device("cuda")）
• max_value, max_idx = torch.max(x, dim=1)：沿行取最大值
• sum_x = torch.sum(x, dim=1)：每行求和
• x.add_(y)：加（与x=x+y底层操作不同）

2. 自动求导

多元素需指定gradient参数：

x = torch.rand(3, 3, requires_grad=True)
y = torch.rand(3, 3, requires_grad=True)
z= x**2+y**3
z.backward(torch.ones_like(x))
print(x.grad)

>>>
tensor([[0.2087, 1.3554, 0.5560],
        [1.2655, 0.1223, 0.8008],
        [1.1052, 0.2579, 1.8006],)

autograd过程：
1.执行z.backward()时，这个操作将调用z里面的grad_fn这个属性，执行求导的操作。
2.这个操作将遍历grad_fn的next_functions，然后分别取出里面的Function（AccumulateGrad），执行求导操作。这部分是一个递归的过程直到最后类型为叶子节点。
3.计算出结果以后，将结果保存到他们对应的variable 这个变量所引用的对象（x和y）的 grad这个属性里面。
4.求导结束。所有的叶节点的grad变量都得到了相应的更新。

3. nn包和优化器optm

• PyTorch准备好了现成的网络模型，只要继承nn.Module，并实现它的forward方法，PyTorch会根据autograd，自动实现backward函数，在forward函数中可使用任何tensor支持的函数，还可以使用if、for循环、print、log等Python语法，写法和标准的Python写法一致。（即：网络模型中实现forward不是为了调用而是为了自动生成backward）

注意:torch.nn只支持mini-batches，不支持一次只输入一个样本，即一次必须是一个batch。所有的输入都会增加一个维度，4维input最前面的1即为batch-size。

• nn管前向传播，所以loss函数直接在nn里。而optimizer在torch.optim中

4. 数据加载＆预处理

Dataset是一个抽象类, 为了能够方便的读取，需要将要使用的数据包装为Dataset类。 自定义的Dataset需要继承它并且实现两个成员方法：
1.__getitem__() 该方法定义用索引(0 到 len(self))获取一条数据或一个样本
2.__len__() 该方法返回数据集的总长度

class Bull(Dataset):
    def __init__(self,csv_file):
        self.df=pd.read_csv(csv_file)
    def __len__(self):
        return len(self.df)
    def __getitem__(self, idx):
        return self.df.iloc[idx].SalePrice

ds_demo=Bull('median_benchmark.csv')

DataLoader为我们提供了对Dataset的读取操作，返回可迭代对象：

dl=torch.utils.data.DataLoader(ds_demo,batch_size=10,
                               shuffle=True,num_workers=0)

torchvision.datasets数据包：

import torchvision.datasets as datasets
trainset=datasets.MNIST(root='./data',train=True,download=True,transform=None)

torchvision.models模型包：

import torchvision.models as models
resnet18=models.resnet18(pretrained=True)

torchvision.transforms图像处理包：

from torchvision import transforms as transforms
transform = transforms.Compose([
    transforms.RandomCrop(32, padding=4),  #先四周填充0，在把图像随机裁剪成32*32
    transforms.RandomHorizontalFlip(),  #图像一半的概率翻转，一半的概率不翻转
    transforms.RandomRotation((-45,45)), #随机旋转
    transforms.ToTensor(),
    transforms.Normalize((0.4914, 0.4822, 0.4465), (0.229, 0.224, 0.225)), 
    #R,G,B每层的归一化用到的均值和方差  # Mnist数据集的归一化参数
])

第二节 简单的例程

线性回归：

import torch
from torch.nn import Linear,MSELoss,Module
from torch.optim import SGD
import numpy as np
import pandas as pd
import matplotlib
import matplotlib.pyplot as plt
import seaborn as sns
x=np.linspace(0,20,500)
x=np.random.rand(256)
noise=np.random.randn(256)/4
y=x*5+7+noise
df=pd.DataFrame()
df['x']=x
df['y']=y
sns.lmplot(x='x',y='y',data=df)
plt.show()
model=Linear(1,1)
criterion=MSELoss()
optim=SGD(model.parameters(),lr=0.01)
epochs=3000
x_train=x.reshape(-1,1).astype('float32')  ###
y_train=y.reshape(-1,1).astype('float32')  ###
for i in range(epochs):
    inputs=torch.from_numpy(x_train)
    labels=torch.from_numpy(y_train)
    outputs=model(inputs)
    optim.zero_grad()
    loss=criterion(outputs,labels)
    loss.backward()
    optim.step()
    if(i%100==0):
        print('epoch {},loss{:1.4f}'.format(i,loss.data.item()))
[w,b]=model.parameters()
print(w.item(),b.item())

1998 LeNet5网络：

import torch.nn as nn
import torch.nn.functional as F
class LeNet5(nn.Module):
    def __init__(self):
        super(LeNet5,self).__init__()
        self.conv1=nn.Conv2d(1,6,5)
        self.conv2=nn.Conv2d(6,16,5)
        self.fc1=nn.Linear(16*5*5,120)
        self.fc2=nn.Linear(120,84)
        self.fc3=nn.Linear(84,10)
    def forward(self, x):
        x=F.max_pool2d(F.relu(self.conv1(x)),2)
        x=F.max_pool2d(F.relu(self.conv2(x)),2)
        x=x.view(-1,x.num_flat_features(x))
        x=F.relu(self.fc1(x))
        x=F.relu(self.fc2(x))
        x=self.fc3(x)
        return x
    def num_flat_features(self,x):
        size=x.size()[1:]
        num_features=1
        for s in size:
            num_features*=s
        return num_features
net=LeNet5
print(net)

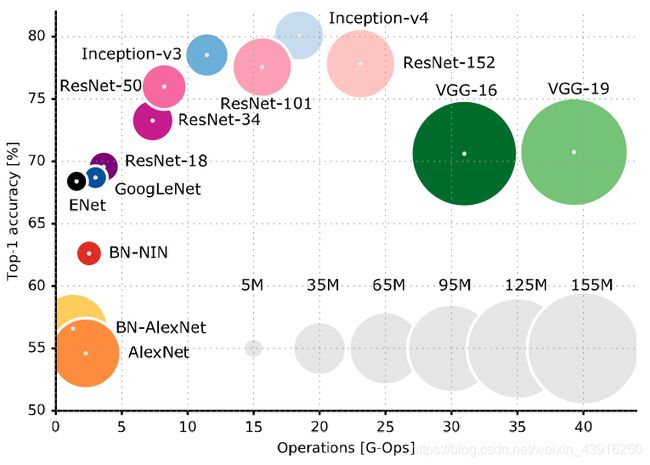
2012 AlexNet：
添加LRN（局部响应标准化）层，目前已被dropout等取代。

2014 GoogleNet：
1×1的核减少特征数

2015 VGG：
小卷积核代替大卷积核

2015 ResNet：
跳连接

主流卷积网络大小：

RNN：

import torch.nn as nn
import torch
rnn=nn.RNN(20,50,2)
input=torch.randn(100,32,20)
h_0=torch.randn(2,32,50)
output,hu=rnn(input,h_0)
print(output.size(),hu.size())

第三章

第一节 logistic回归

logistic回归: 线性回归后经由某一逻辑函数进行回归

import torch.nn as nn
import torch
import numpy as np
data =np.loadtxt('german.data-numeric')
n,l=data.shape
for j in range(l-1):
    meanVal=np.mean(data[:,j])
    stdVal=np.std(data[:,j])
    data[:,j]=(data[:,j]-meanVal)/stdVal
np.random.shuffle(data)
train_data=data[:900,:l-1]
train_lab=data[:900,l-1]-1
test_data=data[900:,:l-1]
test_lab=data[900:,l-1]-1

class LR(nn.Module):
    def __init__(self):
        super(LR,self).__init__()
        self.fc1=nn.Linear(24,2)
    def forward(self, x):
        x=self.fc1(x)
        x=torch.sigmoid(x)
        print(x)
def test(pred,lab):
    t=pred.max(-1)[1]==lab
    return torch.mean(t.float())

net=LR()
criterion=nn.CrossEntropyLoss() # 使用CrossEntropyLoss损失
optm=torch.optim.Adam(net.parameters()) # Adam优化
epochs=1000 # 训练1000次

for i in range(epochs):
    # 指定模型为训练模式，计算梯度
    net.train()
    # 输入值都需要转化成torch的Tensor
    x=torch.from_numpy(train_data).float()
    y=torch.from_numpy(train_lab).long()
    y_hat=net(x)
    loss=criterion(y_hat,y) # 计算损失
    optm.zero_grad() # 前一步的损失清零
    loss.backward() # 反向传播
    optm.step() # 优化
    if (i+1)%100 ==0 : # 这里我们每100次输出相关的信息
        # 指定模型为计算模式
        net.eval()
        test_in=torch.from_numpy(test_data).float()
        test_l=torch.from_numpy(test_lab).long()
        test_out=net(test_in)
        # 使用我们的测试函数计算准确率
        accu=test(test_out,test_l)
        print("Epoch:{},Loss:{:.4f},Accuracy：{:.2f}".format(i+1,loss.item(),accu))

第二节 MNIST识别

没什么好说的，唯一一点把train和test函数封装起来简洁易读，值得学习。

import torch
import torch.nn as nn
import torch.nn.functional as F
from torchvision import datasets,transforms
import torch.optim as optim
batch_size=512
epochs=20
device=torch.device('cuda')
train_loader=torch.utils.data.DataLoader(
    datasets.MNIST('mnistdata',train=True,download=True,
                   transform=transforms.Compose(
                       [transforms.ToTensor(),
                        transforms.Normalize((0.1307,),(0.3081,))])),
    batch_size=batch_size,shuffle=True)
test_loader=torch.utils.data.DataLoader(
    datasets.MNIST('mnistdata',train=False,download=True,
                   transform=transforms.Compose(
                       [transforms.ToTensor(),
                        transforms.Normalize((0.1307,),(0.3081,))])),
    batch_size=batch_size,shuffle=True
)
class ConvNet(nn.Module):
    def __init__(self):
        super(ConvNet,self).__init__()
        self.conv1=nn.Conv2d(1,10,5)
        self.conv2=nn.Conv2d(10,20,3)
        self.fc1=nn.Linear(20*10*10,500)
        self.fc2=nn.Linear(500,10)
    def forward(self, x):
        in_size=x.size(0)
        x=F.relu(self.conv1(x))
        x=F.max_pool2d(x,(2,2))
        x=F.relu(self.conv2(x))
        x=x.view(in_size,-1)
        x=F.relu(self.fc1(x))
        x=F.log_softmax(self.fc2(x),dim=1)
        return x

net=ConvNet().to(device)
optimizer=optim.Adam(net.parameters())

def train(net,device,train_loader,optimizer,epoch):
    net.train()
    for batch_idx,(data,target) in enumerate(train_loader):
        data,target=data.to(device),target.to(device)
        optimizer.zero_grad()
        out=net(data)
        loss=F.nll_loss(out,target)
        loss.backward()
        optimizer.step()
        if batch_idx%100==2:
            print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
                epoch, batch_idx * len(data), len(train_loader.dataset),
                100. * batch_idx / len(train_loader), loss.item()))
def test(net,device,test_loader):
    net.eval()
    test_loss=0
    correct=0
    with torch.no_grad():
        for data,target in test_loader:
            data,target=data.to(device),target.to(device)
            out=net(data)
            test_loss+=F.nll_loss(out,target,reduction='sum').item()
            pred=out.max(1,keepdim=True)[1]
            correct+=pred.eq(target.view_as(pred)).sum().item()
    test_loss /= len(test_loader.dataset)
    print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
        test_loss, correct, len(test_loader.dataset),
        100. * correct / len(test_loader.dataset)))

for i in range(epochs):
    train(net,device,train_loader,optimizer,i)
    test(net,device,test_loader)

第三节 用Sin预测Cos

import torch
import torch.nn as nn
from torch.nn import functional as F
from torch import optim
import numpy as np
from matplotlib import pyplot as plt
import matplotlib.animation
import math, random
TIME_STEP = 10 # rnn 时序步长数
INPUT_SIZE = 1 # rnn 的输入维度
DEVICE = torch.device("cuda" if torch.cuda.is_available() else "cpu") 
H_SIZE = 64 # of rnn 隐藏单元个数
EPOCHS=300 # 总共训练次数
h_state = None # 隐藏层状态
steps = np.linspace(0, np.pi*2, 256, dtype=np.float32)
x_np = np.sin(steps) 
y_np = np.cos(steps)
class RNN(nn.Module):
    def __init__(self):
        super(RNN, self).__init__()
        self.rnn = nn.RNN(
        input_size=INPUT_SIZE,
        hidden_size=H_SIZE, 
        num_layers=1, 
        batch_first=True,
        )
        self.out = nn.Linear(H_SIZE, 1)
    def forward(self, x, h_state):
         # x (batch, time_step, input_size)
         # h_state (n_layers, batch, hidden_size)
         # r_out (batch, time_step, hidden_size)
        r_out, h_state = self.rnn(x, h_state)
        outs = [] # 保存所有的预测值
        for time_step in range(r_out.size(1)): # 计算每一步长的预测值
            outs.append(self.out(r_out[:, time_step, :]))
        return torch.stack(outs, dim=1), h_state
         # 也可使用以下这样的返回值
         # r_out = r_out.view(-1, 32)
         # outs = self.out(r_out)
         # return outs, h_state
rnn = RNN().to(DEVICE)
optimizer = torch.optim.Adam(rnn.parameters()) # Adam优化，几乎不用调参
criterion = nn.MSELoss() # 因为最终的结果是一个数值，所以损失函数用均方误差

rnn.train()
plt.figure(2)
for step in range(EPOCHS):
    start, end = step * np.pi, (step+1)*np.pi # 一个时间周期
    steps = np.linspace(start, end, TIME_STEP, dtype=np.float32)
    x_np = np.sin(steps) 
    y_np = np.cos(steps)
    x = torch.from_numpy(x_np[np.newaxis, :, np.newaxis]) # shape (batch, time_step, input_size)
    y = torch.from_numpy(y_np[np.newaxis, :, np.newaxis])
    prediction, h_state = rnn(x, h_state) # rnn output
    # 这一步非常重要
    h_state = h_state.data # 重置隐藏层的状态, 切断和前一次迭代的链接
    loss = criterion(prediction, y) 
    # 这三行写在一起就可以
    optimizer.zero_grad() 
    loss.backward() 
    optimizer.step() 
    if (step+1)%20==0: #每训练20个批次可视化一下效果，并打印一下loss
        print("EPOCHS: {},Loss:{:4f}".format(step,loss))
        plt.plot(steps, y_np.flatten(), 'r-')
        plt.plot(steps, prediction.data.numpy().flatten(), 'b-')
        plt.draw()
        plt.pause(0.01)