空间关系
变化始于相遇,所以交点是一切的核心。
相交判定
首先考察一束光线能否打在某个平面镜上。光线被抽象成了一个列表[a,b,c],平面镜则被抽象成为由两个点构成的线段[(x1,y1),(x2,y2)]。两条直线的交点问题属于初等数学范畴,需要先将线段转换成直线的形式,然后再求交点。但是两条直线的交点可能落在线段的外面,从而不具有判定的意义。
如果我们的光学系统中有大量的光学元件,那么如果有一种方法可以快速判断光线是否与光学元件有交点,将会显得更加快捷。那么,如果一个直线穿过某个线段,就意味着这条线段的两个端点必然在直线的两侧。
import numpy as np
def isCross(abc,dots):
abc = np.array(abc) #将abc的格式转成数组
flag1 = abc.dot(list(dots[0])+[1]) #数组的点积
flag2 = abc.dot(list(dots[1])+[1])
return flag1*flag2
我们非常熟悉运算符"+",不过目前来说,只有数值和数组是支持加法运算的。所以,对于list(dots[0])+[1]这种表示着实让人有些摸不到头脑。
这个含义其实是符合人类直觉的。列表内的元素个数是可变的,两个列表相加可以理解为两个列表衔接在一起。当然,元组并不支持这种运算。
例如
>>> [1,2,3]+[4] [1, 2, 3, 4] >>> (1,2,3)+(4) Traceback (most recent call last): File "", line 1, in TypeError: can only concatenate tuple (not "int") to tuple
通过加法运算符来衔接两个列表,实际上相当于新建了一个变量,需要开辟新的内存空间。好在对于初学者来说这样不容易出错。
在numpy中,+、-、*、/这几个运算符表示对应位置元素的运算。如果想使用点乘等其他运算,需要调用numpy中的其他函数。
>>> np.array([1,2,3])*np.array([4,5,6])
array([ 4, 10, 18])
>>> np.array([1,2,3])+np.array([4,5,6])
array([5, 7, 9])
>>> np.array([1,2,3]).dot([4,5,6]) #.dot表点积
32
所以, f l a g 1 = [ a , b , c ] ⋅ [ x 0 , y 0 , 1 ] = a x 0 + b y 0 + c 当然,我们也可以写成flag1 = abc[0]*dots[0][0]+abc[1]*dots[0][1]+c,只是看上去不太优雅。
然后,得到了flag1和flag2的值,如果二者异号,那么就可以断定,直线在两个点的中间。也就是说,只要flag1*flag2<0,即可说明直线与线段有焦点。
当然,从实际的角度出发,我们可以不去考虑光线通过镜片的端点或者平行镜片并掠过这种情况,从而只要函数返回值小于零,就认定二者相交,否则不相交。然而,从数学的角度出发,直线和线段之间可能存在三种关系:不相交、有一个交点、线段在直线上。
虽然这个理解没什么实际价值,但对于python学习来说,却是非常有意义的一个例子,代码如下,看懂了这个代码,那么就差不多可以算是一个初级的python程序员了。
def isCross(abc,dots):
abc = np.array(abc)
flags = [abc.dot(list(p)+[1]) for p in dots] #for表达式
poses,negs,zeros = [0,0,0]
for flag in flags: #循环语句
if flag > 0: #判断语句
poses += 1
elif flag <0:
negs += 1
else:
zeros += 1
return poses*negs+zeros
这个短短的程序涵盖了循环语句、判断语句以及for表达式的内容,前两者是最基础的编程知识,后者是python中非常亮眼的一种功能。
首先来认识一下运算符+=,poses += 1即为poses = poses + 1,即相当于将poses+1赋值给poses。赋值前后flag1在内存中的位置发生了变化,也就是说flag1已经不是原来的flag1了。在这里,等号也并不能读成等于,而是读成被赋值为。即poses被赋值为poses+1。前面略有提过,双等号==才表示真正的相等。
然后来看判断语句,对于表达式if a A elif b B else C,我们按照人类的语法去读即可:如果a成立,则执行A,如果b成立,则执行B,否则的话执行C。在上述代码中,也可以很方便地读成:如果flag>0,那么poses被赋值为poses+1;如果flag<0,那么negs变成negs+1;否则的话zeros变成zeros+1。
这几个变量顾名思义,poses表示正数的个数,negs表示负数的个数,zeros表示0的个数。
然后来看[abc.dot(list(p)+[1]) for p in dots],我们首先使用一种没有陌生字符的方式书写:
#这是伪代码,假设dots中有n个变量,表示创建flag1、flag2一直到flagn一共n个变量。 flag1 = abc.dot(list(dots[0])+[1]) flag2 = abc.dot(list(dots[1])+[1]) ... flagn = abc.dot(list(dots[n])+[1])
这个表达式非常规律,这n个变量相当于是在dots中循环一遍,然后逐个赋值。for p in dots表示的就是将dots中的元素取出,赋值给p,然后再对p进行操作abc.dot(list(p)+[1]),最后将所有操作得到的值包裹再一个list中。
最后再记一下这个表达形式 [abc.dot(list(p)+[1]) for p in dots],以后会经常用到。
最后来看for flag in flags,即拿出flags中的所有元素,循环操作其下方的代码块。flags中的元素即为两个点分别带入 a x + b y + c 之后的值。那么对于这两个点来说,如果一正一负,则poses*negs=1*1=1,此时代表直线和线段有一交点,否则这个值便为0。当poses*negs==0时,则zeros的个数表示端点与直线相交的个数,zeros为0,表示无交点,为1,表示有一个端点在直线上,为2表示两个端点都在直线上。
射线排序
现在,我们可以判断某一个线段与一条直线是否有交点了,那么如果空间中有多个平面镜,光线所在的直线又与许多平面镜有交点,那么应该如何找到最近的那个呢?最简单的方法是分别求取这些点到光源的距离,距离越近相交越早。但这样会产生一个问题,即难以判定这个最近点是否在光的传播路径上,如果这个点在光源的后面,那就比较尴尬了。
所以,比较稳妥的方法是,按照射线的方向对所有点进行排序,那么光源后面的那个点,就是光线传播过程中的第一个交点。
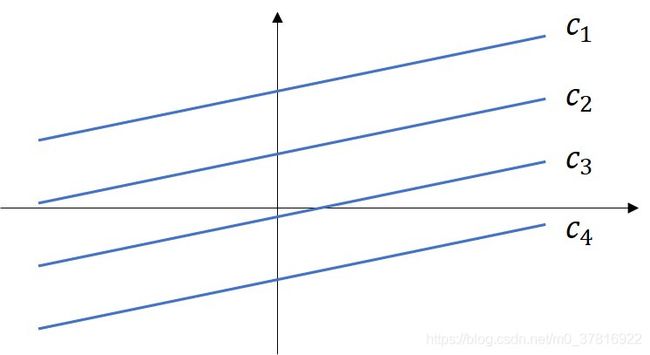
刚刚我们在判定直线与线段的交点时,提到了直线族的概念。发现对于a、b取值相同的一组直线来说,其c值的大小与直线族的顺序是密切相关的。如Fig2-2所示。其 c 1 到 c 4依次递减。
这启发我们需要构建出一组和光线想垂直的直线族[a,b,~],则对于空间中任意一点 ( x , y )其所对应的 a x + b y 的值即能够对射线上的点进行排序。
考虑到a、b的值可能为0,所以不适合求倒数,故采用[b,-a]作为特征直线族,用以评价点在射线上的位置,最终代码如下。
def sortByRay(abc,points):
ab = np.array([abc[1],-abc[0]]) #特征直线族
pDict = {ab.dot(point):point for point in points}
keyList = list(pDict.keys()) #将pDict的兼职转化成列表
keyList.sort(reverse=True) #对键列表进行排序
return [pDict[key] for key in keyList]
这里又涉及到了一个新的数据类型,即字典。在理解字典之前,我们可以先回顾一下列表,我们可以把列表想象成一组值和自然序列的一一对应。对于列表test = [a,b,c,d]来说,有如下的对应关系{0:a,1:b,2:c,3:d},所以我们可以通过test[0]来索引a,test[1]来索引b,以此类推。
那么,现在我不想用自然数来索引了,我想通过一个标记来索引,所以希望能够创建一个伪列表
dic = {3:5,4:15,12:22},于是我们可以对此列表进行索引dic[3]==5,dic[4]==15,dic[12]==22。
这个伪列表就可以由字典来实现。这种索引关系就叫做键值对,我们通过一个键来索引一个值。
对于表达式pDict = {ab.dot(point):point for point in points}
表示通过point对points进行遍历,即对于每个points中的point都进行ab.dot(point)这样的点乘操作。于是得到了由特征直线族得到的特征值与点之间的一一对应关系。
pDict.keys()即可提取出字典中所有的键,pDict.values()可以提取出字典中所有的值。在此我们将所有的键提取出来之后,再将其转化为列表。
然后即可调用列表的排序函数,将所有的值进行排序。即keyList.sort(),其中reverse参数默认为False,此时为降序。我们选择True,此时表示升序。
线弧关系
目前,我们已经能够精确地衡量射线与线段之间的关系了,接下来需要思考如何确定射线与透镜的位置关系。这一点当然也要从交点说起。
首先,弧是圆的一部分,所以如果一条直线与弧有交点,那么必然与这段弧所在的圆有交点。而直线与圆的交点判定相对来说还是非常容易的,只要圆心到直线的距离小于半径即可。
而直线和圆的交点问题则可以归结为求解方程组:
# abc为光线参数;cir为圆参数
# point为光源位置,当其为[]时表示不考虑
def getCrossCircle(abc=[1,1,1],cir=[0,0,2],point=()):
c=np.array(cir[0:2]+[1]).dot(abc)
a2b2 = abc[0]**2+abc[1]**2
delt = a2b2*cir[2]**2-c**2
if delt<0: return [] #如果无交点,返回空列表[]
else: delt=np.sqrt(delt) #否则求解判别式
plusMinus = lambda a,b : np.array(set([a-b,a+b])) #定义函数plusMinus
yCross = plusMinus(-abc[1]*c,abc[0]*delt)/a2b2*[1,1]+cir[1]
xCross = plusMinus(-abc[0]*c,-abc[1]*delt)/a2b2*[1,1]+cir[0]
if point==[]:
return [(xCross[i],yCross[i]) for i in [0,1]]
yFlag = (yCross-point[1])*abc[0] >= 0
xFlag = (point[0]-xCross)*abc[1] >= 0
zFlag = np.abs(xFlag)+np.abs(yFlag) > 0
flag = yFlag*xFlag*zFlag
return [(xCross[i],yCross[i])
for i in range(len(yFlag)) if flag[i]]
这段程序虽然短,但信息量还是很大的,而且使用了一个lambda表达式。
plusMinus = lambda a,b : np.array([a-b,a+b])定义了一个名为plusMius的函数
这个函数写成常规形式即为:
def plusMinus(a,b)
return np.array([a-b,a+b])
需要注意的是,lambda表达式的后面只能有一个表达式,即只能定义一行的函数。
在这段代码中,我们还看到了一个陌生的运算符set,这也是python的一种数据类型,集合。和我们数学上认识的集合一样,在集合中,不允许出现相同的值。所以,如果b==0的话,那么set(a,a)=set(a),即起到了去重的作用。然后再通过np.array将集合转换成可计算的数组数据。
此外,这里引入了比较运算符。我们目前所提到的运算都是数值型的,但实际上我们所接触到的运算还有其他的类型。例如,当我们进行判断的时候,if delt<0:中,<也是一种运算符,代表比较,如果delt的确小于0,那么将返回一个值True,否则自然返回一个False。其中,True表示真,False表示假,这个是符合上过英语课的小学生的直觉的。
类似的运算符有>,<,>=,<=,==,!=,都可以望文生义地理解,其中!=表示不等于。这些都是比较运算符,其返回值为True和False。True和False是一种不同于数值的数据类型,叫布尔型。
关系运算符不仅可以作用于数值类型,还可以作用于其他数据类型,一般情况下的使用方法都是符合直觉的。
>>> 1==2
False
>>> [3,3]==[3,3]
True
>>> 3>3
False
>>> 3>=3
True
然后我们再来看这个算法的逻辑,由于我们求解的是直线和圆的交点,而真实的光线却是射线,那么必然要考虑交点和光源的位置关系。
故代码
yFlag = (yCross-point[1])*abc[0] >= 0 xFlag = (point[0]-xCross)*abc[1] >= 0
分别定义了这两个判据xFlag、yFlag。但是当二者同时为0时,说明此时 x = x 0 , y = y 0 x=x_0,y=y_0 x=x0,y=y0,此时交点即光源,故不能算作光线与圆有交点。所以又有判据zFlag。
只有当这三个判据都满足时,我们所得到的值才是有效的,故总判据与这三个分判据是'与'的关系,所以写为flag = yFlag*xFlag*zFlag。
此外,我们并不知道交点的个数,当判别式为0的时候,lambda表达式将只有一个值传出,这时的xCross和yCross中分别只有一个元素;如果判别式大于0,则分别有两个元素。这里又涉及到array的一个优良特性,当维度不想等的两个变量进行计算时,其会自动对低维数据进行合理的扩张,例如
>>> np.array([1,2,3])+4
array([5, 6, 7])
>>> np.array([[1],[2],[3]])+4
array([[5],
[6],
[7]])
最后,又出现了一个似曾相识的表达式
return [(xCross[i],yCross[i]) for i in range(len(yFlag)) if flag[i]]
这个表达式可以很容易地读出来:遍历flag,如果flag的值为真,则将对应的交点坐标放入列表,并返回有效的交点坐标。
这是对我们之前所使用的[... for ... in ...]的一种扩张,这种写法简洁而强大,非常推荐使用。
点弧关系
一般来说,在一个光学系统中很少出现一整个球,大部分情况下是由部分球面组成的各种透镜。所以,作为二维的光路系统,可能更需要被处理的是光线和圆弧的关系,尤其是和劣弧的关系。
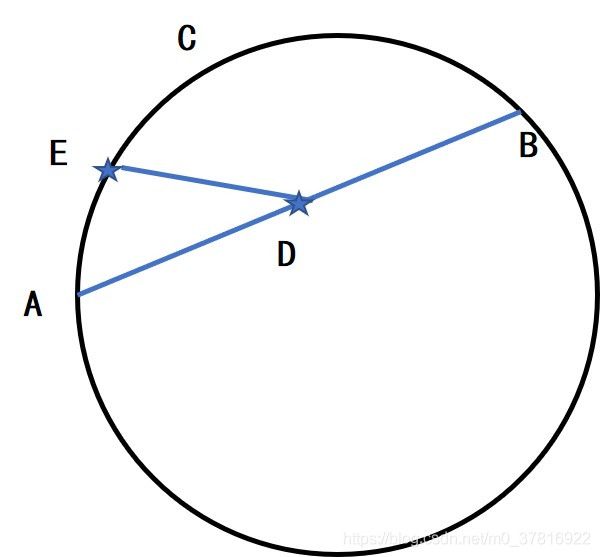
判定点在劣弧上的方法有很多种,例如弧ACB上任意一点关于AB的对称点如果落入圆内,则为劣弧;如果落到园外,则为优弧;如果在圆上,说明AB是直径,弧ACB为半圆。
在此,我们选取另一种方式。如图所示,E为对于劣弧上任意一点,其与AB中点D的连线必然小于AB,否则即在优弧上。
所以,代码为:
def isOnArc(point,arc):
arc = np.array(arc)
dAB = 0.5*np.linalg.norm(arc[0]-arc[1]) #AB/2长度
dCrossA = np.linalg.norm(0.5*(arc[0]+arc[1])-point) #ED长度
return dAB > dCrossA
因此,当满足劣弧判定时,线圆交点即为线弧交点。
def getCrossArc(abc=[1,1,1],arc=[[0,1],[0,-1],[1,0]],point=[]):
if point == []:
return []
crossDict = {np.sqrt((p[0]-point[0])**2+(p[1]-point[1])**2):p
for p in getCrossCircle(abc,arc2cir(arc),point)
if (isOnArc(p,arc) and (p!=point))}
if crossDict == {}:
return []
return crossDict[min(crossDict.keys())]
机灵的同学其实很早就注意到,在定义函数的时候,其传入参数竟然被赋了值。这在python中并不值得大惊小怪,此时输入的值便是默认值。
此外,函数在被调用的时候,我们当然可以通过参数的顺序进行传参,但也可以使用变量名来对参数进行赋值,此时参数的顺序便没有意义了。
例如,
test1 = getCrossArc([1,1,1],[[0,1],[0,-1],[1,0]],(0,0)]
test2 = getCrossArc(abc=[1,1,1],point=(0,0),
arc=[[0,1],[0,-1],[1,0]])
上述两种写法都能得到正确的结果。
以上就是python光学仿真实现光线追迹之空间关系的详细内容,更多关于python实现光线追迹的空间关系的资料请关注脚本之家其它相关文章!