scikit-image库--小波降噪(九）

小波降噪

小波去噪依赖于图像的小波表示。高斯噪声往往由小波域中的小值表示，可以通过将低于给定阈值的系数设置为零（硬阈值）或将所有系数收缩为零（软阈值）来消除。
在这个例子中，我们演示了两种不同的小波系数阈值选择方法：Bayesshrink和Visushrink。

Visushrink算法

Visushrink方法对所有小波细节系数采用一个单一的通用阈值。该阈值用于去除高概率的加性高斯噪声，这种加性高斯噪声往往导致图像过于平滑。通过指定一个小于真实噪声标准偏差的西格玛，可以得到一个更直观的令人满意的结果。

Bayesshrink算法

Bayesshrink算法是小波软阈值的一种自适应方法，它对每个小波子带估计一个唯一的阈值。这通常会导致对单个阈值所能获得的结果的改进。

import matplotlib.pyplot as plt

from skimage.restoration import (denoise_wavelet, estimate_sigma)
from skimage import data, img_as_float
from skimage.util import random_noise
from skimage.measure import compare_psnr


original = img_as_float(data.chelsea()[100:250, 50:300])

sigma = 0.12
noisy = random_noise(original, var=sigma**2)

fig, ax = plt.subplots(nrows=2, ncols=3, figsize=(8, 5),
                       sharex=True, sharey=True)

plt.gray()

# Estimate the average noise standard deviation across color channels.
sigma_est = estimate_sigma(noisy, multichannel=True, average_sigmas=True)
# Due to clipping in random_noise, the estimate will be a bit smaller than the
# specified sigma.
print("Estimated Gaussian noise standard deviation = {}".format(sigma_est))

im_bayes = denoise_wavelet(noisy, multichannel=True, convert2ycbcr=True,
                           method='BayesShrink', mode='soft')
im_visushrink = denoise_wavelet(noisy, multichannel=True, convert2ycbcr=True,
                                method='VisuShrink', mode='soft',
                                sigma=sigma_est)

# VisuShrink is designed to eliminate noise with high probability, but this
# results in a visually over-smooth appearance.  Repeat, specifying a reduction
# in the threshold by factors of 2 and 4.
im_visushrink2 = denoise_wavelet(noisy, multichannel=True, convert2ycbcr=True,
                                 method='VisuShrink', mode='soft',
                                 sigma=sigma_est/2)
im_visushrink4 = denoise_wavelet(noisy, multichannel=True, convert2ycbcr=True,
                                 method='VisuShrink', mode='soft',
                                 sigma=sigma_est/4)

# Compute PSNR as an indication of image quality
psnr_noisy = compare_psnr(original, noisy)
psnr_bayes = compare_psnr(original, im_bayes)
psnr_visushrink = compare_psnr(original, im_visushrink)
psnr_visushrink2 = compare_psnr(original, im_visushrink2)
psnr_visushrink4 = compare_psnr(original, im_visushrink4)

ax[0, 0].imshow(noisy)
ax[0, 0].axis('off')
ax[0, 0].set_title('Noisy\nPSNR={:0.4g}'.format(psnr_noisy))
ax[0, 1].imshow(im_bayes)
ax[0, 1].axis('off')
ax[0, 1].set_title(
    'Wavelet denoising\n(BayesShrink)\nPSNR={:0.4g}'.format(psnr_bayes))
ax[0, 2].imshow(im_visushrink)
ax[0, 2].axis('off')
ax[0, 2].set_title(
    ('Wavelet denoising\n(VisuShrink, $\sigma=\sigma_{est}$)\n'
     'PSNR=%0.4g' % psnr_visushrink))
ax[1, 0].imshow(original)
ax[1, 0].axis('off')
ax[1, 0].set_title('Original')
ax[1, 1].imshow(im_visushrink2)
ax[1, 1].axis('off')
ax[1, 1].set_title(
    ('Wavelet denoising\n(VisuShrink, $\sigma=\sigma_{est}/2$)\n'
     'PSNR=%0.4g' % psnr_visushrink2))
ax[1, 2].imshow(im_visushrink4)
ax[1, 2].axis('off')
ax[1, 2].set_title(
    ('Wavelet denoising\n(VisuShrink, $\sigma=\sigma_{est}/4$)\n'
     'PSNR=%0.4g' % psnr_visushrink4))
fig.tight_layout()

plt.show()

PSNR（Peak Signal to Noise Ratio）峰值信噪比，是一种全参考的图像质量评价指标。

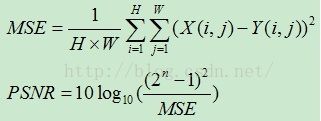
其中，MSE表示当前图像X和参考图像Y的均方误差（MeanSquare Error），H、W分别为图像的高度和宽度；n为每像素的比特数，一般取8，即像素灰阶数为256. PSNR的单位是dB，数值越大表示失真越小。

PSNR是最普遍和使用最为广泛的一种图像客观评价指标，然而它是基于对应像素点间的误差，即 基于误差敏感的图像质量评价。由于并未考虑到人眼的视觉特性（人眼对空间频率较低的对比差异敏感度较高，人眼对亮度对比差异的敏感度较色度高，人眼对一个 区域的感知结果会受到其周围邻近区域的影响等），因而经常出现评价结果与人的主观感觉不一致的情况。

PSNR高于40dB说明图像质量极好（即非常接近原始图像），

在30—40dB通常表示图像质量是好的（即失真可以察觉但可以接受），

在20—30dB说明图像质量差；

最后，PSNR低于20dB图像不可接受