《剑指offer》专题—算法训练 day03
文章目录
- 《剑指offer》专题—算法训练day03
- 一、青蛙跳台阶
-
- 思路
- 二、矩形覆盖
-
- 思路
- 三、链表中倒数第k个结点
-
- 思路
- 四、二进制中1的个数
-
- 思路一
- 思路二
- 思路三
- 未完待续...
《剑指offer》专题—算法训练day03
接着上一篇我们提到的 斐波那契数列,我们来 简单了解一下 动态规划问题
现阶段我们解决动归问题,只需要了解三个步骤
1.定义状态
2.编写状态转移方程
3.设置初始值
下面我们通过两道题,也就是《青蛙跳台阶》、《矩形覆盖》两个部分进行深入实践
一、青蛙跳台阶
https://www.nowcoder.com/practice/8c82a5b80378478f9484d87d1c5f12a4?
思路
定义状态
我们可以根据题意得到
如果 青蛙要跳到 n 级台阶的跳法怎么算
我们已知青蛙 一次能跳 1级台阶 或者 2级台阶,所以青蛙最后一步要么跳2节(从n-2开始跳),要么跳1节(从n-1开始跳),我们可得 跳到 n级台阶的跳法 = 跳到(n-1)级台阶的跳法 + 跳到(n-2)级台阶的跳法
得到状态转移方程
f(n) = f(n-1)+f(n-2)
设置初始值
我们知道 青蛙从第0级台阶开始跳,跳到1级有一种跳法 f(1) = 1 ,跳到2级有两种跳法 f(2) = 2,跳到三级 就有 3种方法 ,f(3 ) = f(1) +f(2) = 3…
所以我们根据这些条件,可以编写相关代码了
相关代码
public class Solution {
public int jumpFloor(int target){
if(target ==0||target == 1 || target == 2){
return target;
}
return jumpFloor(target-1) +jumpFloor(target-2);
}
}
二、矩形覆盖
https://www.nowcoder.com/practice/72a5a919508a4251859fb2cfb987a0e6?
思路
这个题的思路和上面青蛙跳台阶基本一致,我们还是再来分析一下吧
我们可以发现,就是如果我们 最后 如果要 覆盖成一个 2*n 的矩形,最后一步的方法,可以一次放1个竖的,要么直接放2个横的
所以 覆盖2*n矩形的方法 = 覆盖 2 *(n-1) 的所有方法 + 覆盖 2 *(n-2)的所有方法
我们得到了状态转移方程
f(n) = f(n-1)+f(n-2)
然后开始设置初始值
n=0时 方法有0种
f(0 ) = 0
n=1时 方法有1种 (竖的放一个)
f(1)= 1
n=2时 方法有2种 (竖的放两个、或者横的放两个)
f(2) = 2
n=3时,方法有三种,如题中所给的那三种方法
f(3) = 3
根据上述的相关条件,我们可以编写这道题的代码了
public class Solution {
public int rectCover(int target) {
// 这个题最后去放时,要么放一个竖的,要么放两个横的
if(target == 0){
return 0;
}
if(target==1){
return 1;
}
if(target==2){
return 2;
}
return rectCover(target-2)+rectCover(target-1);
}
}
三、链表中倒数第k个结点
https://www.nowcoder.com/practice/529d3ae5a407492994ad2a246518148a?
思路
举一个例子:
我先提供一个 已有的链表结构
![]()
我们现在提供 给一个整形参数 k = 2 ,找到这个链表结构中的倒数第二个节点 。
思路一
![]()
思路二
![]()
这种思路我们在实际链表中 走一遍…
设置 fast 、slow 指向head 头节点
![]()
fast 先走 k-1 步, slow 保持不动
![]()
slow、fast 同时向后走,直到 fast 为指为null
![]()
此时 slow 指向的就是 我们题目所求的链表的 倒数第 2 个节点。
返回 slow。
好的 思路二能够找到倒数第 K 个节点,我们来就具体实现其每一个步骤的具体思路
1.首先我们传入参数 k 值,要考虑 k的合法性
2.slow、fast 的实际操作
![]()
但是 ,上面的代码思路仍然有缺陷,在判断 k 的合法性时, 如果 k > sizeof() ,我们要调用 sizeof() 函数,此时也是一次 遍历链表的过程,所以 遍历次数两遍,也不符合要求。
我们还要继续调整…
![]()
![]()
这样的思路过程就没有问题了,整体代码遍历一遍。
相关代码
/*
public class ListNode {
int val;
ListNode next = null;
ListNode(int val) {
this.val = val;
}
}*/
public class Solution {
public ListNode FindKthToTail(ListNode head,int k) {
// 先对参数的合法性进行判断
if(head == null){
return null;
}
if(k<=0){
return null;
}
// k 的合法值应该在[0,size] 之间 (size 是链表的长度)
// 但是为了题解时间复杂度的尽可能小,我们先不对链表进行遍历求长度.
// 定义 两个 快慢指针 进行辅助
ListNode fast = head;
ListNode slow = head;
while(k>0){
// 如果fast 成为 null ,说明 k的大小超过了链表的长度,k值非法,那么直接返回一个 null
if(fast == null){
return null;
}
// fast 不为 null 时,快指针先往后走 k 个节点
fast = fast.next;
k--;
}
// fast 先走了k 个节点,然后 fast 和 slow 一起向后遍历.
// 当 fast为null 时,slow 对应的节点就是 倒数第 k 个节点.
while(fast !=null){
fast = fast.next;
slow = slow.next;
}
// 此时返回slow
return slow;
}
}
四、二进制中1的个数
https://www.nowcoder.com/practice/8ee967e43c2c4ec193b040ea7fbb10b8?
思路一
从n的2进制形式的最右边开始判断是不是1,该解法如果输入时负数会陷入死循环,因为负数右移时,在最高位补得是1,在题中最终目的是求1的个数,那么会有无数个1了。
-------------可能陷入死循环的解法---------------------
public class Solution {
public int NumberOf1(int n) {
int count= 0;
while(n!=0){
if((n&1)== 1){
count++;
}
n >>= 1;
}
return count;
}
}
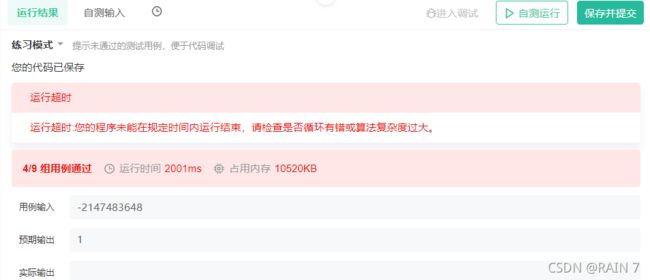
运行结果:
遇到负数循环过多导致运行超时
思路二
所以我们知道题目中给我们提供的都是整形int,一共有32位,所以我们要控制循环的次数
public class Solution {
public int NumberOf1(int n) {
int count= 0;
for(int i =0;i<32;i++){
if((n&1)== 1){
count++;
}
n >>= 1;
}
return count;
}
}
思路三
public class Solution {
public int NumberOf1(int n) {
int count= 0;
while(n!=0){
count++;
n = n & (n-1);
}
return count;
}
}
分析一下代码:
这段小小的代码,很是巧妙。
如果一个整数不为0,那么这个整数至少有一位是1。如果我们把这个整数减1,那么原来处在整数最右边的1就会变为0,原来在1后面的所有的0都会变成1(如果最右边的1后面还有0的话)。其余所有位将不会受到影响。
好了,今天的内容就结束了,希望大家多多练习~~
谢谢欣赏!!!
《剑指offer》 算法训练day4 敬请期待…