【路径规划-VRP问题】基于蚁群算法求解带时间窗车辆路径规划问题(VRPTW)matlab源码
1 简介
随着电子商务的发展,其便利快捷的购物特性,让越来越多的人们选择网上购物这种方式,电商在人们生活中占据越来越重要的位置。由于其远距离特性,因此需要物流行业在其中起着配送的作用。由于在物流业务中,快递普遍成本过高并且效率低下,因此提高运送效率和降低快递成本对于降低网购成本具有很大的现实意义,车辆路径规划问题(Vehicle Routing Problem,VRP)是公认的解决物流配送问题求解最低货物成本的理论模型。货物配送服务的关键是服务速度和质量,在一个给定的期间内,一组客户和一组车辆,这些车辆被分配到一个或更多集运点。通过对一个车队来进行约束操作并使用适当的公路网络,VRP问题的解被称为确定的一组路线,每个车辆的起点和终点都在自己的集运点。如此,所有的客户都被满足,所有的操作约束都被满足,并且整体的运输费用最低。在过去的数十年中对快递优化方案正在逐渐增加,大量现实实例证实,使用大量的计算机程序应用于规划分配计划中,可以在整体运输成本中产生大量的节约(通常较不做规划节约5%-20%)。很容易看出来,这些节约在整体行业成本中是很重大的,事实上,运输过程包括生产和分配系统的全过程。并且运输成本也是最终成本的相关因素。车辆路径规划问题的研究可以减少很大一部分物流开销。到目前为止,出现了很多求解车辆路径问题的算法,有精确算法(accurate algorithm)和启发式算法(heuristicsalgorithms)。其中,精确算法用来求解问题最优解的方式是严格的数学方法,启发式算法则利用对状态空间的位置评价来找到较好的位置,再基于这个位置进行搜索,直到找到目标为止。随着问题规模不断地扩大,精确算法的计算量越来越大,还不能直接用来解决实际问题。启发式算法则可以根据不同的问题要求来求解问题。基于VRP问题的本质,不太可能使用精确的方法求解VRP的大规模的实例。因此,大部分方法都依赖于启发式方法来获取近似解。许多方法已经被用到了这个领域中,其中有选择使用标准优化技术的算法,例如,蚁群算法、遗传算法、模拟退火和约束编程。我们在这里关注于元启发式算法,主要是蚁群算法。蚁群算法是启发式算法中主流的一种算法。由Marco Dorigo于1992年受到蚂蚁觅食行为启发而提出,将其应用到了组合优化问题中。通过实验结果表明,蚁群算法可以找到相对较好的解,而且具有很强的鲁棒性。
2 部分代码
clear
clc
close all
tic
%% 用importdata这个函数来读取文件
c101=importdata('c101.txt');
cap=200; %车辆最大装载量
%% 提取数据信息
E=c101(1,5); %配送中心时间窗开始时间
L=c101(1,6); %配送中心时间窗结束时间
vertexs=c101(:,2:3); %所有点的坐标x和y
customer=vertexs(2:end,:); %顾客坐标
cusnum=size(customer,1); %顾客数
v_num=25; %车辆最多使用数目
demands=c101(2:end,4); %需求量
a=c101(2:end,5); %顾客时间窗开始时间[a[i],b[i]]
b=c101(2:end,6); %顾客时间窗结束时间[a[i],b[i]]
width=b-a; %顾客的时间窗宽度
s=c101(2:end,7); %客户点的服务时间
h=pdist(vertexs);
dist=squareform(h); %距离矩阵
%% 初始化参数
m=60; %蚂蚁数量
alpha=1; %信息素重要程度因子
beta=3; %启发函数重要程度因子
gama=2; %等待时间重要程度因子
delta=3; %时间窗跨度重要程度因子
r0=0.5; %r0为用来控制转移规则的参数
rho=0.5; %信息素挥发因子
Q=5; %更新信息素浓度的常数
Eta=1./dist; %启发函数
Tau=ones(cusnum+1,cusnum+1); %信息素矩阵
Table=zeros(m,cusnum); %路径记录表
iter=1; %迭代次数初值
iter_max=100; %最大迭代次数
Route_best=zeros(iter_max,cusnum); %各代最佳路径
Cost_best=zeros(iter_max,1); %各代最佳路径的成本
%% 迭代寻找最佳路径
while iter<=iter_max
%% 先构建出所有蚂蚁的路径
%逐个蚂蚁选择
for i=1:m
%逐个顾客选择
for j=1:cusnum
r=rand; %r为在[0,1]上的随机变量
np=next_point(i,Table,Tau,Eta,alpha,beta,gama,delta,r,r0,a,b,width,s,L,dist,cap,demands);
Table(i,j)=np;
end
end
%% 计算各个蚂蚁的成本=1000*车辆使用数目+车辆行驶总距离
cost=zeros(m,1);
NV=zeros(m,1);
TD=zeros(m,1);
for i=1:m
VC=decode(Table(i,:),cap,demands,a,b,L,s,dist);
[cost(i,1),NV(i,1),TD(i,1)]=costFun(VC,dist);
end
%% 计算最小成本及平均成本
if iter == 1
[min_Cost,min_index]=min(cost);
Cost_best(iter)=min_Cost;
Route_best(iter,:)=Table(min_index,:);
else
[min_Cost,min_index]=min(cost);
Cost_best(iter)=min(Cost_best(iter - 1),min_Cost);
if Cost_best(iter)==min_Cost
Route_best(iter,:)=Table(min_index,:);
else
Route_best(iter,:)=Route_best((iter-1),:);
end
end
%% 更新信息素
bestR=Route_best(iter,:);
[bestVC,bestNV,bestTD]=decode(bestR,cap,demands,a,b,L,s,dist);
Tau=updateTau(Tau,bestR,rho,Q,cap,demands,a,b,L,s,dist);
%% 打印当前最优解
disp(['第',num2str(iter),'代最优解:'])
disp(['车辆使用数目:',num2str(bestNV),',车辆行驶总距离:',num2str(bestTD)]);
fprintf('\n')
%% 迭代次数加1,清空路径记录表
iter=iter+1;
Table=zeros(m,cusnum);
end
%% 改进蚁群结果显示
bestRoute=Route_best(end,:);
[bestVC,NV,TD]=decode(bestRoute,cap,demands,a,b,L,s,dist);
figure
hold on;box on
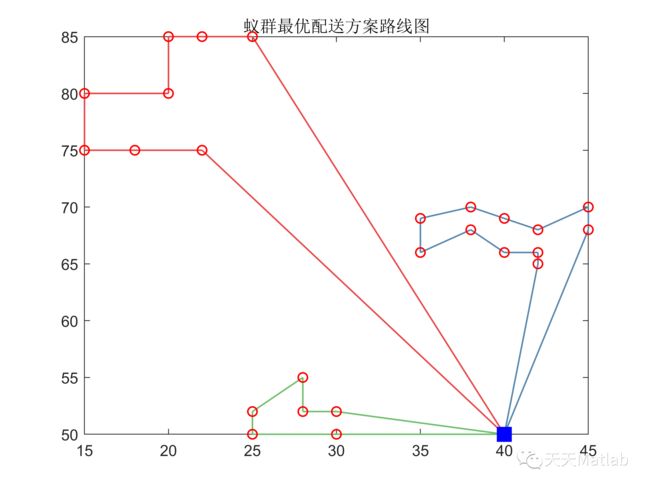
title('蚁群最优配送方案路线图')
hold on;
disp('蚁群路径方案')
draw_Best(bestVC,vertexs);
img =gcf; %获取当前画图的句柄
print(img, '-dpng', '-r600', './img.png') %即可得到对应格式和期望dpi的图像
%% 绘图
figure
plot(1:iter_max,Cost_best,'b')
xlabel('迭代次数')
ylabel('成本')
title('各代最小成本变化趋势图')
img =gcf; %获取当前画图的句柄
print(img, '-dpng', '-r600', './img1.png') %即可得到对应格式和期望dpi的图像
%% 判断最优解是否满足时间窗约束和载重量约束,0表示违反约束,1表示满足全部约束
flag=Judge(bestVC,cap,demands,a,b,L,s,dist);
%% 检查最优解中是否存在元素丢失的情况,丢失元素,如果没有则为空
DEL=Judge_Del(bestVC);
toc
3 仿真结果
4 参考文献
[1]辛颖. 基于蚁群算法的车辆路径规划问题求解研究[D]. 吉林大学.![]()