五、OpenCV-python 之图像处理（Ⅲ）——傅里叶变换

一、傅里叶变换是啥？

1、数学定义

若 $f(x)$ 为非周期函数，在 $x$ 的整个周期内满足狄里赫利条件，则 $f(x)$ 可以用叠加积分表示：
$$f(x)=\underset{-\infty }{\overset{\infty }{\int }}F(u)e^{j2\pi ux}du$$

2、实质

从定义可以看到，一个复杂的函数可以表示为很多个简单函数的和（积分就是求和），把它放到信号处理场景中就是：傅里叶变换可以将一个信号分离为无穷多正弦/复指数信号的加成。

3、意义

对于一些有时间变化规律的信号，例如周期信号，人们发现用频率 w 来描述它比用时间 t 来描述它更为高效，所以需要将时域信号转换为频域信号。

傅里叶变换可以将一个时域信号转换成在不同频率下对应的振幅及相位，反傅里叶变换可以将频谱再转换回时域的信号。

二、具体应用

1、声音信号处理

对有杂音的声音音频数据做傅里叶变换，得到一个展开式，找出杂音的频率，去掉展开式中对应频率的函数项，然后还原数据，就可以去除杂音！

2、图像处理

对有噪点的图片数据做傅立叶变换，得到一个展开式，将高频函数的系数增大，然后还原图像就可以提高图像的对比度。

三、OpenCV 之傅里叶变换

OpenCV 的傅里叶变换可以用来分析各种滤波器的频率特征。

我们将图像视作在两个方向上采样的信号，分别在这两个方向上做傅里叶变换，就能获取图像的频率特征。一般，对于一个正弦曲线的信号而言，我们可以将它表示为 $x(t)=A\ast sin(2\pi ft)$，$A$ 是振幅，$f$ 是频率，当 $f$ 很大时就是高频信号，$f$ 较小时就是低频信号。同样的思想可以应用于图像，图像中边缘和噪点处的变化快、频率高，所以它们是高频特征；相反，变化慢、相对平坦的区域就是低频特征。

1、傅里叶变换的基本步骤

拿滤波来举例：

• DFT：对输入图像做傅里叶变换，得到频域图谱（低频域位于图谱左上角）
• Shift：将频域图谱做偏移，使得低频域位于图谱的正中心
• Filter：通过掩码完成滤波，高通滤波就是中心为0，周边为1；低通滤波就是中心为1，周边为0
• inverse-DFT：将频域图谱再次偏移，使得中心位置回到图谱的左上角，恢复图像

上述操作就使得图像中的低频特征被过滤掉，只剩下高频特征，可以用来检测图像边缘。

2、OpenCV 的实现

OpenCV 中提供直接计算傅里叶变换的函数 cv.dft，它接收 np.float32 灰度图，输出同等尺寸双通道数组，第一个通道是傅里叶变换结果的实部，第二个通道是傅里叶变换结果的虚部。有了实部和虚部之后，就可以计算振幅，cv.magnitude 就是用来计算矢量振幅的，可以用 matplotlib 画出频谱图。

import numpy as np
import cv2 as cv
from matplotlib import pyplot as plt

img = cv.imread('messi5.jpg',0)															# cv.dft 需要接受灰度图

dft = cv.dft(np.float32(img),flags = cv.DFT_COMPLEX_OUTPUT)								# cv.dft 需要接受 np.float32 数据
dft_shift = np.fft.fftshift(dft)														# 位置偏移 shift

magnitude_spectrum = 20*np.log(cv.magnitude(dft_shift[:,:,0], dft_shift[:,:,1]))		# 计算矢量振幅

plt.subplot(121),plt.imshow(img, cmap = 'gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(magnitude_spectrum, cmap = 'gray')
plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])

plt.show()

上述代码实现了前两步：DFT 和 shift，后面需要完成滤波操作。要做滤波我们先要创建一个掩码，以低通滤波为例，掩码中心 60*60 的区域（低频域）像素值为1（让它通过），其他区域（高频域）像素值为0（阻止通过），将掩码和频谱图做元素级别的矩阵乘法即可。

# 低通滤波的掩码，中心为1
rows, cols = img.shape
crow,ccol = rows/2 , cols/2
mask = np.zeros((rows,cols,2), np.uint8)
mask[crow-30:crow+30, ccol-30:ccol+30] = 1

# 掩码和 DFT 相乘
fshift = dft_shift*mask

# 再次偏移，恢复至左上角
f_ishift = np.fft.ifftshift(fshift)

# DFT 的逆变换，恢复图像
img_back = cv.idft(f_ishift)
img_back = cv.magnitude(img_back[:,:,0],img_back[:,:,1])

plt.subplot(121),plt.imshow(img, cmap = 'gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(img_back, cmap = 'gray')
plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])

plt.show()

以上就是利用傅里叶变换完成低通滤波的完整过程，可以看到低通滤波过滤掉了边缘、噪点这些高频特征，使图像变得模糊。如果仔细观察结果，会看到模糊后的图像中有一些伪影（红圈内图像），它显示了一些类似波纹的结构，这被称为振铃效应；这是由我们用来遮蔽的矩形窗口造成的，所以一般矩形窗口不用于过滤，更好的选择是高斯窗口。

3、傅里叶变换的性能优化

傅里叶变换需要数组形式的输入，当数组大小是 2 的幂时是最快的，大小为2、3和5的乘积的数组也被相当有效地处理。所以，可以在做 DFT 之前给图像做像素值为0的 padding。OpenCV 提供一个 cv.getOptimalDFTSize() 函数，可以快速返回优化后的图像尺寸。

img = cv.imread('messi5.jpg', 0)
rows,cols = img.shape
nrows = cv.getOptimalDFTSize(rows)
ncols = cv.getOptimalDFTSize(cols)

right = ncols - cols
bottom = nrows - rows
bordertype = cv.BORDER_CONSTANT
nimg = cv.copyMakeBorder(img, 0, bottom, 0, right, bordertype, value=0)	# 添加 padding

上述代码可以和之前没做尺寸优化的代码进行对比，性能提速在4倍以上。

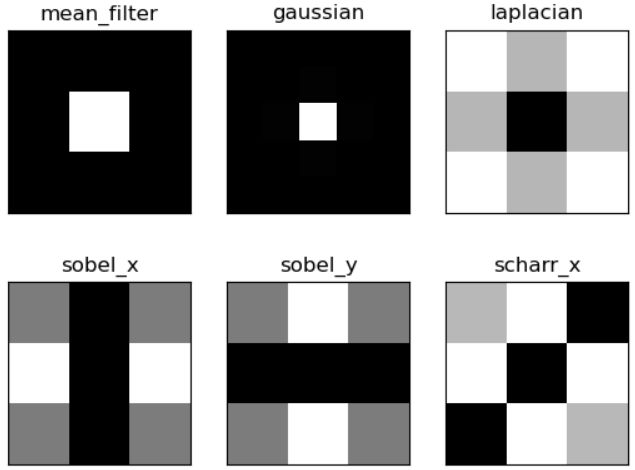
4、为什么 Laplacian 是高通滤波？

其实这个问题应该改为：如何通过傅里叶变换判断一个滤波器是高通滤波还是低通滤波？

import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt

# 均值滤波器
mean_filter = np.ones((3,3))

# 高斯滤波器
x = cv.getGaussianKernel(5,10)
gaussian = x*x.T

# scharr_x
scharr = np.array([[-3, 0, 3],
                   [-10,0,10],
                   [-3, 0, 3]])

# sobel_x
sobel_x= np.array([[-1, 0, 1],
                   [-2, 0, 2],
                   [-1, 0, 1]])

# sobel_y
sobel_y= np.array([[-1,-2,-1],
                   [0, 0, 0],
                   [1, 2, 1]])

# laplacian
laplacian=np.array([[0, 1, 0],
                    [1,-4, 1],
                    [0, 1, 0]])

filters = [mean_filter, gaussian, laplacian, sobel_x, sobel_y, scharr]
filter_name = ['mean_filter', 'gaussian','laplacian', 'sobel_x', 'sobel_y', 'scharr_x']
fft_filters = [np.fft.fft2(x) for x in filters]
fft_shift = [np.fft.fftshift(y) for y in fft_filters]
mag_spectrum = [np.log(np.abs(z)+1) for z in fft_shift]

for i in xrange(6):
    plt.subplot(2,3,i+1),plt.imshow(mag_spectrum[i],cmap = 'gray')
    plt.title(filter_name[i]), plt.xticks([]), plt.yticks([])
plt.show()

laplacian 中心区域为黑色表示不通过，周边为灰色或白色，表示通过，所以是高通滤波。