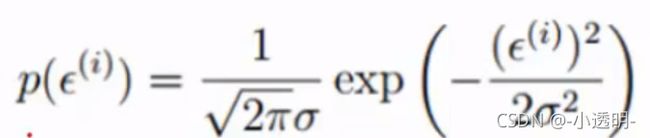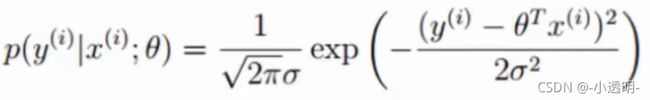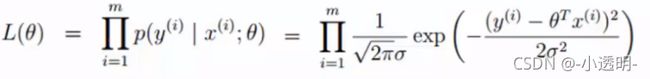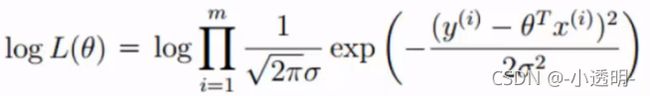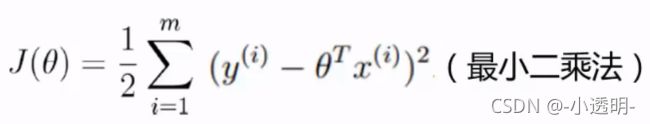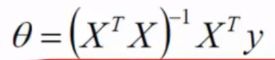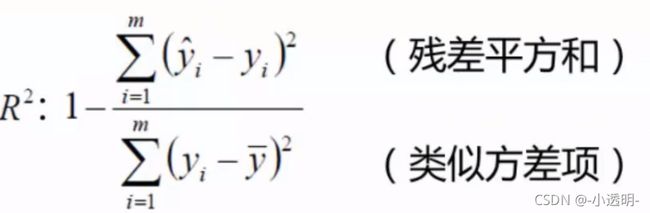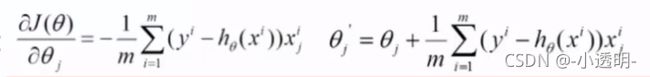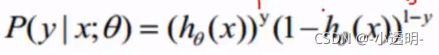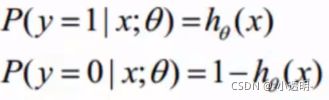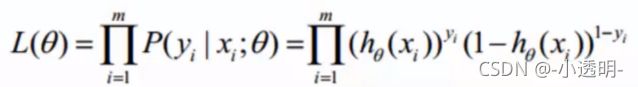Python数据分析与机器学习实战＜六＞线性回归算法
目录
算法概述
一个例子（线性回归）
下面数学来了！
误差项分析
似然函数求解
似然函数（最大的似然估计）
对数似然
目标函数
线性回归求解
目标函数求偏导
评估方法（高中就学过）
梯度下降原理
梯度下降方法对比
批量梯度下降
随机梯度下降
小批量梯度下降
学习率对结果的影响
逻辑回归
Logistic regression
Sigmoid函数
预测函数
逻辑回归求解
似然函数
对数似然
求偏导 i:第i个样本；j：第j个特征
参数更新
多分类的softmax(先知道后面神经网路会细讲)
总结
算法概述
线性回归算法是机器学习中最简单也是最基础的一个算法。要会用也要理解为何。
机器学习有监督算法分为两种：回归和分类。
回归：通过数据预测一个值，最终得到区间中一个确定的值。
分类：（已知有总共多少类），最终得到一个类别值。
一个例子（线性回归）
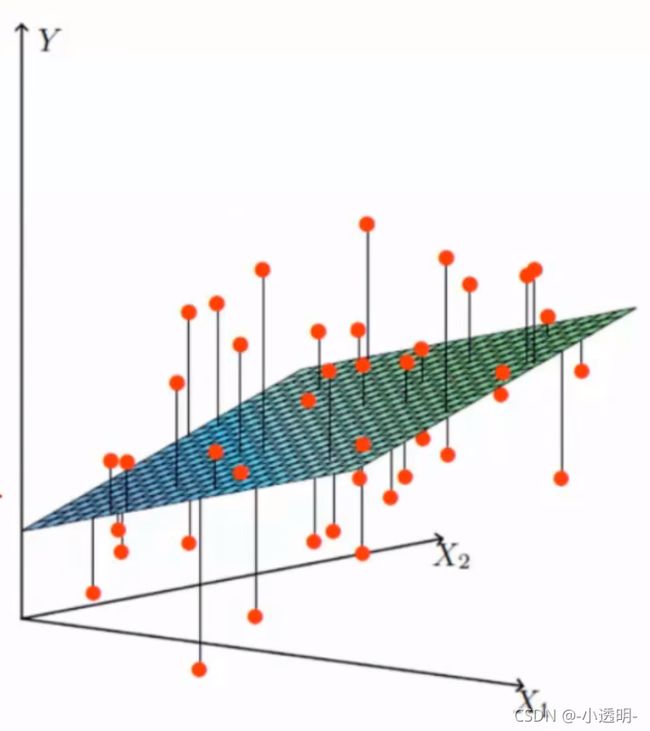
数据：工资和年龄（两个特征）
目标：预测银行会贷给我多少钱（标签）
考虑：工资和年龄都会影响最终银行贷款的结果，那么他们各自的影响有多大呢？（参数）
下面数学来了！
不必具备所有数学知识。学到哪里不会再去搜就可以了。
假设
1是年龄的参数，2是工资的参数
拟合的平面:
（θ0是偏执项）
整合：（当有n个特征时）
（x0=1,额外增加一个特征,为了矩阵的运算）
将数据转换成标准的矩阵格式 
误差项分析
误差：真实值和预测值之间肯定存在误差（用
表示）。如上图所示，拟合平面与真实的值（点）
* 对每个样本：
线性回归中一个非常非常非常核心的概念（一定要理解）
机器学习中的模型建立：从实际情况触发做一个假设(没有数学的严格证明),但只要服从基本的规则，这个模型就是可用的。
* 误差
是独立且具有相同分布的，并且服从均值为0，方差为
的高斯分布（假设均值为零：因为实际可能多可能少，取个平均，就假设为0；均值为0了那自然方差就为了）
* 独立：张三和李四一起来贷款，他俩没关系。（即每个样本是独立的）
* 同分布：他俩是同一家银行。
* 高斯分布：银行可能会给多或给少，但绝大多数情况下浮动不会太大，极少情况浮动较大，符合实际情况。（大多数情况下，不仅是这一个例子，其他例子中都会假设服从高斯分布，因为高斯分布是符合现实情况的。可以这么理解，正态分布就是正常情况下它的大致分布。）
* 由于误差服从高斯分布（写公式太麻烦了，下面我就直接截图了）
将 用θ表示，带入上式得：
似然函数求解
似然函数（最大的似然估计）
：根据样本估计参数值的函数。（即参数估计）
更形象的解释：即什么样的参数跟数据组合后恰好是真实值
在这里要明白两点：
1. 为什么数据要和参数组合？
因为 我们有这样一个预测值
2. 为什么概率越大越好？
因为当然希望组合完之后越接近实际越好啦
对数似然
上面的似然函数是一个累乘，乘法是太难天难了，加法就容易多啦，因此
似然函数转换成对数似然，对数里的乘法就可以变成加法啦！log默认以e为底
对上示展开化简得：
目标：让似然函数（变换成对数似然也一样）越大越好。上述式子减号左边为恒一个正数（一个常数），右边也是一个大于零的数 ，因此让右边的式子越小越好。
目标函数
提到线性回归，这三个问题一定要懂：（总结一下）
1. 为什么要有似然函数？
因为我想让我设的参数带入以后跟真实值差别不大，为了找这样的参数而引入的。
2 为什么又要引入对数似然?
因为似然函数是做乘法，太复杂，为了简化运算，而引入对数似然
3. 为什么J(θ)越小越好？
因为对数似然函数中减号左边为恒一个正数，右边也是一个大于零的值 ，因此让右边的式子越小越好。
线性回归求解
目标函数求偏导
机器学习中：
凸优化概念：普遍认为目标函数是一个凸函数，因此，令偏导等于0得到的是极小值。
令偏导等0得：
（大多数情况都是可解的）
评估方法（高中就学过）
最常用的评估项 （越接近1越好）
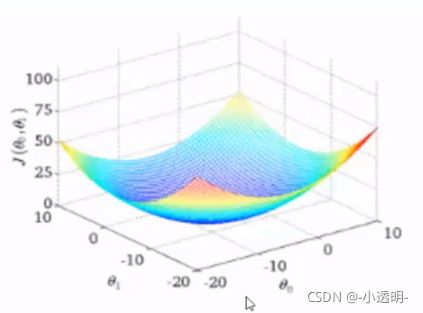
梯度下降原理
这里推荐 吴恩达的machine learning
[中英字幕]吴恩达机器学习系列课程_哔哩哔哩_bilibili（还没看完，有空会做笔记滴）暑假时候看的，距离现在有点久远了，所以这个相当于回顾一下之前看的内容吧。
机器学习常规套路：我交给机器一堆数据，然后告诉它什么样的学习方式是对的（目标函数），然后让它朝着这个方向去做。
如何优化？迭代（通常1万到10万次差不多）
J(θ1，θ2)函数
下降：沿着某一方向，合适的步长下降到最低点即为目标函数的最小值。
梯度下降方法对比
批量梯度下降
批量：虽然容易得到最优解。但缺点也是很明显的，由于每次考虑所有样本（计算量很大）迭代一次耗费时间很长，速度慢，无法进行多次迭代。
随机梯度下降
随机：每次找一个样本，迭代速度快，但不一定每次都朝着收敛的方向。
小批量梯度下降
每次更新选择一小批数据，实用！
学习率对结果的影响
学习率（步长）：对结果会产生巨大的影响，一般小一点。太大可能会越过最小值。
一般：用小的学习率进行学习，用大的迭代次数进行迭代。
实验时，先拿0.01试，不够小的话再缩小
批处理数量：32 64（一般） 128都可以，还要考虑内存和速率（能大点就大点，最后结果稳定）
逻辑回归
Logistic regression
* 目的：是一种(最牛的)经典的二分 分类算法！（当然也可以解决多分类问题）
* 机器学习算法选择：先逻辑回归再用复杂的，能简单还是用简单的。
* 逻辑回归的决策边界：可以是非线性的。
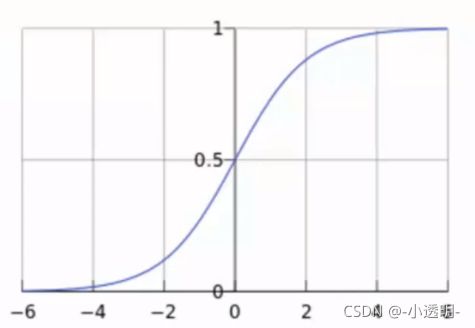
Sigmoid函数
公式：
自变量取值为任意实数，值域[0,1]
解释：将任意的输入映射到了[0,1]区间，我们在线性回归中可以得到一个预测值，再将该值映射到这个函数中。这样就完成了值到概率的转换，这就是分类任务！
预测函数
其中：
分类任务整合：
逻辑回归求解
似然函数
对数似然
求偏导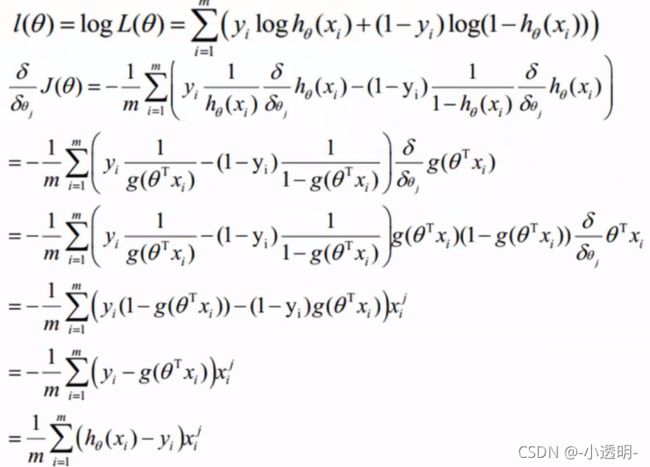
i:第i个样本；j：第j个特征
参数更新
1）首先找到最合适的方向
2）步长（学习率α）小一点沿着方向走
3）按照方向和步长更新参数
α：学习率
多分类的softmax(先知道后面神经网路会细讲)
总结
逻辑回归真的很好很好用！