第七章：神经网络与神经语言模型_Dan Jurafsky《自然语言处理综述》(第三版)读书笔记

7.0前言

神经网络是语言处理中核心的计算工具，并且很早就出现了。神经这个名字最早来源于McCulloch-Pitts neuron(1943)，是一个人类神经元的简化模型，可以理解为命题逻辑中的计算单元（？）？。不过现在在语言处理中，不再具有生物学意义。现在的神经网络是一个小型的由众多计算单元组成的网络，输入一个向量，输出一个值。这章介绍用于分类的神经网络，前馈神经网络，因为计算过程迭代地从前一层传到下一层。现在的神经网络也被称为深度学习，因为现在的网络常常很深，有很多层。
神经网络与逻辑回归有许多相似的数学运算，但是神经网络作为分类器要更为强大，即使只有一个隐藏层的最小的神经网络都可以实现所有函数。神经网络分类器和逻辑回归还有一个不同。使用逻辑回归时，需要根据领域知识设计很多特征，然后应用于分类任务中。而使用神经网络，通常是避免使用人工设计的特征，而是直接将词语输入神经网络，在神经网络学习分类的过程时，顺带获得特征。词嵌入就是通过这种方式获得的。所以 深层神经网络特别适合表示的学习，尤其适合使用大规模数据来自动学习特征。
本章将学习前馈神经网络作为分类器，并应用于建立语言模型：计算一个词语序列的概率，预测后词。后面章节将介绍RNN和编码-解码模型。

7.1单元units

神经网络的构成组件是一个简单的计算单元。一个单元把一组实值作为输入，通过计算，输出另一个值。它的核心是将输入进行加权求和，再加上一个偏置项。给定一组输入$x_1...x_n$，这个单元有一组相应的权重$w_1...w_n$，和一个偏置项b，那么加权和$z$可以表示为：$$z=b+\sum _i{w}_i{x}_i$$使用向量表示会更加方便，向量就是一组数字，权重向量为$w$，标量偏置项为$b$，输入向量为$x$，把加权和用内积代替：$$z=w\cdot x+b$$结果$z$是一个实值。不过最后的输出并不是$z$，$z$是$x$的线性函数，神经单元再把$z$传入到一个非线性函数$f$，我们把这个函数的输出称为激活值$a$。上面我们只构造了一个单元，这个节点的激活值就是这个网络的最终输出，我们一般称之为$y$。$$y=a=f(z)$$下面讨论三个常用的非线性函数$f()$：sigmoid，tanh，ReLu。sigmoid有很多的好处，它把输出投射到0到1的空间，还有就是它是可微分的。$$y=\sigma (w\cdot x+b)=\frac{1}{1+exp(-(w\cdot x+b))}$$

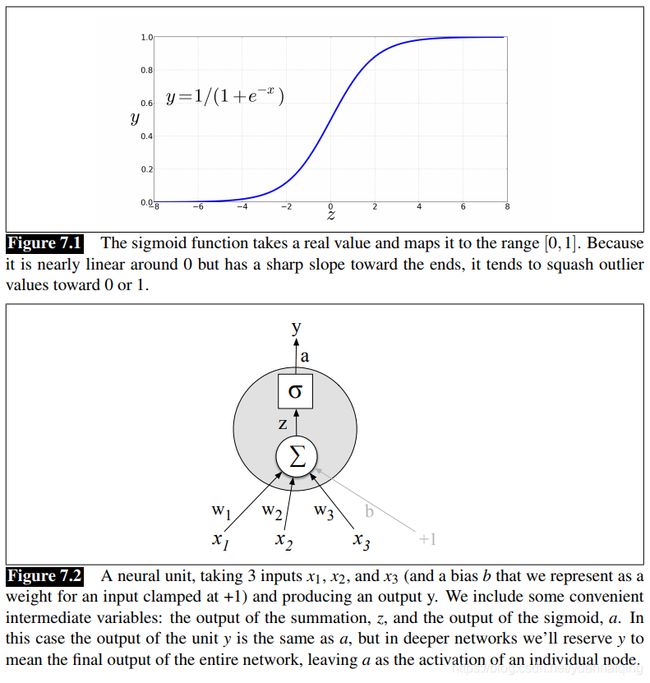
上图，三个特征加一个偏置，输入到神经元中，加权求和后输入sigmoid函数，输出激活值a。

实际上，sigmoid不是常用的激活函数，经常使用的是tanh，与sigmoid相似，但是效果更好。tanh是sigmoid的变体，值域为-1到1：$$y=\frac{e^z-e^{-z}}{e^z+e^{-z}}$$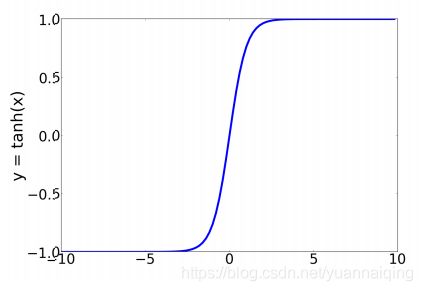
不过，最简单的激活函数，可能是最常用的，是ReLU，也叫修正线性单元。x为正时，函数值为x；x为负时，函数值为0：$$y=max(x,0)$$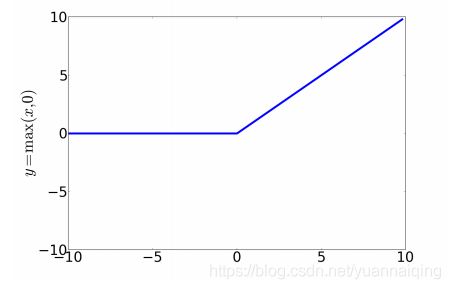
激活函数的不同性质，会在不同的语言应用或者网络架构中起到不同作用。ReLU使它的输出结果趋向于线性。sigmoid和tanh中，如果输入的z值较大，那么输出值y就会趋近于1，学习过程会发生问题，ReLU就没有这样的问题，不过tanh的好处是平滑可微，并把离群值映射到均值。

7.2异或问题

早在神经网络的初期，人类就意识到神经网络的力量来源于把多个计算单元连在一起，形成大网络。因为单一的神经元甚至不能解决很简单的逻辑问题。下面看Minsky&Papert（1969）给出的证明：AND, OR, XOR(相同取0，相异取1)问题。
感知机(perception)是一个简单的神经单元，有两个输出，没有非线性激活函数。两个输出分别是0和1：$$y=\{\begin{array}{lc}0,& ifw\cdot x+b\le 0\\ 1,& ifw\cdot x+b>0\end{array}$$我们可以很容易地设计出一个感知机，来计算逻辑AND(a)和OR(b)。

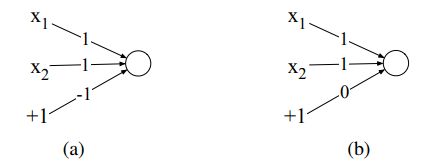
x1和x2是输入，取值0或者1，那么AND的计算结果是x1+x2-1，只有x1=x2=1时，AND的计算结果为1，也就是为真；OR的计算结果是x1+x2，只要x1和x2不全为零，OR的结果就是1或者2，也就是为真。

但是，我们没有办法设计一个能计算XOR问题的感知机！原因是感知机实际上是一个线性分类器。对于一个二维输入x1，x2，感知机公式$w1x1+w2x2+b=0$，实际上是一条直线：$x2=-(w1/w2)x1-b$。这条直线就是二维空间里的决策边界，输入直线一侧的点输出为0，输入直线另一侧的点输出为1。如果我们有2个以上的输入，决策边界将变成一个超平面，不过意义是一样的，也是把空间分成了两个类别。下图展示了在二维空间中，逻辑输入(00, 01, 10, 11)以及AND和OR分类器在设某一组参数时的分界线。但是由于XOR问题不是一个线性可分的问题，所以没法画出线性分界线，不过可以使用曲线画出分界线。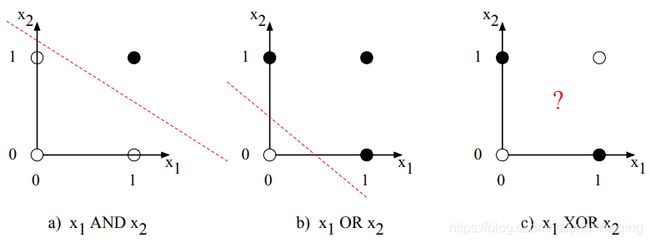

7.2.1解决方案：神经网络

既然XOR不能通过一个感知机来计算，我们可以使用多层网络来解决。Goodfellow(2016)使用基于ReLU的两层神经网络解决了XOR问题。

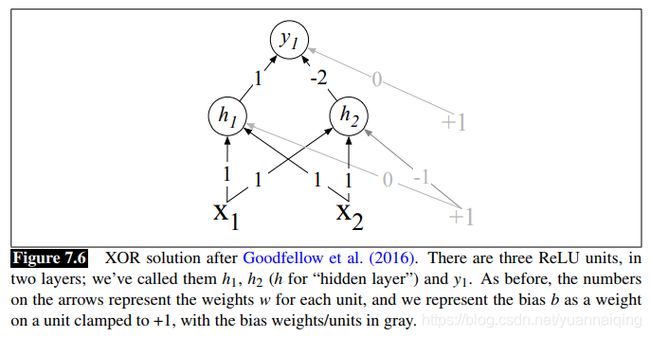
中间层有2个单元，输出层有1个单元。黑色箭头上的数字是权重，灰色箭头为偏置项。我们尝试输入[0, 0]，得到h₁=0，h₂=-1，将ReLU函数分别应用于h₁，h₂，分别得到0和0，也就是[0, 0]，再作为输入计算y₁的值为0。尝试输入[0,1]和[1, 0]，将得到1。这就解决了XOR问题。
回过头来观察一下隐藏层，下图展示了原始输入经过隐藏层变换后的值。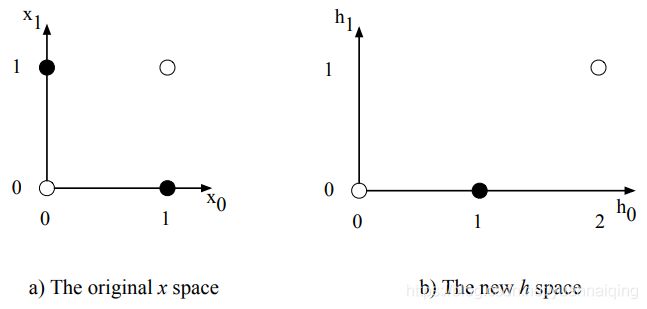
输入[0,1]和[1,0]转换成了[1,0]；[1,1]变成了[2,1]。于是原始的4个点变成了3个线性可分的点。所以，我们可以把隐藏层看作对输入表示的转化。
在以上的例子中，我们直接设定好了网络的权重参数。但是在真正的神经网络中，这些参数是通过错误反向传播算法自动学习到的。也就是说，隐藏层将自动学习对输入表示进行转化的参数，这也是神经网络的一个巨大优势。
注意：要解决XOR问题，网络中的神经元需要用到非线性激活函数。即使多个感知机组成网络，由于它没有非线性激活函数，它也解决不了XOR问题。因为纯线性计算单元组成的多层网络总是能被简化为（或等同于）一个单层感知机，而单层的结构无法解决XOR问题。

7.3前馈神经网络

前馈网络是一个多层网络，神经元之间相连无回路，一层网络的输出，作为输入传到另一层，方向是单一向前的。由于历史的原因，多层网络有时被称为多层感知机(multi-layer perceptions)，实际上是用词不当，因为今天多层网络中的计算单元都有类似sigmoid等的非线性激活函数，而这是感知机所没有的。
简单的前馈网络有三种节点：输入单元、隐藏单元、输出单元。

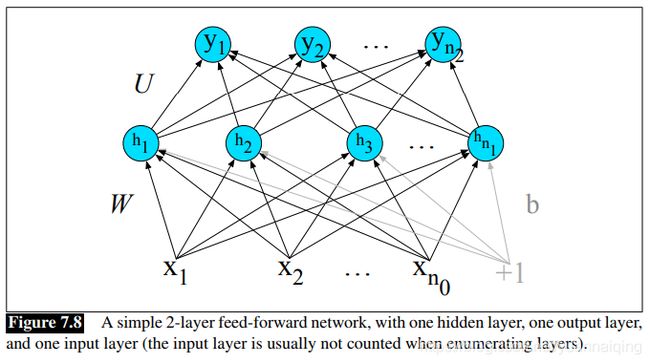
输入单元接受标量数值。神经网络的核心是由隐藏单元构成的隐藏层。隐藏单元接受输入的加权和，然后使用非线性激活函数。在标准的结构中，每一层都是全连接的(fully-connected)，意思是：每一层的每一个单元接受previous层所有单元的输出作为输入；相邻的两层，前层任何一个神经元都有后层任何一个神经元相连接。因此，每个隐藏神经元都对所有的输入单元求和。
隐藏层的每一个单元有参数$w$(权重向量)和一个$b$(偏置项标量)。如果把一个隐藏层的所有单元的权重向量$w_i$和偏置项$b_i$堆叠到一起，那么每一个隐藏层的所有权重可以表示为矩阵$W$，所有偏置项组成向量$b$。矩阵中的每一个元素$W_{ij}$表示输入单元$x_i$到隐藏单元$h_j$的权重。使用一个矩阵$W$储存整层权重的好处是：前馈网络隐藏层的计算可以非常快。计算只有三步：输入向量$x$乘以权重矩阵；加上偏置向量$b$；传入激活函数$g$求得隐藏层的输出$h$：$$h=\sigma (Wx+b)$$注意：这里的$\sigma$函数用到了一个向量上，激活函数$g(\cdot )$用于向量上时表示：$g[z_1,z_2,z_3]=[g(z_1),g(z_2),g(z_3)]$.
我们引入一些常量来表示上面向量和矩阵的维数。我们把网络的输入层称为第0层，用n₀来表示输入的数量，那么x就是一个维度为n₀的实数向量，或者说$x\in {\mathbb{R}}^{n_0}$。我们把隐藏层称为第1层，输出层称为第2层。隐藏层的维度为n₁，那么$h\in {\mathbb{R}}^{n_1}$而且$b\in {\mathbb{R}}^{n_1}$，因为每一个隐藏层单元都有一个不同的偏置项。那么权重矩阵W的维度就是$W\in {\mathbb{R}}^{n_1\times n_0}$。
从上面的7.2可以看出来，隐层h的值实际上是输入的一种表示，输出层就是使用这一个新的表示h，计算出最终结果。最终结果可以是一个实数，但在更多的情况下神经网络的目标是做出某种分类决策，所以这里我们也重点关注分类。
如果我们做二分类任务，例如情感分类，我们只需要一个输出单元，它的输出值y是积极情感的概率。如果我们做的是多分类任务，比如词性标注，那么我们可能就需要为每一个词性设置一个输出单元，输出值就是这个词性的概率，并且所有输出单元的输出值总和为1。也就是说，输出层给出了所有输出单元的概率分布。
来看一下计算过程。输出层也有一个权重矩阵U，不过有一些简化的模型没有偏置向量b，我们就也使用简化模型来说明。权重矩阵乘以输入向量h，得到一个值z。$$z=Uh$$假如输出层有n₂个单元，那么$z\in {\mathbb{R}}^{n_2}$，权重矩阵U的维度为$U\in {\mathbb{R}}^{n_2\times n_1}$，元素U_ij是隐藏层第j个神经元到输出层第i个神经元的权重。
不过需要注意的是，现在z并不是分类器的最终输出结果，因为z是一个实数向量，而我们需要的是概率向量。有一个很方便的函数可以将实数向量标准化为概率分布，也就是所有的值处于0到1之间，而且总和为1：它就是softmax函数。对于d维的向量z，softmax的定义为：
$$softmax(z_i)=\frac{e^{z_i}}{{\sum }_{j=1}^d{e}^{z_j}}1\le i\le d$$
因此，如果 z = [0.6 1.1 -1.5 1.2 3.2 -1.1]，softmax(z) = [ 0.055 0.090 0.0067 0.10 0.74 0.010]。这和逻辑回归里的softmax使用方法一样。
所以我们可以这样来解释含有一个隐藏层的神经网络分类器：先把输入通过隐藏层表示为向量h，再把这个向量作为特征，传入标准的逻辑回归中来计算得到结果。比较逻辑回归和神经网络，逻辑回归需要通过特征模板人工设计特征，而神经网络虽然很像逻辑回归，但不同的是（a）有很多层，深度神经网络的结构就像多个逻辑回归分类器连在一起，（b）无需人工设计特征，最初的网络层可以自己形成特征的表示。
那么含有一个隐藏层的前馈神经网络最终的公式是：
$h=\sigma (Wx+b)$
$z=Uh$
$y=softmax(z)$
这种网络被称为2层网络，传统上输入层不被当作一层。因此逻辑回归也可以称为单层网络。
对于超过2层的深度网络，我们用上标方括号来表示层数，0还是表示输入层。那么$W^{[1]}$表示第1层（隐藏层）的权重矩阵，$b^{[1]}$表示第1层的偏置向量。$n_j$表示第 j 层的单元数量。我们用$g(\cdot )$表示激活函数，中间层的激活函数为ReLu或者tanh，输出层的激活函数为softmax。使用$a^{[i]}$表示第i层的输出，$z^{[i]}$表示线性计算结果$W^{[1]}{a}^{[i-1]}+b^{[i]}$，第0层为输入，所以输入 $x$ 一般写作 $a^{[0]}$。
例如，3层网络的计算过程为：
$z^{[1]}=W^{[1]}{a}^{[0]}+b^{[1]}$
$a^{[1]}=g^{[1]}(z^{[1]})$
$z^{[2]}=W^{[2]}{a}^{[1]}+b^{[2]}$
$a^{[2]}=g^{[2]}(z^{[2]})$
$\hat{y}=a^{[2]}$
同理，给定输入 $a^{[0]}$， n 层前馈神经网络的前向算法为：

for i in 1…n
  $z^{[i]}=W^{[i]}{a}^{[i-1]}+b^{[i]}$
  $a^{[i]}=g^{[i]}(z^{[i]})$
$\hat{y}=a^{[n]}$

其中，最后一层的激活函数 $g(\cdot )$ 一般是不同的。输出层的激活函数，二分类的话用sigmoid，多分类的话用softmax；隐藏层的激活幻术用ReLu或者tanh。

7.4 训练神经网络

前馈神经网络是有监督的机器学习，每一个观察 $x$ 对应一个真实结果 $y$ 。网络系统的输出为$\hat{y}$，也就是对 $y$ 的预测。训练的目标是：学习每一层的权重矩阵$W^{[i]}$和偏置向量$b^{[i]}$，使得$\hat{y}$尽可能地接近 $y$。
训练的方法与逻辑回归的训练类似。第一，我们需要一个损失函数来对系统输出和真实结果的距离建模，常用的还是交叉熵损失函数(cross-entropy loss)。第二，找到参数来最小化损失函数，我们使用梯度下降优化算法。第三，使用梯度下降需要知道损失函数的梯度，求损失函数关于每个参数的偏导，这些偏导组成一个向量，这个向量就是梯度。这里要比逻辑回归复杂，在逻辑回归中，对于每一个观察，我们可以直接关于每个参数 w 和 b 求损失函数导数。但是在有着多个层几百万参数的神经网络就难了，难点在于，如果关于第1层的某些参数求函数导数，但是损失（loss）还与后面各层相关，那我们如何通过众多的中间层求得损失（loss）？（原文：it’s much harder to see how to compute the partial derivative of some weight in layer 1 when the loss is attached to some much later layer. How do we partial out the loss over all those intermediate layers?）
答案是误差反向传播算法（error back-propagation）或者叫反向求导（reverse differentiation）。

7.4.1 损失函数

神经网络中使用的交叉熵损失函数与逻辑回归中一样。实际上，如果使用神经网络进行二分类，输出层用sigmoid，损失函数就是和逻辑回归中完全一样。
$$L_{CE}(\hat{y},y)=-logp(y|x)=-[ylog\hat{y}+(1-y)log(1-\hat{y})]$$
那么当神经网络作为多分类器时，$y$ 就是一个 $C$ 个类别的向量，表示真实结果的概率分布，这时的交叉熵损失就是$$L_{CE}(\hat{y},y)=-\sum _{i=1}^C{y}_i\log {\hat{y}}_i$$我们可以进一步简化这个公式。假设这是一个硬分类任务(hard classification)，意思是正确的分类结果只有一个，y 中每一类有一个输出单元。如果正确的分类是 i ，那么向量 y 中 y_i=1，其它的元素值都是 0 。这种只有一个值为 1，其他值为 0 的向量，叫做 one-hot 向量。现在令 $\hat{y}$ 作为网络的输出向量，因为除了正确的类别值为 1，其他值都为 0，交叉熵损失函数就被简化成了正确类别的对数概率，也被称为负对数似然损失函数(negative log likelihood loss)：
$$L_{CE}(\hat{y},y)=-log{\hat{y}}_i$$
代入 softmax 的公式，并且类别数为K，得到：
$$L_{CE}(y,y)=-\log \frac{e^{z_i}}{{\sum }_{j=1}^K{e}^{z_j}}$$

7.4.2 计算梯度

那么我们如何来计算损失函数的梯度呢？计算梯度，需要关于每一个参数求损失函数的偏导。对于像逻辑回归一样的网络，只有一个隐层并使用sigmoid输出，我们可以直接使用损失函数的导数：

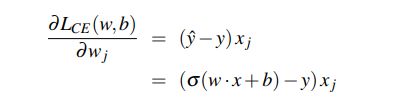
或者对于只有一个隐层并使用softmax输出的网络，我们可以使用softmax损失函数的导数：

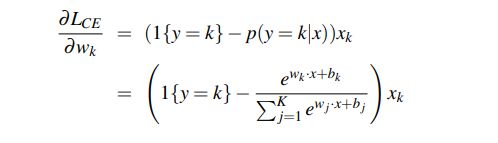
但是这些导数只能用于最后一层的权重更新。对于深度网络，计算每一个权重的梯度要复杂得多，虽然对于损失的计算只涉及最后一层网络，但是关于权重参数的导数的计算要一直回溯到网络的最初层。
解决这个问题的算法叫做误差反向传播。虽然反向传播是针对神经网络发明的，但与一般意义上的的反向求导其实是一样的，反向求导是一种基于计算图（computaion graphs）的算法。

7.4.3 计算图

计算图是数学表达式计算过程的展示，其中计算被分解为多个独立的运算，每个运算被建模为图中节点。
试想我们来计算函数 $L(a,b,c)=c(a+2b)$，我们把加法运算和乘法运算拆分出来，并为中间输出加上名称($d和e$)，那么得到的一系列计算就是：
$$d=2\ast b$$$$e=a+d$$$$L=c\ast e$$
我们现在就可以将上面的计算表示为图了，每一个节点表示一个运算，有向边表示每个运算的输出作为下一个运算的输入。下图展示了计算的向前传播(forward pass)过程。在计算图的向前传播过程中，运算从左至右，将每个运算的输出结果传递到下一节点作为输入。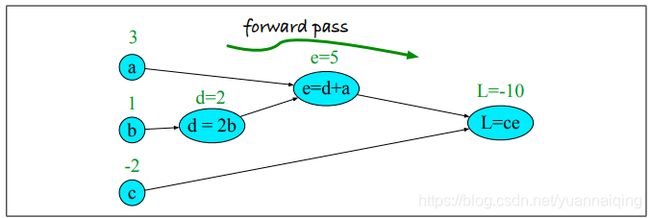

7.4.4 使用计算图进行反向求导

计算图的重要性来自于向后传递(backward pass)，用于计算导数来更新参数。对于上面的例子，我们的目标是：关于所有的输入变量（$\frac{\partial L}{\partial a}，\frac{\partial L}{\partial b}，\frac{\partial L}{\partial c}$）求函数$L$ 的导数。导数$\frac{\partial L}{\partial a}$告诉我们$a$的微小变化如何影响$L$。
反向求导使用微积分中的链式法则（chain rule）。设想我们在计算复合函数$f(x)=u(v(x))$的导数，那么$f(x)$的导数就是$u(x)$关于$v(x)$的导数，乘以$v(x)$关于$x$的导数：
$$\frac{df}{dx}=\frac{du}{dv}\cdot \frac{dv}{dx}$$
链式法则可以扩展到两个以上的函数。如果计算符合函数$f(x)=u(v(w(s)))$的导数，那就是：
$$\frac{df}{dx}=\frac{du}{dv}\cdot \frac{dv}{dw}\cdot \frac{dw}{dx}$$
现在我们来计算我们需要的3个导数。在计算图中，$L=ce$，我们可以直接计算导数$\frac{\partial L}{\partial c}$：
$$\frac{\partial L}{\partial c}=e$$
对于另外两个，我们将用到链式法则：
$$\frac{\partial L}{\partial a}=\frac{\partial L}{\partial e}\frac{\partial e}{\partial a}$$$$\frac{\partial L}{\partial b}=\frac{\partial L}{\partial e}\frac{\partial e}{\partial d}\frac{\partial d}{\partial b}$$
可以看到，上面的等式需要求五个中间导数：$\frac{\partial L}{\partial e},\frac{\partial L}{\partial c},\frac{\partial e}{\partial a},\frac{\partial e}{\partial d},\frac{\partial d}{\partial b}$，因为和的导数等于导数的和，可以求得：

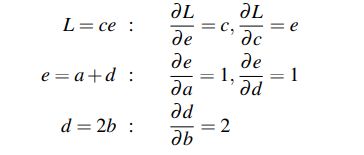
在向后传递过程中，我们沿着计算图的有向边从右到左计算每一个偏导，将我们需要的偏导相乘，得到我们需要的最终导数。因此，我们从最终节点开始，在图上标注$\frac{\partial L}{\partial L}=1$。然后向左走来计算$\frac{\partial L}{\partial c}$和$\frac{\partial L}{\partial e}$以及其它偏导，直到我们一直走到输入层，并标注了全部的偏导。当然，我们需要一些中间值来计算这些导数（比如 d 和 e），还好向前传递的过程早就计算好了这些值。下图展示了向后传递的过程。在每一个节点， 我们需要计算关于其父节点的局部偏导，然后乘以从父节点传过来的偏导，然后再传递给子节点。？

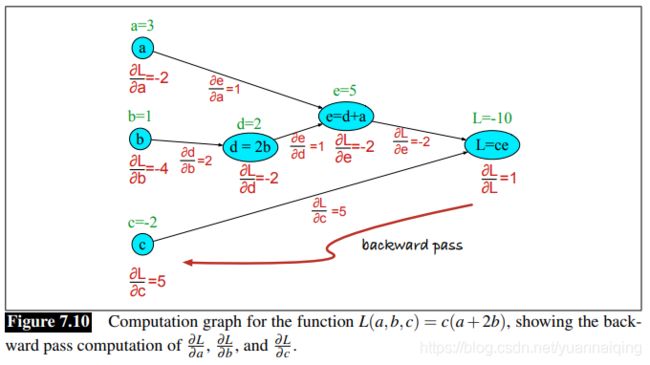
神经网络的反向求导

当然，真正的神经网络的计算图要复杂得多。下图展示了一个两层的神经网络的计算图，其中 n₀=2, n₁=2, n₂=1，使用 sigmoid 作为输出单元进行二分类。计算图中的各项运算如下：

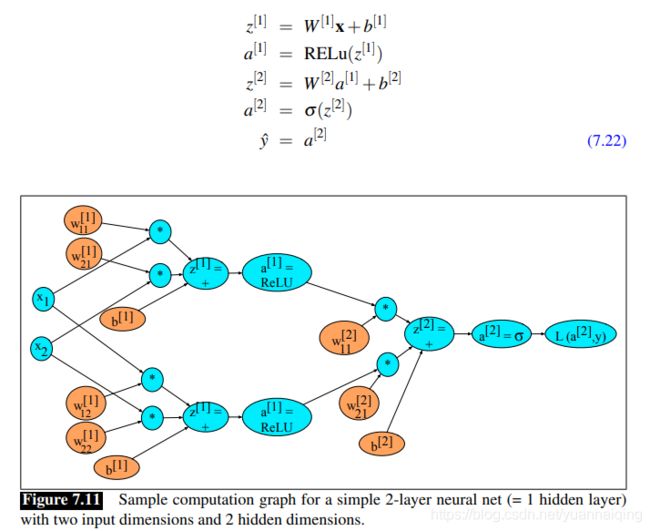
橙色的是需要更新的权重（也就是我们需要计算损失函数偏导的变量）。为了进行反向传递，我们需要知道图中所有函数的导数。我们已经知道 sigmoid 函数的导数是：
$$\frac{d\sigma (z)}{dz}=\sigma (z)(1-\sigma (z))$$
我们还需要其他激活函数的导数。tanh 的导数是：
$$\frac{dtanh(z)}{dz}=1-tan{h}^2(z)$$
ReLu的导数是：
$$\frac{dReLu(z)}{dz}=\{\begin{array}{l}0forx<0\\ 1forx\ge 0\end{array}$$

7.4.5 更多的学习细节

神经网络的优化是一个非凸优化问题，比逻辑回归更复杂，有很多成功的实践。
对于逻辑回归，我们可以初始化所有的权重和偏置为 0 。在神经网络中却相反，我们需要初始化权重为小的随机数。把输入标准化，使均值为零和方差为一，也会很有用。
使用各种形式的正则化可防止过度拟合。最重要的其中一种是dropout：网络训练过程中，随机丢弃一些单元和其连接（Hinton 2012）。调节超参数也很重要。神经网络的参数是权重 W 和偏置项 b ；它们是通过训练得到的。超参数是算法设计人员自己设定的，最优值是在开发集上不断调节得到，而不是在训练集上通过梯度下降得到。超参数包括学习率 $\eta$ ，小批量（mini-batch）的大小，模型架构（层数，每层的隐藏节点数，激活函数的选择），正则化的方法，以及其他。梯度下降本身也有许多架构变体，比如Adam。
最后，大部分现代神经网络是使用计算图来构建的，这样在基于向量的GPU上进行梯度计算和并行化将更加容易和自然。Pytorch和TensorFlow是最流行的两个。

7.5 神经语言模型

我们神经网络的第一个应用是语言建模 (language modeling)：根据前词预测后词。
基于神经网络的语言模型相比于第三章中介绍 的n 元语言模型，有更多优势。比如神经语言模型不需要平滑，可以处理更长的历史信息，and they can generalize over contexts of similar words(并且它们可以概括相似单词的上下文。)?基于给定大小的训练集，神经语言模型比 n 元语言模型在预测上有更高的准确性。此外，神经语言模型是机器翻译、对话、语言生成等任务的基础。
不过，好的表现背后是较高的成本：神经网络要比传统语言模型训练速度慢得多，所以 n 元语言模型对于某些任务来说仍然是首选工具。
本章我们将介绍简单的前馈神经语言模型，最早由 Bengio(2003) 提出。不过目前的神经语言模型通常不是前馈网络而是循环网络 (recurrent)，第九章我们会介绍相关技术。
一个前馈神经语言模型是一个标准的前馈网络，在 t 时刻，输入多个前续词语的表示（$w_{t-1},w_{t-2},$ 等），输出后续可能词语的概率分布。正如 n 元语言模型，前馈神经语言模型通过上文的语境 $P(w_t|w_1^{t-1})$ 估算后面词语的概率，也是基于这样的假设：前面的全部语境概率与 N 个前词的语境概率近似：$$P(w_t|w_1^{t-1})\approx P(w_t|w_{t-N+1}^{t-1})$$下面我们用 4-元语法作为例子，也就是来估算概率 $P(w_t=i|w_{t-1},w_{t-2},w_{t-3})$。

7.5.1 词嵌入

在神经语言模型中，上文语境是用前词的词嵌入来表示的。在 n 元语言模型中，上文语境是用词语本身来表示的，使用词嵌入，使得神经语言模型比 n 元语言模型有更好的泛化能力。比如，我们在训练集中有：I have to make sure when I get home to feed the cat. 但是训练集中如果没有过 “feed the dog”，那么在进行测试的时候，我们如果来预测语境 “I forgot when I got home to feed the” 后面的词语，那么 n 元语言模型会预测为“cat”，不会是“dog”。但是在神经语言模型中，鉴于 cat 和 dog 具有相似的词嵌入，模型就会给 dog 和 cat 同样高的概率，因为他们是相似的向量。
下面看一下这是如何工作的。假设我们有一个通过word2vec预训练得到的词嵌入词典 $E$ ，对于我们词汇表 $V$ 中的任一词汇，都对应一个词嵌入向量。
下图展示了一个简单的前馈神经网络模型，其中 N = 3；我们在 t 时刻有一个窗口，还有前面三个词语的词嵌入向量；这三个向量连接在一起，作为神经网络的输入 x ，网络的输出层为 softmax，输出词汇的概率分布。在输出层的第 42 个几点，表示下一个词 w_t为 $V_{42}$的概率，也就是词汇表中的第 42 个词语。如果我们已经使用 word2vec 的方法得到了所有的词嵌入，那么这个模型就已经是完整的了。使用其他算法来学习输入层的词嵌入表示，被称为预训练。

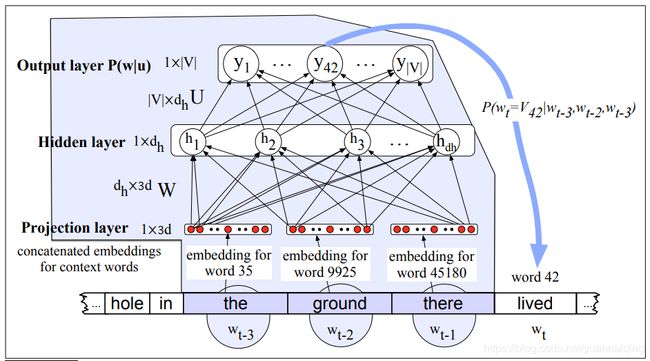
不过，我们常常希望在训练网络的同时得到词嵌入。This is true when whatever task the network is designed for (sentiment classification, or translation, or parsing) places strong constraints on what makes a good representation.
那么我们来看一个可以同时顺便学习词嵌入的结构。我们得额外添加一层，还要把误差一直向后传到词嵌入向量。初始词嵌入为随机值，然后慢慢调整为合理的表示。
需要处理的是输入层， 上文语境有 N 个词语，每一个词语我们都用长度为 $|V|$的 one-hot 向量来表示。one-hot向量是这样的向量：只有一个元素的值为 1，这个元素的位置就是这个单词在词汇表中的位置，其他所有元素的值为 0。因此，toothpaste 的 onehot 表示，假设它在词汇表中的位置是 5，那么它就可以表示为 [ 0 0 0 0 1 0 0…0]，$x_5=1,x_i=0\forall i̸=5$ 。
下图展示了语言模型在训练的时候，学习词嵌入所需要的额外一层。这里 N=3 的上文语境由3个 one-hot 向量表示，同过词嵌入矩阵 $E$ ，与嵌入层进行全连接。注意，我们不想学到3个独立的的权重矩阵来把这3个词分别投射到投射层，我们想使用一个公用的词嵌入词典$E$。因为随着时间点的推移，会有更多不同词作为 w₁、w₂出现，我们只想用一个向量表示一个词，不管它出现在语境的哪个位置。于是，词嵌入矩阵 $E$ 的每一行表示一个词，每个向量的维度为 $d$，那么矩阵的维度就是 $V\times d$ 。

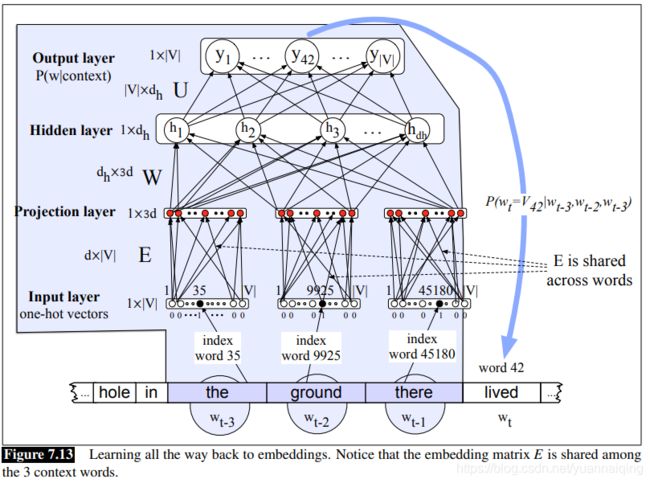
我们来看一下上图的过程：

1. 从 E 中查询三个词的嵌入向量：给定三个上文词语，查到他们的索引，创建 3 个 one-hot 向量，然后分别与 $E$ 相乘。词汇表中的一个词 x_i ，它的词嵌入为 $E{x}_i=e_i$，然后我们再把这三个词嵌入拼接起来作为上文词语，组成 投射层
2. 与 W 相乘：我们现在与 W 相乘（还要加上 b），通过使用非线性激活函数，送入到隐藏层 h。
3. 与 U 相乘：隐藏层 h 再与 矩阵 U 相乘。
4. 使用 softmax：使用 softmax 之后，输出层的每一个节点 i 都估测一个概率 $P=(w_t=i|w_{t-1},w_{t-2},w_{t-3})$

总的来看，如果我们用 e 来表示投射层，也就是 3 个词嵌入拼接形成的层，神经语言模型的公式就是：
$$e=(E{x}_1,E{x}_2,...,E{x}_3)$$$$h=\sigma (We+b)$$$$z=Uh$$$$y=softmax(z)$$

7.5.2 训练神经网络模型

训练这个模型，也就是设定好所有的参数 $\theta =E,W,U,b$，我们使用梯度下降，计算图中的误差反向传播的方法计算梯度。因此训练的过程中，不仅可以设置好网络中的 W 和 U，还能在预测后词的过程中学习到词嵌入矩阵 E 。
通常，训练会把非常长的文本作为输入，将所有句子连接起来，随机设置权重，然后迭代地遍历文本预测每一 w_t 。每一个词 w_t，它的交叉熵损失为(负对数似然估计)：$$L=-logp(w_t|w_{t-1},...,w_{t-n+1})$$这个损失函数的梯度为：
$${\theta }_{t+1}={\theta }_t-\eta \frac{\partial -logp(w_t|w_{t-1},...,w_{t-n+1})}{\partial \theta }$$这个梯度可以使用任何一个标准的神经网络框架，使用反向传播经过$U,W,b,E$求得。

7.6 总结

• 神经网络由神经单元构成，思想来源于人类的神经元，不过现在是一种抽象的计算机制。
• 每一个神经单元使输入值与权重向量相乘，加上偏置项，然后再通过一个非线性的激活函数，比如 sigmoid，tanh等。
• 在全连接的前馈网络中，i 层的每一个神经单元都与 i+1 层的全部神经单元相连，而且没有回路。
• 神经网络的强大在于早期层能够学习到表示，然后被后面的层用到。
• 神经网络是通过像梯度下降等优化算法进行训练。
• 误差反向传播，按照计算图进行反向求导，用来计算神经网络损失函数的梯度。
• 神经语言模型使用神经网络作为概率分类器，通过给定上文 的n 个词语，预测下一个词的概率。
• 神经语言模型可以使用预训练的词嵌入，也可以在语言建模过程中从头开始学习词嵌入。

文献和历史说明

神经网络起源于1940年代的 McCulloch-Pitts 神经元，是一个人类神经元的简化计算模型，可以使用命题逻辑来描述。50年代末60年代初，很多实验室开始研究神经网络；这个时期感知机得到了发展(Rosenblatt, 1958)，阈值转变为偏置。?
在人们发现一个感知机单元不能解决简单的XOR问题后（Minsky&Papert，1969），神经网络开始衰退。不过此后的二十年仍然有少量的工作在继续。一直到1980年代迎来复兴，得益于像反向传播等实用工具在构建更深网络的传播(Rumelhart, 1986)。在80年代，各种各样的神经网络和相关架构被发明，尤其是在心理学、认知科学中的应用，连接主义者或者并行分布处理等术语常被提及。这个时期发展出的一些原则和技术为现在的工作打下了基础，包括分布式表示（Hinto，1986），循环网络（Elman，1990），使用 tensor 进行组合(Smolensky, 1990)。
在1990年代，大型神经网络开始应用于很多实际的语言处理任务，比如手写字识别（LeCun，1989），语音识别（Morgan，1989）。2000年代初，计算机硬件的提升加上训练和优化技术的发展，使训练大型深度网络称为可能，出现了深度学习这一术语（Hinton，2006）。
关于这个主题有很多优秀的书籍，Goldberg (2017)全面介绍了神经网络在自然语言处理中的应用。想要全面了解神经网络，看Goodfellow（2016）和Nielsen（2015）。