多智能体强化学习入门

参考文章：万字长文：详解多智能体强化学习的基础和应用 、多智能体强化学习入门（一）——基础知识与博弈

推荐文章：多智能体强化学习路线图 (MARL Roadmap)

推荐综述论文：An Overview of Multi-Agent Reinforcement Learning from Game Theoretical Perspective

参考书籍：《深度强化学习学科前沿与实战应用》

多智能体强化学习（Multi-agent RL简称MARL），是由RL和多智能体系统结合而成的新领域。多智能体系统起源于分布式人工智能，分布式人工智能的研究目标是创建描述自然和社会系统的精确概念模型，研究内容是分布式问题求解（Distributed Problem Solving,DPS）和多智能体系统，核心是把系统分成若干智能，自治的子系统，它们在物理和地理上可以分散，可以独立执行任务，同时又可以相互通信，相互协调，共同完成任务，因此，和传统的人工智能研究相比，多智能体系统不仅考虑个体的智能程度，更多的是整个系统的自主性，社会性等。多智能体环境下具有代表性的算法是OpenAI研究团队提出的MADDPG，在后面会有专门的讲解。

目前的工作主要关注以下两方面的研究：

• 稳定性，要求系统能收敛到均衡态，因此所有的智能体策略都要收敛到协调平衡的状态，最常用的是Nash均衡。
• 适应性。要求当其它智能体改变策略是，系统的表现保持不变或者更加优异，在一般情况下适应性由定义的目标最优、兼容性或者安全性等形式表达。

简介

MARL是指一组具有自我控制能力、能够相互作用的智能体，在同一环境下通过感知器、执行器操作，进而形成完全合作性、完全竞争性或者混合类型的多智能体系统，每个多智能体的奖励都会受到其他智能体动作的影响。因此，如何学习一种策略使得系统达到均衡稳态是该多智能体系统的目标。

纳什均衡

在矩阵博弈中，如果联结策略$({\pi }_1^{\ast },...,{\pi }_n^{\ast })$满足
$$V_i({\pi }_1^{\ast },...,{\pi }_i^{\ast },{\pi }_n^{\ast })\ge V_i({\pi }_1,...,{\pi }_i,{\pi }_n),\forall {\pi }_i\in {\Pi }_i,i=1,...,n$$
则为一个纳什均衡。总体来说，纳什均衡就是一个所有智能体的联结策略。在纳什均衡处，对于所有智能体而言都不能在仅改变自身策略的情况下，来获得更大的奖励。

完全合作型

完全合作性的MARL系统中，认为系统的最大奖励需要智能体的相互协调才能获得，但当每个智能体都不清楚其他人选择的动作的情况下，得到的奖励都存在不确定性，会造成整个系统的收敛困难和随机性。相反在已知其他智能体的选择的前提下 ，智能体很容易就能学习到最高的奖励。

完全竞争型

完全竞争型的MARL中，一般采用最大最小化原则，即无论对方采取任何行动，智能体本身总是采取使自己受益最大的动作，最优策略就是无论对手如何选择，双方都应选择竞争，这样双方获得的奖励加起来才能实现最大化。

混合类型

这种类型的RL一般针对静态任务，直接对每个智能体应用单智能体的RL算法，不需要了解其他智能体的动作，所以各自更新独立的Q函数。如果甲乙需要处理AB两个文件，显然同时处理不同的文件能够节省时间，当甲乙做各自的更新表时，双方同时处理一个文件的奖励为0，但处理在各自的Q值表中，自己处理B文件自己得到的奖励是最高的。

---

马尔科夫博弈

在单智能体中RL可以用MDP来描述，而MARL需要马尔科夫博弈来描述，又称随机博弈（stochastic game）。包含两个概念，首先是多智能体系统的状态符合马尔科夫性，即下一个状态只与向前时刻有关，与前面的时刻无关。第二，博弈描述的是多智能体之间的关系。

马尔科夫博弈描述了多智能体系统，这里定义一个元组：
$$(N,S,a_1,a_2,...,a_N,T,\gamma ,r_1,...,r_N)$$
其中N是智能体个数，S是系统状态，一般是多智能体的联合状态，例如合一是所有智能体的坐标。$a_1,a_2,...,a_N$为智能体的动作集合，T为状态转移函数。$T：S\ast a_1\ast ...\ast a_N\ast S$。

$r_i(s,a_1,...,a_N,s^{\prime })$表示智能体在s状态时执行联合动作后再状态s’得到的奖励$r_i$，当每个智能体奖励函数一致时，智能体之间是合作关系，奖励函数相反时，智能体之间是竞争关系。奖励函数介于两者直接是混合关系。

---

优势与挑战

多智能体学习的优势是可以通过不同智能体之间共享经验，从而更快、更好地完成任务。当一个智能体出现故障时，其他智能体可以代替执行任务，提高系统的鲁棒性。当系统需要提高扩展性时，可以随时引入新的智能体。

同时MARL面临的挑战是随着状态、动作和智能体数目的增加，系统的计算复杂度也指数增长，并且难以定义学习目标，无法做到单独最大化某个智能体的奖励。其次，系统难以收敛到一个最优解。所有的智能体都是在一个不断变化的环节中同时学习，最后的策略会随着其他智能体策略的改变而改变，最后导致探索过程更加复杂。因此探索过程不能只满足获取环境信息，还需要其他智能体的信息，以此相互适应，但有不能过度探索，否则会打破整个系统的平衡，影响其他智能体的策略学习。

部分可见马尔科夫决策过程（POMDP）

在马尔科夫决策过程（简称MDP）中，一个重要前提是智能体对环境的观察是完整的，而现实中的智能体往往只能观察到部分信息，比如很多情况下难以获取系统的精确状态，另外就是智能体的传感器只能覆盖整个环境的一小部分。针对上述问题，部分可见马尔科夫决策过程（简称POMDP）这个更接近现实世界的模型被提出，这可以看作MDP的扩展。

通常，我们采用一个七元组$(S,A,T,R,O,Z,\gamma )$来描述POMDP，其中S、A、T、R、γ和MDP的定义一致。另外有：

O：一组观察结果集，比如机器人传感器获得的环境信息，在MDP中由于完全了解系统状态，O=S，在POMDP中观察仅在概率上取决于潜在的环境信息，因为在不同的环境状态中可以得到相同的观察，因此确定智能体所处的状态变得困难。

Z：$S\ast A\to \Delta (O)$是一个观察函数，表明系统状态和观察值之间的关系，具体是在智能体在执行动作a进入环境状态s’后得到观察者的概率。
$$Z(s^{\prime },a,o^{\prime })=P_r(O^{t+1}=o^{\prime }|S^{t+1}=s^{\prime },A^t=a)$$
现在整体一下流程：在时刻t，环境处于状态s，智能体采取动作a，根据状态转移方程$T(s^{\prime }|s,a)$进入环境状态s’，同时智能体获得观察值o，这取决于概率$Z(o’|s’,a) $，最后智能体得到奖励$r = r(s,a)$，目标是使智能体在每个时间步选择的动作能够最大化未来的折扣奖励。

---

在POMDP中，智能体不能确信自己所处的状态，因此决策的基础是当前所处状态的概率。智能体需要得到观测值来更新自己对当前所处状态的可信度，“信息收集”的动作可以让智能体先运动到邻近的位置，这个位置收集的信息可能加大智能体对自己所处状态的可信度。虽然无法得知状态，但是可以通过观察和动作的历史来决策，t时刻的观察和动作的历史定义为：
$$h_t=(a_0,o_1,...,o_{t-1},a_{t-1},o_t)$$
为了采用较短的历史代替所有的观察和行为，引入了信念状态$b(s)$的概念，表示对当前所处状态的可信度。
$$b_t(s)=P_r(s|h_t)$$
Sondik证明$b_t(s)$是对历史$h_t$的充分估计，在所有状态上维护一个概率分布与维护一个完整历史提供同样的信息。这样就能转化为基于信念空间状态的马尔科夫链来求解，因此POMDP问题的求解转化为求解信念状态函数和策略问题。

• 信念状态函数$B(s)：O\ast A\ast B(s)\to B(s)$
• 策略π：$B(s)\to A$

随着信念空间的引入，POMDP问题就可以看成是Belief MDP问题。寻求一种最优策略将当前信念状态隐射到智能体的动作上，根据当前信念状态和行为就可以决定下一周期的信念状态和行为。Belief MDP通常被描述为四元组$<B,A,T^b,r^b>$，具体如下：

• $B：B=\Delta (S)$是一系列连续的状态空间
• A：动作空间，和POMDP的定义一致。
• $T_b：B\ast A\to B$，状态转移函数，推导如下：

$$\begin{gathered} T_b(b,a,b^{\prime })=P_r(b^{\prime }|b,a)=\sum _{o\in O}{P}_r(b^{\prime }|a,b,o)P_r(o|a,b) \\ =\sum _{o\in O}{P}_r(b^{\prime }|a,b,o)\sum _{s^{\prime }\in S}Z(s^{\prime },a,o)\sum _{s\in S}T(s,a,s^{\prime })b(s) \end{gathered}$$

$$P_r(b^{\prime }|a,b,o)=\{\begin{array}{l}1,b_o^a=b^{\prime }\\ 0,b_o^a\ne b^{\prime }\end{array}\text{\hspace{1em}(1)}$$

信念度的更新可以表示为：
$$b_o^a(s^{\prime })=\frac{Z(s^{\prime },a,o){\sum }_{s\in S}T(s,a,s^{\prime })b(s)}{P_r(o|a,b)}$$
之后POMDP的最优策略的选择和值函数的构建可以类似普通的MDP决策进行，在Belief MDP下，一般定义值函数为
$$V_{t+1}(b)=\underset{a\in A}{\max }[r^b(b,a)+\gamma \sum _{b^{\prime }\in B}{T}^b(b,a,b^{\prime })V_t(b^{\prime })]$$
根据原始POMDP，有：
$$V_{t+1}(b)=\underset{a\in A}{\max }[\sum _{s\in S}b(s)r(s,a)+\gamma \sum _{o\in O}{P}_r(o|a,b)V_t(b_o^a)]$$

$$P_r(o|a,b)=\sum _{s^{\prime }\in S}Z(s^{\prime },a,o)\sum _{s\in S}T(s^{\prime }|s,a)b(s)$$

$${\pi }_{t+1}(b)=argma{x}_{a\in A}[\sum _{s\in S}b(s)r(s,a)+\gamma \sum _{o\in O}{P}_r(o|a,b)V_t(b_o^a)]$$

---

目前对POMDP算法的研究主要分为精确算法和近似算法，两者都使用了基于信念状态的模型，表示系统实际处于每个状态的概率。

由于POMDP模型可以更加真实反映客观世界的模型，对环境，动作和观察的不确定性有进行良好的建模，POMDP被应用到机器人路径规划、机器人导航、用户兴趣获取、对话系统等领域，这些领域要求尽量避免人体直接接触，需要依靠机器人进行操作，而在放射性废物回收，深海探矿、管道网络的检修和维护也非常符合POMDP模型。

在智能体面临行动产生结果的不确定性和实际状态的不确定性是，可以使用POMDP，例如最小化机器使用费用，最大化生产能力，道路检测管理，电网出现故障需要快速找到故障并排除，还可以应用到医疗诊断的问题上，通过病人的病症确定治疗方案。在军事领域，应用有移动目标的查找、跟踪、拯救，目标的辨认、武器的使用和分配等。

---

基于值函数的多智能体强化学习

1. 基于DQN

在多智能体协作的问题和研究中，相对主流的方法是2016年提出的CommNet和DLAL（RIAL），基于两者发展出的最新方法是2017年提出的BiCNet，它在个体行为上使用了DDPG代替DQN，群体链接中采用了双向循环网络取代单向网络。

2.增强智能体间学习

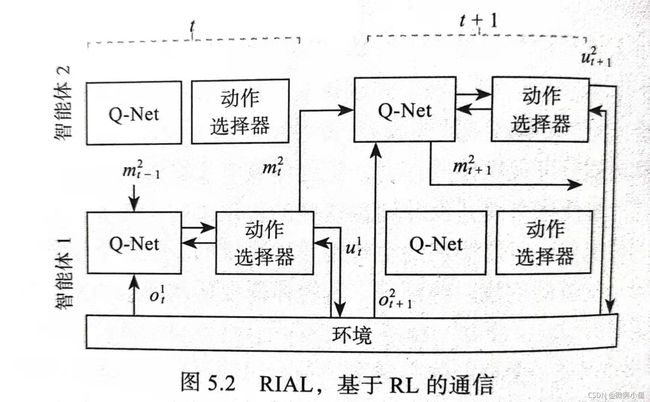
增强智能体间学习（Reinforced Inter-Agent Learning，RIAL）首先提出一组需要通信的多智能体，然后为这些智能体指定环境参数和学习算法，最后分析智能体如何学习通信协议。所有智能体有共同目标，虽然没有智能体可以观察底层的马尔科夫状态，但是每个智能体都接收到于该状态相关的观察，因此RIAL所考虑的任务是完全合作的，部分可观察的，顺序的多智能体决策问题，因此必须学习通信协议，学习时带宽不受限制。在执行过程中，智能体只能通过有限带宽的通道进行通信。

RIAL使用的是DRQN（Deep Recurrent Q-Network）解决部分可观测问题。它不是用前馈网络近似$Q(s,a)$，而是使用一个递归神经网络近似$Q(o,a)$，这样可以保持内部的状态并随时间累积观测值。，可以添加一个额外的输入$h_{t-1}$代表网络的隐藏状态，产生$Q(o_t,h_{t-1},a)$。

当多个智能体和部分可观察性共存时，智能体就有了交流的动机，在没有预先给出协议的情况下，智能体必须开发并同意这样的协议解决问题，协议是从行为观察历史到消息序列的映射，智能体还需要协调信息的发送和解释，这是非常困难的。

我们定义在RLAL中，每个智能体的Q网络表示为
$$Q^i(o_t^i,v_{t-1}^{i^{\prime }},h_{t-1}^i,a^i)$$
$h_{t-1}^i$和$o_t^i$是每个智能体的个体隐藏状态和换成，i是智能体的索引。

RIAL将网络分成$Q_a^i$和$Q_m^i$分别是环境动作和通信动作的Q值，动作选择器使用ε-greedy策略分别从动作网络中选择$a_t^i$和$m_t^i$，因此网络有|U|+|M|种输出。

$Q_a^i$和$Q_m^i$都使用DQN进行训练，但不使用经验复用池，以解释多个智能体并发学习时出现的额非平稳性，应为它会使经验过时并具有误导性。为了考虑部分可观测性，将智能体采取的动作a和m作为下一个时间步的输入。

如果智能体之间共享参数，变可以拓展RIAL为集中学习的网络，此变体只学习一个网络，所有智能体都使用这个网络。但智能体仍然可以表现不同，因为它们接收不同的观察结果，从而演变出不同的隐藏状态，此外每个智能体都接收自己的索引a作为输入从而进行个体化。参数共享大大减少了需要学习的参数量，从而加快了学习速度，在参数共享下，智能体学习两个Q函数$Q_a(o_t^i,m_{t-1}^{i^{\prime }},h_{t-1}^{t^{\prime }},a_{t-1}^i,m_{t-1}^i,i,a_t^i)$和$Q_m(.)$，对应动作a和信息m。$a_{t-1}^i$和$m_{t-1}^i$是上一个动作的输入，$m_{t-1}^{t^{\prime }}$是其他智能体的信息。

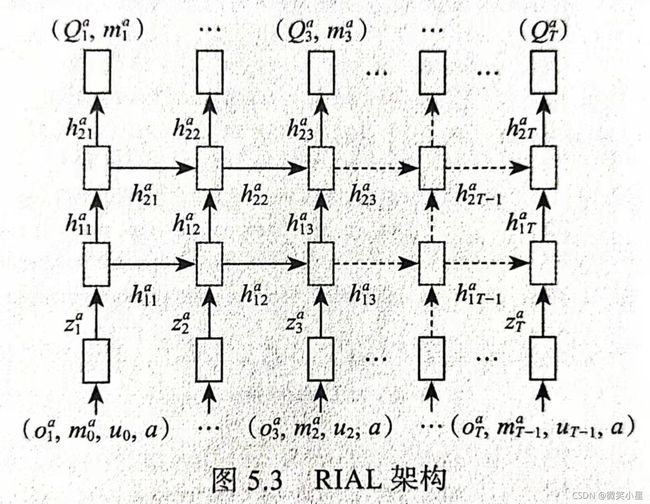
在不考虑参数共享的情况下，每个智能体包含一个RNN,RIAL将其为T时间步长张开，包括一个内部状态h、一个用于产生任务输出z的输入网络，以及一个用于Q值的输出网络和信息m。智能体i的输入被定义为$(o_t^i,m_{t-1}^{i^{\prime }},a_{t-1}^i,i)$的元组，输入i和$a_{t-1}^i$通过表传递，$m_{t-1}^{i^{\prime }}$通过一个一层MLP，两者都产生大小为128的输出，$o_t^i$通过任务特定网络处理，产生相同大小的附加输出。通过这些元素求和产生状态输出，具体如下：

$$z_t^i=(TaskMLP(o_t^i)+MLP[|M|,128](m_{t-1})+Lookup(a_{t-1}^i)+Lookup(i))$$

同时一个BN层用于预处理$m_{t-1}$时，网络性能和稳定性可以处理更好。通过具有GRU的2层RNN处理$z_t^i$,$h_{1,t}^i=GRU[128,128](z_t^i,h_{1,t-1}^i)$，其用于近似智能体的动作观察历史。最后顶部GRU层的输出$h_{2,t}^i$，是通过2层MLP $Q_t^i$，$m_t^i=MLP[128,128,(|U|+|M|)](h_{2,t}^i)$。

class SeitchCNet(nn.Module):
    def __init__(self,opt):
        self.opt = opt
        dropout_rate = opt.model_rnn_dropout_rate or 0
        self.rnn = nn.GRU(input_size = opt.model_rnn_size,
                          hidden_size = opt.model_rnn_size,
                          num_layers = opt.model_rnn_layers,
                          dropout = dropout_rate,
                         batch_first = True)
        self.outputs = nn.Sequential()
        if dropout_rate > 0:
            self.outputs.add_module('dropout1',nn.Dropout(dropout_rate))
        self.outputs.add_module('linear1',nn.Linear(opt.model_rnn_size,opt.model_rnn_size))
        if opt.model_bn:
            self.outputs.add_module('batchnorml',nn.BatchNormld(opt.model_rnn_size))
        self.outputs.add_module('relu1',nn.ReLU(inplace = True))
        self.outputs.add_module('linear2',nn.Linear(opt.model_rnn_size,opt.game_action_space_total))    
        
        def forward(self,o_t,messages,hidden,prev_action,agent_index):
            opt = self.opt
            o_t = Variable(o_t)
            hidden = Variable(o_t)
            prev_message = None
            if opt.model_dial:
                if opt.model_action_aware:
                    prev_action = Variable(prev_action)
            else:
                if opt.model_action_aware:
                    prev_action , prev_message = prev_action
                    prev_action = Variable(prev_message)
                    prev_message = Variable(prev_message)
                messages = Variable(messages)
            agent_index = Variable(agent_index)
            
            z_a, z_o, z_u, z_m = [0] * 4
            z_a = self.agent_lookup(agent_index)
            z_o = self.state_lookup(o_t)
            if opt.model_action_aware:
                z_u = self.prev_action_lookup(prev_action)
                if prev_message is not None:
                    z_u += self.prev_message_lookup(prev_message)
            z_m = self.messages_mlp(messages.view(-1,self.comm_size))
            
            z = z_a + z_o + z_u + z_m
            z = z.unsqueeze(1)
            
            rnn_out, h_out = self.rnn(z,hidden)
            outputs = self.outputs(rnn_out[:,-1,:].squeeze())
            
            return h_out, outputs

3.协同多智能体学习的价值分解网络

论文：Value-Decomposition Networks For Cooperative Multi-Agent Learning

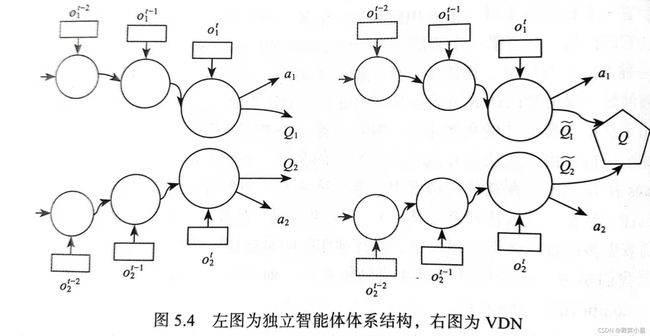
协同多智能体学习的价值分解网络（Value-Decomposition Networks,VDN），目的是从团队奖励中学习一个最优的线性价值分解，通过代表单个分量价值函数的深度神经网络对总Q梯度进行反向传播。这种附加价值分解是为了避免独立智能体出现虚假奖励。每个智能体学习的隐式值函数值依赖于局部的观察，因此更容易学习。

在原先的DQN多智能体基础上，VDN添加了增强功能，左图显示了随着时间的推移，本地观察如何进入两个智能体的网络（如图中所示的三个步骤），通过低线性层进循环层，然后产生单独的Q值。右图的网络说明了价值分解的主要贡献，VDN产生单独的“值”，它们相加到用于训练的联合Q函数，而动作则独立于各个输出而产生。

VDN假设联合价值函数可以分解为智能体的价值函数：
$$Q((h^1,h^2,...,h^N),(a^1,a^2,...a^N))\approx \sum _{i=1}^N\tilde{Q}(h^i,a^i)$$
其中$\tilde{Q}$只依赖于每个智能体的本地观察，通过求和从Q-learning规则中使用联合奖励反向传播来学习$\tilde{Q}$，即它是隐式学习的，而不是特定于智能体i的任何奖励中学习的，并且不强制$\tilde{Q}$是任何特定奖励的行为价值函数。定义：
$$\begin{gathered} Q^{\pi }(s,a)=E[\sum _{t-1}^{\infty }{\gamma }^{t-1}r(s_t,a_t)|s_t=s,a_1=a;\pi ] \\ =E[\sum _{t-1}^{\infty }{\gamma }^{t-1}{r}_1(o_t^1,a_t^1)|s_t=s,a_1=a;\pi ]+E[\sum _{t-1}^{\infty }{\gamma }^{t-1}{r}_2(o_t^2,a_t^2)|s_t=s,a_1=a;\pi ] \\ ={\bar{Q}}_1^{\pi }(s,a)+{\bar{Q}}_1^{\pi }(s,a) \end{gathered}$$
如果$(o^1,a^1)$不足以完全建模${\bar{Q}}_1^{\pi }(s,a)$，则智能体1可以将来自历史观察的信息储存在LSTM中，或者从通信信道中的智能体2接收信息，VDN可以做出预测：
$$Q^{\pi }(s,a)={\bar{Q}}_1^{\pi }(s,a)+{\bar{Q}}_2^{\pi }(s,a)={\tilde{Q}}_1^{\pi }(h^1,a^1)+{\tilde{Q}}_2^{\pi }(h^2,a^2)$$
可能的或VDN结构鼓励将此分解成更简单的功能。

VDN是将复杂的学习问题自动分解为更容易学习的局部子问题的一个步骤。此方法可以与权重共享和信息通道很好地结合在一起，从而是智能体能够始终最优地解决新的测试挑战，在再来的工作中，VDN有希望继续探讨基于非线性值聚合的价值分解研究。

4.多智能体强化学习的稳定经验复用池

论文原文：Stabilising Experience Replay for Deep Multi-Agent Reinforcement Learning

如何协调经验复用池于IQL的关系正在成为将深度MARL扩展到更复杂任务的关键障碍。MARL稳定经验复用池包含两种方法：一是将复用池中的经验定义为非环境数据。通过使用该元组中的联合动作的概率来增强复用池中的每条经验，根据当时使用的策略，稍后元组被采样用于训练时，可以计算采样权重校正。旧数据倾向于较低的重要性权重，因此该方法会自然衰减数据。二是通过让每个智能体学习一种策略来避免IQL的非稳定性。受hyper Q-learning的启发，该策略根据观察其行为推断出的其他智。能体策略的估计。具体是每个智能体值需要满足一个低维指纹的条件，该指纹足以消除复用池中采样经验原则位置的歧义。

5. 单调值函数分解（QMIX）

QMIX: Monotonic Value Function Factorisation for Deep Multi-Agent Reinforcement Learning

MARL中如何表示和使用动作价值函数使得系统达到一个均衡稳态是多智能体系统的目标。

IQL让每个智能体单独定义一个函数$Q_a$。这种方法不能明确表示智能体之间的相互作用，并且可能不会收敛，因为每个智能体的学习都被其他智能体的探索和学习混淆。

另一种是学习一个完全集中式的动作价值函数，即反事实多智能体（counterfactual Multi-Agent COMA）,用它来指导actor-critic框架中的分布策略的优化，但需要on-policy学习，导致样本效率低下，并且存在多个智能体是，训练完全集中的critic是不切实际的。

因此这里采用了QMIX，和VDN一样采用集中式分解Q的方法，处于IQL和COMA之间，但可以表示更丰富的动作价值函数。由于VDN的完全因子分解对于获得分散策略并不是必须的。相反，QMIX只需要确保在Q上执行的全局argmax与在每个Q上执行的一组单独的argmax参数产生相同的结果。因此，只需要求对$Q^{\pi }$于每个$Q_a$之间存在单调约束，即：
$$\frac{\delta Q^{\pi }}{\delta Q_a}\ge 0$$
不同于VDN简单的总和，QMIX有代表每个$Q_a$的智能体网络和将它们组合到$Q^{\pi }$中的混合网络组成，以复杂的非线性方式确保集中式和分散式策略之间的一致性。同时，它通过限制混合网络具有正权重来强制执行上式的约束，因此QMIX可以表示复杂的集中式动作价值函数，可以很好扩展智能体数量，并允许通过线性时间的argmax操作轻松得到分散策略。

6.深度强化学习中的对立智能体建模（DRON）

论文原文：Opponent Modeling in Deep Reinforcement Learning

在一些协作或竞争的任务环境中工作的智能体，需要预测其他智能体行为并快速做出决策，对立智能体建模（DRON）的目标是在RL环境中建立一个通用的对手建模框架，是智能体能够利用各种对手的特质。

DRON在对手的策略中模拟不确定性，而不是将其分类为一组固定组合。DRON根据过去的观察来学习对手的隐藏表示，并使用隐藏表示来计算自适应响应。此外DRON还提出两种体系结构，一种使用简单级联来组合这两种模块，另一种使用基于混合专家网络（mixture-of-expert network）的体系结构。虽然DRON隐含地对对手进行建模，但可以通过多任务处理增加额外的监督，例如采取动作或策略。

7.平均场多智能体强化学习

均值场理论论文：Phase transitions and critical phenomena

平均场Q学习论文：Mean Field Multi-Agent Reinforcement Learning

当大量智能体共存时会由于维度的增大和智能体的交互的指数增长，学习变得困难，联合学习也会带来Nash均衡问题。

现在考虑每个智能体都能于一组其他智能体进行交互，通过一系列直接交互，任何一对智能体对在全局范围内相互联系。可以使用均质场理论（mean field theory）来解决可扩展性，即智能体群中的相互作用近似于使用来自某个整体智能体的平均效应和单个智能体的相互作用。所以，学习是在两个实体之间而不是许多实体直接相互增强：单个智能体的最优策略的学习基于智能体的数目动态，同时根据个体策略更新动态数目，基于这样的想法，提出平均场Q学习（mean field Q-learning）和平均场actor-critic算法。该算法分析了解决方案对Nash均衡的收敛性，并且在资源分配、伊辛模型估计（Ising model estimation）和战斗游戏方面的实验证明了平均场方法的学习效果。

---

基于策略的多智能体强化学习

1.基于自身策略的其他智能体行为预测（SOM）

论文：Modeling Others using Oneself in Multi-Agent Reinforcement Learning

2.双重平均方案（PD-DistlAG）

论文：Multi-Agent Reinforcement Learning via Double Averaging Primal-Dual Optimization

3.多智能体深度强化学习的统一博弈论方法（PRSO）

论文： A Unified Game-Theoretic Approach to Multi-agent Reinforcement Learning

基于AC框架的多智能体强化学习

1. 多智能体深度确定性策略梯度（MADDPG）

论文：Multi-Agent Actor-Critic for Mixed Cooperative-Competitive Environments

2.多智能体集中规划的价值函数策略梯度（Dec-POMDP）

论文：Policy Gradient With Value Function Approximation For Collective Multiagent Planning

3.多智能体系统的策略表示学习

论文：Learning Policy Representations in Multiagent Systems

4.部分可观察环境下的多智能体策略优化

论文：Actor-Critic Policy Optimization in Partially Observable Multiagent Environments

5. 基于联网智能体的完全去中心化MARL

论文：Fully Decentralized Multi-Agent Reinforcement Learning with Networked Agents