多智能体强化学习
传统RL算法面临的一个主要问题是由于每个智能体都是在不断学习改进其策略,因此从每一个智能体的角度看,环境是一个动态不稳定的,这不符合传统RL收敛条件。并且在一定程度上,无法通过仅仅改变智能体自身的策略来适应动态不稳定的环境。由于环境的不稳定,将无法直接使用之前的经验回放等DQN的关键技巧。policy gradient算法会由于智能体数量的变多使得本就有的方差大的问题加剧。
1.强化学习和多智能体强化学习
我们知道,强化学习的核心思想是“试错”(trial-and-error):智能体通过与环境的交互,根据获得的反馈信息迭代地优化。在 RL 领域,待解决的问题通常被描述为马尔科夫决策过程。
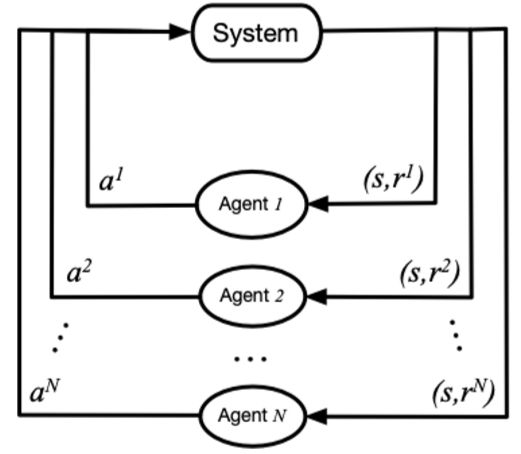
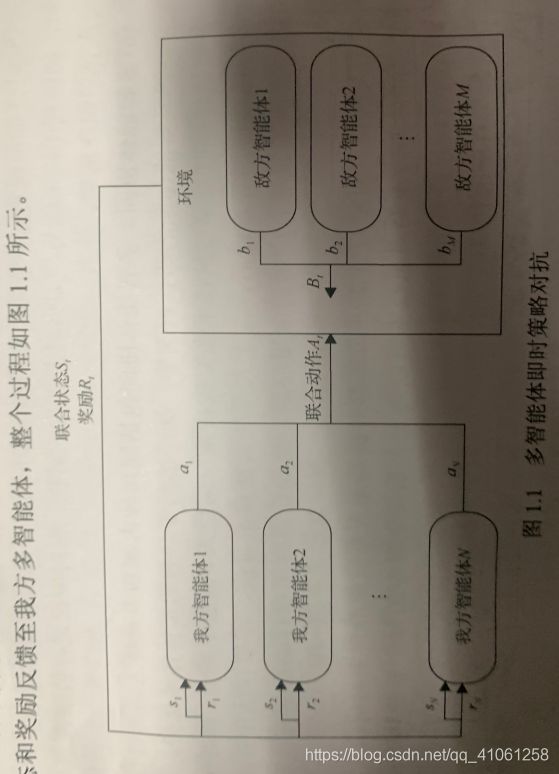
当同时存在多个智能体与环境交互时,整个系统就变成一个多智能体系统(multi-agent system)。每个智能体仍然是遵循着强化学习的目标,也就是是最大化能够获得的累积回报,而此时环境全局状态的改变就和所有智能体的联合动作(joint action)相关了。因此在智能体策略学习的过程中,需要考虑联合动作的影响。
环境状态空间:全局状态,局部状态
动作空间:(离散动作,连续动作)同构智能体,异构智能体
奖励函数:全局奖励,局部奖励
注:一般情况下,状态,动作整体考虑,例如单个智能体的Q,V值
面临的问题
1.信息不完全,整体对于全局的环境信息把握不够准确,某个智能体局部信息把握不够准确。
2.动作搜索空间大
3.即时对抗性
4.环境不够稳定,因为自己执行动作,其他智能体也在执行动作
基础知识:
纳什均衡
在马尔科夫博弈中,所有智能体根据当前的环境状态(或者是观测值)来同时选择并执行各自的动作,该各自动作带来的联合动作影响了环境状态的转移和更新,并决定了智能体获得的奖励反馈。它可以通过元组 < S,A1,…,An,T,R1,…,Rn > 来表示,其中 S 表示状态集合,Ai 和 Ri 分别表示智能体 i 的动作集合和奖励集合,T 表示环境状态转移概率,表示损失因子。此时,某个智能体 i 获得的累积奖励的期望可以表示为:
对于马尔科夫博弈,**纳什均衡(Nash equilibrium)**是一个很重要的概念,它是在多个智能体中达成的一个不动点,对于其中任意一个智能体来说,无法通过采取其他的策略来获得更高的累积回报,在数学形式上可以表达为:
在该式中,π^{i,}表示智能体 i 的纳什均衡策略。
2.多智能体强化学习方法
1。对于多智能体强化学习问题,一种直接的解决思路:将单智能体强化学习方法直接套用在多智能体系统中,即每个智能体把其他智能体都当做环境中的因素,仍然按照单智能体学习的方式、通过与环境的交互来更新策略;这是 independent Q-learning 方法的思想。这种学习方式固然简单也很容易实现,但忽略了其他智能体也具备决策的能力、所有个体的动作共同影响环境的状态,使得它很难稳定地学习并达到良好的效果。
- 智能体之间是完全竞争关系
minimax Q-learning 算法用于两个智能体之间是完全竞争关系的零和随机博弈。首先是最优值函数的定义:对于智能体 i,它需要考虑在其他智能体(i-)采取的动作(a-)令自己(i)回报最差(min)的情况下,能够获得的最大(max)期望回报。该回报可以表示为:
在式子中,V 和 Q 省略了智能体 i 的下标,是因为在零和博弈中设定了 Q1=-Q2,所以上式对于另一个智能体来说是对称等价的。这个值函数表明,当前智能体在考虑了对手策略的情况下使用贪心选择。这种方式使得智能体容易收敛到纳什均衡策略。
在学习过程中,基于强化学习中的 Q-learning 方法,minimax Q-learning 利用上述 minimax 思想定义的值函数、通过迭代更新 Q 值;动作的选择,则是通过线性规划来求解当前阶段状态 s 对应的纳什均衡策略。
minimax Q 方法是竞争式博弈中很经典的一种思想,基于该种思想衍生出很多其他方法,包括 Friend-or-Foe Q-learning、correlated Q-learning,以及接下来将要提到的 Nash Q-learning。
3 智能体之间是半合作半竞争(混合)关系
- Nash Q-learning
双人零和博弈的更一般形式为多人一般和博弈(general-sum game),此时 minimax Q-learning 方法可扩展为 Nash Q-learning 方法。当每个智能体采用普通的 Q 学习方法,并且都采取贪心的方式、即最大化各自的 Q 值时,这样的方法容易收敛到纳什均衡策略。Nash Q-learning 方法可用于处理以纳什均衡为解的多智能体学习问题。它的目标是通过寻找每一个状态的纳什均衡点,从而在学习过程中基于纳什均衡策略来更新 Q 值。
具体地,对于一个智能体 i 来说,它的 Nash Q 值定义为:
![]()
此时,假设了所有智能体从下一时刻开始都采取纳什均衡策略,纳什策略可以通过二次规划(仅考虑离散的动作空间,π是各动作的概率分布)来求解。
在 Q 值的迭代更新过程中,使用 Nash Q 值来更新:
可以看到,对于单个智能体 i,在使用 Nash Q 值进行更新时,它除了需要知道全局状态 s 和其他智能体的动作 a 以外,还需要知道其他所有智能体在下一状态对应的纳什均衡策略π。进一步地,当前智能体就需要知道其他智能体的 Q(s’)值,这通常是根据观察到的其他智能体的奖励和动作来猜想和计算。所以,Nash Q-learning 方法对智能体能够获取的其他智能体的信息(包括动作、奖励等)具有较强的假设,在复杂的真实问题中一般不满足这样严格的条件,方法的适用范围受限。
- Friend-or-Foe-Q
该算法假设智能体可以分成两类,分别是智能体i的朋友和智能体i的敌人,智能体i的朋友共同合作使得i的奖励最大化,智能体i的敌人共同合作使得i的奖励最小化。
- WoLF-PHC
该算法是PHC算法的扩展,用于处理一般和随机博弈。WoLF算法是当智能体做得比期望值好时小心缓慢地调整参数,当智能体做得比期望值差时,加快步伐调整参数。
4 智能体之间是完全合作关系;
前面提到的智能体之间的两种关系,都涉及到了个体和个体的相互竞争,所以对于个体来说,在策略学习过程中考虑对方(更一般地,其他智能体)的决策行为,才能够做出更好地应对动作,这是比较容易理解的。那么,如果智能体之间完全是合作关系,个体的决策也要考虑其他智能体的决策情况吗?实际上,“合作”意味着多个智能体要共同完成一个目标任务,即这个目标的达成与各个体行为组合得到的联合行为相关;如果个体“一意孤行”,那么它很难配合其他队友来共同获得好的回报。所以,智能体的策略学习仍然需要考虑联合动作效应,要考虑其他具有决策能力的智能体的影响。
两个问题,第一个信用分配问题,第二个智能体协作问题。
怎样实现在智能体策略学习过程中考虑其他协作智能体的影响呢?这个问题我们可以分类讨论,分类的依据是具体问题对于智能体协作的条件要求,即智能体通过协作获得最优回报时,是否需要协调机制:
- 不需要协作机制
对于一个问题(或者是任务),当所有智能体的联合最优动作是唯一的时候,完成该任务是不需要协作机制的。这个很容易理解,假设对于环境中的所有智能体 {A,B} 存在不只一个最优联合动作,即有 {πA,πB} 和{hA,hB},那么 A 和 B 之间就需要协商机制,决定是同时取π,还是同时取 h;因为如果其中一个取π、另一个取 h,得到的联合动作就不一定是最优的了。
Team Q-learning 是一种适用于不需要协作机制的问题的学习方法,它提出对于单个智能体 i,可以通过下面这个式子来求出它的最优动作 hi:
Distributed Q-learning 也是一种适用于不需要协作机制的问题的学习方法,不同于 Team Q-learning 在选取个体最优动作的时候需要知道其他智能体的动作,在该方法中智能体维护的是只依据自身动作所对应的 Q 值和一个本地策略 ,从而得到个体最优动作。
- 隐式的协作机制
在智能体之间需要相互协商、从而达成最优的联合动作的问题中,个体之间的相互建模,能够为智能体的决策提供潜在的协调机制。
在联合动作学习(joint action learner,JAL)方法中,智能体 i 会基于观察到的其他智能体 j 的历史动作、对其他智能体 j 的策略进行建模。
在频率最大 Q 值(frequency maximum Q-value, FMQ)[7]方法中,在个体 Q 值的定义中引入了个体动作所在的联合动作取得最优回报的频率,从而在学习过程中引导智能体选择能够取得最优回报的联合动作中的自身动作,那么所有智能体的最优动作组合被选择的概率也会更高。
JAL 和 FMQ 方法的基本思路都是基于均衡求解法,但这类方法通常只能处理小规模(即智能体的数量较少)的多智能体问题:在现实问题中,会涉及到大量智能体之间的交互和相互影响,而一般的均衡求解法受限于计算效率和计算复杂度、很难处理复杂的情况。在大规模多智能体学习问题中,考虑群体联合动作的效应,包括当前智能体受到的影响以及在群体中发挥的作用,对于智能体的策略学习是有较大帮助的。
3.多智能体双向协调网络
状态:全局状态,局部状态
动作:三维(攻击,机动)方向 距离
奖励 全局 局部
网络结构 双向RNN,作为智能体间的通信通道,还可以作为本地的记忆器,使得智能体保持其内部状态的同时与其他智能体共享信息
4.反事实多智能体策略梯度
COMA策略梯度三个主要思想
1.采用集中式Critic训练,也就是采用同一个Critic网络集中训练,充分利用全局信息,稳定地学习。
分布式执行,每个智能体根据自己的局部观察来进行决策
2.采用反事实基线来进行信用分配,也就是比较多智能体联合动作的全局奖励,与将智能体采取的动作替换成默认动作后联合动作的全局奖励之间的差距
3.使用Critic网络来有效估计反事实基线
5.MADDPG
- 集中式训练,分布式执行:训练时采用集中式学习训练critic与actor,使用时actor只用知道局部信息就能运行。critic需要其他智能体的策略信息,本文给了一种估计其他智能体策略的方法,能够只用知道其他智能体的观测与动作。
- 改进了经验回放记录的数据。为了能够适用于动态环境。
- 利用策略集合效果优化(policy ensemble):对每个智能体学习多个策略,改进时利用所有策略的整体效果进行优化。以提高算法的稳定性以及鲁棒性。
MADDPG集中式的学习,分布式的应用。因此我们允许使用一些额外的信息(全局信息)进行学习,只要在应用的时候使用局部信息进行决策就行。这点就是Q-learning的一个不足之处,Q-learning在学习与应用时必须采用相同的信息。所以这里MADDPG对传统的AC算法进行了一个改进,Critic扩展为可以利用其他智能体的策略进行学习,这点的进一步改进就是每个智能体对其他智能体的策略进行一个函数逼近。
6.QMIX
1.学习得到分布式策略。
- 本质是一个值函数逼近算法。
- 由于对一个联合动作-状态只有一个总奖励值,而不是每个智能体得到一个自己的奖励值,因此只能用于合作环境,而不能用于竞争对抗环境。
- QMIX算法采用集中式学习,分布式执行应用的框架。通过集中式的信息学习,得到每个智能体的分布式策略。
- 训练时借用全局状态信息来提高算法效果。是后文提到的VDN方法的改进。
- 接上一条,QMIX设计一个神经网络来整合每个智能体的局部值函数而得到联合动作值函数,VDN是直接求和。
- 每个智能体的局部值函数只需要自己的局部观测,因此整个系统在执行时是一个分布式的,通过局部值函数,选出累积期望奖励最大的动作执行。
- 算法使联合动作值函数与每个局部值函数的单调性相同,因此对局部值函数取最大动作也就是使联合动作值函数最大。
。 - 接上一条,QMIX设计一个神经网络来整合每个智能体的局部值函数而得到联合动作值函数,VDN是直接求和。
- 每个智能体的局部值函数只需要自己的局部观测,因此整个系统在执行时是一个分布式的,通过局部值函数,选出累积期望奖励最大的动作执行。
- 算法使联合动作值函数与每个局部值函数的单调性相同,因此对局部值函数取最大动作也就是使联合动作值函数最大。
- 算法针对的模型是一个分布式多智能体部分可观马尔可夫决策过程(Dec-POMDP)。