多智能体强化学习（三）单智能体强化学习

通过试验和错误，一个RL智能体试图找到最佳的策略，以最大化其长期回报。该过程由马尔可夫决策过程表示。

1. 问题制定：马尔可夫决策过程

定义1（马尔可夫决策过程）一个MDP可以用一个由关键元素$<\mathbb{S}、\mathbb{A}、P、R、\gamma >$组成的元组来描述。

• $\mathbb{S}:$ 一组环境状态。
• $\mathbb{A}:$ 智能体可能执行的操作的集合。
• $\mathbb{P}：\mathbb{S}\times \mathbb{A}\to ∆(\mathbb{S}):$对于每个时间步骤t∈N，给定代理的动作为∈A，从状态$s_{\in }\mathbb{S}$到状态在下一个时间步骤$s^{\prime }\in \mathbb{S}$中的转换概率。
• $R：\mathbb{S}\times \mathbb{A}\times \mathbb{S}\to \mathbb{R}：$奖励函数，返回从s到s’的标量值。奖励的绝对值一致受$R_{max}$为界。
• $\gamma \in [0,1]$ 是表示时间值的折扣系数。

在每个时间步长t中，环境都有一个状态$s_t$。智能体观察此状态，并在上执行操作。该操作使环境转换到下一个状态$s_{t+1}\sim P(\cdot |s_t，a_t)$，新环境立即返回奖励$R(s_t，a_t，s_{t+1})$。奖励功能也可以写成$R：\mathbb{S}\times \mathbb{A}\to \mathbb{R}$，可与$R：\mathbb{S}\times \mathbb{A}\times \mathbb{S}\to \mathbb{R}$互换(参见VanOtterlo和Wiering（2012)，第10页）。智能体的目标是解决MDP：找到使奖励随时间最大化的最优政策。数学上，一个共同的目标是让智能体找到一个马尔可夫变量（即，输入只取决于当前状态)和平稳的(即，函数形式是与时间无关的）策略函数$\pi ：\mathbb{S}\to ∆(\mathbb{A})$，使用∆（·）表示概率单形，它可引导其采取顺序行动，从而使折扣的累计奖励最大化：

MDP的另一个常见的数学目标是最大化时间平均奖励：
我们在这项工作中没有考虑到这些，并参考马哈德万（1996）来全面分析时间平均回报的目标。

基于等式的目标函数（1），在给定的策略π下，我们可以将状态动作函数(即q函数，它决定执行状态a的预期返回)和值函数（它确定与状态策略相关的返回）定义为：

其中${\mathbb{E}}^{\pi }$是无限长状态动作轨迹$\tau =(s_0,a_0,s_1,a_1,\dots )$的概率测度${\mathbb{P}}^{\pi }$下的期望，其中${\mathbb{P}}^{\pi }$由状态转换概率P、策略π、初始状态s和初始动作a(在q函数的情况下)诱导。Q-函数与值函数之间的连接是

2. 奖励最大化的理由

由等式（1）给出的RL的当前模型认为，单个奖励函数的期望值足以解决我们希望“智能代理”能够解决的任何问题。这一想法的理由深根于冯诺伊曼-摩根斯坦(VNM)实用理论（冯诺伊曼和摩根斯坦，2007）。这个理论本质上证明了一个智能体是VNM有理的，当且仅当存在一个实值效用（或，奖励）函数，这样代理的每一个偏好都是通过最大化单一的期望奖励来描述的。VNM效用定理是著名的预期效用理论的基础（舒梅克，2013年），该理论本质上指出，理性可以被建模为最大化一个期望值。具体地说，VNM效用定理提供了预期效用假设成立的充要条件。换句话说，理性相当于VNM-理性，可以肯定的假设在任何复杂的场景中，智能实体将始终选择具有最高预期效用的动作。

诚然，在真正的决策者在实践中违反关于理性的一些假设之前，人们就被接受了（吉格伦泽和塞尔滕，2002年）。事实上，这些条件更多地被认为是理性决策的“公理”。在多目标MDP的情况下，我们仍然能够通过两个时间尺度过程通过标度函数将多个目标转换为单目标MDP；我们参考Roijers等人。（2013）以了解更多细节。

3. 解决马尔可夫决策过程

MDPs中常用的一个概念是（折扣-正常化）占用度量${\mu }^{\pi }(s，a)$，它唯一对应于给定的策略$\pi$，反之亦然(Syed等人，2008，定理2)，定义为

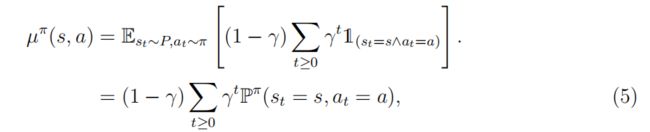
其中，$1$是一个指示器功能。请注意，在等式中（5），P是状态转移概率，${\mathbb{P}}^{\pi }$是遵循平稳策略π时特定状态-动作对的概率。${\mu }^{\pi }(s，a)$的物理意义是一种概率测度量，它计算对单个可接受的状态动作对的预期折扣访问次数。相应地，${\mu }^{\pi }(s)=\sum {\mu }^{\pi }(s，a)$是折扣状态探视频率，即由π引起的马尔可夫过程的平稳分布。通过占用措施，我们可以写出等式（4）作为

的内部乘积。这意味着求解一个MDP可以被看作是求解一个包含
的线性程序(LP)，然后最优策略是

然而，这种解决MDP的方法仍然在教科书水平，旨在提供理论见解，但在具有数百万变量的大规模LP中实际上缺乏（帕帕迪米里和特西西克利斯，1987）。当MDP的状态动作空间连续时，LP配方也不能帮助解决。

在最优控制的背景下(Bertsekas，2005)，动态规划策略，如策略迭代和值迭代，也可以应用于求解能够最大化等式的最优策略（3）&等式（4），但这些方法需要了解模型的确切形式：转换函数$P(\cdot |s,a)$和奖励函数$R(s、a、s^{\prime })$。

另一方面，在RL的设置中，代理在与环境的交互过程中通过反复试验过程学习最优策略，而不是使用模型的先验知识。“学习”一词本质上意味着代理将其在交互过程中获得的经验转化为关于环境模型的知识。基于求解目标、最优策略或最优值函数，RL算法可以分为两种类型：基于值的方法和基于策略的方法。

3.1 基于价值的方法

对于所有具有有限状态和动作的MDPs，至少存在一个确定性平稳最优策略(萨顿和Barto，1998；Szepesv´ari，2010)。引入了基于值的方法来寻找最大化等式(3)的最优q函数$Q^{\ast }$。相应地，通过采取${\pi }^{\ast }=argma{x}_a{Q}^{\ast }(s，a)$的贪婪作用，可以从q函数中得到最优策略。经典的Q-学习算法(Watkins和Dayan，1992)近似于$\hat{Q}的Q^{\ast }$，并通过时差学习更新其价值(Sutton，1988)。

理论上，给定了贝尔曼最优性算子$H^{\ast }$，定义为

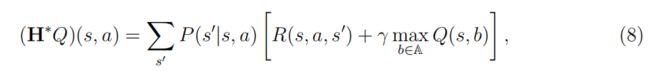
我们知道它是一个收缩映射，最优的Q-函数是唯一的不动点，即$H^{\ast }(Q^{\ast })=Q^{\ast }$。q-学习算法提取了等式中$(s、a、R、s^{\prime })$的随机样本（7）至接近等式（8），但在状态动作集是离散的和有限的，并且被无限次访问的假设下，仍然保证收敛到最优Q函数(Szepesv´ari和Littman，1999)。Munos和Szepesv´ari（2008）通过推导出具有有限数量样本的无限状态空间的高概率误差界，将收敛结果扩展到一个更现实的设置。

最近，Mnih等人。（2015）应用神经网络作为更新等式的q函数的函数逼近器(7).具体来说，DQN优化了以下方程式：

神经网络参数θ通过绘图进行拟合。从重放缓冲区$D$中的样本，然后以监督学习的方式更新。$Q_{\theta }-$是一个缓慢更新的目标网络，可以帮助稳定训练。杨等人研究了DQN的收敛性和有限样本分析。(2019c)。

3.2 基于策略的方法

基于策略的方法被设计为直接搜索策略空间，以找到最优策略π∗。您可以参数化策略表达式${\pi }^{\ast }\approx {\pi }_{\theta }（\cdot |s）$，并沿着使累积奖励$\theta \leftarrow \theta +\alpha {\nabla }_{\theta }{V}^{{\pi }_{\theta }}(s)$最大化的方向更新参数θ，以找到最优策略。然而，梯度将取决于政策变化对状态分布的未知影响。著名的策略梯度(PG)定理（Sutton等人，2000）推导出一个不涉及状态分布的解析解，即：

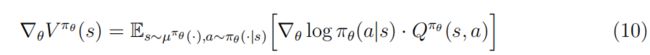
其中，${\mu }^{{\pi }_{\theta }}$是策略πθ下的状态占用度量，$\nabla log{\pi }_{\theta }(a|s）$是策略的更新分数。当策略是确定性的且动作集是连续的时，我们得到确定性策略梯度(DPG)定理（Silver等人，2014）作为


图4：交叉点示例中的随机时间的快照。这个场景被抽象为有两辆车，每辆车都采取两种可能的行动之一：让路或冲。每个联合动作对的结果都用一个正常形式的游戏来表示，行玩家的奖励值用红色表示，列玩家的奖励值用黑色表示。该博弈的纳什均衡(NE)为（收益率、收益率）和（收益率、收益率）。如果两辆车自私地不考虑自己的奖励最大化，他们最终会发生事故。

PG定理的一个经典实现是 REINFORCE（威廉姆斯，1992），它使用一个样本返回$R_t={\sum }_{i=t}^T{\gamma }^{i-t}{r}_i$来估计$Q^{{\pi }_{\theta }}$。或者，我们可以使用Qω模型（也称为批评者）来近似真实的$Q^{{\pi }_{\theta }}$，并通过TD学习更新参数ω。这种方法产生了著名的演员-评论家的方法(Konda和Tsitsiklis，2000年；彼得斯和沙尔，2008年)。演员-评论家方法的重要变体包括信任区域方法（Schulman等人，2015、2017）、具有最优基线的PG（Weaver和Tao，2001；Zhao等人，2011）、软演员-评论家方法（Haarnoja等人，2018，）和深度确定性政策梯度(DDPG)方法（米勒克拉普等人，2015）。