第十二届蓝桥杯 2021年省赛真题 (Java 大学C组) 第一场

---

回家吧，回到最初的美好

挂上来先睡了，这几天随便写写

---

#A ASC

本题总分：5 分

---

问题描述

已知大写字母 $A$ 的 $ASCII$ 码为 $65$，请问大写字母 $L$ 的 $ASCII$ 码是多少？

---

答案提交

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

---

76

calcCode：

public class Test {
     

    public static void main(String[] args) {
     
        System.out.println((int)'L');
    }
}

?这是什么新型攻击性言论

---

#B 空间

本题总分：5 分

---

问题描述

小蓝准备用 256MB 的内存空间开一个数组，数组的每个元素都是 32 位二进制整数，如果不考虑程序占用的空间和维护内存需要的辅助空间，请问256MB 的空间可以存储多少个 32 位二进制整数？

---

答案提交

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

---

67108864 || 8388608

calcCode：

public class Test {
     

    public static void main(String[] args) {
     
        System.out.println(256 << 18);
    }
}

256 * 1024 * 1024 / 4 换成位运算就是 256 << 10 + 10 - 2

但其实是可以解释成 兆比特(Mbit) ，而不是字面上的 兆字节(MByte)。
换句话说 1MB = 8Mb，也就是可以在这个答案上再除个8。

但出现这个想法主要还是不同的学习路线之间 Byte 和 bit 太过混乱
再解释就太长篇大论了，也就说虽然你是对的，但你也没错
老谜语人了

---

#C 卡片

本题总分：10 分

---

问题描述

小蓝有很多数字卡片，每张卡片上都是数字 0 到 9。
小蓝准备用这些卡片来拼一些数，他想从 1 开始拼出正整数，每拼一个，就保存起来，卡片就不能用来拼其它数了。
小蓝想知道自己能从 1 拼到多少。
例如，当小蓝有 30 张卡片，其中 0 到 9 各 3 张，则小蓝可以拼出 1 到 10，但是拼 11 时卡片 1 已经只有一张了，不够拼出 11。
现在小蓝手里有 0 到 9 的卡片各 2021 张，共 20210 张，请问小蓝可以从 1拼到多少？
提示：建议使用计算机编程解决问题。

---

答案提交

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

---

3181

calcCode：

public class Test {
     

    public static void main(String[] args) {
     
        int ans = 1, figure[] = new int[10];
        flag: for (int i = 1; ; i = ++ans) {
     
            do if (figure[i % 10]++ == 2021) break flag;
            while ((i /= 10) > 0);
        }
        System.out.println(ans - 1);
    }
}

---

#D 相乘

本题总分：10 分

---

问题描述

小蓝发现，他将 $1$ 至 $1000000007$ 之间的不同的数与 $2021$ 相乘后再求除以$1000000007$ 的余数，会得到不同的数。
小蓝想知道，能不能在 $1$ 至 $1000000007$ 之间找到一个数，与 $2021$ 相乘后再除以$1000000007$ 后的余数为 $999999999$。如果存在，请在答案中提交这个数；
如果不存在，请在答案中提交 $0$。

---

答案提交

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

---

17812964

calcCode：

public class Test {
     

    public static void main(String[] args) {
     
        for (long i = 0; i < 2021; i++)
            if ((i * 1000000007 + 999999999) % 2021 == 0)
                System.out.println((i * 1000000007 + 999999999) / 2021);
    }
}

可以正着求，4小时内肯定是能跑完的

---

#E 路径

本题总分：15 分

---

问题描述

小蓝学习了最短路径之后特别高兴，他定义了一个特别的图，希望找到图中的最短路径。
小蓝的图由 $2021$ 个结点组成，依次编号 $1$ 至 $2021$。
对于两个不同的结点 $a,b$，如果 $a$ 和 $b$ 的差的绝对值大于 $21$，则两个结点之间没有边相连；如果 $a$ 和 $b$ 的差的绝对值小于等于 $21$，则两个点之间有一条长度为 $a$ 和 $b$ 的最小公倍数的无向边相连。
例如：结点 $1$ 和结点 $23$ 之间没有边相连；结点 $3$ 和结点 $24$ 之间有一条无向边，长度为 $24$；结点 $15$ 和结点 $25$ 之间有一条无向边，长度为 $75$。
请计算，结点 $1$ 和结点 $2021$ 之间的最短路径长度是多少。
提示：建议使用计算机编程解决问题。

---

答案提交

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

---

10266837

calcCode：

public class Main {
     

    static final int n = 2021;

    public static void main(String[] args) {
     
        int[][] floyd = new int[n][n];
        for (int i = 0; i < n; i++)
            for (int j = i + 1; j < n && j < i + 22; j++)
                floyd[i][j] = floyd[j][i] = lcm(i + 1, j + 1);
        for (int k = 0; k < n; k++)
            for (int i = 0; i < n; i++)
                for (int j = 0; j < n; j++)
                    if (floyd[i][k] != 0 &&  floyd[k][j] != 0&& (floyd[i][j] == 0 || floyd[i][k] + floyd[k][j] < floyd[i][j])) floyd[i][j] = floyd[i][k] + floyd[k][j];
        System.out.println(floyd[0][n - 1]);
    }

    static int gcd(int a, int b) {
      return b == 0 ? a : gcd(b, a % b); }

    static int lcm(int a, int b) {
      return a * b / gcd(a, b); }
}

Floyd yyds

重写时发现这题无向图的条件是没有实际意义的
因为最优结果必然是从节点序列大小来看的单向

import java.util.Arrays;

public class Main {
     

    public static void main(String[] args) {
     
        int[] path = new int[2022];
        Arrays.fill(path, 0x3F3F3F3F);
        path[1] = 0;
        for (int i = 2; i <= 2021; i++)
            for (int j = i - 1; j > 0 && j >= i - 21; j--)
                if (path[i] > lcm(i, j) + path[j]) path[i] = lcm(i, j) + path[j];
        System.out.println(path[2021]);
    }

    static int gcd(int a, int b) {
      return b == 0 ? a : gcd(b, a % b); }

    static int lcm(int a, int b) {
      return a * b / gcd(a, b); }
}

虽然今年这场我没去打(后些年也打不了了)
但有限的时间还是别放在这种乱写都能出结果的题上面

---

#F 时间显示

时间限制: 1.0s 内存限制: 512.0MB 本题总分: 15 分

---

问题描述

小蓝要和朋友合作开发一个时间显示的网站。在服务器上，朋友已经获取了当前的时间，用一个整数表示，值为从 $1970$ 年 $1$ 月 $1$ 日 $00:00:00$ 到当前时刻经过的毫秒数。
现在，小蓝要在客户端显示出这个时间。小蓝不用显示出年月日，只需要显示出时分秒即可，毫秒也不用显示，直接舍去即可。
给定一个用整数表示的时间，请将这个时间对应的时分秒输出。

---

输入格式

输入一行包含一个整数，表示时间。

---

输出格式

输出时分秒表示的当前时间，格式形如 $HH:MM:SS$，其中 $HH$ 表示时，值为 $0$ 到 $23$，$MM$ 表示分，值为 $0$ 到 $59$，$SS$ 表示秒，值为 $0$ 到 $59$。时、分、秒不足两位时补前导 0。

---

测试样例₁

Input：
46800999

Output：
13:00:00

测试样例₂

Input：
1618708103123

Output：
01:08:23

---

评测用例规模与约定

对于所有评测用例，给定的时间为不超过 $10^{18}$ 的正整数。

---

code：

import java.time.LocalTime;
import java.util.Scanner;

public class Main {
     

    public static void main(String[] args) {
     
        System.out.println(LocalTime.MIN.plusSeconds(new Scanner(System.in).nextLong() / 1000).format(java.time.format.DateTimeFormatter.ISO_LOCAL_TIME));
    }
}

虽然是送分题
但怕有人看不清我出招顺序

import java.time.format.DateTimeFormatter;
import java.time.LocalTime;
import java.util.Scanner;

public class Main {
     

    public static void main(String[] args) {
     
        Scanner in = new Scanner(System.in);
        long k = in.nextLong();
        LocalTime time = LocalTime.MIN.plusSeconds(k / 1000);
        DateTimeFormatter format = DateTimeFormatter.ISO_LOCAL_TIME;
        System.out.println(time.format(format));
    }
}

---

#G 最少砝码

时间限制: 1.0s 内存限制: 512.0MB 本题总分：20 分

---

问题描述

你有一架天平。现在你要设计一套砝码，使得利用这些砝码可以称出任意小于等于 $N$ 的正整数重量。
那么这套砝码最少需要包含多少个砝码？
注意砝码可以放在天平两边。

---

输入格式

输入包含一个正整数 $N$。

---

输出格式

输出一个整数代表答案。

---

测试样例₁

Input：
7

Output：
3

Explanation：
3 个砝码重量是 1、4、6，可以称出 1 至 7 的所有重量。
1 = 1；
2 = 6 − 4 (天平一边放 6，另一边放 4)；
3 = 4 − 1；
4 = 4；
5 = 6 − 1；
6 = 6；
7 = 1 + 6；
少于 3 个砝码不可能称出 1 至 7 的所有重量。

---

评测用例规模与约定

对于所有评测用例，$1\le N\le 1000000000$。

---

code：

import java.util.Scanner;

public class Main {
     

    public static void main(String[] args) {
     
        int n = new Scanner(System.in).nextInt(), ans = 1;
        for (long i = 1, k = 1; i < n; i += k *= 3, ans++);
        System.out.println(ans);
    }
}

1: [1 - 1] = 1
2: [1 - 4] + 3
3: [1 - 13] + 9
4: [1 - 40] + 27
......

有一说一，规律题就是纯纯的恶心人

---

#H 杨辉三角形

时间限制: 5.0s 内存限制: 512.0MB 本题总分：20 分

---

问题描述

下面的图形是著名的杨辉三角形：

如果我们按从上到下、从左到右的顺序把所有数排成一列，可以得到如下数列：
$1,1,1,1,2,1,1,3,3,1,1,4,6,4,1,...$
给定一个正整数 $N$，请你输出数列中第一次出现 $N$ 是在第几个数？

---

输入格式

输入一个整数 $N$。

---

输出格式

输出一个整数代表答案。

---

测试样例₁

Input：
6

Output：
13

---

评测用例规模与约定

对于 $20$% 的评测用例，$1\le N\le 10$；
对于所有评测用例，$1\le N\le 1000000000$。

---

code：

20就爱要不要了，只能说不会

---

#I 左孩子右兄弟

时间限制: 2.0s 内存限制: 512.0MB 本题总分：25 分

---

问题描述

对于一棵多叉树，我们可以通过 “左孩子右兄弟” 表示法，将其转化成一棵二叉树。
如果我们认为每个结点的子结点是无序的，那么得到的二叉树可能不唯一。换句话说，每个结点可以选任意子结点作为左孩子，并按任意顺序连接右兄弟。
给定一棵包含 $N$ 个结点的多叉树，结点从 $1$ 至 $N$ 编号，其中 $1$ 号结点是根，每个结点的父结点的编号比自己的编号小。请你计算其通过 “左孩子右兄弟” 表示法转化成的二叉树，高度最高是多少。注：只有根结点这一个结点的树高度为 $0$ 。
例如如下的多叉树：

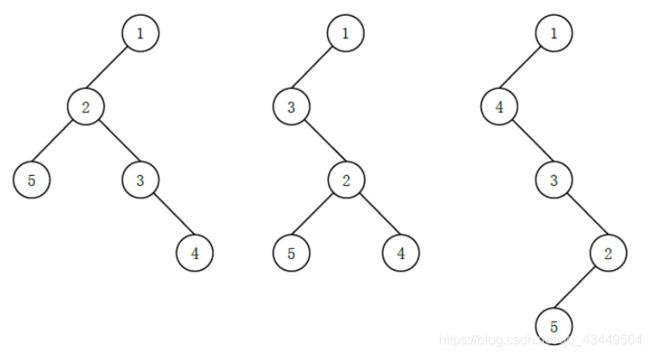
可能有以下 3 种 (这里只列出 3 种，并不是全部) 不同的 “左孩子右兄弟”表示：

其中最后一种高度最高，为 4。

---

输入格式

输入的第一行包含一个整数 $N$。
以下 $N-1$ 行，每行包含一个整数，依次表示 $2$ 至 $N$ 号结点的父结点编号。

---

输出格式

输出一个整数表示答案。

---

测试样例₁

Input：
5
1
1
1
2

Output：
4

---

评测用例规模与约定

对于 $30$% 的评测用例，$1\le N\le 20$；
对于所有评测用例，$1\le N\le 100000$。

---

code：

import java.io.IOException;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.*;

public class Main {
     

    static List<Integer>[] graph;
    static List leaf = Collections.EMPTY_LIST;

    public static void main(String[] args) throws IOException {
     
        BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
        int n = Integer.parseInt(in.readLine()), k = 0;
        Arrays.fill(graph = new List[n + 1], leaf);
        for (int i = 2; i <= n; i++) {
     
            k = Integer.parseInt(in.readLine());
            if (graph[k] == leaf)
                graph[k] = new ArrayList();
            graph[k].add(i);
        }
        System.out.println(dfs(1));
    }

    static int dfs(int node) {
     
        int max = 0;
        for (int k: graph[node])
            max = max(max, dfs(k));
        return graph[node].size() + max;
    }

    static int max(int a, int b) {
      return a > b ? a : b; }
}

题读懂了就好做了，深搜就行

因为对于一个节点的操作只有左连接一个子节点然后该节点右串连其余子节点

---

#J 双向排序

时间限制: 5.0s 内存限制: 512.0MB 本题总分: 25 分

---

问题描述

给定序列 $(a1,a2,\cdot \cdot \cdot ,an)=(1,2,\cdot \cdot \cdot ,n)$，即 $ai=i$。
小蓝将对这个序列进行 $m$ 次操作，每次可能是将 $a1,a2,\cdot \cdot \cdot ,aqi$ 降序排列，或者将 $aqi,aqi+1,\cdot \cdot \cdot ,an$ 升序排列。
请求出操作完成后的序列。

---

输入格式

输入的第一行包含两个整数 $n,m$，分别表示序列的长度和操作次数。
接下来 $m$ 行描述对序列的操作，其中第 $i$ 行包含两个整数 $p_i,q_i$ 表示操作类型和参数。当 $p_i=0$ 时，表示将 $a_1,a_2,\cdot \cdot \cdot ,a_{q_i}$ 降序排列；当 $p_i=1$ 时，表示将$a_{q_i},a_{q_i+1},\cdot \cdot \cdot ,a_n$ 升序排列。

---

输出格式

输出一行，包含 $n$ 个整数，相邻的整数之间使用一个空格分隔，表示操作完成后的序列。

---

测试样例₁

Input：
3 3
0 3
1 2
0 2

Output：
3 1 2

Explanation：
原数列为 (1, 2, 3)。
第 1 步后为 (3, 2, 1)。
第 2 步后为 (3, 1, 2)。
第 3 步后为 (3, 1, 2)。与第 2 步操作后相同，因为前两个数已经是降序了。

---

评测用例规模与约定

对于 $30$% 的评测用例，$n,m\le 1000$；
对于 $60$% 的评测用例，$n,m\le 5000$；
对于所有评测用例，$1\le n,m\le 100000$，$0\le a_i\le 1$，$1\le b_i\le n$。

---

code：

import java.io.*;
import java.util.Comparator;
import java.util.StringTokenizer;
import static java.util.Arrays.sort;

public class Main {
     

    public static void main(String[] args) {
     
        InputReader in = new InputReader(System.in);
        PrintWriter out = new PrintWriter(System.out);
        int n = in.nextInt(), m = in.nextInt(), p, q;
        Comparator comp = new Comparator<Integer>() {
     
            public int compare(Integer o1, Integer o2) {
      return o2 - o1; }
        };
        Integer a[] = new Integer[n + 1];
        for (int i = 1; i <= n; i++)
            a[i] = i;
        while (m-- > 0) {
     
            p = in.nextInt();
            q = in.nextInt();
            if (p == 1) sort(a, q, n + 1);
            else  sort(a, 1, q + 1, comp);
        }
        for (int i = 1; i <= n; i++) {
     
            out.print(a[i]);
            out.write(' ');
        }
        out.flush();
    }

    static class InputReader {
     

        BufferedReader read;
        StringTokenizer token;
        String delimiters;

        InputReader (InputStream in) {
      this(in, " \t\n\r\f"); }

        InputReader (InputStream in, String delimiters) {
     
            this.read = new BufferedReader(new InputStreamReader(in));
            this.token = new StringTokenizer("", this.delimiters = delimiters);
        }

        String next() {
     
            while (!token.hasMoreTokens())
                try {
     
                    token = new StringTokenizer(read.readLine(), delimiters);
                } catch (IOException e) {
     
                    e.printStackTrace();
                }
            return token.nextToken();
        }

        int nextInt() {
      return Integer.parseInt(next()); }
    }
}

60% 太小 API就能解决
后面 n、m 的大小又太暧昧了，60可以了

---