LeetCode刷题记录---广度优先搜索(BFS)算法
每次刷到广度优先搜索(BFS)算法题将在此博文更新~~~
广度优先搜索(BFS)类似于树的按层遍历,可以用队列实现。
其过程可以描述为:首先访问一个初始顶点,并将其标记为已访问过,接着访问其所有未被访问过的邻接点,其访问次序可以任意,并均标记为已访问过。然后在分别依次访问这些顶点的所有未被访问过的邻接点,并标记为已访问过。以此类推,直到图中所有和初始点有路径相通的顶点都被访问过。
先来介绍一下创建队列使用到的函数:
collections.deque()创建的队列是一个双端队列,可以从队列两端插入\移出元素。
import collections
d = collections.deque([])
d.append('a') # 在最右边添加一个元素,此时 d=deque('a')
d.appendleft('b') # 在最左边添加一个元素,此时 d=deque(['b', 'a'])
d.extend(['c','d']) # 在最右边添加所有元素,此时 d=deque(['b', 'a', 'c', 'd'])
d.extendleft(['e','f']) # 在最左边添加所有元素,此时 d=deque(['f', 'e', 'b', 'a', 'c', 'd'])
d.pop() # 将最右边的元素取出,返回 'd',此时 d=deque(['f', 'e', 'b', 'a', 'c'])
d.popleft() # 将最左边的元素取出,返回 'f',此时 d=deque(['e', 'b', 'a', 'c'])
d.rotate(-2) # 向左旋转两个位置(正数则向右旋转),此时 d=deque(['a', 'c', 'e', 'b'])
d.count('a') # 队列中'a'的个数,返回 1
d.remove('c') # 从队列中将'c'删除,此时 d=deque(['a', 'e', 'b'])
d.reverse() # 将队列倒序,此时 d=deque(['b', 'e', 'a'])
f=d.copy()
print(f)#deque(['b', 'e', 'a'])
f.clear()
print(f)#deque([])
#可以指定队列的长度,如果添加的元素超过指定长度,则原元素会被挤出。
e=collections.deque(maxlen=5)
e.extend([1,2,3,4,5])
e.append("a")
print(e)
#deque([2, 3, 4, 5, 'a'], maxlen=5)
e.appendleft("b")
print(e)
#deque(['b', 2, 3, 4, 5], maxlen=5)
e.extendleft(["c","d"])
print(e)
#deque(['d', 'c', 'b', 2, 3], maxlen=5)
再来讲下可能会使用到的collections.defaultdict()模块:
Python中通过Key访问字典,当Key不存在时,会引发‘KeyError’异常。为了避免这种情况的发生,可以使用collections.defaultdict()方法来为字典提供默认值。
key值可自定义,value的类型与collections.defaultdict()括号中设置类型的相同。
如:
import collections
s = [('yellow', 1), ('blue', 2), ('yellow', 3), ('blue', 4), ('red', 1)]
# defaultdict
d = collections.defaultdict(list) #括号内的参数可以指定类型
#collections.defaultdict(int):它为每个键生成的初始值为0
#如果要设置每个键的值为常数值1,则可以这样:collections.defaultdict(lambda: 1)
for k, v in s:
d[k].append(v) #就是这里和dict()不一样,用dict()的字典,这里会发生KeyError异常
print(d.items())
output:dict_items([(‘yellow’, [1, 3]), (‘blue’, [2, 4]), (‘red’, [1])])
其他功能和dict()一样。
| 难度 | 题目 |
|---|---|
| 简单 | 对称二叉树 |
| 简单 | 二叉树的最小深度 |
| 简单 | N叉树的最大深度 |
| 简单 | 员工的重要性 |
| 简单 | 二叉树的堂兄弟节点 |
| 中等 | 二叉树的层序遍历 |
| 中等 | 二叉树的层序遍历 II |
| 中等 | 二叉树的锯齿形层序遍历 |
| 中等 | 填充每个节点的下一个右侧节点指针 |
| 中等 | 被围绕的区域 |
| 中等 | 克隆图 |
| 中等 | 二叉树的右视图 |
| 中等 | 岛屿数量 |
| 中等 | 课程表 |
| 中等 | 课程表 II |
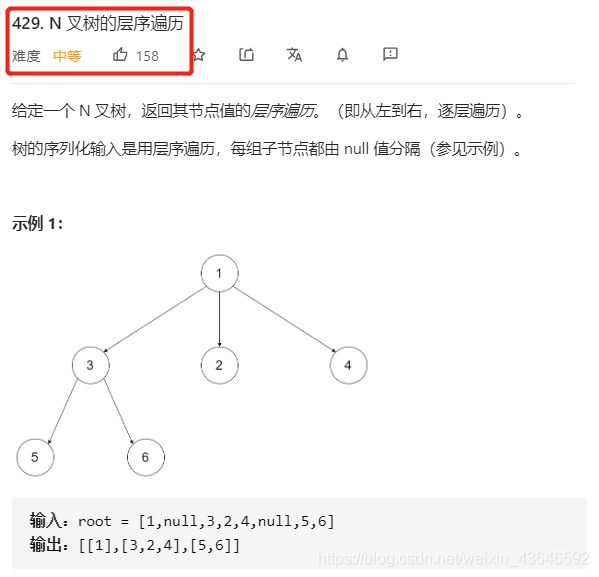
| 中等 | N叉树的层序遍历 |
| 中等 | 最小高度树 |
| 中等 | 找树左下角的值 |
| 中等 | 扫雷游戏 |
| 中等 | 完全平方数 |
| 中等 | 零钱兑换 |
⭐对称二叉树:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
import collections
class Solution:
def isSymmetric(self, root: TreeNode) -> bool:
if not root or not(root.left or root.right):
return True
queue = collections.deque([]) #创建一个队列
queue.append(root.left)
queue.append(root.right)
while queue:
left = queue.popleft()
right = queue.popleft()
if not (left or right): #两节点都为空,则继续循环
continue
if not (left and right): #两者有一个为空则返回False
return False
if left.val != right.val:
return False
queue.append(left.left)
queue.append(right.right)
queue.append(left.right)
queue.append(right.left)
return True
⭐二叉树的最小深度:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
import collections
class Solution:
def minDepth(self, root: TreeNode) -> int:
if not root:
return 0
queue = collections.deque([])
queue.append((root, 1))
while queue:
tempnode = queue[0][0]
level = queue[0][1]
queue.popleft()
if not (tempnode.left or tempnode.right):
return level
if tempnode.left:
queue.append((tempnode.left, level+1))
if tempnode.right:
queue.append((tempnode.right, level+1))
⭐N叉树的最大深度:
"""
# Definition for a Node.
class Node:
def __init__(self, val=None, children=None):
self.val = val
self.children = children
"""
import collections
class Solution:
def maxDepth(self, root: 'Node') -> int:
if not root:
return 0
queue = collections.deque()
queue.append((root, 1))
max_depth = 0
while queue:
tempnode = queue[0][0]
level = queue[0][1]
queue.popleft()
for n in tempnode.children: #遍历每个结点的所有孩子结点
queue.append((n, level+1))
max_depth = max(level, max_depth)
return max_depth
或者快一点不用比较max:
"""
# Definition for a Node.
class Node:
def __init__(self, val=None, children=None):
self.val = val
self.children = children
"""
import collections
class Solution:
def maxDepth(self, root: 'Node') -> int:
if not root:
return 0
queue = collections.deque()
queue.append((root, 1))
while queue:
root,depth=queue.popleft()
if root.children:
for node in root.children:
queue.append((node,depth+1))
return depth
⭐员工的重要性:

这题的关键是利用了哈希表将员工id(键)与员工类(值)对应了起来。
"""
# Definition for Employee.
class Employee:
def __init__(self, id: int, importance: int, subordinates: List[int]):
self.id = id
self.importance = importance
self.subordinates = subordinates
"""
import collections
class Solution:
def getImportance(self, employees: List['Employee'], id: int) -> int:
#创建哈希表保存,键对应员工id,值为员工类
id_map = dict()
for p in employees:
id_map[p.id] = p
if id not in id_map.keys():
return 0
queue = collections.deque()
queue.append(id_map[id])
sum_importance = 0
#将给定员工的下属一个个进队列,然后出列读出其重要度
while queue:
new_employee = queue.popleft()
sum_importance += new_employee.importance
for i in new_employee.subordinates:
queue.append(id_map[i])
return sum_importance
⭐二叉树的堂兄弟节点:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
import collections
class Solution:
def isCousins(self, root: TreeNode, x: int, y: int) -> bool:
if not root: return False
depth_x, depth_y = 0, 0
parent_x, parent_y = None, None
#保存节点和它的父节点
queue = collections.deque()
queue.append((root, None))
level = 0
while queue:
queue_len = len(queue)
level += 1
#用来控制每一层的遍历
for i in range(queue_len):
newnode = queue[0][0]
newparent = queue[0][1]
queue.popleft()
if newnode.val==x:
depth_x = level
parent_x = newparent
if newnode.val==y:
depth_y = level
parent_y = newparent
if newnode.left: queue.append((newnode.left, newnode))
if newnode.right: queue.append((newnode.right, newnode))
return depth_x==depth_y and parent_x!=parent_y
⭐二叉树的层序遍历:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
import collections
class Solution:
def levelOrder(self, root: TreeNode) -> List[List[int]]:
if not root: return []
queue = collections.deque()
queue.append(root)
result = []
while queue:
temp_list = []
queuelen = len(queue)
for i in range(queuelen):
newnode = queue.popleft()
temp_list.append(newnode.val)
if newnode.left: queue.append(newnode.left)
if newnode.right: queue.append(newnode.right)
result.append(temp_list)
return result
⭐二叉树的层序遍历 II:

这一题相比上一题(二叉树的层序遍历)不同的只是这题是从底向上输出层序遍历的结果,只需在最后的返回结果处修改为:return result[::-1] (索引含义:取出列表所有元素,按倒序)即可实现hhh:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
import collections
class Solution:
def levelOrderBottom(self, root: TreeNode) -> List[List[int]]:
if not root: return []
queue = collections.deque()
queue.append(root)
result = []
while queue:
temp_list = []
queuelen = len(queue)
for i in range(queuelen):
newnode = queue.popleft()
temp_list.append(newnode.val)
if newnode.left: queue.append(newnode.left)
if newnode.right: queue.append(newnode.right)
result.append(temp_list)
return result[::-1]
⭐二叉树的锯齿形层序遍历:

和前面的二叉树层序遍历差不多而已,这题只要加多个标志位控制层数为奇or偶数时是否倒序遍历即可实现:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def zigzagLevelOrder(self, root: TreeNode) -> List[List[int]]:
if not root: return []
queue = collections.deque()
queue.append(root)
result = []
flag = 0 #用来控制层数为奇or偶数时是否倒序遍历
while queue:
flag += 1
temp_list = []
queuelen = len(queue)
for i in range(queuelen):
newnode = queue.popleft()
temp_list.append(newnode.val)
if newnode.left: queue.append(newnode.left)
if newnode.right: queue.append(newnode.right)
if flag%2==1: result.append(temp_list)
elif flag%2==0: result.append(temp_list[::-1])
return result
⭐填充每个节点的下一个右侧节点指针:


这题关键就是在每一层的遍历时,在新节点出列后,用新节点的next指向队首元素:
"""
# Definition for a Node.
class Node:
def __init__(self, val: int = 0, left: 'Node' = None, right: 'Node' = None, next: 'Node' = None):
self.val = val
self.left = left
self.right = right
self.next = next
"""
import collections
class Solution:
def connect(self, root: 'Node') -> 'Node':
if not root: return root
queue = collections.deque()
queue.append(root)
while queue:
queuelen = len(queue)
for i in range(queuelen):
newnode = queue.popleft()
if i<queuelen-1:
newnode.next = queue[0]
if newnode.left: queue.append(newnode.left)
if newnode.right: queue.append(newnode.right)
return root
因为上面用到了队列存储每一层的节点,所以空间复杂度为O(N),又因为每个节点到会被访问一次所以时间复杂度为O(N)。
下面考虑空间复杂度为常量级O(1)的做法:
![]()
从下图看,无非两种连接方式:
node.left.next = node.rightnode.right.next = node.next.left

所以设计一个循环,通过当前层控制下一层节点的连接即可实现。
设置一个标志节点记录每一层的首节点,即当前层第一个节点的左孩子节点(不用队列)。再设置一个节点记录当前节点,方便每次循环将其右移。
"""
# Definition for a Node.
class Node:
def __init__(self, val: int = 0, left: 'Node' = None, right: 'Node' = None, next: 'Node' = None):
self.val = val
self.left = left
self.right = right
self.next = next
"""
import collections
class Solution:
def connect(self, root: 'Node') -> 'Node':
if not root: return root
mostleft = root
#控制所有层是否遍历处理完
while mostleft.left:
head = mostleft
#控制当前层是否遍历完
while head:
#情况1:
head.left.next = head.right
#情况2:
if head.next:
head.right.next = head.next.left
head = head.next #移动到当前层的下一节点
mostleft = mostleft.left #赋值为下一层的最左节点
return root
⭐被围绕的区域:

这题主要想法就是:除了与边界上为‘O’的直接相连的或间接相连的元素,那肯定就是被‘X’包围了呗。所以利用队列遍历将与边界上为‘O’的直接相连的或间接相连的元素做上标记,然后再重新遍历整个矩阵,处理掉被包围的即可:
import collections
class Solution:
def solve(self, board: List[List[str]]) -> None:
"""
这题主要想法就是:除了与边界上为‘O’的直接相连的或间接相连的元素,
那肯定就是被‘X’包围了呗。所以利用队列遍历将与边界上为‘O’的直接
相连的或间接相连的元素做上标记,然后再重新遍历整个矩阵,处理掉被包围的即可。
"""
if not board: return
#n:行,m:宽
n, m = len(board), len(board[0])
queue = collections.deque()
#遍历左右两边
for i in range(n):
if board[i][0] == "O": queue.append((i, 0))
if board[i][m - 1] == "O": queue.append((i, m - 1))
#遍历上下两边
for i in range(1, m - 1):
if board[0][i] == "O": queue.append((0, i))
if board[n - 1][i] == "O": queue.append((n - 1, i))
#将与边界上为‘O’的直接相连或间接相连的标记为‘*’
while queue:
x, y = queue.popleft()
board[x][y] = '*'
for tx,ty in [(x-1, y), (x+1, y), (x, y-1), (x, y+1)]:
if 0<=tx<n and 0<=ty<m and board[tx][ty]=='O':
queue.append((tx, ty))
for i in range(n):
for j in range(m):
if board[i][j]=='*': board[i][j]='O'
elif board[i][j]=='O': board[i][j]='X'
⭐克隆图:



因为是无向图,我们要遍历整个图的每个节点进行克隆。所以如果只用队列进行进列、出列来遍历图,不记录被访问过的节点,会进入死循环,如下图所示:

可以使用一个哈希表存储所有已被访问和克隆的节点。哈希表中的 key 是原始图中的节点,value 是克隆图中的对应节点。如果当前访问的节点不在哈希表中,则创建它的克隆节点并存储在哈希表中。
"""
# Definition for a Node.
class Node:
def __init__(self, val = 0, neighbors = None):
self.val = val
self.neighbors = neighbors if neighbors is not None else []
"""
import collections
class Solution:
def cloneGraph(self, node: 'Node') -> 'Node':
if not node: return node
visited = {
} #使用哈希表存储所有已被访问和克隆过的节点。键:原始图中的节点;值:克隆图中的节点
visited[node] = Node(node.val, [])
queue = collections.deque() #建立队列进行BFS
queue.append(node)
while queue:
newnode = queue.popleft()
for neighbor in newnode.neighbors:
if neighbor not in visited.keys():
visited[neighbor] = Node(neighbor.val, [])
queue.append(neighbor)
visited[newnode].neighbors.append(visited[neighbor]) #为当前节点添加邻居节点
return visited[node]
来个更简单的,直接调用内置库函数进行深拷贝哈哈哈哈(这样就没意思了兄dei):
"""
# Definition for a Node.
class Node:
def __init__(self, val = 0, neighbors = None):
self.val = val
self.neighbors = neighbors if neighbors is not None else []
"""
class Solution:
def cloneGraph(self, node: 'Node') -> 'Node':
import copy
return copy.deepcopy(node)
⭐二叉树的右视图:

就将二叉树的每一层的最右边节点的值加入result就OK,非常简单的一题:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
import collections
class Solution:
def rightSideView(self, root: TreeNode) -> List[int]:
if not root: return []
queue = collections.deque()
queue.append(root)
result = []
while queue:
queuelen = len(queue)
temp_list = []
for i in range(queuelen):
newnode = queue.popleft()
temp_list.append(newnode.val)
if newnode.left: queue.append(newnode.left)
if newnode.right: queue.append(newnode.right)
#就将二叉树的每一层的最右边节点的值加入result就OK,非常简单的一题
result.append(temp_list[-1])
return result
⭐岛屿数量:

遍历整个grid二维列表:若某位置为1,将其压入队列,开始BFS,直到队列为空,将BFS过程中为‘1’的位置置‘0’。
最终BFS的次数即为岛屿数量。
import collections
class Solution:
def numIslands(self, grid: List[List[str]]) -> int:
if not grid: return 0
nrow = len(grid)
ncolumn = len(grid[0])
queue = collections.deque()
num_result = 0
for r in range(nrow):
for c in range(ncolumn):
if grid[r][c] == '1':
grid[r][c] = '0'
queue.append((r, c))
num_result += 1 #岛屿数量加1
while queue:
x, y = queue.popleft()
for tx,ty in [(x-1,y), (x+1,y), (x,y-1), (x,y+1)]:
if 0<=tx<nrow and 0<=ty<ncolumn and grid[tx][ty] == '1':
grid[tx][ty] = '0'
queue.append((tx, ty))
return num_result
⭐课程表:


先来讲下下面会使用到的collections.defaultdict()模块:
Python中通过Key访问字典,当Key不存在时,会引发‘KeyError’异常。为了避免这种情况的发生,可以使用collections.defaultdict()方法来为字典提供默认值。
key值可自定义,value的类型与collections.defaultdict()括号中设置类型的相同。
如:
import collections
s = [('yellow', 1), ('blue', 2), ('yellow', 3), ('blue', 4), ('red', 1)]
# defaultdict
d = collections.defaultdict(list)
for k, v in s:
d[k].append(v) #就是这里和dict()不一样,用dict()的字典,这里会发生KeyError异常
print(d.items())
output:dict_items([(‘yellow’, [1, 3]), (‘blue’, [2, 4]), (‘red’, [1])])
其他功能和dict()一样。
这题其实就是拓扑排序问题,这里先来讲下拓扑排序:
一个较大的工程经常被分成许多子工程,把这些子工程称为活动。可用有向图来反映出各个活动之间的先后顺序。顶点代表活动,有向边代表活动的先后顺序。通常称这种图为顶点活动网(AOV)。一个AOV网是一个有向无环图(所以判断是否存在拓扑序列,即判断该有向图是不是无环图)。
在AOV网中,把所有活动排列成一个线性序列,使得每个活动的所有前驱活动都排在该活动的前面,把此序列叫做拓扑序列,由AOV网构造拓扑序列的过程就叫拓扑排序。
拓扑序列不唯一。
拓扑排序算法主要是循环执行两步,直到不存在入度为0的顶点为止:
1.选择一个入度为0的顶点并输出之。
2.从网中删除此顶点及所有出边。
循环结束后,若输出的顶点数小于网中的顶点数,则输出“有回路”信息,否则输出的顶点序列就是一种拓扑序列。
如这题我们用一个变量num记录输出的顶点数,若最后其等于课程数,则说明存在拓扑序列,即有可能完成所有课程的学习。
import collections
class Solution:
def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:
edges = collections.defaultdict(list)
indeg = [0]*numCourses
#建立对应邻接表和节点入度表
for pair in prerequisites:
edges[pair[1]].append(pair[0]) #键:某课程的先修课程; 值:某课程
indeg[pair[0]] += 1 #节点入度加1
#将入度为0的节点入队列
queue = collections.deque([i for i in range(numCourses) if indeg[i]==0])
#用一个变量记录被放入答案数组的节点个数,若最后它等于课程数,则存在一种拓扑排序
num = 0
while queue:
node = queue.popleft()
num += 1
for v in edges[node]:
indeg[v] -=1
if indeg[v]==0:
queue.append(v)
return num==numCourses
⭐课程表 II:

这题(课程表 II )和上题(课程表)其实是一样的,具体可看上题解释。
这题跟上题不同的是这里采用一个列表,存储每次出列的节点。即这个列表保存的是拓扑排序的结果。
import collections
class Solution:
def findOrder(self, numCourses: int, prerequisites: List[List[int]]) -> List[int]:
#建立对应邻接表和节点入度表
edges = collections.defaultdict(list)
indeg = [0]*numCourses
for pair in prerequisites:
edges[pair[1]].append(pair[0])
indeg[pair[0]] += 1
#入度为0的节点先入队列,因为拓扑排序要从入度为0的节点开始
queue = collections.deque([i for i in range(numCourses) if indeg[i]==0])
#记录返回的结果(存在拓扑排序,则返回拓扑排序的结果;不存在则返回空列表)
result = []
while queue:
node = queue.popleft()
result.append(node)
for v in edges[node]:
indeg[v] -= 1
if indeg[v]==0:
queue.append(v)
if len(result) != numCourses: return []
return result
⭐N叉树的层序遍历:
"""
# Definition for a Node.
class Node:
def __init__(self, val=None, children=None):
self.val = val
self.children = children
"""
import collections
class Solution:
def levelOrder(self, root: 'Node') -> List[List[int]]:
if not root: return []
queue = collections.deque()
queue.append(root)
result = []
while queue:
queue_len = len(queue)
temp_list = []
for i in range(queue_len):
newnode = queue.popleft()
temp_list.append(newnode.val)
if newnode.children:
for child in newnode.children:
queue.append(child)
result.append(temp_list)
return result
⭐最小高度树:


这题最容易想到的是暴力法,依次BFS遍历计算每个节点作为根节点时的高度,然后找出最小高度。但是这样做太太太太麻烦了,肯定不好。
仔细一想,我们可以从树(即无向无环图)的最外一层(叶子节点层),然后一层一层删除叶子节点,直到剩下1个或2个节点,然后这就是满足条件的根节点。为啥呢?看下图,只剩3节点时,可以看到存在高度为1和2两种情况,所以一直删除外层叶子节点,直到剩下1个或2个节点就ok。

import collections
class Solution:
def findMinHeightTrees(self, n: int, edges: List[List[int]]) -> List[int]:
if n==1: return [0]
if n==2: return [0,1]
#构建邻接表
adjs = collections.defaultdict(list)
for x in edges:
adjs[x[0]].append(x[1])
adjs[x[1]].append(x[0])
#将度为1的节点(即叶子结点)先入列,一层一层从外层去掉
queue = collections.deque([i for i in adjs if len(adjs[i])==1])
while queue:
queuelen = len(queue)
n = n - queuelen
for i in range(queuelen):
node = queue.popleft()
node_adj = adjs[node].pop() #node只有一个,将node的邻节点删除
adjs[node_adj].remove(node) #将node_adj的邻节点node也删除
#将度为1的节点(即叶子结点)入列,一层一层从外层去掉
if len(adjs[node_adj]) == 1:
queue.append(node_adj)
#若只剩1个或2个节点,则直接将它们作为满足条件的根节点返回即可
if n==1 or n==2: return list(queue)
⭐找树左下角的值:

额。。简单到爆炸,每一层从右到左遍历,一直到最后一个结点即为树的左下角节点:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
import collections
class Solution:
def findBottomLeftValue(self, root: TreeNode) -> int:
queue = collections.deque()
queue.append(root)
result = root
while queue:
queuelen = len(queue)
newnode = queue.popleft()
if(newnode.right): queue.append(newnode.right)
if(newnode.left): queue.append(newnode.left)
return newnode.val
⭐扫雷游戏:




这题的规则其实就是我们电脑中的扫雷游戏的规则,利用BFS从当前的给定的节点进行图的遍历,利用一个变量boom来记录当前节点的8个方位的地雷数;
1.若地雷数为0,则标记为‘B’(标识该节点已经或即将被打开),并入队列。因为后面出列时,会判断其8个方位是否有地雷从而再确认其是否为‘B’。
2.若地雷数不为0,则标记为地雷的数目。
即每次节点出列,都要判断这个节点的8个方位,然后对这个节点标记,和对其8个方位的节点标记为也打开或即将打开。
import collections
class Solution:
def updateBoard(self, board: List[List[str]], click: List[int]) -> List[List[str]]:
if board[click[0]][click[1]] == 'M':
board[click[0]][click[1]] = 'X'
return board
row = len(board)
col = len(board[0])
queue = collections.deque()
queue.append((click[0], click[1]))
while queue:
x, y = queue.popleft()
boom = 0 #记录当前位置的八个方位中有多少个雷
for tx,ty in [(x-1,y-1),(x-1,y),(x-1,y+1),(x+1,y-1),(x+1,y),(x+1,y+1),(x,y-1),(x,y+1)]:
if 0<=tx<row and 0<=ty<col and board[tx][ty]=='M':
boom += 1
if boom == 0:
board[x][y] = 'B'
for tx,ty in [(x-1,y-1),(x-1,y),(x-1,y+1),(x+1,y-1),(x+1,y),(x+1,y+1),(x,y-1),(x,y+1)]:
if 0<=tx<row and 0<=ty<col and board[tx][ty]=='E':
board[tx][ty] = 'B'
queue.append((tx, ty))
else: board[x][y] = str(boom)
return board
⭐完全平方数:

这题用BFS的话,重点在如何将抽象的问题转化为图的形式,比如下面这个推导图:

不过空间复杂度会消耗挺多,可以稍微剪下枝,用集合记录访问过的节点,因为节点的值相同的话,那下面的分支也是相同的。还有种可能就是下一层出现的节点的值和上一层相同,那肯定不要下一层的,因为我们这题是求最少的完全平方数的数量。所以用集合记录访问过的节点即可达到这个目的咯。
import collections
import math
class Solution:
def numSquares(self, n: int) -> int:
queue = collections.deque()
# 用队列来存储当前遍历的节点和层数(层数即最后要返回的结果)
visited = set()
#用集合来存放已经遍历过的节点
queue.append((n, 0))
while queue:
num, step = queue.popleft()
#遍历1到sqrt(num)个数,因为sqrt(num)的平方就是num
targets = [num-i*i for i in range(1, int(math.sqrt(num))+1)]
for t in targets:
if t==0:
return step+1
if t>0 and t not in visited:
visited.add(t)
queue.append((t, step+1))
如果我们知道一个数学定理(四平方和定理)的话,可以借用数学定理解决这题,而不用BFS。这种数学方法无疑是最快的。

import math
class Solution:
def numSquares(self, n: int) -> int:
# 数学方法,四平方和定理:任何一个正整数都能表示为至多四个完全平方数的和,且当n != (4**k)*(8m+7)时至多由3个组成
# 看是否为四个组成
def number4(n):
while n % 4 == 0:
n //= 4
return n % 8 == 7
# 判断当前数是否为完全平方数
def is_num(n):
return int(sqrt(n)) ** 2 == n
if is_num(n): return 1
if number4(n): return 4
# 再判断是否由2个完全平方数构成,若不是,则为3个
for i in range(1, int(sqrt(n)) + 1):
# 减去1个完全平方数还是完全平方数
if is_num(n - i * i):
return 2
return 3
⭐零钱兑换:

和上面那题(完全平方数)类似的思路,也是用BFS。
也采用集合记录已访问过的节点,因为若节点的值在集合中,说明该值已被计算过了,因为BFS是按层序遍历,若节点的值在集合中则表明,前面的(上层的)计算已经用了更少的硬币个数去组合,所以就没必要在重复计算该节点了。
import collections
class Solution:
def coinChange(self, coins: List[int], amount: int) -> int:
#遇到这中特殊情况直接返回0
if amount == 0: return 0
queue = collections.deque()
queue.append((amount, 0))
visited = set()
while queue:
num, step = queue.popleft()
targets = [num-i for i in coins]
for t in targets:
if t == 0:
return step+1
elif t>0 and t not in visited:
queue.append((t, step+1))
visited.add(t)
return -1