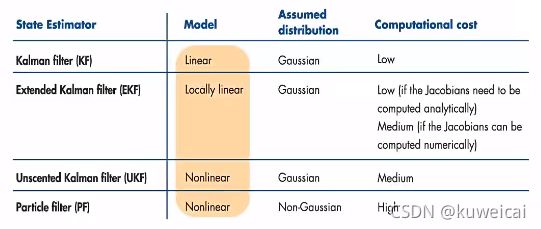
多目标跟踪(MOT)中的卡尔曼滤波(Kalman filter)和匈牙利(Hungarian)算法详解
多目标跟踪(MOT)中的卡尔曼滤波(Kalman filter)和匈牙利(Hungarian)算法详解
1. 概览
在开始具体讨论卡尔曼滤波和匈牙利算法之前,首先我们来看一下基于检测的目标跟踪算法的大致流程。
2. 卡尔曼滤波(Kalman filter)
目标跟踪中使用的就是最基础的 Kalman filter 算法。这里也仅仅讨论最基础的 Kalman filter 算法。
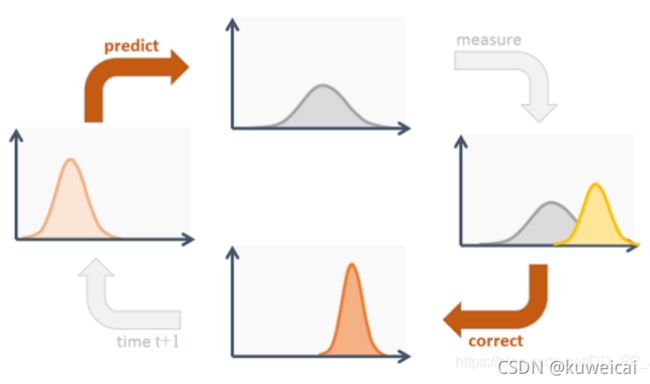
卡尔曼滤波算法的过程很简单,如下图所示。最核心的两个步骤就是预测和更新(下图的 correct)。
在目标跟踪任务中,目标的状态变量表示为 x , y , a , h , v x , v y , v a , v h x, y, a, h, vx, vy, va, vh x,y,a,h,vx,vy,va,vh,其中 x , y x, y x,y 表示目标框的中心坐标, a a a 表示目标框的高宽比, h h h 表示目标框的高,在卡尔曼滤波算法中也表示为 mean; v x , v y , v a , v h vx, vy, va, vh vx,vy,va,vh 分别表示对于变量的速度,也称之为 covariance。在 DeepSORT 和 ByteTrack 算法中都是使用的具有等速运动和线性观测模型的标准卡尔曼滤波器。
2.1 预测
预测就是根据目标在 t-1 时刻的状态来预测其在 t 时刻的状态。预测主要分为两部分。
{ x ′ = F x ( 1 ) P ′ = F P F T + Q ( 2 ) \left\{\begin{aligned} & x' = Fx &(1)\\ & P' = FPF^T + Q &(2) \end{aligned}\right. { x′=FxP′=FPFT+Q(1)(2)
在公式 1 中,x 为 track 在 t-1 时刻的均值,F 称为 状态转移矩阵,该公式预测 t 时刻的 x’。
在公式 2 中,P 为 track 在 t-1 时刻的协方差,Q 为系统的噪声矩阵,代表整个系统的可靠程度,一般初始化为很小的值,该公式预测 t 时刻的 P’。
对于的代码如下。
def predict(self, mean, covariance):
"""Run Kalman filter prediction step.
Parameters
----------
mean : ndarray
The 8 dimensional mean vector of the object state at the previous
time step.
covariance : ndarray
The 8x8 dimensional covariance matrix of the object state at the
previous time step.
Returns
-------
(ndarray, ndarray)
Returns the mean vector and covariance matrix of the predicted
state. Unobserved velocities are initialized to 0 mean.
"""
std_pos = [
self._std_weight_position * mean[0],
self._std_weight_position * mean[1],
1 * mean[2],
self._std_weight_position * mean[3]]
std_vel = [
self._std_weight_velocity * mean[0],
self._std_weight_velocity * mean[1],
0.1 * mean[2],
self._std_weight_velocity * mean[3]]
motion_cov = np.diag(np.square(np.r_[std_pos, std_vel])) # 噪声矩阵Q
mean = np.dot(self._motion_mat, mean) # x'=Fx
covariance = np.linalg.multi_dot((
self._motion_mat, covariance, self._motion_mat.T)) + motion_cov # P' = FPF(T) + Q
return mean, covariance
关于 F 和 Q 的初始化是在 _init_() 函数中进行的。
def __init__(self):
ndim, dt = 4, 1.
# Create Kalman filter model matrices.
self._motion_mat = np.eye(2 * ndim, 2 * ndim) # 状态转移矩阵 F
for i in range(ndim):
self._motion_mat[i, ndim + i] = dt
self._update_mat = np.eye(ndim, 2 * ndim) # 测量矩阵 H
# Motion and observation uncertainty are chosen relative to the current
# state estimate. These weights control the amount of uncertainty in
# the model. This is a bit hacky.
self._std_weight_position = 1. / 20
self._std_weight_velocity = 1. / 160
F 的取值如下。
2.2 更新
更新是基于 t 时刻的检测结果(测量值)和根据跟踪轨迹预测目标在 t 时刻的状态(预测值),得到一个在 t 时刻更精确的结果(状态)。
{ y = z − H x ′ ( 3 ) S = H P ′ H T + R ( 4 ) K = P ′ H T S − 1 ( 5 ) x = x ′ + K y ( 6 ) P = ( I − K H ) P ′ ( 7 ) \left\{\begin{aligned} & y = z - Hx' &(3)\\ & S = HP'H^T + R &(4) \\ & K = P'H^TS^{-1} &(5)\\ & x = x' + Ky &(6)\\ & P = (I - KH)P' &(7) \\ \end{aligned}\right. ⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧y=z−Hx′S=HP′HT+RK=P′HTS−1x=x′+KyP=(I−KH)P′(3)(4)(5)(6)(7)
在公式 3 中,z 为 detection 的均值向量(均值向量的计算在 initiate() 函数中进行 ),不包含速度变化值,即 z=[x, y, a, h],H 称为测量矩阵,它将 track 的均值向量 x’ 映射到检测空间,该公式计算 detection 和 track 的均值误差 y;
测量矩阵 H 的取值如下。
在公式 4 中,R 为检测器的 噪声矩阵,它是一个 4x4 的对角矩阵,对角线上的值分别为中心点两个坐标以及宽高的噪声,以任意值初始化,一般设置宽高的噪声大于中心点的噪声。该公式先将协方差矩阵 P’ 映射到检测空间,然后再加上噪声矩阵 R;
在公式 5 中,计算**卡尔曼增益 K,**卡尔曼增益用于估计误差的重要程度;
在公式 6 和公式 7 中,计算更新后的均值向量 x 和协方差矩阵 P。
更新的代码如下。
def initiate(self, measurement):
"""Create track from unassociated measurement.
Parameters
----------
measurement : ndarray
Bounding box coordinates (x, y, a, h) with center position (x, y),
aspect ratio a, and height h.
Returns
-------
(ndarray, ndarray)
Returns the mean vector (8 dimensional) and covariance matrix (8x8
dimensional) of the new track. Unobserved velocities are initialized
to 0 mean.
"""
mean_pos = measurement
mean_vel = np.zeros_like(mean_pos)
mean = np.r_[mean_pos, mean_vel] # 按列拼接
std = [
2 * self._std_weight_position * measurement[0], # the center point x
2 * self._std_weight_position * measurement[1], # the center point y
1 * measurement[2], # the ratio of width/height
2 * self._std_weight_position * measurement[3], # the height
10 * self._std_weight_velocity * measurement[0],
10 * self._std_weight_velocity * measurement[1],
0.1 * measurement[2],
10 * self._std_weight_velocity * measurement[3]]
covariance = np.diag(np.square(std))
return mean, covariance
def project(self, mean, covariance):
"""Project state distribution to measurement space.
Parameters
----------
mean : ndarray
The state's mean vector (8 dimensional array).
covariance : ndarray
The state's covariance matrix (8x8 dimensional).
Returns
-------
(ndarray, ndarray)
Returns the projected mean and covariance matrix of the given state
estimate.
"""
# R 测量过程中噪声的协方差
std = [
self._std_weight_position * mean[3],
self._std_weight_position * mean[3],
1e-1,
self._std_weight_position * mean[3]]
# 初始化噪声矩阵R
innovation_cov = np.diag(np.square(std))
# 将均值向量映射到检测空间,即Hx'
mean = np.dot(self._update_mat, mean)
# 将协方差矩阵映射到检测空间,即HP'H^T
covariance = np.linalg.multi_dot((
self._update_mat, covariance, self._update_mat.T))
return mean, covariance + innovation_cov # Hx', S
def update(self, mean, covariance, measurement):
"""Run Kalman filter correction step.
Parameters
----------
mean : ndarray
The predicted state's mean vector (8 dimensional).
covariance : ndarray
The state's covariance matrix (8x8 dimensional).
measurement : ndarray
The 4 dimensional measurement vector (x, y, a, h), where (x, y)
is the center position, a the aspect ratio, and h the height of the
bounding box.
Returns
-------
(ndarray, ndarray)
Returns the measurement-corrected state distribution.
"""
# 通过估计值和观测值估计最新结果
# 将均值和协方差映射到检测空间,得到 Hx' 和 S
projected_mean, projected_cov = self.project(mean, covariance)
# 矩阵分解
chol_factor, lower = scipy.linalg.cho_factor(
projected_cov, lower=True, check_finite=False)
# 计算卡尔曼增益K
kalman_gain = scipy.linalg.cho_solve(
(chol_factor, lower), np.dot(covariance, self._update_mat.T).T,
check_finite=False).T
# z - Hx'
innovation = measurement - projected_mean
# x = x' + Ky
new_mean = mean + np.dot(innovation, kalman_gain.T)
# P = (I - KH)P'
new_covariance = covariance - np.linalg.multi_dot((
kalman_gain, projected_cov, kalman_gain.T))
return new_mean, new_covariance # 返回更新后的 mean 和 covariance
2.3 gating_distance
除了上面的更新和预测之外,卡尔曼滤波算法中还有个方法用于计算 gating distance。计算的结果主要用于后续匹配作为代价矩阵。在 Deep SORT 中由于引入了特征信息,gating distance 作为一个阈值过滤掉一部分特征信息(比如距离比较大的目标,就不需要做特征匹配了),在 ByteTrack 中,仅仅使用位置信息,直接将其作为代价函数。这里采用的是马氏距离(Mahalanobis distance )。那为什么是马氏距离,而不是更常用的欧式,马哈顿或者余弦距离了,这样主要是状态变量(8维数据)在不同的帧中有不同的分布,仅仅简单地使用余弦距离或欧式距离来比较卡尔曼滤波预测和神经网络测量是不合理的,因为它们几乎不涉及数据分布。而马氏距离不受量纲的影响,两点之间的马氏距离与原始数据的测量单位无关。更多关于马氏距离的接受可以参考 马氏距离。
def gating_distance(self, mean, covariance, measurements,
only_position=False):
"""Compute gating distance between state distribution and measurements.
A suitable distance threshold can be obtained from `chi2inv95`. If
`only_position` is False, the chi-square distribution has 4 degrees of
freedom, otherwise 2.
Parameters
----------
mean : ndarray
Mean vector over the state distribution (8 dimensional).
covariance : ndarray
Covariance of the state distribution (8x8 dimensional).
measurements : ndarray
An Nx4 dimensional matrix of N measurements, each in
format (x, y, a, h) where (x, y) is the bounding box center
position, a the aspect ratio, and h the height.
only_position : Optional[bool]
If True, distance computation is done with respect to the bounding
box center position only.
Returns
-------
ndarray
Returns an array of length N, where the i-th element contains the
squared Mahalanobis distance between (mean, covariance) and
`measurements[i]`.
"""
mean, covariance = self.project(mean, covariance)
if only_position:
mean, covariance = mean[:2], covariance[:2, :2]
measurements = measurements[:, :2]
cholesky_factor = np.linalg.cholesky(covariance)
d = measurements - mean
z = scipy.linalg.solve_triangular(
cholesky_factor, d.T, lower=True, check_finite=False,
overwrite_b=True)
squared_maha = np.sum(z * z, axis=0)
return squared_maha
3. 匈牙利(Hungarian)算法
匈牙利算法由 Harold Kuhn 于 1955 年开发并出版,他命名为“匈牙利方法”,因为该算法主要基于两位匈牙利数学家 Dénes Kőnig 和 Jenő Egerváry 的早期作品。James Munkres 在 1957 年回顾了该算法并观察到它是(强)多项式的。从那时起,该算法也被称为 Kuhn-Munkres 算法 或 Munkres 分配算法。原算法的时间复杂度为 O ( n 4 ) O(n^{4}) O(n4),但是Edmonds和Karp以及独立的 Tomizawa 注意到可以对其进行修改以实现 O ( n 3 ) O(n^{3}) O(n3) 运行时间。
匈牙利算法通常用来求二分图的最大匹配数和最小点覆盖数。二分图就是分为两组的数据,前后两组直接可以相连,但是同组直接不能相连。就好比目标跟踪中,视频前后帧中的检测框,可以看做是两组数据,这两组数据之间存在匹配关系(同一个目标,在前后帧中的检测框为一对),而同一帧中的目标框经过 NMS 之后,我们认为他们都是不同的目标,不存在匹配关系。显然 MOT 中前后帧中目标框的匹配问题就是一个求二分图的最大匹配数的问题(尽量匹配所有目标)。
匈牙利算法需要输入一个代价矩阵(或者利益矩阵),那么在目标跟踪问题中,代价矩阵可以是从前后帧中提取的 ReID 特征的距离,也可以是 IoU 的距离,显然距离越小,匹配的就越好,所以整个问题就变成找到一组匹配,使得总的代价最小。
比如上面的表格中的列(Track ID)是之前跟踪到的目标,行(Detection ID)是当前检测到的目标,[1, 1] 表示的是 Track ID 1 和 Detection ID 1 的 IoU 距离。
如果想了解匈牙利算法的原理,可以参考 匈牙利算法,但是这是最简单的不带权重的情况(也有把带权重的称为 KM 算法),仅仅是能不能匹配。更具体的可以参考附录的代码,其计算原理参考自 匈牙利算法原理。代码来自 hungarian.py 。
当然在实际使用中,我们可以直接调用相关的库来完成相关计算。比如在 DeepSORT 中,使用的是 linear_sum_assignment 来计算的。
from scipy.optimize import linear_sum_assignment as linear_assignment
row_indices, col_indices = linear_assignment(cost_matrix)
在 ByteTrack 中是使用的 lap 库中的 lapjv 函数来计算的。lapjv 的时间复杂度也是 O ( n 3 ) O(n^{3}) O(n3),但是实际使用中速度较 linear_sum_assignment 快。
import lap
cost, x, y = lap.lapjv(cost_matrix, extend_cost=True, cost_limit=thresh)
附录
- ByteTrack-卡尔曼滤波
- 匈牙利算法
# hungarian.py
import numpy as np
class HungarianError(Exception):
pass
class Hungarian:
"""
Implementation of the Hungarian (Munkres) Algorithm using np.
Usage:
hungarian = Hungarian(cost_matrix)
hungarian.calculate()
or
hungarian = Hungarian()
hungarian.calculate(cost_matrix)
Handle Profit matrix:
hungarian = Hungarian(profit_matrix, is_profit_matrix=True)
or
cost_matrix = Hungarian.make_cost_matrix(profit_matrix)
The matrix will be automatically padded if it is not square.
For that numpy's resize function is used, which automatically adds 0's to any row/column that is added
Get results and total potential after calculation:
hungarian.get_results()
hungarian.get_total_potential()
"""
def __init__(self, input_matrix=None, is_profit_matrix=False):
"""
input_matrix is a List of Lists.
input_matrix is assumed to be a cost matrix unless is_profit_matrix is True.
"""
if input_matrix is not None:
# Save input
my_matrix = np.array(input_matrix)
self._input_matrix = np.array(input_matrix)
self._maxColumn = my_matrix.shape[1]
self._maxRow = my_matrix.shape[0]
# Adds 0s if any columns/rows are added. Otherwise stays unaltered
matrix_size = max(self._maxColumn, self._maxRow)
pad_columns = matrix_size - self._maxRow
pad_rows = matrix_size - self._maxColumn
my_matrix = np.pad(my_matrix, ((0,pad_columns),(0,pad_rows)), 'constant', constant_values=(0))
# Convert matrix to profit matrix if necessary
if is_profit_matrix:
my_matrix = self.make_cost_matrix(my_matrix)
self._cost_matrix = my_matrix
self._size = len(my_matrix)
self._shape = my_matrix.shape
# Results from algorithm.
self._results = []
self._totalPotential = 0
else:
self._cost_matrix = None
def get_results(self):
"""Get results after calculation."""
return self._results
def get_total_potential(self):
"""Returns expected value after calculation."""
return self._totalPotential
def calculate(self, input_matrix=None, is_profit_matrix=False):
"""
Implementation of the Hungarian (Munkres) Algorithm.
input_matrix is a List of Lists.
input_matrix is assumed to be a cost matrix unless is_profit_matrix is True.
"""
# Handle invalid and new matrix inputs.
if input_matrix is None and self._cost_matrix is None:
raise HungarianError("Invalid input")
elif input_matrix is not None:
self.__init__(input_matrix, is_profit_matrix)
result_matrix = self._cost_matrix.copy()
# Step 1: Subtract row mins from each row.
for index, row in enumerate(result_matrix):
result_matrix[index] -= row.min()
# Step 2: Subtract column mins from each column.
for index, column in enumerate(result_matrix.T):
result_matrix[:, index] -= column.min()
# Step 3: Use minimum number of lines to cover all zeros in the matrix.
# If the total covered rows+columns is not equal to the matrix size then adjust matrix and repeat.
total_covered = 0
while total_covered < self._size:
# Find minimum number of lines to cover all zeros in the matrix and find total covered rows and columns.
cover_zeros = CoverZeros(result_matrix)
covered_rows = cover_zeros.get_covered_rows()
covered_columns = cover_zeros.get_covered_columns()
total_covered = len(covered_rows) + len(covered_columns)
# if the total covered rows+columns is not equal to the matrix size then adjust it by min uncovered num (m).
if total_covered < self._size:
result_matrix = self._adjust_matrix_by_min_uncovered_num(result_matrix, covered_rows, covered_columns)
# Step 4: Starting with the top row, work your way downwards as you make assignments.
# Find single zeros in rows or columns.
# Add them to final result and remove them and their associated row/column from the matrix.
expected_results = min(self._maxColumn, self._maxRow)
zero_locations = (result_matrix == 0)
while len(self._results) != expected_results:
# If number of zeros in the matrix is zero before finding all the results then an error has occurred.
if not zero_locations.any():
raise HungarianError("Unable to find results. Algorithm has failed.")
# Find results and mark rows and columns for deletion
matched_rows, matched_columns = self.__find_matches(zero_locations)
# Make arbitrary selection
total_matched = len(matched_rows) + len(matched_columns)
if total_matched == 0:
matched_rows, matched_columns = self.select_arbitrary_match(zero_locations)
# Delete rows and columns
for row in matched_rows:
zero_locations[row] = False
for column in matched_columns:
zero_locations[:, column] = False
# Save Results
self.__set_results(zip(matched_rows, matched_columns))
# Calculate total potential
value = 0
for row, column in self._results:
value += self._input_matrix[row, column]
self._totalPotential = value
@staticmethod
def make_cost_matrix(profit_matrix):
"""
Converts a profit matrix into a cost matrix.
Expects NumPy objects as input.
"""
# subtract profit matrix from a matrix made of the max value of the profit matrix
matrix_shape = profit_matrix.shape
offset_matrix = np.ones(matrix_shape, dtype=int) * profit_matrix.max()
cost_matrix = offset_matrix - profit_matrix
return cost_matrix
def _adjust_matrix_by_min_uncovered_num(self, result_matrix, covered_rows, covered_columns):
"""Subtract m from every uncovered number and add m to every element covered with two lines."""
# Calculate minimum uncovered number (m)
elements = []
for row_index, row in enumerate(result_matrix):
if row_index not in covered_rows:
for index, element in enumerate(row):
if index not in covered_columns:
elements.append(element)
min_uncovered_num = min(elements)
# Add m to every covered element
adjusted_matrix = result_matrix
for row in covered_rows:
adjusted_matrix[row] += min_uncovered_num
for column in covered_columns:
adjusted_matrix[:, column] += min_uncovered_num
# Subtract m from every element
m_matrix = np.ones(self._shape, dtype=int) * min_uncovered_num
adjusted_matrix -= m_matrix
return adjusted_matrix
def __find_matches(self, zero_locations):
"""Returns rows and columns with matches in them."""
marked_rows = np.array([], dtype=int)
marked_columns = np.array([], dtype=int)
# Mark rows and columns with matches
# Iterate over rows
for index, row in enumerate(zero_locations):
row_index = np.array([index])
if np.sum(row) == 1:
column_index, = np.where(row)
marked_rows, marked_columns = self.__mark_rows_and_columns(marked_rows, marked_columns, row_index,
column_index)
# Iterate over columns
for index, column in enumerate(zero_locations.T):
column_index = np.array([index])
if np.sum(column) == 1:
row_index, = np.where(column)
marked_rows, marked_columns = self.__mark_rows_and_columns(marked_rows, marked_columns, row_index,
column_index)
return marked_rows, marked_columns
@staticmethod
def __mark_rows_and_columns(marked_rows, marked_columns, row_index, column_index):
"""Check if column or row is marked. If not marked then mark it."""
new_marked_rows = marked_rows
new_marked_columns = marked_columns
if not (marked_rows == row_index).any() and not (marked_columns == column_index).any():
new_marked_rows = np.insert(marked_rows, len(marked_rows), row_index)
new_marked_columns = np.insert(marked_columns, len(marked_columns), column_index)
return new_marked_rows, new_marked_columns
@staticmethod
def select_arbitrary_match(zero_locations):
"""Selects row column combination with minimum number of zeros in it."""
# Count number of zeros in row and column combinations
rows, columns = np.where(zero_locations)
zero_count = []
for index, row in enumerate(rows):
total_zeros = np.sum(zero_locations[row]) + np.sum(zero_locations[:, columns[index]])
zero_count.append(total_zeros)
# Get the row column combination with the minimum number of zeros.
indices = zero_count.index(min(zero_count))
row = np.array([rows[indices]])
column = np.array([columns[indices]])
return row, column
def __set_results(self, result_lists):
"""Set results during calculation."""
# Check if results values are out of bound from input matrix (because of matrix being padded).
# Add results to results list.
for result in result_lists:
row, column = result
if row < self._maxRow and column < self._maxColumn:
new_result = (int(row), int(column))
self._results.append(new_result)
class CoverZeros:
"""
Use minimum number of lines to cover all zeros in the matrix.
Algorithm based on: http://weber.ucsd.edu/~vcrawfor/hungar.pdf
"""
def __init__(self, matrix):
"""
Input a matrix and save it as a boolean matrix to designate zero locations.
Run calculation procedure to generate results.
"""
# Find zeros in matrix
self._zero_locations = (matrix == 0)
self._shape = matrix.shape
# Choices starts without any choices made.
self._choices = np.zeros(self._shape, dtype=bool)
self._marked_rows = []
self._marked_columns = []
# marks rows and columns
self.__calculate()
# Draw lines through all unmarked rows and all marked columns.
self._covered_rows = list(set(range(self._shape[0])) - set(self._marked_rows))
self._covered_columns = self._marked_columns
def get_covered_rows(self):
"""Return list of covered rows."""
return self._covered_rows
def get_covered_columns(self):
"""Return list of covered columns."""
return self._covered_columns
def __calculate(self):
"""
Calculates minimum number of lines necessary to cover all zeros in a matrix.
Algorithm based on: http://weber.ucsd.edu/~vcrawfor/hungar.pdf
"""
while True:
# Erase all marks.
self._marked_rows = []
self._marked_columns = []
# Mark all rows in which no choice has been made.
for index, row in enumerate(self._choices):
if not row.any():
self._marked_rows.append(index)
# If no marked rows then finish.
if not self._marked_rows:
return True
# Mark all columns not already marked which have zeros in marked rows.
num_marked_columns = self.__mark_new_columns_with_zeros_in_marked_rows()
# If no new marked columns then finish.
if num_marked_columns == 0:
return True
# While there is some choice in every marked column.
while self.__choice_in_all_marked_columns():
# Some Choice in every marked column.
# Mark all rows not already marked which have choices in marked columns.
num_marked_rows = self.__mark_new_rows_with_choices_in_marked_columns()
# If no new marks then Finish.
if num_marked_rows == 0:
return True
# Mark all columns not already marked which have zeros in marked rows.
num_marked_columns = self.__mark_new_columns_with_zeros_in_marked_rows()
# If no new marked columns then finish.
if num_marked_columns == 0:
return True
# No choice in one or more marked columns.
# Find a marked column that does not have a choice.
choice_column_index = self.__find_marked_column_without_choice()
while choice_column_index is not None:
# Find a zero in the column indexed that does not have a row with a choice.
choice_row_index = self.__find_row_without_choice(choice_column_index)
# Check if an available row was found.
new_choice_column_index = None
if choice_row_index is None:
# Find a good row to accomodate swap. Find its column pair.
choice_row_index, new_choice_column_index = \
self.__find_best_choice_row_and_new_column(choice_column_index)
# Delete old choice.
self._choices[choice_row_index, new_choice_column_index] = False
# Set zero to choice.
self._choices[choice_row_index, choice_column_index] = True
# Loop again if choice is added to a row with a choice already in it.
choice_column_index = new_choice_column_index
def __mark_new_columns_with_zeros_in_marked_rows(self):
"""Mark all columns not already marked which have zeros in marked rows."""
num_marked_columns = 0
for index, column in enumerate(self._zero_locations.T):
if index not in self._marked_columns:
if column.any():
row_indices, = np.where(column)
zeros_in_marked_rows = (set(self._marked_rows) & set(row_indices)) != set([])
if zeros_in_marked_rows:
self._marked_columns.append(index)
num_marked_columns += 1
return num_marked_columns
def __mark_new_rows_with_choices_in_marked_columns(self):
"""Mark all rows not already marked which have choices in marked columns."""
num_marked_rows = 0
for index, row in enumerate(self._choices):
if index not in self._marked_rows:
if row.any():
column_index, = np.where(row)
if column_index in self._marked_columns:
self._marked_rows.append(index)
num_marked_rows += 1
return num_marked_rows
def __choice_in_all_marked_columns(self):
"""Return Boolean True if there is a choice in all marked columns. Returns boolean False otherwise."""
for column_index in self._marked_columns:
if not self._choices[:, column_index].any():
return False
return True
def __find_marked_column_without_choice(self):
"""Find a marked column that does not have a choice."""
for column_index in self._marked_columns:
if not self._choices[:, column_index].any():
return column_index
raise HungarianError(
"Could not find a column without a choice. Failed to cover matrix zeros. Algorithm has failed.")
def __find_row_without_choice(self, choice_column_index):
"""Find a row without a choice in it for the column indexed. If a row does not exist then return None."""
row_indices, = np.where(self._zero_locations[:, choice_column_index])
for row_index in row_indices:
if not self._choices[row_index].any():
return row_index
# All rows have choices. Return None.
return None
def __find_best_choice_row_and_new_column(self, choice_column_index):
"""
Find a row index to use for the choice so that the column that needs to be changed is optimal.
Return a random row and column if unable to find an optimal selection.
"""
row_indices, = np.where(self._zero_locations[:, choice_column_index])
for row_index in row_indices:
column_indices, = np.where(self._choices[row_index])
column_index = column_indices[0]
if self.__find_row_without_choice(column_index) is not None:
return row_index, column_index
# Cannot find optimal row and column. Return a random row and column.
from random import shuffle
shuffle(row_indices)
column_index, = np.where(self._choices[row_indices[0]])
return row_indices[0], column_index[0]
if __name__ == '__main__':
cost_matrix = [
[4, 2, 8],
[4, 3, 7],
[3, 1, 6]]
hungarian = Hungarian(cost_matrix)
print('calculating...')
hungarian.calculate()
print("Expected value:\t\t12")
print("Calculated value:\t", hungarian.get_total_potential()) # = 12
print("Expected results:\n\t", "[(0, 1), (1, 0), (2, 2)]")
print("Results:\n\t", hungarian.get_results())
print("-" * 80)
参考
- 如何通俗并尽可能详细地解释卡尔曼滤波?
- 匈牙利算法
- wiki-匈牙利算法