2021年华中杯A题（马赛克瓷砖选色问题）详细分析

文章目录

一、基本介绍

1.1 题目描述

1.2 待解决问题

二、问题分析与求解

2.1 问题一分析与求解

 2.2 问题二分析与求解

 2.3 问题三分析与求解

 三、总结

---

一、基本介绍

1.1 题目描述

马赛克瓷砖是一种尺寸较小（常见规格为边长不超过 5cm）的正方形瓷砖，便于在非平整的表面铺设，并且容易拼接组合出各种文字或图案。但是受工艺和成本的限制，瓷砖的颜色只能是有限的几种。用户在拼接图案时，首先要根据原图中的颜色，选出颜色相近的瓷砖，才能进行拼接。

某马赛克瓷砖生产厂只能生产 22 种颜色（见附件 1）的马赛克瓷砖。该厂要开发一个软件，能够根据原始图片的颜色，自动找出颜色最接近的瓷砖，以减少客户人工选色的工作量。该厂希望你们团队提供确定原始颜色与瓷砖颜色对应关系的算法。假设原始图像为24位真彩色格式，即 R、G、B 三个颜色分量均为 8 位，共有28 × 28 × 28 = 16777216种颜色，对于任何一种指定的颜色，算法输出颜色最相近的瓷砖的颜色编号。

1.2 待解决问题

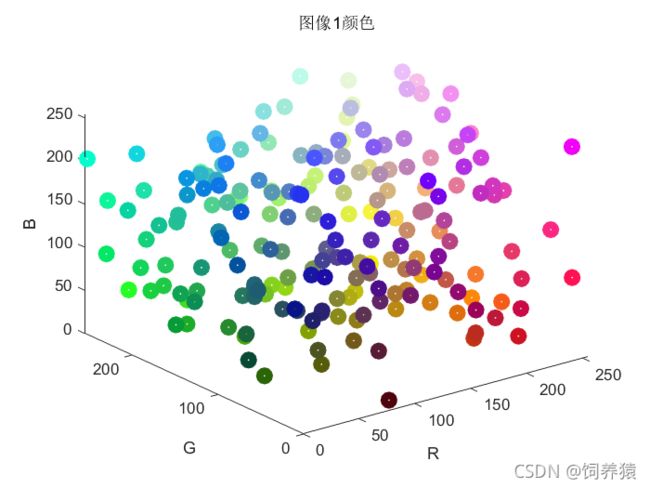
（1）附件 2 是图像 1 中的 216 种颜色，附件 3 是图像 2 中的 200 种颜色，请找出与每种颜色最接近的瓷砖颜色，将选出的瓷砖颜色的编号按照附件 4 的要求输出至结果文件。

（2）如果该厂技术革新，计划研发新颜色的瓷砖。那么，不考虑研发难度，只考虑到拼接图像的表现力，应该优先增加哪些颜色的瓷砖？当同时增加 1 种颜色、同时增加 2 种颜色、……、同时增加 10 种颜色时，分别给出对应颜色的RGB 编码值。

（3） 如果研发一种新颜色瓷砖的成本是相同的，与颜色本身无关，那么，综合考虑成本和表现效果，你们建议新增哪几种颜色，说明理由并给出对应的RGB 编码值。

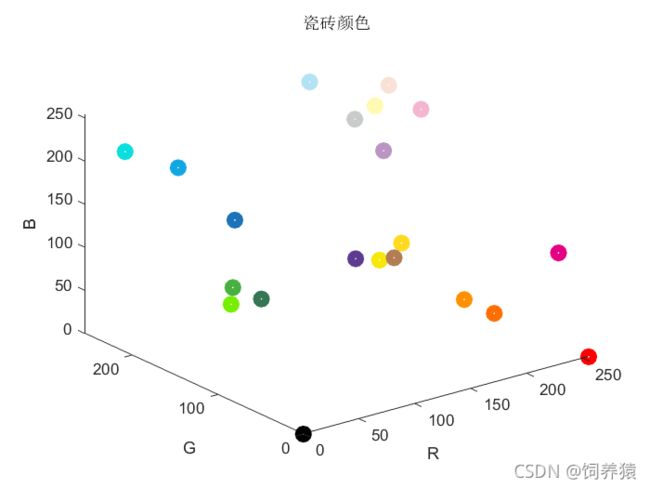
现有瓷砖颜色

二、问题分析与求解

2.1 问题一分析与求解

针对问题一，我们首先引入了色差这一概念来表示不同颜色之间的相似度，并且将颜色对象坐标化，利用欧式距离公式，求得两点之间的距离值，并将此值赋予色差，通过计算得到色差值的大小来表示不同颜色之间的相似程度。并且，我们首先选择了 RGB 空间、HSV 空间和 Lab 空间三种颜色空间，对三种不同颜色空间的特性进行了阐释，并且三种空间中均建立了各自的颜色匹配模型。之后，我们对三种空间以及各自所建立的模型进行评估比较，最终选定使用 Lab 空间模型以及根据该模型建立的颜色匹配模型，并在求解过程中进行简化运算，最终求得与附件 2、3 中 216 种颜色和 200 种颜色最接近的颜色，以及 RGB 编码值。

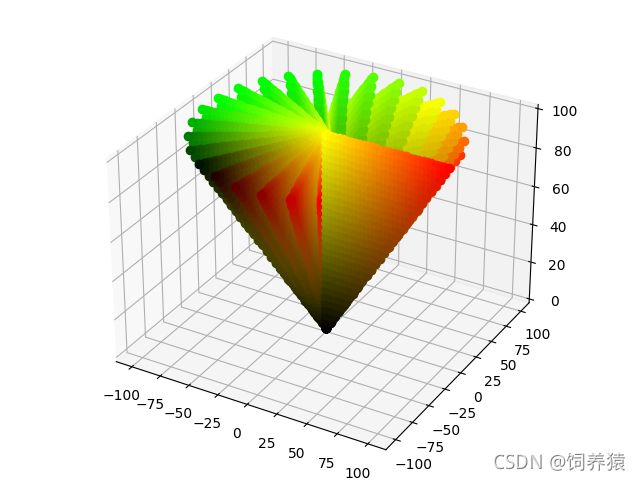
#HSV 的三维锥形图像代码
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
from math import sin, cos, pi
#进行
# r,g,b [0,255]
# h 0 - 360
# s 0 - 100
# v 0 - 100
def rgb2hsv(r, g, b):
    r_, g_, b_ = r / 255, g / 255, b / 255
    c_max = max(r_, g_, b_)
    c_min = min(r_, g_, b_)
    dela = c_max - c_min
    if dela == 0:
        h = 0
    elif c_max == r_ and g_ >= b_:\
            h = 60 * ((g_ - b_) / dela + 0)
    elif c_max == r_ and g_ < b_:
        h = 60 * ((g_ - b_) / dela + 2)
    elif c_max == g_:
        h = 60 * ((b_ - r_) / dela + 2)
    else:
        h = 60 * ((r_ - g_) / dela + 4)
        s = 0 if c_max == 0 else dela / c_max
        v = c_max
        return h, s * 100, v * 100
# h 0,255 s,v 0,1
def hsv2rgb(h, s, v):
    c = v * s
    x = c * (1 - abs((h / 60) % 2-1))
    m = v - c
    if 0 <= h < 60:
        r_, g_, b_ = c, x, 0
    elif 60 <= h <= 120:
        r_, g_, b_ = x, c, 0
    elif 120 <= h <= 180:
        r_, g_, b_ = 0, c, x
    elif 180 <= h <= 240:
        r_, g_, b_ = 0, x, c
    elif 240 <= h <= 300:
        r_, g_, b_ = x, 0, c
    elif 300 <= h <= 360:
        r_, g_, b_ = c, 0, x
    return (r_ + m) * 255, (g_ + m) * 255, (b_ + m)
fig = plt.figure() # 定义新的三维坐标轴
ax = Axes3D(fig)
size = 30
points = np.linspace(0, 255, size).astype(np.int32)
for h in np.linspace(0, 360, size):
    for s in np.linspace(0, 100, size):
        for v in np.linspace(0, 100, size):
            if v < s:
                continue
            x_ = s * cos(h * pi / 180)
            y_ = s * sin(h * pi / 180)
            # z_ = -(v ** 2 - s ** 2) ** 0.5
            z_ = v
            x, y, z = hsv2rgb(h, s / 100, v / 100)
            ax.plot([x_], [y_], [z_], "ro", color=(x / 255, y / 255, z / 255, 1))
plt.show()
print('---')

 

 

import sys
import math
#本代码是针对题目来的，附件2是图像1中的216种颜色，附件3是图像2中的200种颜色。附件2的选色结果保存在result1.txt中。附件3的选色结果保存在result2.txt中。
filename1=sys.argv[1]#用来接收附件2
filename2=sys.argv[2]#附件3
filename3=sys.argv[3]#数据输出result1。txt
filename4=sys.argv[4]#数据输出result2。txt
f1=open(filename1,'r',encoding='utf8')#读入
f2=open(filename2,'r',encoding='utf8')#读入
f3=open(filename3,'w',encoding='utf8')#输出result1.txt
f4=open(filename4,'w',encoding='utf8')#输出result2.txt
s="序号,瓷砖颜色编号"+'\n'
f3.writelines(s)#先把格式输出
f4.writelines(s)
b=[[0,0,0],[255,255,255],[255,0,0],[246,232,9],[72,176,64],[27,115,186],[53,118,84],[244,181,208],[255,145,0],[177,125,85],[92,59,144],[11,222,222],[228,0,130],[255,218,32],[118,238,0],[17,168,226],[255,110,0],[201,202,202],[255,249,177],[179,226,242],[249,225,214],[186,149,195]]
def distance(a,b):#a是要被匹配的单个颜色，b为已有的颜色列表,返回最相似的颜色下标加1
    min=[442,0]#第一个参数为math.sqrt(3*(255)**2)，第二个参数表示标号，是下标加1
    for i in range(len(b)):
        min_i=math.sqrt((a[0]-b[i][0])**2+(a[1]-b[i][1])**2+(a[2]-b[i][2])**2)
        if min_i

 

 2.2 问题二分析与求解

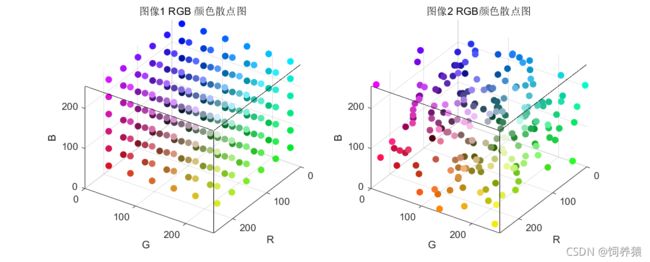
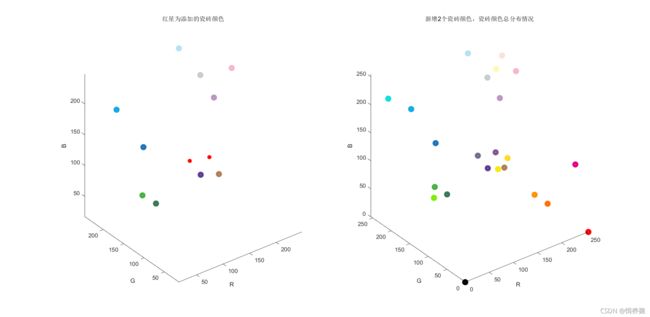
针对问题二，由于只考虑表现力效果，我们首先对附件 2、3 中的 216 种颜色 200 种颜色和已有的 22 种进行了统计与可视化处理，得出它们的颜色空间分布图，以此为基础选定需求侧与供给侧的分析入手角度，确定了表现力评估标准——“在添加颜色后，新的颜色集在空间中的分布更加均匀”。根据上述条件，优先增加与多个颜色差别较小，不管增加几种颜色，但本质上还是选近似颜色，只不过同时多增加几种颜色就要考虑新聚类中心的分布问题，FCM思想比较适合解决该问题，目标函数可以就以FCM的来 。

其中i表示聚类中心，j表示其他点，c为聚类中心总数，N为其他点总数（除了FCM也可以借助其他聚类算法的思想来做），该算法思想就是其他点到聚类中心的距离的倒数之和最小，但是别直接套用该算法程序，其中的距离公式需要更改。第二问说是从技术革新的角度，那么本问被聚类的点应当为256*256*256个点了，并不是附件2和附件3的点来做聚类分析，当然在选出新聚类中心颜色后，可以再去算一附件2和附件3的J函数值，对于题目提到的表现力，颜色越近似就说明表现力越好，表现力函数公式可以直接是J函数的倒数。

%MATLAB部分代码
%下面程序是简易版粒子群优化算法，种群大小和迭代次数设的比较小，自行调整，也可换做其他优化算法
num=20;%种群大小
k=2;%新增k个中心
c1 = 0.5; %非负常数，加速度因子
Vmax=10; %粒子最大更新速度
Vmin=-10; %粒子最小更新速度
%初始化种群
xx=[];

for i=1:num
    xx(i,:)=round(255.*rand(1,3*k));%round四舍五入
end

F=[];
for i=1:num
    YY=[];
    YY=[Y;reshape(xx(i,:)',3,k)'];%将新聚类中心添加到瓷砖颜色库中
    D=[];
    D=Dis(X,YY,a1,a2);
    D=1./D;
    D(find(D==Inf))=0;
    D=sum(D,2);
    D=1./D;
    F(i,1)=sum(D);
end
[bestf,in]=min(F);
bestx=xx(in,:);
trace(1)=bestf;
det=20;%迭代次数
slexx=xx;
for ii=1:det
    V=rands(num,k*3);
    for j=1:num
        V(j,:)=V(j,:)+c1*rand.*(bestx-slexx(j,:));
    end
    V(find(V>Vmax))=Vmax;
    V(find(V255))=255;
    slexx(find(slexx<0))=0;
    FF=[];
    for i=1:num
        YY=[];
        YY=[Y;reshape(slexx(i,:)',3,k)'];%将新聚类中心添加到瓷砖颜色库中
        D=[];
        D=Dis(X,YY,a1,a2);
        D=1./D;
        D(find(D==Inf))=0;
        D=sum(D,2);
        D=1./D;
        FF(i,1)=sum(D);
    end
    if min(FF)

 2.3 问题三分析与求解

第三问，在上一问基础上考虑成本，成本函数就按新增了多少个颜色来算，相当于说本问寻优的自变量个数m是变化的，可以在上述步骤增加一个目标函数M，即新增m个颜色。本问即是多目标寻优问题。针对问题三，在本题中，除却考虑拼接图像的表现外，研发成本也成为了在优化问题中的一个重要考虑对象。针对表现力问题，我们考虑了新聚类中心在空间中的分布，并且利用了 FCM 思想，给定了表现力函数；而成本问题，由于研发任意一中新颜色的成本相同，且与颜色本身无关，因此我们把研发成本与颜色数量认定为线性关系，并建立其成本函数。据以上所述，我们建立起以增加数目为变化的决策变量，以表现力函数和成本函数共同为目标函数的多目标优化模型，并利用了非支配排序算法与模拟退火算法，对模型进行求解。

%MATLAB自建函数
function D=distance(X,Y,a1,a2) 
    s=std(X-Y); 
    d=sqrt(sum((X-Y).^2)); 
    D=s*a1+d*a2; 
end 

function [TT,chrom]=ns2(NN,F1,F2) 
    a = 0; 
    T1 = []; 
    T2 = []; 
    chrom=NN; 
    chrom1 = []; 
    chrom2 = []; 
    while a == 0 
        M = []; 
        for i = 1:length(F1) 
            M(i,1) = length(find(F10 && b1(1) == 0 
            T1 = [T1;F1(b2(1)),F2(b2(1))]; 
            chrom1 = [chrom1;chrom(b2(1),:)]; 
            F1(b2(1)) = []; 
            F2(b2(1)) = []; 
            chrom(b2(1),:) = []; 
        else 
            a = 1; 
            T2 = [F1,F2]; 
            chrom2 = chrom;
        end 
    end 
    T2 = T2(b2,:); 
    chrom2 = chrom2(b2,:); 
    if size(T1,1) > 2 
        y = yongji(T1);%拥挤度 
        for i = 2:size(T1,1) 
            if y(i-1) > y(i) 
                T1(i-1:1:i,:) = T1(i:-1:i-1,:); 
                chrom1(i-1:1:i,:) = chrom1(i:-1:i-1,:); 
            end
        end
    end
    if length(T2) > 0
        y = yongji(T2);%拥挤度 
        for i = 2:size(T2,1) 
            if b1(i) == b1(i-1) 
                if y(i-1) > y(i) 
                    T2(i-1:1:i,:) = T2(i:-1:i-1,:); 
                    chrom2(i-1:1:i,:) = chrom2(i:-1:i-1,:); 
                end
            end
        end
    end
    TT = [T1;T2];
    chrom = [chrom1;chrom2]; 
end 
function y=yongji(H) 
    y1=H(:,1); 
    y2=H(:,2); 
    [yy1,a1]=sort(y1); 
    [yy2,a2]=sort(y2); 
    L=[]; 
    L=[1 1]; 
    for i=2:length(yy1)-1 
        L=[L;(yy1(i+1,1)-yy1(i-1,1))/(max(yy1)-min(yy1)),(yy2(i+1,1)-yy2(i-1,1))/(max(yy2) 
        32-min(yy2))]; 
    end 
    L=[L;1 1]; 
    L=[L(a1,1),L(a2,2)]; 
    y=sum(L,2); 
end 
function D=Dis(X,Y,a1,a2) 
    D=[]; 
    for i=1:size(X,1) 
        for j=1:size(Y,1) 
            D(i,j)=distance(X(i,:),Y(j,:),a1,a2); 
        end
    end
end

 三、总结

数学建模的趣味就是几乎没有正确答案，解法多种多样，没有绝对的好方法，只要自己用着舒服就OK，上述是我对于这道题的一些粗浅的看法，可能有一些忽略的因素，欢迎各位巨佬指点。

在学习中成功、在学习中进步！我们一起学习不放弃~

记得三连哦~ 你们的支持是我最大的动力！！欢迎大家阅读往期文章哈~

小编联系方式如下，欢迎各位巨佬沟通交流，代码什么的加小编私聊哦~

int[] arr=new int[]{4,8,3,2,6,5,1};
int[] index= new int[]{6,4,5,0,3,0,2,6,3,1};
String QQ = "";
    for (int i : index){
        QQ +=arr[i];
}
System.out.println("小编的QQ:" + QQ);