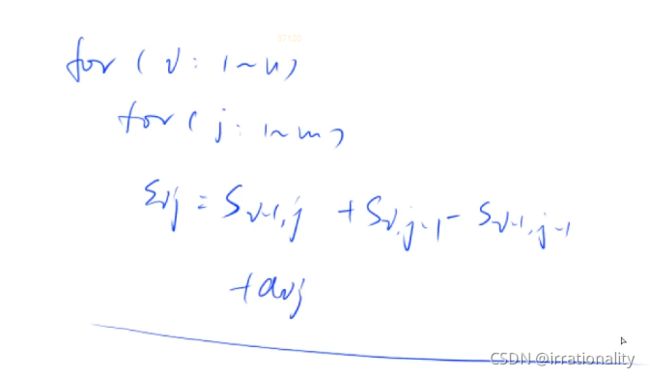基础算法（二）学习笔记

除法变成*10的减法

 前缀和的小技巧

ios : : sync_with_stdio( false);l

消时

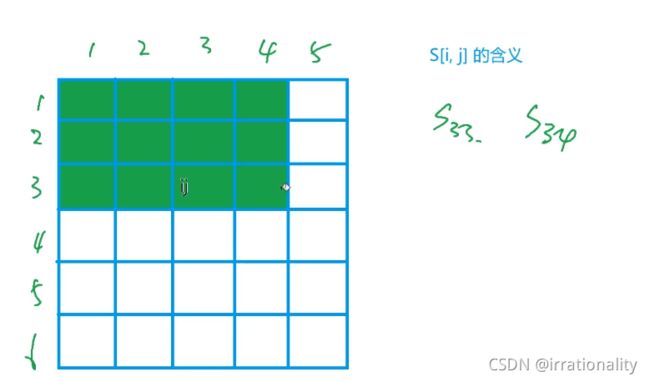
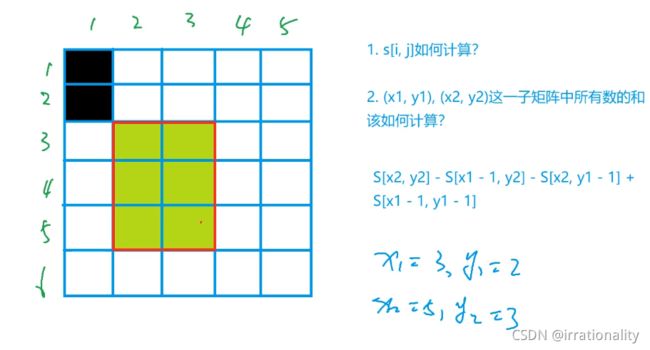
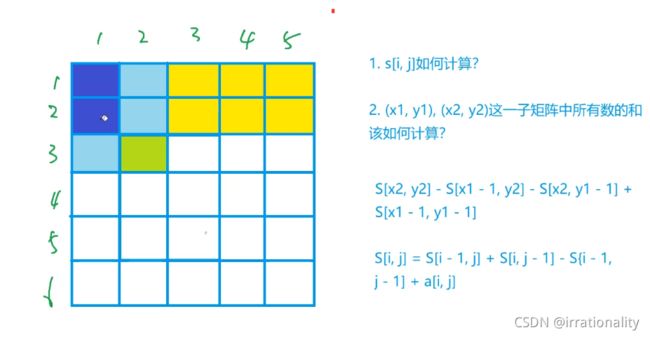
二维前缀和

 

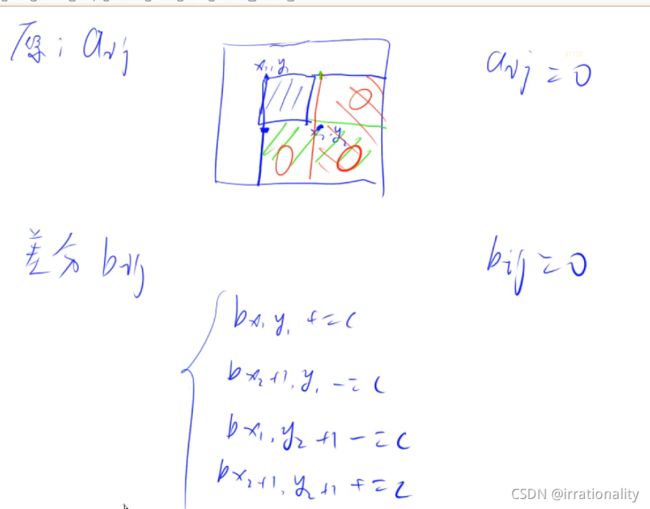
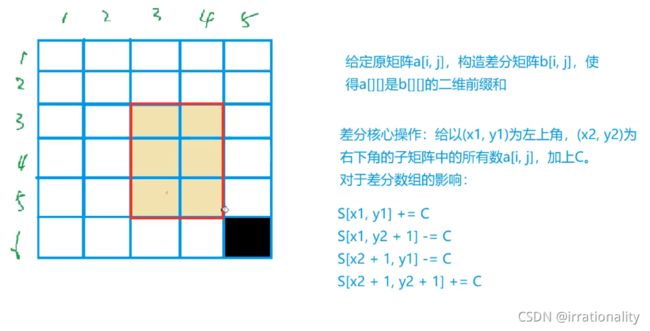
二维差分

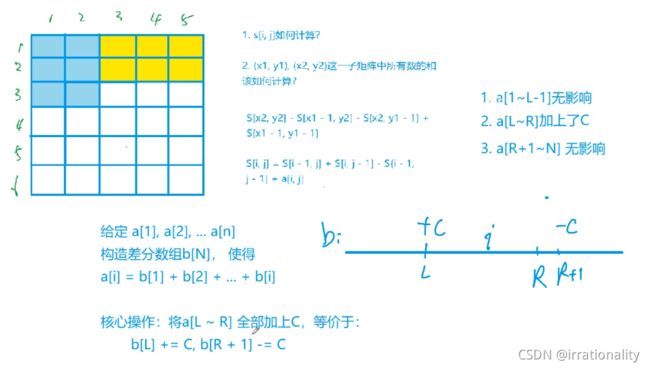
差分，O（·1·）

高精度乘法

#include 
#include 

using namespace std;


vector mul(vector &A, int b)
{
    vector C;

    int t = 0;
    for (int i = 0; i < A.size() || t; i ++ )
    {
        if (i < A.size()) t += A[i] * b;
        C.push_back(t % 10);
        t /= 10;
    }

    while (C.size() > 1 && C.back() == 0) C.pop_back();

    return C;
}


int main()
{
    string a;
    int b;

    cin >> a >> b;

    vector A;
    for (int i = a.size() - 1; i >= 0; i -- ) A.push_back(a[i] - '0');

    auto C = mul(A, b);

    for (int i = C.size() - 1; i >= 0; i -- ) printf("%d", C[i]);

    return 0;
}

//前缀和
#include 

using namespace std;

const int N = 100010;

int n, m;
int a[N], s[N];

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);

    for (int i = 1; i <= n; i ++ ) s[i] = s[i - 1] + a[i]; // 前缀和的初始化

    while (m -- )
    {
        int l, r;
        scanf("%d%d", &l, &r);
        printf("%d\n", s[r] - s[l - 1]); // 区间和的计算
    }

    return 0;
}

//高精度除法
#include 
#include 
#include 

using namespace std;

vector div(vector &A, int b, int &r)
{
    vector C;
    r = 0;
    for (int i = A.size() - 1; i >= 0; i -- )
    {
        r = r * 10 + A[i];
        C.push_back(r / b);
        r %= b;
    }
    reverse(C.begin(), C.end());
    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

int main()
{
    string a;
    vector A;

    int B;
    cin >> a >> B;
    for (int i = a.size() - 1; i >= 0; i -- ) A.push_back(a[i] - '0');

    int r;
    auto C = div(A, B, r);

    for (int i = C.size() - 1; i >= 0; i -- ) cout << C[i];

    cout << endl << r << endl;

    return 0;
}

//子矩阵的和
#include 

using namespace std;

const int N = 1010;

int n, m, q;
int s[N][N];

int main()
{
    scanf("%d%d%d", &n, &m, &q);

    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            scanf("%d", &s[i][j]);

    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];

    while (q -- )
    {
        int x1, y1, x2, y2;
        scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
        printf("%d\n", s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]);
    }

    return 0;
}

//差分
#include 

using namespace std;

const int N = 100010;

int n, m;
int a[N], b[N];

void insert(int l, int r, int c)
{
    b[l] += c;
    b[r + 1] -= c;
}

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);

    for (int i = 1; i <= n; i ++ ) insert(i, i, a[i]);

    while (m -- )
    {
        int l, r, c;
        scanf("%d%d%d", &l, &r, &c);
        insert(l, r, c);
    }

    for (int i = 1; i <= n; i ++ ) b[i] += b[i - 1];

    for (int i = 1; i <= n; i ++ ) printf("%d ", b[i]);

    return 0;
}

//差分矩阵
#include 

using namespace std;

const int N = 1010;

int n, m, q;
int a[N][N], b[N][N];

void insert(int x1, int y1, int x2, int y2, int c)
{
    b[x1][y1] += c;
    b[x2 + 1][y1] -= c;
    b[x1][y2 + 1] -= c;
    b[x2 + 1][y2 + 1] += c;
}

int main()
{
    scanf("%d%d%d", &n, &m, &q);

    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            scanf("%d", &a[i][j]);

    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            insert(i, j, i, j, a[i][j]);

    while (q -- )
    {
        int x1, y1, x2, y2, c;
        cin >> x1 >> y1 >> x2 >> y2 >> c;
        insert(x1, y1, x2, y2, c);
    }

    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];

    for (int i = 1; i <= n; i ++ )
    {
        for (int j = 1; j <= m; j ++ ) printf("%d ", b[i][j]);
        puts("");
    }

    return 0;
}

//最长连续不重复子序列
#include 

using namespace std;

const int N = 100010;

int n;
int q[N], s[N];

int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n; i ++ ) scanf("%d", &q[i]);

    int res = 0;
    for (int i = 0, j = 0; i < n; i ++ )
    {
        s[q[i]] ++ ;
        while (j < i && s[q[i]] > 1) s[q[j ++ ]] -- ;
        res = max(res, i - j + 1);
    }

    cout << res << endl;

    return 0;
}

//数组元素的目标和
#include 

using namespace std;

const int N = 1e5 + 10;

int n, m, x;
int a[N], b[N];

int main()
{
    scanf("%d%d%d", &n, &m, &x);
    for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]);
    for (int i = 0; i < m; i ++ ) scanf("%d", &b[i]);

    for (int i = 0, j = m - 1; i < n; i ++ )
    {
        while (j >= 0 && a[i] + b[j] > x) j -- ;
        if (j >= 0 && a[i] + b[j] == x) cout << i << ' ' << j << endl;
    }

    return 0;
}

//二进制中1的个数
#include 

using namespace std;

int main()
{
    int n;
    scanf("%d", &n);
    while (n -- )
    {
        int x, s = 0;
        scanf("%d", &x);

        for (int i = x; i; i -= i & -i) s ++ ;

        printf("%d ", s);
    }

    return 0;
}

//区间和
#include 
#include 
#include 

using namespace std;

typedef pair PII;

const int N = 300010;

int n, m;
int a[N], s[N];

vector alls;
vector add, query;

int find(int x)
{
    int l = 0, r = alls.size() - 1;
    while (l < r)
    {
        int mid = l + r >> 1;
        if (alls[mid] >= x) r = mid;
        else l = mid + 1;
    }
    return r + 1;
}

vector::iterator unique(vector &a)
{
    int j = 0;
    for (int i = 0; i < a.size(); i ++ )
        if (!i || a[i] != a[i - 1])
            a[j ++ ] = a[i];
    // a[0] ~ a[j - 1] 所有a中不重复的数

    return a.begin() + j;
}

int main()
{
    cin >> n >> m;
    for (int i = 0; i < n; i ++ )
    {
        int x, c;
        cin >> x >> c;
        add.push_back({x, c});

        alls.push_back(x);
    }

    for (int i = 0; i < m; i ++ )
    {
        int l, r;
        cin >> l >> r;
        query.push_back({l, r});

        alls.push_back(l);
        alls.push_back(r);
    }

    // 去重
    sort(alls.begin(), alls.end());
    alls.erase(unique(alls), alls.end());

    // 处理插入
    for (auto item : add)
    {
        int x = find(item.first);
        a[x] += item.second;
    }

    // 预处理前缀和
    for (int i = 1; i <= alls.size(); i ++ ) s[i] = s[i - 1] + a[i];

    // 处理询问
    for (auto item : query)
    {
        int l = find(item.first), r = find(item.second);
        cout << s[r] - s[l - 1] << endl;
    }

    return 0;
}

#include 
#include 
#include 

using namespace std;

typedef pair PII;

void merge(vector &segs)
{
    vector res;

    sort(segs.begin(), segs.end());

    int st = -2e9, ed = -2e9;
    for (auto seg : segs)
        if (ed < seg.first)
        {
            if (st != -2e9) res.push_back({st, ed});
            st = seg.first, ed = seg.second;
        }
        else ed = max(ed, seg.second);

    if (st != -2e9) res.push_back({st, ed});

    segs = res;
}

int main()
{
    int n;
    scanf("%d", &n);

    vector segs;
    for (int i = 0; i < n; i ++ )
    {
        int l, r;
        scanf("%d%d", &l, &r);
        segs.push_back({l, r});
    }

    merge(segs);

    cout << segs.size() << endl;

    return 0;
}

 

 

 

 

 

 

解题卡片：

1、二分法关键在于不陷入死循环，找到一个最适合点，对左右径行递归，同时避免死循环

2、快速排序关键与双指针有关，不断地减少逆序

3、归并排序除了快、稳定，而且还可以求逆序对：

        归并排序:
        1.[L，R]=> [L, mid], [mid + 1,R]

        2.递归排序[L, mid]和[mid + 1,R]

        3.归并，将左右两个有序序列合并成一个有序序列

具体而言，归并如何求出逆序对？

首先，归并是将数据不断的划分，直到最小，然后将最小的那部分不断地合并，而左边的没有用，先用的右边的那一块进行归并，那么就会产生逆序对！

总而言之，思考要往人类能够理解的方向上靠，否则还是会对身心造成伤害、、、

4、对于浮点数的二分法，也就是用牛顿法，二分法去做就好了

5、qi大于qj,那么qi后的数都与qj逆序（逆序对）

6、运行小程序，python和js都很快，因为不需要编译；而C++和java是需要编译的。

7、一维差分需要二重，二维差分需要四重，三维差分需要八重。

有问题可以留言探讨~~