机器学习算法 06 —— 聚类算法(k-means、算法优化、特征降维、主成分分析PCA)
文章目录
- 系列文章
- 聚类算法
- 1 聚类算法简介
- 2 聚类算法API初步使用
- 3 聚类算法实现流程
- 4 聚类模型评估
-
- 4.1 误差平方和(SSE)
- 4.2 肘方法
- 4.3 轮廓系数法
- 4.4 CH系数
- 4.5 小结
- 5 算法优化
-
- 5.1 Canopy算法
- 5.2 K-means++
- 5.3 二分K-means
- 5.4 K-medoids(K-中心聚类算法)
- 5.5 Kernel K-means、ISODATA、(了解)
- 6 特征工程-特征降维
-
- 6.1 什么是特征降维
- 6.2 特征选择
-
- 低方差特征过滤
- 皮尔逊相关系数
- 斯皮尔曼相关系数
- 6.3 主成分分析(PCA)
- 7 案例:探究用户对物品类别的喜好细分
系列文章
机器学习算法 01 —— K-近邻算法(数据集划分、归一化、标准化)
机器学习算法 02 —— 线性回归算法(正规方程、梯度下降、模型保存)
机器学习算法 03 —— 逻辑回归算法(精确率和召回率、ROC曲线和AUC指标、过采样和欠采样)
机器学习算法 04 —— 决策树(ID3、C4.5、CART,剪枝,特征提取,回归决策树)
机器学习算法 05 —— 集成学习(Bagging、随机森林、Boosting、AdaBost、GBDT)
机器学习算法 06 —— 聚类算法(k-means、算法优化、特征降维、主成分分析PCA)
机器学习算法 07 —— 朴素贝叶斯算法(拉普拉斯平滑系数、商品评论情感分析案例)
机器学习算法 08 —— 支持向量机SVM算法(核函数、手写数字识别案例)
机器学习算法 09 —— EM算法(马尔科夫算法HMM前置学习,EM用硬币案例进行说明)
机器学习算法 10 —— HMM模型(马尔科夫链、前向后向算法、维特比算法解码、hmmlearn)
聚类算法
学习目标:
- 掌握聚类算法实现过程
- 知道K-means算法原理
- 知道聚类算法中的评估模型
- 说明K-means的优缺点
- 了解聚类中的算法优化⽅式
- 知道特征降维的实现过程
- 应⽤Kmeans实现聚类任务
1 聚类算法简介
聚类算法是一种典型的无监督学习算法(输入只有特征值,没有目标值,没有确定的结果),主要用于将相似的样本自动归类到一个类别中。【聚类算法是⽆监督的学习算法,⽽分类算法属于监督的学习算法。】
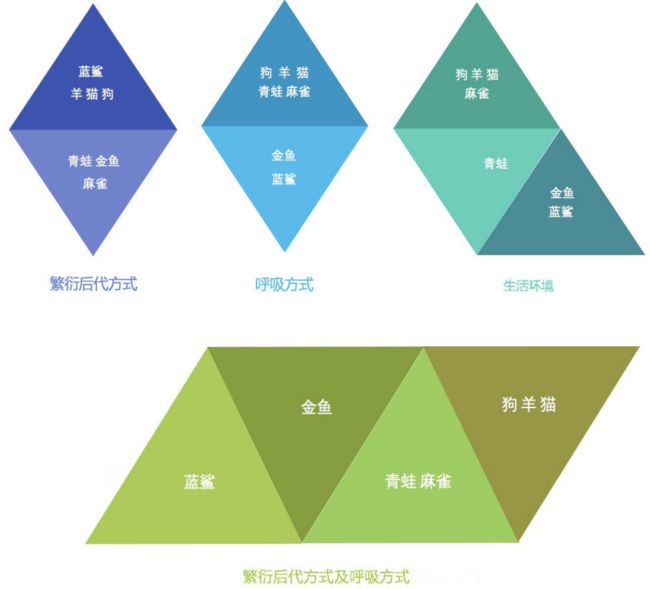
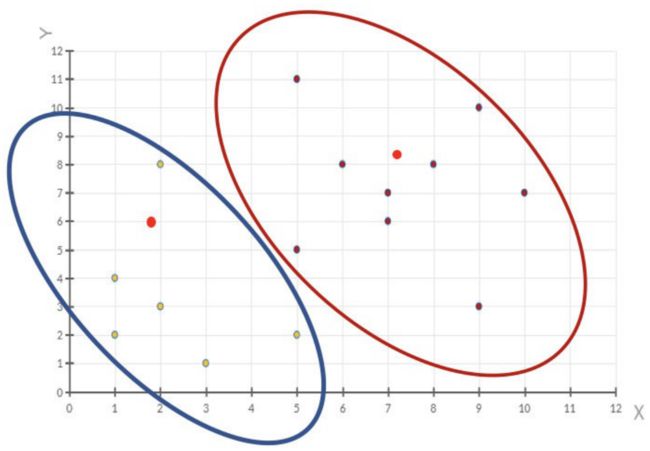
在聚类算法中根据样本之间的相似性,将样本划分到不同的类别中,对于不同的相似度计算⽅法,会得到不同的聚类结果,就像下图,常⽤的相似度计算⽅法有欧式距离法。
聚类算法在现实中的应用:
- 用户画像、广告推荐、搜索引擎的浏览推荐、恶意流量识别
- 基于位置信息的商业推送、新闻聚类、筛选排序
- 图像分割,降维,识别、离群点检测、信用卡异常消费、发掘相同功能的基因片段…
聚类算法分为细聚类和粗聚类。

2 聚类算法API初步使用
sklearn.cluster.KMeans(n_clusters=8)
- n_clusters:聚类中心数量(也称为质心数,就是要分几个类)
- 其返回的对象可以使用
fit_predict(x),它其实就是先调用fit(),然后调用predict(),因为聚类API不需要输入目标值,所以fit_predict()要简便点。
下面简单举例,通过sklearn.datasets的make_blobs方法来创建样本,然后进行分类,再通过sklearn.metrics.calinski_harabasz_score评估。
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
from sklearn.metrics import calinski_harabasz_score
# 创建数据集
# X为样本特征,y为样本簇类别。创建1000个样本,每个样本2个特征,共4个簇(因为有四个簇中心点,所以就有四个簇)。
X, y = make_blobs(n_samples=1000,
n_features=2,
centers=[[-1,1],[0,0],[1,1],[2,2], [3,3]], # 每个簇的中心点
cluster_std=[0.4,0.2,0.2,0.2, 0.3], # 每个簇的方差
random_state=9)
# 图像化展示
# 创建画布
fig = plt.figure(figsize=(10, 5), dpi=100)
ax1 = fig.add_subplot(211)
ax1.scatter(X[:, 0], X[:, 1])
# 使用K-means进行聚类-2类
# 创建估计器
estimator = KMeans(n_clusters=2, random_state=9)
# 开始训练并得到预测值
y_pre1 = estimator.fit_predict(X)
# 图像化展示
ax2 = fig.add_subplot(223)
ax2.scatter(X[:, 0], X[:, 1], c=y_pre1)
# 用Calinski-Harabasz 评估聚类情况(越大越好)
print("分2类:", calinski_harabasz_score(X, y_pre1))
# 使用K-means进行聚类-5类
# 创建估计器
estimator = KMeans(n_clusters=5, random_state=9)
# 开始训练并得到预测值
y_pre2 = estimator.fit_predict(X)
# 图像化展示
ax3 = fig.add_subplot(224)
ax3.scatter(X[:, 0], X[:, 1], c=y_pre2)
# 用Calinski-Harabasz 评估聚类情况(越大越好)
print("分5类:", calinski_harabasz_score(X, y_pre2))
plt.show()

3 聚类算法实现流程
k-means的含义:
- K : 初始中⼼点个数(计划聚类数)
- means:求中⼼点到其他数据点距离的平均值
算法具体流程:
- 随机设置K个特征空间内的点作为初始的聚类中⼼
- 对于其他每个点计算到K个中⼼的距离,接着其他点选择最近的⼀个聚类中⼼点作为自己的标记类别
- 之后重新计算出每个聚类的新中⼼点(把每个点的X加起来取平均值就是新中心点的X,Y同理)
- 如果计算得出的新中⼼点与原中⼼点⼀样(质⼼不再移动),那么结束,否则重新进⾏第⼆步过程
由于每次都要计算所有的样本与每⼀个质⼼之间的相似度,故在⼤规模的数据集上,K-Means算法的收敛速度⽐较慢。
通过图示解释:
1、假设K=3,先随机选出3个中心点。下图的蓝色、红色、绿色圆圈。
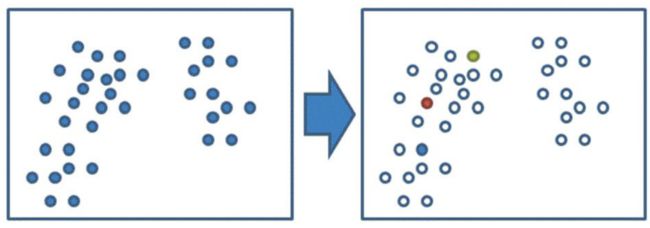
2、计算其他每个点分别到这3个中心点的距离,并根据距离自己最近的点把自己分类。例如下图那个点,距离红色最近,所以分类到红色。

3、接着计算每个聚类(簇)的新中心点,重新计算出每个聚类的新中⼼点(把每个点的X加起来取平均值就是新中心点的X,Y同理)。

4、如果计算得出的新中⼼点与原中⼼点⼀样(质⼼不再移动),那么结束,否则重新进⾏第⼆步过程 。
下面用一个案例进行说明,现在有点P1-P15,对它们进行聚类算法。

1、随机设置K个特征空间内的点作为初始的聚类中⼼(本案例中为设置p1和p2)
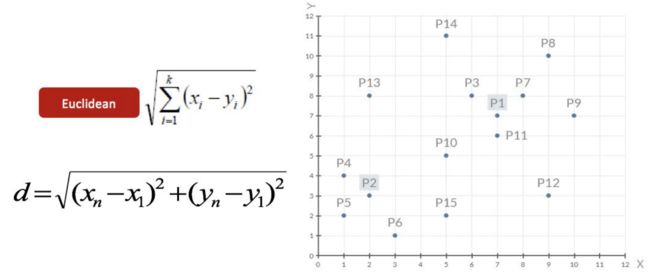
2、对于其他每个点计算到K个中⼼的距离,接着其他点选择最近的⼀个聚类中⼼点作为自己的标记类别

3、接着重新计算出每个聚类的新中⼼点(把每个点的X加起来取平均值就是新中心点的X,Y同理)

4、如果计算得出的新中⼼点与原中⼼点⼀样(质⼼不再移动),那么结束,否则重新进⾏第⼆步过程【经过判断,需要重复上述步骤,开始新⼀轮迭代】

5、当每次迭代结果不变时,认为算法收敛,聚类完成,K-Means⼀定会停下,不可能陷⼊⼀直选质⼼的过程。
4 聚类模型评估
4.1 误差平方和(SSE)
误差平方和(The sum of squares due to error)真实值和误差值的差的平方在求整体和。
例如下图:数据-0.2、0.4、-0.8、1.3、-0.7均为真实值和误差值的差。

SSE在K-Mean是中的应用是:
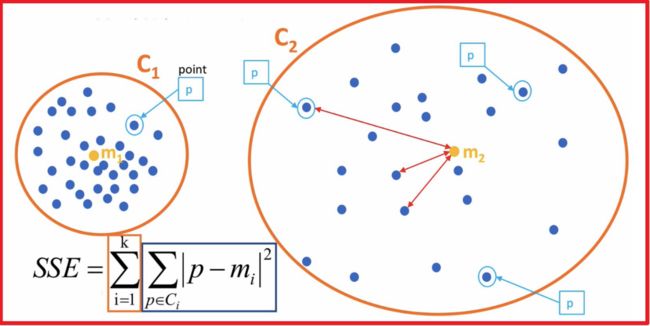
S S E = ∑ i = 1 k ∑ p ∈ C i ∣ p − m i ∣ 2 SSE=\sum\limits_{i=1}^k \sum\limits_{p \in C_i} |p-m_i|^2 SSE=i=1∑kp∈Ci∑∣p−mi∣2
用一幅图来说明。下图中K=2, C i C_i Ci是指一个区域内的所有点,p是指区域内各个点, m i m_i mi是指一个区域内所有点的平均值(X和Y分别算平均值),所有 ∣ p − m i ∣ 2 |p-m_i|^2 ∣p−mi∣2就是一个区域的SSE,而 ∑ i = 1 k \sum\limits_{i=1}^k i=1∑k是所有区域的SSE求和。SSE是松散度的衡量,所以SSE越小越好。下图中,左边区域的SSE小于右边,所以左边更好。
SSE随着聚类迭代,其值会越来越小,直到最后区域稳定。(右侧折线图的X轴是聚类整体迭代的次数)
不过,由于初始的中心点是随机选的,如果没选好可能SSE只会达到一个不太好的局部最优解。
4.2 肘方法
肘方法(Elbow method)是用来确定K值的,也就是看分成几个类别。
每次聚类完成后计算每个点到其所属簇的中⼼点的距离平⽅和,在这个平⽅和变化过程中,会出现⼀个拐点也即“肘”点,下降率突然变缓时即认为是最佳的k值。
在决定什么时候停⽌训练时,肘形判据同样有效,数据通常有更多的噪⾳,在增加分类⽆法带来更多回报时,我们停⽌增加类别。

4.3 轮廓系数法
**轮廓系数法(Silhoutte Coefficient)**结合了聚类的凝聚度(Cohesion)和分离度(Separation),⽤于评估聚类的效果:
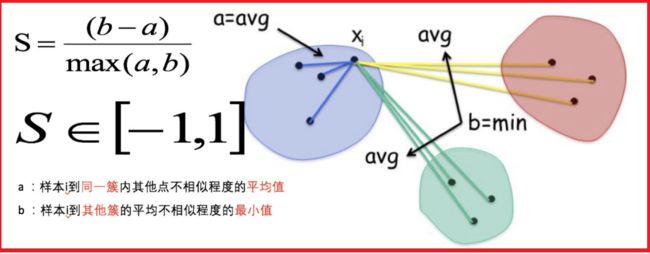
a:簇内距离。同一簇内,其他点到某个点(例如 X i X_i Xi)的距离的平均值
b:簇间距离。例如,先计算 X i X_i Xi到其他簇(例如红色)每个点的距离的平均值,再计算到绿色簇每个点的距离平均值,然后选最小的一个。
假设b远远大于a,那么SC就等于1。假设a远大于b,那么SC等于-1。
最终目的是为了追求内部距离最小化,外部距离最大化(这样分类更明显,效果就更好)。所以SC越靠近1,说明b越大于a,即外部距离大,内部距离小,说明分类越好。
然而,当我们根据不同的K计算出几个SC值差不多时,并不是盲目选更大的SC。
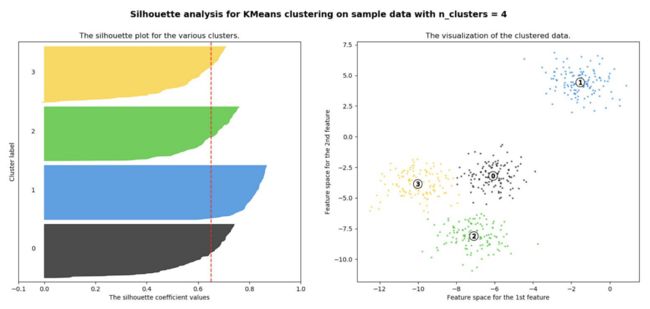
下图是500个样本含有2个feature的数据分布情况,我们对它进⾏SC系数效果衡量:

n_clusters = 2 SC : 0.7049
n_clusters = 3,SC : 0.5882
n_clusters = 4,SC : 0.6505
n_clusters = 5,SC : 0.5637
n_clusters = 6,SC: 0.4504
每次聚类后,每个样本都会得到⼀个轮廓系数,当它为1时,说明这个点与周围簇距离较远,结果⾮常好,当它为0,说明这个点可能处在两个簇的边界上,当值为负时,暗含该点可能被误分了。
从上面结果来说,K取2和4其实都不错,但我们可以从下图中看出,k取2的话,第0簇的宽度远宽于第1簇(也就是说黑色数量比绿色多太多),而k取4的话,每个簇其差别不打。所以选K=4更好。

4.4 CH系数
CH系数(Calinski-Harabasz Index):类别内部数据的协⽅差越⼩越好,类别之间的协⽅差越⼤越好,这样的Calinski-Harabasz分数s会⾼,分数s⾼则聚类效果越好。
换句话说:类别内部数据的距离平⽅和越⼩越好,类别之间的距离平⽅和越⼤越好
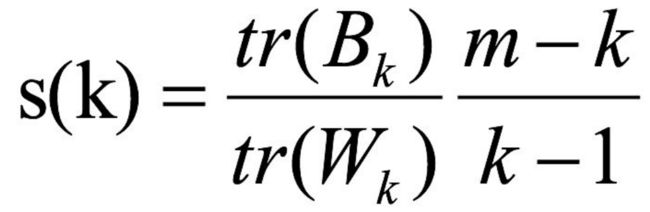
其中,tr为矩阵的迹, B k B_k Bk是类别之间的协方差矩阵, W k W_k Wk是类别内部数据的协方差矩阵,m是训练集样本数量,k是类别数量。
迹是线性代数里矩阵的的斜对角线。因为矩阵的斜对角线可以表示一个物体的相似性。而在机器学习⾥,任何⼀个矩阵计算出来之后,只要获取矩阵的迹,都可以进行简化。用迹来表示这⼀块数据最重要的特征,这样就可以把很多⽆关紧要的数据删除掉,从而简化数据,提⾼处理速度。

CH需要达到的⽬的: ⽤尽量少的类别聚类尽量多的样本,同时获得较好的聚类效果。
4.5 小结
-
SSE:误差平⽅和的值越⼩越好。
-
肘部法:下降率突然变缓时即认为是最佳的k值。
-
SC系数:取值为[-1, 1],其值越⼤越好。
-
CH系数:分数S⾼则聚类效果越好。CH需要达到的⽬的:⽤尽量少的类别聚类尽量多的样本,同时获得较好的聚类效果。
5 算法优化
k-means优缺点
优点:
-
原理简单(靠近中⼼点),实现容易
-
聚类效果中上(依赖K的选择)
-
空间复杂度o(N),时间复杂度o(KIN)。N为样本点个数,K为中⼼点个数,I为迭代次数。
缺点:
-
对离群点,噪声敏感 (中⼼点易偏移)
-
难以发现⼤⼩差别很⼤的簇及进⾏增量计算
-
结果不⼀定是全局最优,只能保证局部最优(与K的个数及初值选取有关)
5.1 Canopy算法
算法流程:
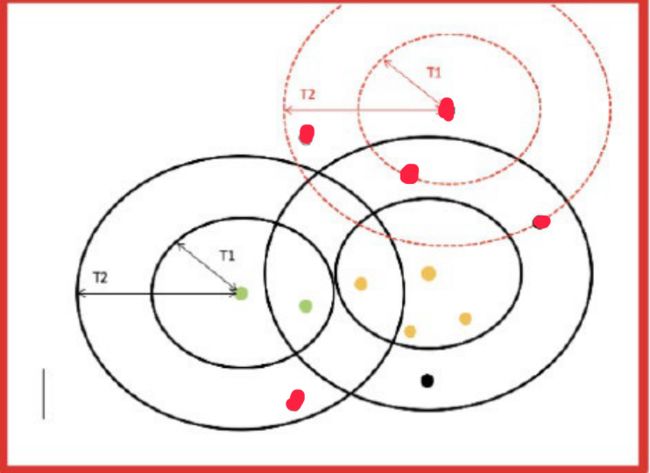
1、随机选择一个点作为中心点(黄色点)
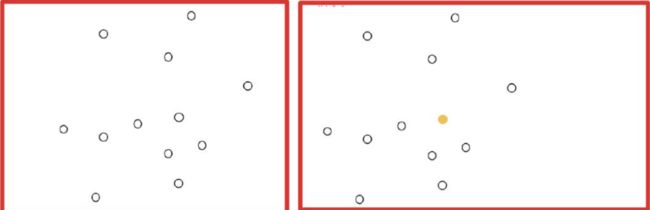
2、以当前中心点为圆心,T1为半径,形成一个圆。圆内就被划分到黄色类别。再以T2为半径,形成一个圆环,环里也归为黄色类别,但由于后面还可以被归为其他类别,所以用黑色区分。
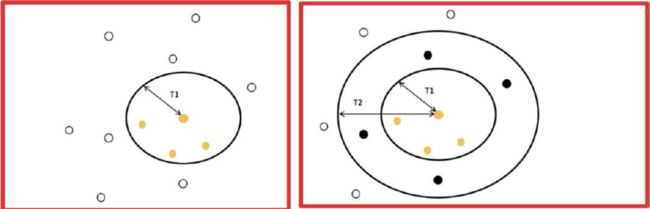
3、从T2外面找一个点作为新的中心点(绿色),然后继续以T1为半径,新中心点为圆心,画圆。此时,在新圆T1半径内的点被划分为新一类别(绿色),之前属于第一个圆里的黑色点也被归类绿色。然后,对新圆以T2为半径,做圆环,把环内的点归为绿色,但不能抢占之前圆T1半径里黄色的点。
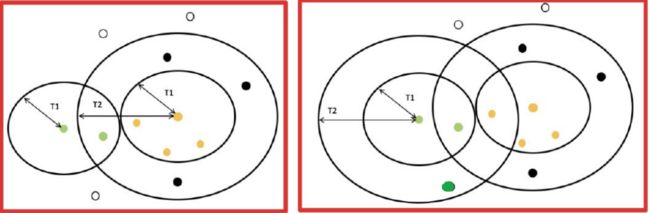
4、 继续上面步骤,直到把所有点都包含完。最终得到3个中心点,分为了3个类别。
Canopy优点:
-
K-means对噪声抗⼲扰较弱,而Canopy可以将较⼩的点的分类直接去掉,有利于抗⼲扰。
-
Canopy选择出来的每个中心点 会更精确。
-
只针对每个Canopy内部做K-means聚类,可以减少相似计算的数量。
Canopy缺点:算法中 T1、T2的确定问题 ,依旧可能落⼊局部最优解
5.2 K-means++
K-means++的目的是让所选择的每个中心点尽可能分散,它主要是用一个概率公式来选择中心点:
P = D ( x ) 2 ∑ x ∈ X D ( X ) 2 P=\frac{D(x)^2}{\sum\limits_{x \in X} D(X)^2} P=x∈X∑D(X)2D(x)2
分母 ∑ x ∈ X D ( X ) 2 \sum\limits_{x \in X} D(X)^2 x∈X∑D(X)2表示中心到其他所有点的距离的平方和,分子 D ( x ) 2 D(x)^2 D(x)2点x到中心点的距离的平方和。
例如,现在下图的中心点是2,计算点1的概率如下。(当然,真实情况下不会是这种一维坐标系)

分 母 : ∑ x ∈ X D ( X ) 2 = ( 2 − 0 ) 2 + ( 2 − 1 ) 2 + ( 2 − 3 ) 2 + . . . + ( 2 − 15 ) 2 = A 分 子 : D ( x ) 2 = ( 2 − 1 ) 2 = 1 P ( 2 _ 1 ) = 1 A 分母:\sum\limits_{x \in X} D(X)^2=(2-0)^2+(2-1)^2+(2-3)^2+...+(2-15)^2=A\\ 分子:D(x)^2=(2-1)^2=1\\ P(2\_1)=\frac{1}{A} 分母:x∈X∑D(X)2=(2−0)2+(2−1)2+(2−3)2+...+(2−15)2=A分子:D(x)2=(2−1)2=1P(2_1)=A1
然后选择概率最大的那个点作为第二个中心点,接着又对新的中心点进行计算。
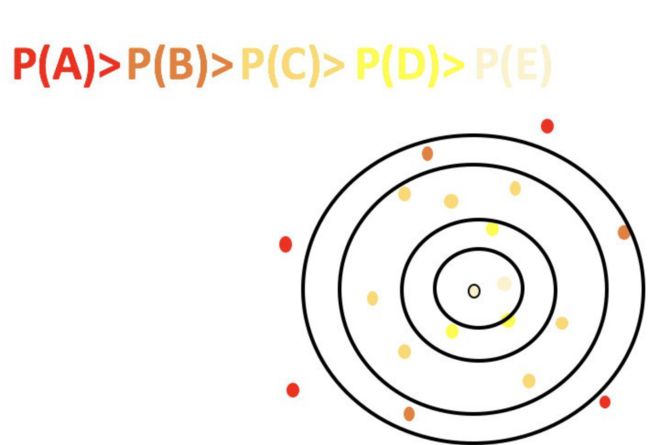
如下图中,假如第⼀个中心点是在圆⼼,那么选择的第二个最优中心点就会在P(A)这个区域【根据颜⾊进⾏划分,A是最外层】,因为距离最远,这也符合K-means++尽可能选择分散点作为中心点的目的。
5.3 二分K-means
先看流程,然后进行说明。
1、所有点作为⼀个簇,将该簇⼀分为⼆,并计算每个簇的聚类代价函数(也就是误差平方和)

2、选择能最⼤限度降低聚类代价函数的簇,并将其再划分为两个簇。

3、一直持续这样划分,直到簇的数目满足用户给定的K值。
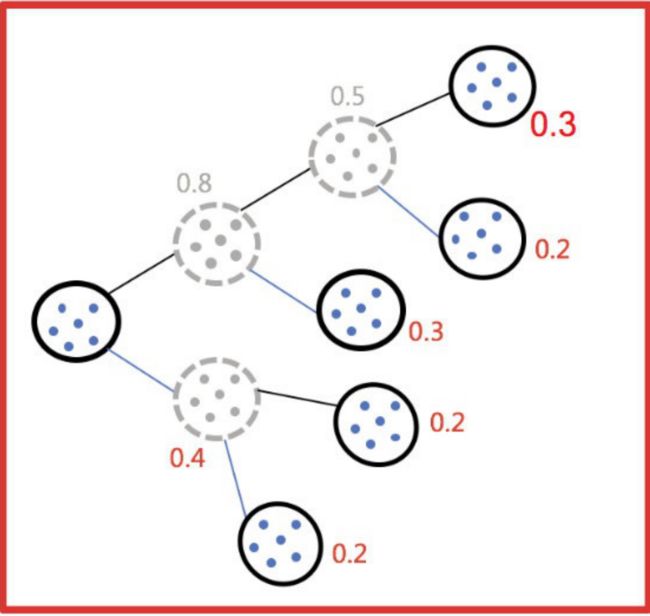
因为聚类的误差平⽅和能够衡量聚类性能,该值越⼩表示数据点越接近于他们的质⼼,聚类效果就越好,所以需要对误差平⽅和最⼤的簇进⾏再⼀次划分。误差平⽅和越⼤,表示该簇聚类效果越不好,越有可能是多个簇被当成了⼀个簇,从而我们⾸先需要对这个簇进⾏划分。
⼆分K均值算法可以加速K-means算法的执⾏速度,因为它的相似度计算少了并且不受初始化问题的影响,这⾥不存在随机点的选取,且每⼀步都保证了误差最⼩。
5.4 K-medoids(K-中心聚类算法)
K-medoids和K-means是有区别的,不⼀样的地⽅在于中⼼点的选取
- K-means中,中⼼点取为当前簇中所有数据点的平均值【所以会对异常点很敏感】
- K-medoids中,从当前簇里选取到其他所有(当前簇中的)点的距离之和最⼩的点作为中⼼点

算法流程
1、总体n个样本点中任意选取k个点作为medoids。
2、按照与medoids最近的原则,将剩余的n-k个点分配到当前最佳的medoids代表的类中。
3、对于第i个类中除对应medoids点外的所有其他点,按顺序计算当其为新的medoids时,代价函数的值,遍历所有可能,选取代价函数最⼩时对应的点作为新的medoids。
4、重复2-3的过程,直到所有的medoids点不再发⽣变化或已达到设定的最⼤迭代次数。
5、产出最终确定的k个类。
k-medoids的鲁棒性(稳定性)更好。
简单举个例。假如现在有(1, 1) (1, 2) (2, 1) (1000, 1000)四个点,显然(1000, 1000)是个异常点。
如果按照k-means的方法来确定中心点,由于是按所有数据点的平均值,所有中心点大概会在(500, 500)左右。然而这个中心点距离前三个点和最后一个点都比较远,明显中心点取得不太好。
如果按照k-medoids的方法就会计算各个距离,(1, 1)到另外三个点的距离,(1, 2)到另外三个点的距离,(2, 1)到另外三个点的距离,(1000, 1000)到另外三个点的距离,此时就会发现(1000, 1000)到另外点的距离很大,就会排除掉,因为是找代价函数最小的点。
k-medoids只能对⼩样本起作⽤,样本⼤,速度就会很慢。同时,当样本多的时候,少数⼏个噪⾳对k-means的质⼼影响也没有想象中的那么重,所以k-means的应⽤还是⽐k-medoids多。
5.5 Kernel K-means、ISODATA、(了解)
kernel k-means
实际上,就是将每个样本进⾏⼀个投射到⾼维空间的处理,然后再将处理后的数据使⽤普通的k-means算法思想进⾏聚类。

ISODATA
类别数⽬K随着聚类过程⽽变化,对类别数会进⾏合并,分裂。(也就是会动态改变K值)
“合并”:(当聚类结果某⼀类中样本数太少,或两个类间的距离太近时)
“分裂”:(当聚类结果中某⼀类的类内⽅差太⼤,将该类进⾏分裂)
Mini Batch K-Means
适合⼤数据的聚类算法。⼤数据量是什么量级?通常当样本量⼤于1万做聚类时,就需要考虑选⽤Mini Batch K-Means算法。
Mini Batch K-Means使⽤了Mini Batch(分批处理)的⽅法对数据点之间的距离进⾏计算。
Mini Batch计算过程中不必使⽤所有的数据样本,⽽是从不同类别的样本中抽取⼀部分样本来代表各⾃类型进⾏计算。 由于计算样本量少,所以会相应的减少运⾏时间,但另⼀⽅⾯抽样也必然会带来准确度的下降。
该算法的迭代步骤有两步:
-
从数据集中随机抽取⼀些数据形成⼩批量,把他们分配给最近的中心点
-
更新中心点
与Kmeans相⽐,数据的更新在每⼀个⼩的样本集上。对于每⼀个⼩批量,通过计算平均值得到更新质⼼,并把⼩批量⾥的数据分配给该质⼼,随着迭代次数的增加,这些质⼼的变化是逐渐减⼩的,直到质⼼稳定或者达到指定的迭代次数,停⽌计算。
6 特征工程-特征降维
6.1 什么是特征降维
降维是指在某些限定条件下,降低随机变量**(特征)个数,得到⼀组“不相关”**主变量的过程。例如把三维坐标系降到二维,就是把xyz里的z去掉,或者是把地球仪降维成地图。
通常我们降维是选择相关性较强的特征,例如相对湿度和降雨量,二者是这个相关,那么我们可以选择去掉降雨量。
降维有两种方式:特征选择和主成分分析(可以理解为一直特征提取的方式)。
6.2 特征选择
数据中包含冗余或⽆关的变量(或者叫特征、属性),特征选择旨在从原有特征中找出主要特征。
例如下面有一只鸟,它具备一些特征。我们知道,鸟的眼睛大部分都是一颗豆子,所以其实眼睛的宽度和长度保留一个就好。
我们进行特征选择主要有过滤式和嵌入式。
Filter(过滤式):主要探究特征本身特点、特征与特征和⽬标值之间关联。
- ⽅差选择法:低⽅差特征过滤
- 相关系数:皮尔逊相关系数、
Embedded (嵌⼊式):算法⾃动选择特征(特征与⽬标值之间的关联)
- 决策树***信息熵、信息增益
- 正则化:L1、L2
- 深度学习:卷积等
低方差特征过滤
特征⽅差⼩:说明某个特征的⼤多数样本值⽐较相近
特征⽅差⼤:说明某个特征有很多样本的值都存在差别
我们需要删除方差小的特征,保留方差大的特征,这样数值接近的样本基于可以过滤掉。
1、先通过sklearn.feature_selection.VarianceThreshold(threshold = 0.0)实例化一个对象
2、用得到的对象调用fit_transform(X)来转换。
- X是numpy array格式的数据[n_samples,n_features]
- 返回值是一个删除了低于threshold的特征的X。【默认threshold=0,即删除样本中具有相同值的特征】
下面用代码演示:
可以发现,只保留了第2列。【其余三列特征方差都小于1】
data = pd.DataFrame([[0,2,0,3],
[0,1,4,3],
[0,1,1,3]])
print("过滤前的形状:", data.shape)
# 1. 实例化 转换器
transfer = VarianceThreshold(threshold=1) # 方差低于1的列就删除
# 2. 获取结果
data = transfer.fit_transform(data)
print("过滤后的形状:", data.shape)
print("保留的特征:", transfer.get_support())
皮尔逊相关系数
皮尔逊相关系数是反映变量(特征)之间相关关系密切程度的统计指标,其公式如下(无需记忆):其中x、y就是两个变量(特征),n是行数。
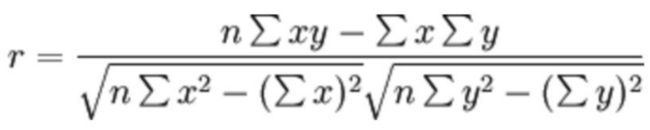
相关系数的值在区间[-1, 1]。其性质如下:
-
当r>0时,表示两变量正相关,r<0时,两变量为负相关
-
当**|r|=1时,表示两变量为完全相关,当r=0**时,表示两变量间⽆相关关系
-
当0<|r|<1时,表示两变量存在⼀定程度的相关。且**|r|越接近1**,两变量间线性关系越密切;|r|越接近于0,表示两变量的线性相关越弱
-
⼀般可按三级划分:|r|<0.4为低度相关;0.4≤|r|<0.7为显著性相关;0.7≤|r|<1为⾼度线性相关
API:from scipy.stats import pearsonr,pearsonr(x, y)其中x,y是两列特征数据。返回值是一个元祖(a, b),a就是皮尔逊相关系数r。【b是在样本数量大于500时才具有参考意义,b越接近0说明越好,通常我们只需要关注a就行】
下面举例
from scipy.stats import pearsonr
x1 = [12.5, 15.3, 23.2, 26.4, 33.5, 34.4, 39.4, 45.2, 55.4, 60.9]
x2 = [21.2, 23.9, 32.9, 34.1, 42.5, 43.2, 49.0, 52.8, 59.4, 63.5]
print("皮尔逊系数:",pearsonr(x1, x2))
斯皮尔曼相关系数
斯皮尔曼相关系数也是反映变量之间相关关系密切程度的统计指标,它公式更加简单,所以应用更加广泛,通常是用斯皮尔曼。
其公式如下(无需记忆):n为等级个数,d为⼆列成对变量的等级差数
API:from scipy.stats import pearsonr,pearsonr(x, y)其中x,y是两列特征数据。用法以及判断标准和皮尔逊一样的,只是计算方式不同。
from scipy.stats import spearmanr
x1 = [12.5, 15.3, 23.2, 26.4, 33.5, 34.4, 39.4, 45.2, 55.4, 60.9]
x2 = [21.2, 23.9, 32.9, 34.1, 42.5, 43.2, 49.0, 52.8, 59.4, 63.5]
print("斯皮尔曼相关系数:",spearmanr(x1, x2))
![]()
6.3 主成分分析(PCA)
PCA(Principal Component Analysis),即主成分分析方法,是一种使用最广泛的数据降维算法。
PCA就是用少数变量(特征)来替代原先多个变量(特征),并且将多个变量中有用的信息提取到少数几个变量中,即降维。
例如下面这张图,我们有一个茶壶的左视图、右视图、俯视图,以便得知茶壶外形。但其实我们可以将三张图合并化简为一张侧视图,这样便能以少量信息能得知茶壶的大概。当然,化简后必然还是无法得知全貌,所以有一定缺陷,同时我们之所以能合并三张图,是因为三张图本身存在一定相关性。

这里引用知乎上另一个比较形象的关于PCA的举例:如何通俗易懂地讲解什么是 PCA 主成分分析?
具体PCA是如何完成降维的,这需要用到一定的数学知识(线性代数),如果想要了解可以参考https://www.zhihu.com/question/41120789。
API:
1、先调用sklearn.decomposition.PCA(n_components=None)。其中n_components如果指定为小数,则表示保留百分之多少的信息,如果指定为整数,则表示保留多少特征数。
2、再调用fit_transform(X),X是我们传入的特征值。
下面用代码演示。
from sklearn.decomposition import PCA
# 构建数据
data = [[2, 8, 4, 5],
[6, 3, 0, 8],
[5, 4, 9, 1]]
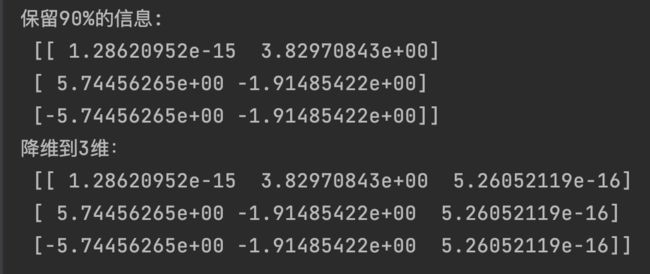
# 保留90%的信息
transfer = PCA(n_components=0.9)
print("保留90%的信息:\n", transfer.fit_transform(data))
# 降维到3维(如果选择降维到2维,那么结果会和保留90%信息相同)
transfer = PCA(n_components=3)
print("降维到3维:\n", transfer.fit_transform(data))
7 案例:探究用户对物品类别的喜好细分
这是来自Kaggle的一个竞赛题,我们应⽤pca和K-means实现⽤户对物品类别的喜好细分划分。
数据集下载:https://download.csdn.net/download/qq_39763246/21425420

-
order_products__prior.csv:订单与商品信息,字段:order_id, product_id, add_to_cart_order, reordered
-
products.csv:商品信息 ,字段:product_id, product_name, aisle_id, department_id
-
orders.csv:⽤户的订单信息 ,字段:order_id,user_id,eval_set,order_number,….
-
aisles.csv:商品所属具体物品类别 ,字段: aisle_id, aisle
1、获取数据
import pandas as pd
from sklearn.decomposition import PCA
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
# 1 获取数据
# 订单与商品信息
order_product = pd.read_csv("./data/instacart/order_products__prior.csv")
# 商品信息
products = pd.read_csv("./data/instacart/products.csv")
# 用户订单信息
orders = pd.read_csv("./data/instacart/orders.csv")
# 商品所属具体物品类别
aisles = pd.read_csv("./data/instacart/aisles.csv")
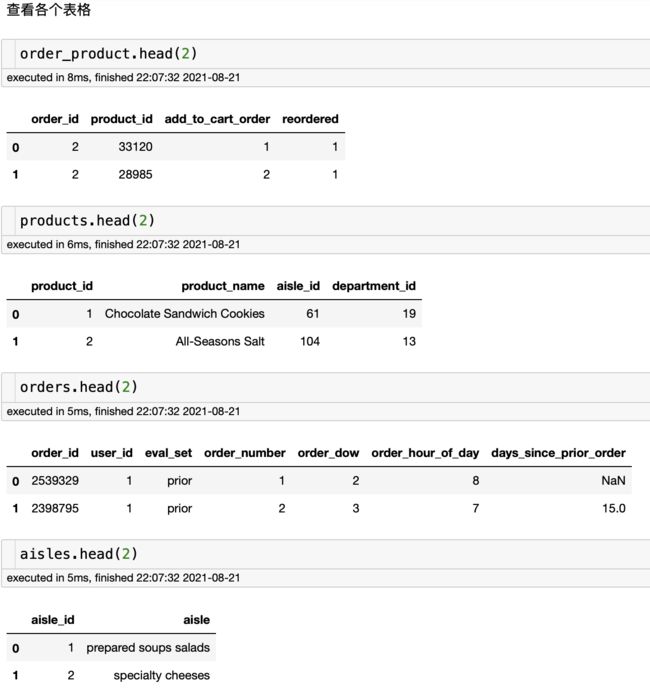
2、数据基本处理
2.1 合并表格:先将四张表合并,才好进行训练。
# 2. 数据基本处理
# 2.1 合并表格
table1 = pd.merge(order_product, products, on=["product_id", "product_id"])
table2 = pd.merge(table1, orders, on=["order_id", "order_id"])
table = pd.merge(table2, aisles, on=["aisle_id", "aisle_id"])

2.2 交叉表合并:实际上我们只需要关注用户和商品类别,所以对这两列进行交叉表合并。【交叉表在我另一篇博客里有介绍 Pandas】
# 2.2 交叉表合并
table = pd.crosstab(table["user_id"], table["aisle"])
交叉表合并后,行索引就是user_id,列索引是各个商品类别,其中每个元素就是某个user_id对于某个商品的购买数目。

2.3 数据截取
# 2.3 数据截取(考虑到数据太多,会花费很多时间,所以这里只用了部分数据,前1000行)
table = table[:1000]
3、特征工程
# 3. 特征工程 - PCA 只保留90%的数据
transfer = PCA(n_components=0.9)
data = transfer.fit_transform(table)
从134列降到了22列
4、机器学习
# 4. 机器学习 - K-means
estimator = KMeans(n_clusters=8, random_state=9)
data_predict = estimator.fit_predict(data)
5、模型评估
# 5. 模型评估 - silhouette 轮廓系数评估,越接近1越好
print("SC:", silhouette_score(data, data_predict))