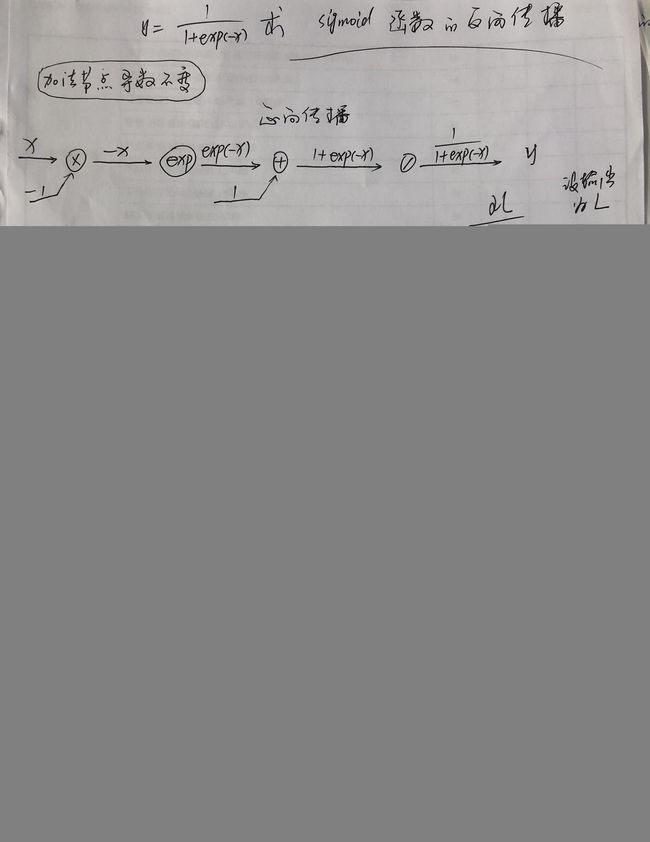
误差反向传播法【二、神经网络以层的方式实现】

我们来看激活函数层的实现，激活函数大家在刚学习神经网络的时候就有所了解，准确来说在接触感知机的时候就会出现，它是进入神经网络的入门知识。
ReLU层（Rectified Linear Unit）修正线性单元

import numpy as np
class Relu:
   def __init__(self):
       self.mask=None
   def forward(self,x):
       self.mask=(x<=0)#[[False  True][ True False]]
       out=x.copy()
       out[self.mask]=0#将True设为0
       return out
   def backward(self,dout):
       dout=(~self.mask).astype(int)
       dx=dout
       return dx
x=np.array([[1.0,-0.5],[-2.0,3.0]])
relu=Relu()
relu.forward(x)
[[ 1.  0.]
 [ 0.  3.]]
relu.backward(x)
[[ 1.  0.]
 [ 0.  1.]]

上面的正向和反向等价于下面的代码：
def relu(x):
    return np.maximum(0, x)#[[ 1.  0.][ 0.  3.]]
def relu_grad(x):
    grad=np.zeros_like(x)#zeros的参数是形状，这个需要注意
    grad[x>=0]=1
    return grad
#[[ 1.  0.][ 0.  1.]]

Sigmoid层

前面我们知道Sigmoid函数的公式：

 代码如下：

class Sigmoid:
    def __init__(self):
        self.out=None
    def forward(self,x):
        out=1/(1+np.exp(-x))
        self.out=out
        return out
    def backward(self,dout):
        dx=dout*self.out*(1.0-self.out)
        return dx
或写成下面这样的代码：
def sigmoid(x):
    return 1/(1+np.exp(-x))
def sigmoid_grad(x):
    return sigmoid(x)*(1.0-sigmoid(x))

Affine层

神经网络的正向传播中进行的矩阵的乘积运算在几何学领域叫做“放射变换”，所以将这里的处理实现为“Affine层”
乘积反向传播求导需要特别注意两点
1、除了翻转值之外还需要将翻转来的数组进行转置之后再乘积
2、乘积的顺序不要弄错了
因为乘积对数组的形状有要求，需要对应维度的元素个数保持一致，关于乘积更详细说明 :矩阵的乘法、乘积(点积）和softmax函数的溢出https://blog.csdn.net/weixin_41896770/article/details/119141707

αL/αX=αL/Y  *  W.T(W权重数组的转置)
αL/αW=X.T  *   αL/Y

下面的代码也考虑到了四维数组（张量）的处理：

import numpy as np
class Affine:
    def __init__(self,W,B):
        self.W=W
        self.B=B
        self.X=None
        #保存X的形状，针对四维数组（张量）做变形之后的还原
        self.Xshape=None
        #权重和偏置的导数
        self.dW=None
        self.dB=None
    def forward(self,X):
        self.Xshape=X.shape
        X=X.reshape(X.shape[0],-1)#转换成矩阵，比如(5,2,3,4)转成(5,24)
        self.X=X
        out=np.dot(self.X,self.W)+self.B
        return out
    def backward(self,dout):
        dX=np.dot(dout,self.W.T)
        self.dW=np.dot(self.X.T,dout)
        self.dB=np.sum(dout,axis=0)
        dX=dX.reshape(self.Xshape)#还原输入数据的形状，针对张量
        return dX

W=np.array([[0,0,0],[10,10,10]])
B=np.array([1,2,3])
affine=Affine(W,B)
X=np.array([[1,1],[2,5]])
dY=affine.forward(X)
array([[11, 12, 13],
       [51, 52, 53]])
dX=affine.backward(dY)
array([[   0,  360],
       [   0, 1560]])
affine.dW
array([[113, 116, 119],
       [266, 272, 278]])
affine.dB
array([62, 64, 66])

Softmax层（最后一层，还有一个交叉熵误差函数层）

        正向传播时若有分支流出，则反向传播时它们的反向传播的值会相加，所以大家在上面的除法运算这个节点可以看到有分支流出，那么需要求和再做除法的导数，-t1S-t2S-t3S=-(S(t1+t2+t3))=-S，因为t1,t2,t3这些是独热编码的标签，所以只有一个1，其余为0，故他们的和就是1，求-S的除法的导数，我们知道就是乘以-(1/S)²，就是1/S。从上面的这个反向传播推导图得到了一个非常漂亮的简单结果，是(y1-t1,y2-t2,y3-t3)这样的差分结果（Softmax层的输出y-监督标签t）

        有了前面的基础，我们现在来实现N层的神经网络，还是以手写数字识别为例，通过若干层的Affine层 | ReLU层的传播之后，最后经过Affine层将得到10个分类的分数（10个数字分别的打分），再通过Softmax层就可以知道每个数字识别的概率，最大的那个就是我们识别的标签
        神经网络学习的目的就是通过调整权重参数，使神经网络的输出接近监督标签。那么反向求导的代码就显得非常简单了，其中需要用到的两个函数softmax和cross_entropy_error，需要查阅的可以点击 Python随机梯度下降法（四）【完结篇】

import sys,os
import numpy as np
os.chdir('D:\Anaconda3\TONYTEST')
sys.path.append('D:\Anaconda3\TONYTEST')
from common.functions import *
from common.gradient import numerical_gradient
from collections import OrderedDict

class SoftmaxLoss:
    '''
    Softmax分类函数和交叉熵误差的损失函数
    误差反向传播求导的最后一层

    '''
    def __init__(self):
        self.loss=None
        self.y=None
        self.t=None
    def forward(self,x,t):
        self.y=softmax(x)
        self.t=t
        self.loss=cross_entropy_error(self.y,self.t)
        return self.loss
    def backward(self,dout=1):
        batchSize=self.t.shape[0]
        dx=(self.y-self.t)/batchSize
        return dx

class TwoLayerNet:
    def __init__(self,inputSize,hiddenSize,outputSize,weightStd=0.01):
        self.params={}
        self.params['W1']=weightStd*np.random.randn(inputSize,hiddenSize)
        self.params['b1']=np.zeros(hiddenSize)
        self.params['W2']=weightStd*np.random.randn(hiddenSize,outputSize)
        self.params['b2']=np.zeros(outputSize)
        #通过有序字典来保存层，反向传播的时候只需要把层的顺序反向调用即可
        self.layers=OrderedDict()
        self.layers['Affine1']=Affine(self.params['W1'],self.params['b1'])
        self.layers['Relu1']=Relu()
        self.layers['Affine2']=Affine(self.params['W2'],self.params['b2'])
        self.lastLayer=SoftmaxLoss()
    def predict(self,x):
        for layer in self.layers.values():
            x=layer.forward(x)
        return x

    def loss(self,x,t):
        y=self.predict(x)
        return self.lastLayer.forward(y,t)

    def accuracy(self,x,t):
        y=self.predict(x)
        y=np.argmax(y,axis=1)#每行最大值的索引
        if t.ndim!=1:t=np.argmax(t,axis=1)
        accu=np.sum(y==t)/float(x.shape[0])
        return accu

    def gradient(self,x,t):
        '''
        比数值微分高效的误差反向传播求导
        获取权重和偏置参数的梯度
        '''
        #forward
        self.loss(x,t)
        #backward
        dout=1
        dout=self.lastLayer.backward(dout)

        layers=list(self.layers.values())#将有序字典保存的层的值，先转换成list再进行反转
        layers.reverse()#反转
        for layer in layers:
            dout=layer.backward(dout)

        grads={}
        grads['W1'],grads['b1']=self.layers['Affine1'].dW,self.layers['Affine1'].dB
        grads['W2'],grads['b2']=self.layers['Affine2'].dW,self.layers['Affine2'].dB
        return grads

    def numerical_gradient(self,x,t):
        loss_W=lambda W:self.loss(x,t)
        grads={}
        grads['W1']=numerical_gradient(loss_W,self.params['W1'])
        grads['b1']=numerical_gradient(loss_W,self.params['b1'])
        grads['W2']=numerical_gradient(loss_W,self.params['W2'])
        grads['b2']=numerical_gradient(loss_W,self.params['b2'])
        return grads

        做完之后需要做一个梯度确认的操作，前面说过数值微分简单不容易出错，但效率低，所以一般都是拿来检测误差反向传播法是否正确的。确保数值微分求出来的梯度和误差反向传播法求出来的结果相差很小就对了，一般为0是很少见的，因为计算机存在一个精度有限的问题（如32位浮点数），受到数值精度的限制，所以一般都不会为0，只能是一个很接近于0的值

from dataset.mnist import load_mnist
(x_train,t_train),(x_test,t_test)=load_mnist(normalize=True,one_hot_label=True)
network=TwoLayerNet(inputSize=784,hiddenSize=50,outputSize=10)
x_batch=x_train[:3]#(3,784)
t_batch=t_train[:3]
grad_numerical=network.numerical_gradient(x_batch,t_batch)#数值微分求导
grad_backprop=network.gradient(x_batch,t_batch)#误差反向传播法求导
for k in grad_numerical.keys():
    diff=np.average(np.abs(grad_backprop[k]-grad_numerical[k]))#差的绝对值的平均值
    #print(grad_backprop[k].shape)#(784,50)(50,)(50,10),(10,)
    print(k+":"+str(diff))

W1:0.17803059095
b1:1.33964910075
W2:4.77057756268e-09
b2:1.40236227449e-07