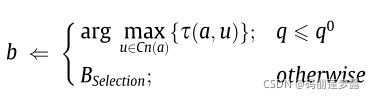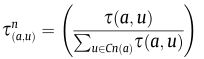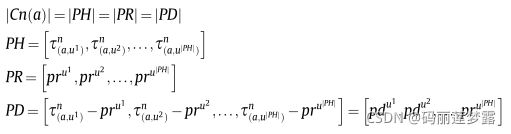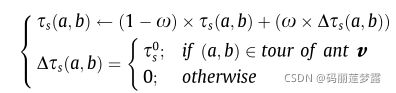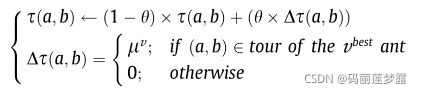cyclic job shop 机器人单元调度问题的蚁群优化(Ant colony optimization)的论文简读和python框架复现

《Cyclic job shop robotic scheduling problem:Ant colony optimization》

 

Computer & Industrial Engineering/2017

 更多车间调度及强化学习求解车间调度问题的相关代码可前往个人Github:Aihong-Sun (Sun Aihong) (github.com) 

1摘要

         本文讨论了多机器人循环作业车间机器人单元调度问题。所有作业均以标准的加工时间在多台机器上按顺序进行加工，单夹机器人执行机器之间工件的的运输操作。由于所考虑问题的特殊性和NP-hard计算复杂度，提出了一种基于蚁群优化的元启发式算法。所提出的算法同时确定循环时间表中的最佳作业高度，用于运输操作的机器人分配以及机器人移动的最佳排序，这反过来使吞吐量率最大化。通过对一组随机生成的问题实例的计算研究来检验所提出的模型的效率。

2 问题描述

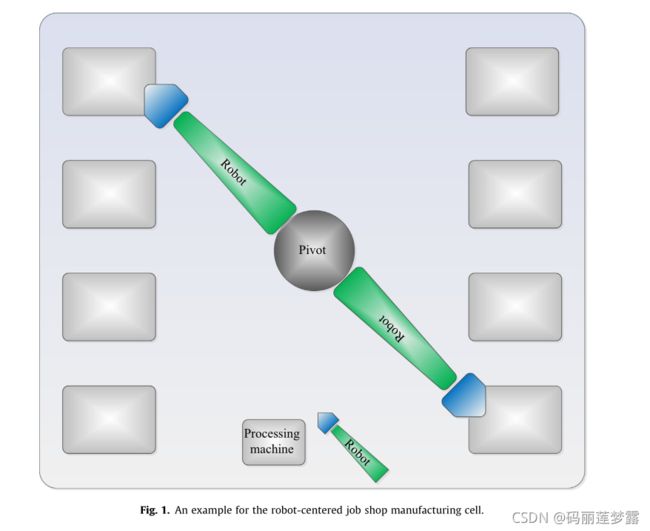
   多个单爪机器人的循环作业车间可以描述为下图所示场景：

3 MB-ACO

        CJS-RCS问题包含的子问题：分配问题、排序问题和调度问题，针对这三个问题，这篇文章提出了一种多桥蚁群优化算法(MB-ACO)来解决CJS-RCS问题，其中每个桥将代表子问题的不同区域连接成不同的节点集。子问题及其相关节点集的详细说明将在以下各节中介绍。

3.1 确定周期开始时占用的机器

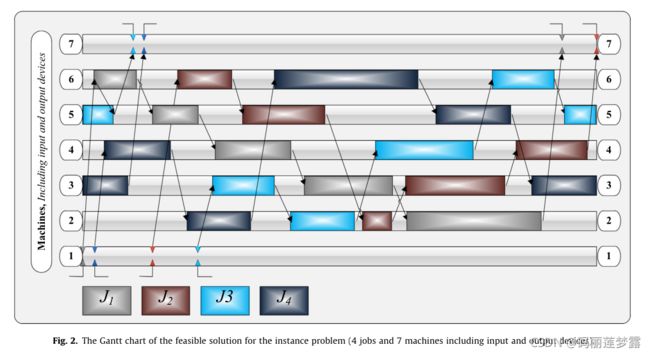
由于CJS-RCS问题的特殊情况，在周期开始时，可能会有一些机器被相关工件的工序占用。图2表示占用的两台机器(机器3和5)和占用的工件(分别位于这两台机器上的工件4和3)，以获得实例问题的可行解决方案。当工件加工完成时，不同颜色的箭头标识用于工件运输的机器人。图中所示实例问题可行解的运输工件开始时间。此外，图3还说明了实例问题的连续循环甘特图。让我们考虑一下工作的高度hj。它表示为作业的特定实例从头到尾在系统中停留的周期数。

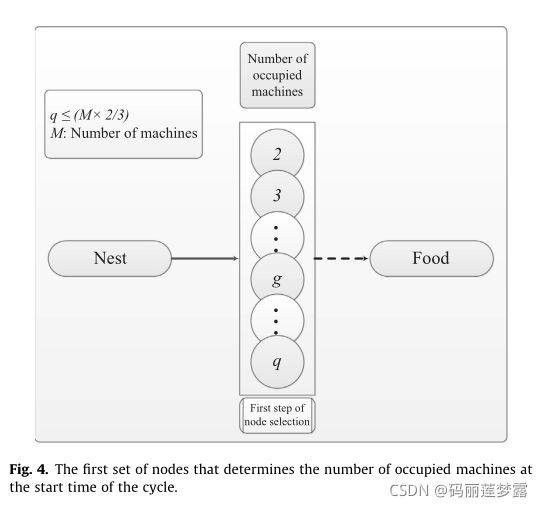
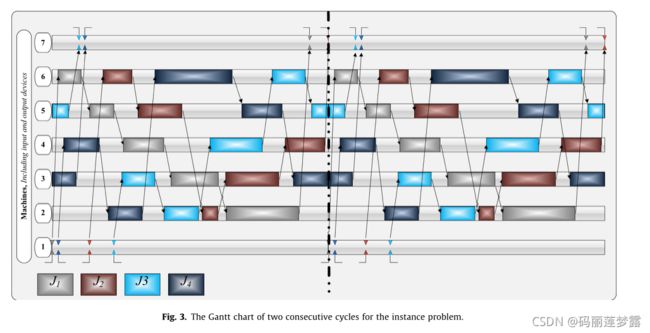  在求解CJS-RCS问题时，应考虑每个作业的运输作业之间的优先约束。为了识别这些优先约束，求解过程必须确定周期开始时占用的机器数，这是CJS-RCS问题的第一个子问题。对于该子问题，提出的MB-ACO的第一个节点集的图表示如图4所示。

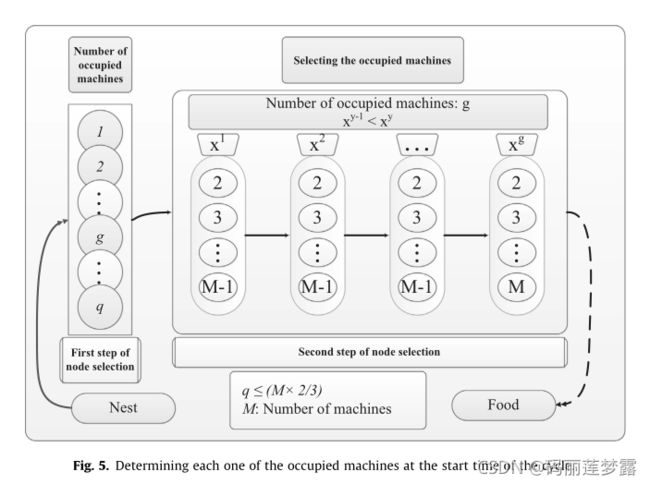
 作为第二个子问题，考虑蚂蚁通过的第二个节点集来确定每一台被占用的机器。MBACO的第二节点集的图形表示如图5所示.

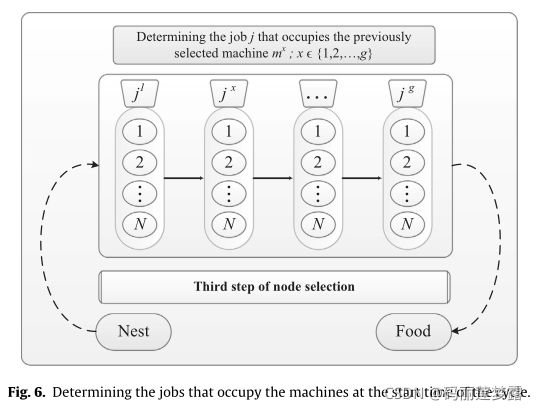
 让我们以递增的顺序来考虑周期开始时的占用机器集(SOM)。第三个子问题是确定占用每台选定机器(Mx2SOM)的工件，表示该子问题的第三组节点如图6所示。

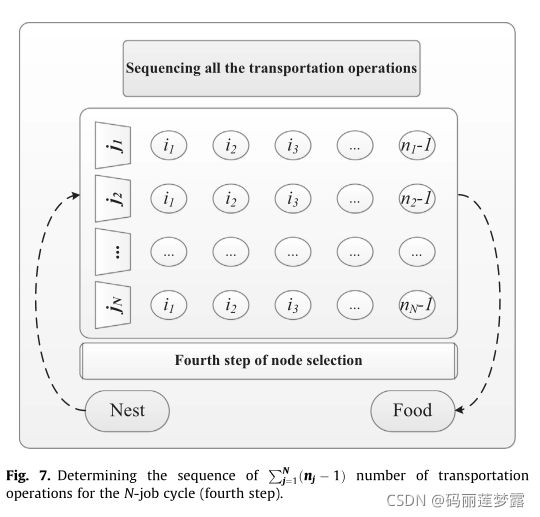
 3.2 运输作业的排序

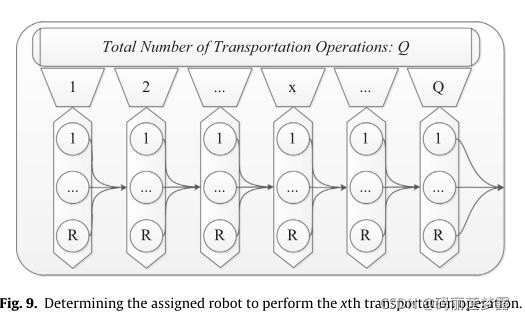
3.3 指派机器人给运输任务

 3.4 MB-ACO的总体框架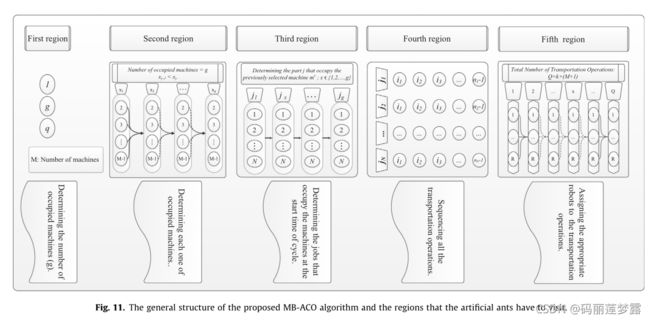

4 这篇文章蚁群算法的框架代码实现

4.1 信息素初始化

        这篇文章对于所有的边，信息素跟踪值都被初始化为1(1.0)。

4.2 转移规则

蚂蚁选择下一节点b根据下式确定，其中q0为给定概率值，q为随机生成的概率值：

        

B_select的产生根据下列规则，首先对所有可选边的信息素进行标准化：

 

然后构造PD如下：

其中PR中的元素以U[0,1]随机生成，然后选取PD中对应值最大的节点作为B_select,具体证明可见原文。

4.3 信息素更新

4.3.1 局部更新

 

4.3.2 全局更新

 

 4.4 框架代码

4.4.1 算例

'''
start date:2021/10/26 11:20
[1]Elmi,,Atabak,Topaloglu,,& Seyda.(2017).Cyclic job shop robotic cell scheduling problem: 
Ant colony optimization.COMPUTERS AND INDUSTRIAL ENGINEERING,111,417-432.
'''
import random
import numpy as np
import copy

def generator(J_num,M_num,R_num):
    '''
    There are three groups of problems with respect to the number of jobs in the robotic cell,
    which are 10,15,and 20,respectively.the maximum height of the cycles are considered to be 5 for all three group of problem,
    separately.
    -The standard processing times of the machines are generated from the uniform distribution U[100,200].
    
    -The time needed for the loaded robot moves between the successive machines,
     which are considered as transportation operations, are generated using the uniform distribution U[25,50].
     
    -The time needed for the unloaded robot moves between the machines, which are considered as empty moves,
     are generated from the uniform distribution U[10,25].
    
    :param J_num: the number of jobs
    :param M_num: the number of processing machines
    :param R_num: the number of singer gripper robots
    :return: 
    '''
    PT=[]
    PM=[]
    lis=[_ for _ in range(M_num)]
    for i in range(J_num):
        PT.append([random.randint(100,200) for _ in range(M_num)])
        random.shuffle(lis)

        PM.append(copy.copy(lis))
    LT=np.identity(M_num)
    for i in range(M_num):
        for j in range(M_num):
            if LT[i,j]==0 and i!=j:
                LT[i,j]=random.randint(25,50)
                LT[j,i]=LT[i,j]
            elif LT[i,j]==1:
                LT[i,j]=0
    ULT = np.identity(M_num)
    for i in range(M_num):
        for j in range(M_num):
            if ULT[i, j] == 0 and i != j:
                ULT[i,j] = random.randint(10,25)
                ULT[j,i] = ULT[i,j]
            elif ULT[i, j] == 1:
                ULT[i, j] = 0

    return PT,PM,LT,ULT

PT,PM,LT,ULT=generator(10,5,3)

4.4.2 蚁群框架 

class Ant:
    def __init__(self):
        self.g=None
        self.occupied_Machines=[]
        self.occupied_Jobs=[]
        self.Transport_sequence=[]
        self.assigned_robot=[]

import numpy as np
import random

class Ant_Map:
    def __init__(self,args):
        self.args=args
        self.First_Region=np.ones(int(args.m*2/3))  #Determining the number of occupied Machines(g)
        self.Second_Region=[]                       #Determining each one of occupied machines
        for i in range(len(self.First_Region)):
            self.Second_Region.append(np.ones((i+1,args.m)))
        self.Third_Region=[]                        #Determining the jobs that occupy the machines at the start time of cycle.
        for i in range(len(self.First_Region)):
            self.Third_Region.append(np.ones((i+1, args.n)))
        self.Fourth_region=np.ones((args.n,args.m)) #Sequencing all the transportion operations
        Q=args.n*args.m
        self.Fifth_Region=np.ones((Q,args.r))  #Assigning the appropriate robots to the transpotation operations
        self.p=args.p
        self.p0=args.P0
        self.p0_episode=args.P0_episode
        self.t0=args.t0
        self.s=args.s
        self.episode=args.episode

    #add pheromone
    def Map_update(self,map,site):
        if type(site)!='list':
            map[site]+=self.p*self.t0
        else:
            map[site[0],site[1]]+=self.p*self.t0

    #evaporating pheromone
    def Map_evaporate(self):
        self.First_Region=self.First_Region*self.p
        self.Second_Region=self.Second_Region*self.p
        self.Third_Region=self.Third_Region*self.p
        self.Fourth_region=self.Fourth_region*self.p
        self.Fifth_Region=self.Fifth_Region*self.p

    def Transition(self,Pheromone_matrix):
        self.p0 += self.p0_episode  # compared with article,we add a adaptive operator
        #step 1 :normalized pheromone trail of edge
        t_total=sum(Pheromone_matrix)
        PH=[Pheromone_matrix[i]/t_total for i in range(len(Pheromone_matrix))]
        PR=[random.random() for _ in range(len(Pheromone_matrix))]
        PD=[PH[_]-PR[_]  for _ in range(len(PH)) ]
        if random.random()