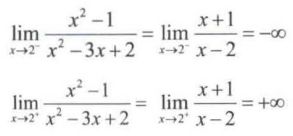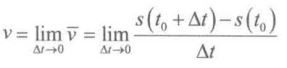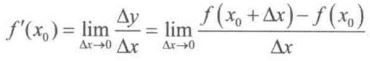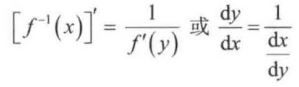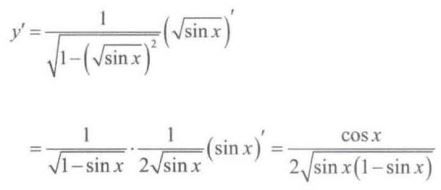人工智能之数学基础篇—高等数学基础中
人工智能之数学基础篇—高等数学基础中
- 4 连续性与导数
-
- 4.1 函数连续性定义
- 4.2 函数连续性需要满足的条件
- 4.3 函数的间断点
- 4.4 函数间断点的常见类型
- 4.5 导数
-
- 4.5.1 导数的定义
- 4.5.2 导数的几何意义
- 4.5.3 导数的基本求导法则
- 4.5.4 反函数的求导法则
- 4.5.5 复合函数的求导法则
- 4.5.6 常用的求导公式
- 5 偏导数
-
- 5.1 偏导数的定义
- 5.2 偏导数的几何意义
在这篇文章,我将简单的总结一下连续性与导数、偏导数、方向导数等高等数学基本概念,这些概念是理解人工智能算法的基础数学知识。
4 连续性与导数
函数建立了变量之间的依存关系,有时候也需要考虑函数的连续性。例如气温的变化,当时间变动微小时,气温的变化也很微小,这种特点就是所谓的连续性。
4.1 函数连续性定义
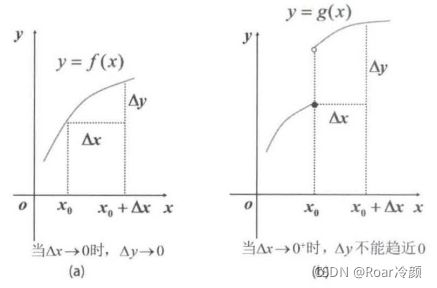
定义13 设函数 f ( x ) f(x) f(x) 在 x 0 x_{0} x0 的某个邻域内有定义,当自变量的增量 Δ x \Delta x Δx 趋于 0 时,对应的函数的增量 Δ y = f ( x 0 + Δ x ) − f ( x 0 ) \Delta y = f(x_{0}+\Delta x) - f(x_{0}) Δy=f(x0+Δx)−f(x0) 也趋于 0,即
lim Δ x → 0 Δ y = lim Δ x → 0 [ f ( x 0 + Δ x ) − f ( x 0 ) ] = 0 \lim_{\Delta x\rightarrow 0} \Delta y = \lim_{\Delta x\rightarrow 0}[f(x_{0}+\Delta x) - f(x_{0})]=0 Δx→0limΔy=Δx→0lim[f(x0+Δx)−f(x0)]=0
则称函数 f ( x ) f(x) f(x) 在点 x 0 x_{0} x0 处连续。
观察图6所示:图(a),当 Δ x → 0 \Delta x \rightarrow 0 Δx→0时, Δ y → 0 \Delta y \rightarrow 0 Δy→0,因此函数 f ( x ) f(x) f(x) 在点 x 0 x_{0} x0 处连续。再来看图(b),当 Δ x → 0 + \Delta x \rightarrow 0^{+} Δx→0+时, Δ y \Delta y Δy 的改变非常大,因此函数 g ( x ) g(x) g(x) 在点 x 0 x_{0} x0 处不连续。
4.2 函数连续性需要满足的条件
函数 f ( x ) f(x) f(x) 在点 x 0 x_{0} x0 处连续,需要满足以下条件:
(1)函数在该点处有定义。
(2)函数在该点处极限 lim x → x 0 f ( x ) \lim_{x\rightarrow x_{0}} f(x) limx→x0f(x) 存在。
(3)极限值等于函数值 f ( x 0 ) f(x_{0}) f(x0) 。
三个条件缺一不可。
【例9】已知函数 f ( x ) = { x + 1 , x ⩽ 0 s i n x x , x > 0 f(x)=\left\{\begin{matrix} x+1, & x\leqslant 0\\ \frac{sinx}{x}, & x>0 \end{matrix}\right. f(x)={ x+1,xsinx,x⩽0x>0,判断函数 f ( x ) f(x) f(x) 在点 x = 0 x = 0 x=0 处的连续性。
解:
f ( 0 ) = 1 , lim x → 0 − ( x + 1 ) = 1 , lim x → 0 + s i n x x = 1 f(0)=1, \lim_{x\rightarrow 0^{-}} (x+1)= 1, \lim_{x\rightarrow 0^{+}} \frac{sinx}{x}= 1 f(0)=1,x→0−lim(x+1)=1,x→0+limxsinx=1
极限存在并且等于 f ( 0 ) f(0) f(0),满足3个条件,因此函数 f ( x ) f(x) f(x) 在点 x = 0 x = 0 x=0 处连续。
4.3 函数的间断点
设函数 f ( x ) f(x) f(x) 在 x 0 x_{0} x0 的某个去心邻域内有定义,如果函数 f ( x ) f(x) f(x) 有下列 3 种情况之一,那么函数 f ( x ) f(x) f(x) 在点 x 0 x_{0} x0 处不连续,点 x 0 x_{0} x0 称为函数 f ( x ) f(x) f(x) 的间断点或不连续点。
(1)函数 f ( x ) f(x) f(x) 在点 x = x 0 x=x_{0} x=x0 处没有定义。
(2)函数 f ( x ) f(x) f(x) 虽然在点 x = x 0 x=x_{0} x=x0 处有定义,但是在该点处极限 lim x → x 0 f ( x ) \lim_{x\rightarrow x_{0}} f(x) limx→x0f(x) 不存在。
(3)函数 f ( x ) f(x) f(x) 虽然在点 x = x 0 x=x_{0} x=x0 处有定义,且在该点处极限 lim x → x 0 f ( x ) \lim_{x\rightarrow x_{0}} f(x) limx→x0f(x) 存在,但 lim x → x 0 f ( x ) ≠ f ( x 0 ) \lim_{x\rightarrow x_{0}} f(x) \neq f(x_{0}) limx→x0f(x)=f(x0) 。
4.4 函数间断点的常见类型
通常把间断点分为两类:如果 a a a 是函数 f ( x ) f(x) f(x) 的间断点,且函数在该点左右极限都存在 ,则称 a a a 为第一类间断点;不是第一类间断点的任何间断点,都称为第二类间断点。
第一类间断点又可以分为以下两类 。
(1)跳跃间断点: lim x → x 0 + f ( x ) \lim_{x\rightarrow x_{0}^{+}}f(x) limx→x0+f(x)、 lim x → x 0 − f ( x ) \lim_{x\rightarrow x_{0}^{-}}f(x) limx→x0−f(x) 极限都存在,但 lim x → x 0 + f ( x ) ≠ lim x → x 0 − f ( x ) \lim_{x\rightarrow x_{0}^{+}}f(x) \neq \lim_{x\rightarrow x_{0}^{-}}f(x) limx→x0+f(x)=limx→x0−f(x)。
(2)可去间断点: lim x → x 0 + f ( x ) \lim_{x\rightarrow x_{0}^{+}}f(x) limx→x0+f(x)、 lim x → x 0 − f ( x ) \lim_{x\rightarrow x_{0}^{-}}f(x) limx→x0−f(x) 极限都存在且相等,但是 lim x → x 0 f ( x ) ≠ f ( x 0 ) \lim_{x\rightarrow x_{0}} f(x) \neq f(x_{0}) limx→x0f(x)=f(x0) 或 f ( x ) f(x) f(x) 在该点无定义。
【例10】分析函数 f ( x ) = x 2 − 1 x 2 − 3 x + 1 f(x)=\frac{x^{2}-1}{x^{2}-3x+1} f(x)=x2−3x+1x2−1 的连续性
解:函数在点 x = 2 x = 2 x=2 、 x = 1 x = 1 x=1 处没有定义,因此点 x = 2 x = 2 x=2 、 x = 1 x = 1 x=1 为间断点 。
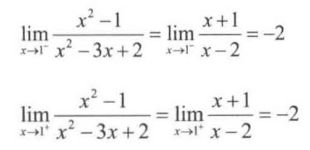
lim x → 1 − f ( x ) = lim x → 1 + f ( x ) ≠ f ( 1 ) \lim_{x\rightarrow 1^{-}}f(x)=\lim_{x\rightarrow 1^{+}}f(x) \neq f(1) limx→1−f(x)=limx→1+f(x)=f(1),因此在点 x = 1 x = 1 x=1 处是可去间断点 。
因此,在点 x = 2 x = 2 x=2 处是第二类间断点 。
4.5 导数
导数是一个非常重要的概念,对于很多实际应用问题的求解都会用到导数。 先来看一个引例:速度问题。历史上速度问题与导数概念的形成有着密切的关系。
我们都知道平均速度 v = s t v = \frac{s}{t} v=ts,那么如何表示瞬时速度呢?
瞬时经过路程: Δ s = s ( t 0 + Δ t ) − s ( t 0 ) \Delta s = s(t_{0}+\Delta t)-s(t_{0}) Δs=s(t0+Δt)−s(t0)
这一小段 Δ t \Delta t Δt 的平均速度:
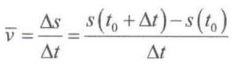
当 Δ t → 0 \Delta t \rightarrow 0 Δt→0 时,对应的 v ˉ \bar{v} vˉ 就是瞬时速度。在时刻 t 0 t_{0} t0 的瞬时速度为:
4.5.1 导数的定义
定义14 设函数 f ( x ) f(x) f(x) 在 x 0 x_{0} x0 的某个邻域内有定义,当自变量的增量为 Δ x \Delta x Δx 时,对应的函数的增量 Δ y = f ( x 0 + Δ x ) − f ( x 0 ) \Delta y = f(x_{0}+\Delta x) - f(x_{0}) Δy=f(x0+Δx)−f(x0) 。当 Δ x → 0 \Delta x \rightarrow 0 Δx→0 时, Δ y Δ x \frac{\Delta y }{\Delta x} ΔxΔy 的极限存在,则称函数 f ( x ) f(x) f(x) 在 x 0 x_{0} x0 处可导。 此极限值为函数 f ( x ) f(x) f(x) 在点 x 0 x_{0} x0 处的导数,记作 f ′ ( x ) f^{'}(x) f′(x),即
4.5.2 导数的几何意义
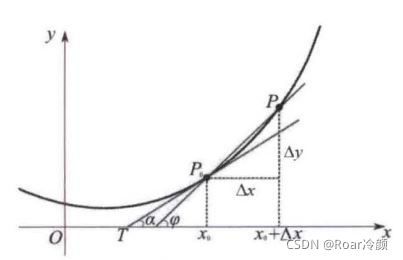
通常函数 y = f ( x ) y=f(x) y=f(x) 的导数表示了因变量 y y y 在点 x 0 x_{0} x0 处随自变量 x x x 变化的快慢程度,即函数的变化速率。 从几何意义上讲,函数在某一点 x 0 x_{0} x0 的变化率等于这一点的切线的斜率,图7中 P 0 P_{0} P0 的导数为在点 P 0 P_{0} P0 处所作切线的斜率, f ′ ( x 0 ) = t a n α f^{'}(x_{0}) = tan\alpha f′(x0)=tanα,其中 α \alpha α 是切线的倾角(与 x x x 轴正方向的夹角)。
4.5.3 导数的基本求导法则
如果函数 u = u ( x ) u=u(x) u=u(x) 、 ν = ν ( x ) ν=ν(x) ν=ν(x) 都在点 x x x 有导数,那么它们的和 、差、 积 、 商(除分母为 0 的点外)都在点 x x x 具有导数,且满足以下法则 。

4.5.4 反函数的求导法则
设函数 x = f ( y ) x=f(y) x=f(y) 在区间 D y D_{y} Dy 内单调可导,且 f ′ ( y ) ≠ 0 f^{'}(y)\neq 0 f′(y)=0,那么它的反函数 y = f − 1 ( x ) y = f^{-1}(x) y=f−1(x) 在区间 D x = { x = f ( y ) , y ϵ D y } D_{x}=\left \{ x=f(y),y\epsilon D_{y} \right \} Dx={ x=f(y),yϵDy} 内也可导,且满足下式:
4.5.5 复合函数的求导法则
如果 u = g ( x ) u=g(x) u=g(x) 在点 x x x 处可导, y = f ( u ) y=f(u) y=f(u) 在点 u = g ( x ) u=g(x) u=g(x) 处可导,那么复合函数 y = f [ g ( x ) ] y=f\left [ g(x) \right ] y=f[g(x)] 在点 x x x 处可导,且其导数为:
d y d x = f ′ ( u ) ⋅ g ′ ( x ) / d y d x = d y d u ⋅ d u d x \frac{dy}{dx}=f^{'}(u)\cdot g^{'}(x)/\frac{dy}{dx}=\frac{dy}{du}\cdot \frac{du}{dx} dxdy=f′(u)⋅g′(x)/dxdy=dudy⋅dxdu
4.5.6 常用的求导公式
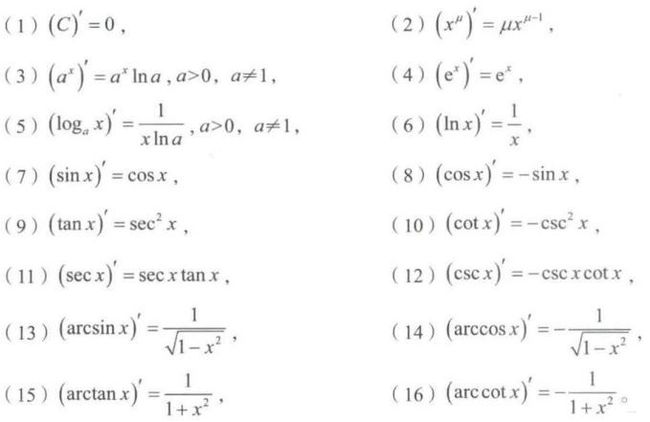
【例11】求函数 y = a r c s i n s i n x y=arcsin\sqrt{sinx} y=arcsinsinx 的导数,并用 Python 编程求导。
from sympy import *
from sympy.abc import x,y,z,f
result= diff(asin(sqrt(sin(x))))
print(result)
cos(x)/(2*sqrt(1 - sin(x))*sqrt(sin(x)))
5 偏导数
如果涉及的函数都只有一个自变量,那么这种函数被称为一元函数,但在很多研究领域中,经常需要研究多个变量之间的关系,在数学上,这就表现为一个变量与另外多个变量的相互依赖关系。由此就引出来了偏导数的概念。
先来研究二元函数。二元函数是函数值 z z z 随着两个自变量的变化而变化,记为 z = f ( x , y ) z =f(x,y) z=f(x,y) ,其图形是一个 x , y x,y x,y 轴展开的曲面,如图 8 所示。
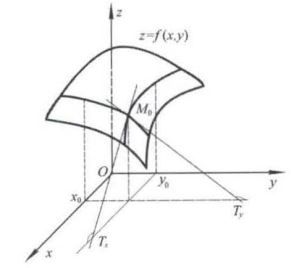
一元函数的导数反映了函数相对于自变量的变化率。 但多元函数的自变量有两个或两个以上,函数对于自变量的变化率问题更为复杂,但有规律可循。一般来说,对于多元函数 ,在研究某一个自变量的变化率时,往往把其余的自变量暂时固定下来,即视为常数,使其成为一元函数,然后再对其进行求导,这就是偏导数的概念 。
5.1 偏导数的定义
定义15 设函数 z = f ( x , y ) z = f(x,y) z=f(x,y) 在点 ( x 0 , y 0 ) (x_{0}, y_{0}) (x0,y0) 的某个邻域内有定义,当 y y y 固定在 y 0 y_{0} y0,而 x x x 在 x 0 x_{0} x0 处有增量 Δ x \Delta x Δx,函数有增量 f ( x 0 + Δ x , y 0 ) − f ( x 0 , y 0 ) f\left ( x_{0}+\Delta x,y_{0} \right )-f\left ( x_{0}, y_{0}\right ) f(x0+Δx,y0)−f(x0,y0),如果极限
lim Δ x → 0 f ( x 0 + Δ x , y 0 ) − f ( x 0 , y 0 ) Δ x \lim_{\Delta x\rightarrow 0}\frac{f\left ( x_{0}+\Delta x,y_{0} \right )-f\left ( x_{0}, y_{0}\right )}{\Delta x} Δx→0limΔxf(x0+Δx,y0)−f(x0,y0)
存在,则称此极限为函数 z = f ( x , y ) z = f(x,y) z=f(x,y) 在点 ( x 0 , y 0 ) (x_{0}, y_{0}) (x0,y0) 处对 x x x 的偏导数,记为 f x ( x 0 , y 0 ) f_{x}\left ( x_{0}, y_{0}\right ) fx(x0,y0),即
f x ( x 0 , y 0 ) = lim Δ x → 0 f ( x 0 + Δ x , y 0 ) − f ( x 0 , y 0 ) Δ x f_{x}\left ( x_{0}, y_{0}\right ) = \lim_{\Delta x\rightarrow 0}\frac{f\left ( x_{0}+\Delta x,y_{0} \right )-f\left ( x_{0}, y_{0}\right )}{\Delta x} fx(x0,y0)=Δx→0limΔxf(x0+Δx,y0)−f(x0,y0)
同理可得:
f y ( x 0 , y 0 ) = lim Δ y → 0 f ( x 0 , y 0 + Δ y ) − f ( x 0 , y 0 ) Δ y f_{y}\left ( x_{0}, y_{0}\right ) = \lim_{\Delta y\rightarrow 0}\frac{f\left ( x_{0},y_{0} +\Delta y \right )-f\left ( x_{0}, y_{0}\right )}{\Delta y} fy(x0,y0)=Δy→0limΔyf(x0,y0+Δy)−f(x0,y0)
5.2 偏导数的几何意义
偏导数的几何意义可直接由一元函数导数的几何意义得出,由于 f x ( x 0 , y 0 ) f_{x}\left ( x_{0}, y_{0}\right ) fx(x0,y0) 就是 z = f ( x , y 0 ) z = f(x,y_{0}) z=f(x,y0) 在 x = x 0 x=x_{0} x=x0 处的导数,而 z = f ( x , y 0 ) z = f(x,y_{0}) z=f(x,y0) 在几何上可以看作是平面 y = y 0 y=y_{0} y=y0 截曲面 z = f ( x , y ) z = f(x,y) z=f(x,y) 得到的曲线 C x C_{x} Cx。因此 f x ( x 0 , y 0 ) f_{x}\left ( x_{0}, y_{0}\right ) fx(x0,y0) 的几何意义为:曲线 C x C_{x} Cx 在点 M 0 ( x 0 , y 0 , z 0 ) M_{0}\left ( x_{0},y_{0},z_{0} \right ) M0(x0,y0,z0) 处切线 M 0 T x M_{0}T_{x} M0Tx 对 x x x 轴的斜率,如图9所示。
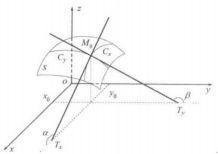
同理,若 C y C_{y} Cy 是平面 x = x 0 x=x_{0} x=x0 截曲面 z = f ( x , y ) z = f(x,y) z=f(x,y) 得到的曲线,则偏导数 f y ( x 0 , y 0 ) f_{y}\left ( x_{0}, y_{0}\right ) fy(x0,y0) 的几何意义为:曲线 C y C_{y} Cy 在点 M 0 ( x 0 , y 0 , z 0 ) M_{0}\left ( x_{0},y_{0},z_{0} \right ) M0(x0,y0,z0) 处切线 M 0 T y M_{0}T_{y} M0Ty 对 y y y 轴的斜率,如图9所示。
【例12】求 f ( x , y ) = x 2 + 3 x y + y 2 f\left ( x,y \right )=x^{2}+3xy+y^{2} f(x,y)=x2+3xy+y2 在点 ( 1 , 2 ) (1,2) (1,2) 处的偏导数,并用 Python 编程求导。
解:
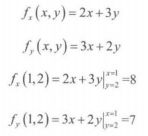
【代码如下】
>>> from sympy import *
>>> from sympy.abc import x,y,z,f
>>> f = x**2 + 3*x*y + y**2
>>> diff(f,x) #对x求偏导
2*x + 3*y
>>> diff(f,y) #对y求偏导
3*x + 2*y
>>> fx = diff(f,x) #对x求偏导并将结果赋给fx
>>> fx.evalf(subs={
x:1,y:2}) #以字典的形式传入多个变量的值,求函数值
8.00000000000000
>>> fy = diff(f,y)
>>> fy.evalf(subs={
x:1,y:2})
7.00000000000000