【随学随想】线性判别分析（Linear Discriminant Analysis）判别鸢尾花种类

理论介绍

LDA思想

线性判别分析（LDA）是一种经典的二分类模型，其主要应用于二分类问题以及降维，由于他最早由R.A.Fisher提出（也就是大名鼎鼎的Iris数据集的收集者），所以又称为Fisher判别
LDA的思想非常简单，就是将训练集往某一方向的平面（1维者线，2维者面也）投影（降维），并且使同类的样本点尽可能的近，异类的样本点尽可能的远（有点聚类的意思，也可以类比成高内聚，低耦合），当对新样本进行训练时，将其投影至平面上，再根据投影后新样本的距离来判断其属于哪一类

最优的投影平面

假设有数据集为$D=\{(x_i,y_i)\},y_i\in \{0,1\}$,令$X_i,{\mu }_i,{\sum }_i$为第$i\in \{0,1\}$类样本的集合，均值向量以及协方差，我们将样本点投影到直线$\omega$上,即$$y={\omega }^{T}x$$，则两类点中心在直线上的投影分别为${\omega }^T{\mu }_0,{\omega }^T{\mu }_1$，若将所有点投影至线上，则其协方差分别为${\omega }^T{\sum }_0\omega ,{\omega }^T{\sum }_1{\omega }^T$,在本例中，我们将维度降为一维，故上述四者皆为实数。

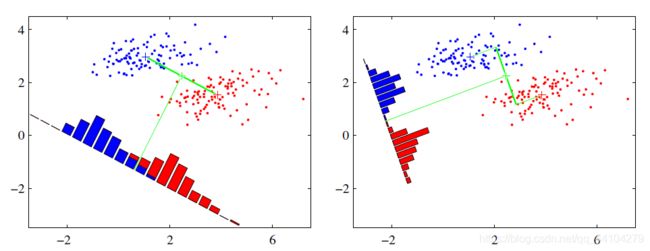
若使得优化目标:类间样本尽量近，类与类的中心尽量的远，则需要使得${\omega }^T{\sum }_0\omega +{\omega }^T{\sum }_1{\omega }^T$尽可能地小,且需要$||{\omega }^T{\mu }_0-{\omega }^T{\mu }_1|{|}^2$尽量地大，故此时我们所需要考虑的优化目标为:$$J=\frac{||{\omega }^T{\mu }_0-{\omega }^T{\mu }_1|{|}^2}{{\omega }^T{\sum }_0\omega +{\omega }^T{\sum }_1{\omega }^T}$$
我们再定义“类内散度矩阵”:$$S_{\omega }=\sum _0+\sum _1$$
以及类间散度矩阵:$$S_b=({\mu }_0-{\mu }_1)({\mu }_0-{\mu }_1{)}^T$$
由此，我们将上面的方程改写为:$$J=\frac{{\omega }^T{S}_b\omega }{{\omega }^T{S}_{\omega }\omega }$$
上式又称$S_{\omega }$与$S_b$的广义瑞利商
如何确定$\omega$？我们令${\omega }^T{S}_{\omega }\omega =1$，则可得等价条件$$mi{n}_{\omega }-{\omega }^T{S}_b\omega$$
$$st.{\omega }^T{S}_{\omega }\omega =1$$
此时，我们利用拉格朗日乘子法，得:$$S_b\omega =\lambda S_{\omega }\omega$$
其中$\lambda$为拉格朗日乘子,则有:$$S_b\omega =\lambda ({\mu }_0-{\mu }_1)$$
最后综合各式得:$$\omega =S_{\omega }^{-1}({\mu }_0-{\mu }_1)$$

其中，$S_{\omega }^{-1}$由对$S_{\omega }$进行奇异值分解得到

程序代码

关于鸢尾花数据集的相关背景，我有在我的另一篇博文《【随学随想】logistic回归判别鸢尾花种类》中有提到，在这我不再做过多介绍，我将链接放在下面，供朋友们阅读及回忆
《随学随想】logistic回归判别鸢尾花种类》
在这里，我想介绍下sci-kit learn库

sci-kit learn库

sci-kit learn库，简称sklearn库，是用于Python编程语言的免费软件机器学习库。它具有各种分类，回归和聚类算法，包括支持向量机，随机森林，梯度提升，k均值和DBSCAN，旨在与Python数值和科学库NumPy和SciPy进行互操作（本段摘自sci-kit learn的英文维基百科条目），其高度封装，使用的代码少，易上手，且精度高

mport numpy as np
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

我们在这里将调用sklearn discriminant_analysis子包中的LinearDiscriminantAnalysis方法对数据进行训练

数据导入

本文对鸢尾花数据的预处理，训练集及测试集的划分均与文章《【随学随想】logistic回归判别鸢尾花种类》一样，即

'''本程序利用LDA判別對鳶尾花的種類進行判別，其判別的
的對象跟Logistic回歸例子一樣'''

Iris = np.loadtxt('D:/TheSecondFile/iris.data', dtype='str', delimiter=',')

Data_X = Iris[:, 0:4].astype('float')
Data_Y = Iris[:, 4]

for i in range(len(Data_Y)):
    if Data_Y[i] == 'Iris-setosa':
        Data_Y[i] = 0
    if Data_Y[i] == 'Iris-versicolor':
        Data_Y[i] = 1
    if Data_Y[i] == 'Iris-virginica':
        Data_Y[i] = 2

X_train = np.zeros((93, 4))
Y_train = np.zeros((93, 1))
X_test = np.zeros((20, 4))
Y_test = np.zeros((20, 1))

'''設置訓練集，測試集'''

# 訓練集
for i in range(40):
    X_train[i] = Data_X[i]
    Y_train[i] = Data_Y[i]
for i in range(50, 90):
    X_train[i - 10] = Data_X[i]
    Y_train[i - 10] = Data_Y[i]

# 測試集
for i in range(40, 50):
    X_test[i - 40] = Data_X[i]
    Y_test[i - 40] = Data_Y[i]
for i in range(90, 100):
    X_test[i - 80] = Data_X[i]
    Y_test[i - 80] = Data_Y[i]

模型训练

clf = LinearDiscriminantAnalysis(n_components=1).fit(X_train, Y_train)

在这里，参数n_components意味着我们需要降至的维度，由于我们需要将其训练成直线，故我们将n_components设为1.
然后，我们调用模型的fit方法对模型进行训练，fit()内第一项为自变量，第二项为因变量

预测测试集

outcome = clf.predict(X_test).astype('int')

我们使用训练好的模型的predict方法对测试集进行预测，并令输出结果为整数

输出结果与计算正确率

print("預測結果")
print(outcome)
print("實際結果")
print(np.ravel(Y_test.T.astype('int')))

# 判斷正確率
j0 = 0
for i in range(len(outcome)):
    if outcome[i] == Y_test[i]:
        j0 = j0 + 1

correct_rate_percentage = (j0 / len(outcome)) * 100
print("預測的正確率為{:.2f}%".format(correct_rate_percentage))

输出结果与正确率为:

預測結果
[0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1]
實際結果
[0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1]
預測的正確率為100.00%