2021.01.21刷题总结

问题C:奶牛们的杂技

描述
在我农场上有N头牛（1<=N<=50000），我想出了一个杂技特技：站到彼此上面，形成一个有一定高度的垂直堆叠，我就让这些牛来练习这个杂技,牛正在试图弄清楚它们应该在这堆奶牛中排列的顺序。每头N头牛具有相关的体重(1<=W_i<=10000)和强度(1<=S_i<=1000000000)。一头牛倒下的风险等于它身上所有牛的总体重（当然不包括它自己的体重）减去它的强度（这样一来，一头更强壮的牛的风险就更低）。你的任务是确定牛的顺序，使任何一头牛的最大风险最小化。

格式
输入格式
第1行：整数N为单行。

行2…N+1：行i+1用两个空分整数W和S描述牛。

输出格式

一个单一的整数，给出所有奶牛的最大风险，在任何优化排序，使风险最小化。

样例
样例输入 Copy
3
10 3
2 5
3 3
样例输出 Copy
2

这题放在二分题组里面，但是实际上可以用贪心做。
在说正确思路之前，我先说说错误的。我刚开始想当然以为，按照体重排降序，如果体重一样，就按照耐力排个降序就行了。最后被WA掉了…
正解：
假设有两头牛a和b（a和b相不相邻都可以），关系如图所示：

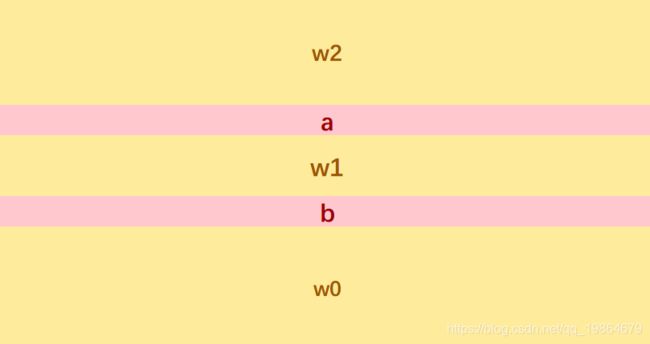
b受到的压力A1是：w2+w1+a.w-b.s
a受到的压力A2是：w2-a.s
若是把a和b的位置交换，如下图：

此时，
b受到的压力A3是：w2-b.s
a受到的压力A4是：w2+w1+b.w-a.s
因为 A4 > A2, A1 > A3,我们要使得最大的压力最小，所以 A2 和 A3 我们不需要考虑他们。
此时我们只需要判断 A4 和 A1 的大小就行了。
如果A4 A4 w2+w1+bw-a.s < w2+w1+a.w-b.s
化简得：bw+b.s < a.w+a.s
这就是最终我们需要得到的关系式，可以看出，它和w2和w1没有关系，所以不管a、b是否相邻，是否在最上面或者最下面，这个式子都通用，换句话说，这个式子适用所有情况。
至此，问题已经很清晰了，我们只需要按照这个 关系式 排个序就行了。
可是…，我还是错了很多次。
刚开始我用了vector，后来改了，发现没必要。
然后就是，没有考虑到top上面那头牛的压力，有可能它的压力是最大的嘞，谁说最上面的人压力一定就会比下面的人小嘞，嘻嘻，对叭（王者的压力不是尔等能懂的）。所以，我直接就把ans的初值写成了这样：

 ll w = 0, ans = ~(signed)INF;
    for (int i = n - 2; i >= 0; i--)
    {
     
        w += Cows[i + 1].w;
        if (ans < w - Cows[i].s)
            ans = w - Cows[i].s;
    }
    cout << ans;

这样的话，就没有考虑到最上面那头牛的压力，于是我改成了这样：

 ll w = 0, ans = w - Cows[n - 1].s;
    for (int i = n - 2; i >= 0; i--)
    {
     
        w += Cows[i + 1].w;
        if (ans < w - Cows[i].s)
            ans = w - Cows[i].s;
    }
    cout << ans;

perfect！！！
下面是AC代码：

#include 
using namespace std;
typedef unsigned long long ull;
typedef long long ll;
#define INF ((unsigned(-1)) >> 1)
const int maxn = 100100;
struct cows
{
     
    ll w, s;
};
cows Cows[maxn];
bool cmp(cows &a, cows &b)
{
     
    return a.w + a.s > b.w + b.s;
    //交换后的压力如果大于交换前的压力
}
int main(void)
{
     
    int n;
    cin >> n;
    cows temp;
    for (int i = 0; i < n; i++)
        cin >> Cows[i].w >> Cows[i].s;
    sort(Cows, Cows + n, cmp);
    ll w = 0, ans = w - Cows[n - 1].s;
    for (int i = n - 2; i >= 0; i--)
    {
     
        w += Cows[i + 1].w;
        if (ans < w - Cows[i].s)
            ans = w - Cows[i].s;
    }
    cout << ans;
}

问题 F: 插入

描述
给定一个数组A和一个目标值N，如果在数组中找到目标值则返回查找次数，如果没有则输出"NO."。

格式
输入格式
第一行数组大小

第二行数组A

第三行整数N

输出格式
输出查找的次数

样例
样例输入 Copy
4
1 3 5 6
5 样例输出 Copy
2

本来是很简单的一个题，但是这题有多组输入，然后卡了我半天。
没加多组输入之前我是错误67%，
加了多组输入之后变成了时间超限33%，我怀疑应该是我用cin导致超时了，所以我把cin换成了scanf，AC！
AC代码：

#include 
#define INF ((unsigned(-1)) >> 1)
using namespace std;
const int maxn = 1001000;
int A[maxn];
int main(void)
{
     
    int n;
    while (cin >> n)
    {
     
        for (int i = 0; i < n; i++)
            scanf("%d", &A[i]);
        sort(A, A + n);
        int x;
        cin >> x;
        int l = 0, r = n - 1, mid = l + r >> 1, count = 0;
        while (l <= r)
        {
     
            count++;
            if (A[mid] < x)
                l = mid + 1;
            else if (A[mid] > x)
                r = mid - 1;
            else
                break;
            mid = l + r >> 1;
        }
        if (A[mid] == x)
            cout << count << endl;
        else
            cout << "NO." << endl;
    }
    return 0;
}

问题 G: 生日派对分饼

描述
在我的生日派对上有N个饼，每个饼的大小不同，有许多朋友来参加我的生日派对，他们每一个人都得到了一块饼，如果其中有一个的饼比另一个人的大，他们就会抱怨，所以所有的饼应该分成相同的大小，当然了，我自己也要一块饼，而且那块也应该是同样的大小，我们所有人可能得到的最大尺寸的饼是多少？我做的饼都是圆柱形的，高度都是1，但是半径可以不一样。

格式
输入格式
一行为正整数：
测试用例的组数

然后对于每个测试用例：
一行带有两个整数N，F带有1<=N，F<=10000表示饼的数目和好友的数目。

一行N个整数ri，1<=ri<=10000：饼的半径。

输出格式
对于每个测试用例，输出一行具有最大可能的数值，这样我和我的朋友都可以得到一块大小为V的饼。答案应该以浮点数给出，绝对误差最多为10^(-7)保留6位小数。

样例
样例输入 Copy

3

3 3

4 3 3

1 24

5

10 5

1 4 2 3 4 5 6 5 4 2

样例输出 Copy

25.132741

3.141593

50.265482

提示

注意精度问题

这题和之前那个割绳子一样的，不一样的在于，这东西居然卡我精度，卡到我要吐了…
WA了十多次，唉。最后问了我全世界最好的师傅~~，师傅果然厉害！一下子就把我的问题解决了。
因为是用浮点数二分，题目要求精度是1e-7，所以我的二分是这样写的：

           double l = 0, r = max, mid = (l + r) / 2;
            double ans = 0;
            while (r - l > 1e-7)
            {
     
                //cout << ans << endl;
                if (check(mid))
                {
     
                    ans = mid;
                    l = mid;
                }
                else
                    r = mid;
                mid = (l + r) / 2.0;
            }
            printf("%.6lf\n", ans);
        }
 

然后我就疯狂被卡精度，可是我并不不知道问题在哪。
然后

最后，我改成这样：

            double l = 0, r = max, mid = (l + r) / 2;
            double ans = 0;
            for(int i=0;i<200;i++)
            {
     
                //cout << ans << endl;
                if (check(mid))
                {
     
                    ans = mid;
                    l = mid;
                }
                else
                    r = mid;
                mid = (l + r) / 2.0;
            }
            printf("%.6lf\n", ans);
        }

不管他到没到达精度，我就迭代那么多次，迭代两百次，是个鬼都能给你找出来！
AC代码：

#include 
#define INF ((unsigned(-1)) >> 1)
using namespace std;
#define PI acos(-1.0)
double cake[10100];
int n, f;
bool check(double mid)
{
     
    int count = 0;
    for (int i = 0; i < n; i++)
    {
     
        count += (int)(cake[i] / mid);
    }
    if (count >= f)
        return true;
    return false;
}
int main(void)
{
     
    int t;
    while (cin >> t)
    {
     
        while (t--)
        {
     
            double max = 0;
            cin >> n >> f;
            f++;
            for (int i = 0; i < n; i++)
            {
     
                double r;
                cin >> r;
                cake[i] = PI * r * r;
                max = max - cake[i] >= 1e-7 ? max : cake[i];
            }
            double l = 0, r = max, mid = (l + r) / 2;
            double ans = 0;
            for(int i=0;i<200;i++)
            {
     
                //cout << ans << endl;
                if (check(mid))
                {
     
                    ans = mid;
                    l = mid;
                }
                else
                    r = mid;
                mid = (l + r) / 2.0;
            }
            printf("%.6lf\n", ans);
        }
    }
    return 0;
}

学到了学到了！！！

问题 E: 中位数

描述
给定N个数字，X1，X2，……XN，让我们计算每一对数的差值：|Xi-Xj| (1 ≤ i ＜ j ≤
N),可以获得C(N,2)个数的中位数（即N*(N-1)/2个）

格式
输入格式
在每个测试用例中，N将在第一行给出。
然后Ñ编号给予，表示X 1，X 2，…，X Ñ
( Xi ≤1,000,000,000 , 3 ≤ N ≤ 1,00,000 )

输出格式
在单独的行中输出中值

样例
样例输入 Copy

4

1 3 2 4

3

1 10 2
样例输出 Copy
1
8

这题求差值的中位数，如果直接去算的话，数据太多。我们可以先把源数据排个序，然后二分找中位数。关键步骤在这里（假设x数组是升序）：

int c = 0;
    for (int i = 1, j = 2; i < n; i++)
    {
     
        while (j <= n && x[j] - x[i] < mid)
            j++;
        c += j - i - 1; //统计 mid 前面有多少个数
    }

mid是我们二分出来的一个数据
然后通过x[j] - x[i] < mid我们可以得到差值序列里面有多少个值是小于mid的
因为x是升序，所以x[j]会越来越大，x[j]-x[i]也会越来越大
while循环结束，说明x[j]-x[i]>=mid了，然后我们i++,x[j]-x[i] 的值就变小了
然后可能会再执行while循环，最后c计数
我们能够算出来差值序列里面有多少个数值在mid前面（即有多少个数比mid小）。
然后我们把c和中位数的位置(Count)比较一下
如果c

AC代码：

#include 
using namespace std;
typedef unsigned long long ull;
typedef long long ll;
#define INF ((unsigned(-1)) >> 1)
using namespace std;
const int maxn = 100100;
ll x[maxn];
ll n, size, Count;
bool check(ll mid)
{
     
    int c = 0;
    for (int i = 1, j = 2; i < n; i++)
    {
     
        while (j <= n && x[j] - x[i] < mid)
            j++;
        c += j - i - 1; //统计 mid 前面有多少个数
    }
    //cout << "mid: " << mid << " c: " << c << endl;
    if (c < Count)
        return true;
    return false;
}
int main(void)
{
     
    while (cin >> n)
    {
     
        for (ll i = 1; i <= n; i++)
            scanf("%lld", x + i);
        sort(x + 1, x + n + 1);
        //
        size = n * (n - 1) / 2;
        Count = (size + 1) / 2;
        //
        ll l = 0, r = x[n] - x[1], mid = l + r >> 1;
        ll ans = 0;
        while (l <= r)
        {
     
            if (check(mid))
            {
     
                ans = mid;
                l = mid + 1;
            }
            else
                r = mid - 1;
            mid = l + r >> 1;
        }
        cout << ans << endl;
    }
    return 0;
}

值得注意的是check函数里面的这一行：

while (j <= n && x[j] - x[i] < mid)

不能写成

while (j <= n && x[j] - x[i] <= mid)

如果差值序列是这个：1，1，1，1，2，3
这个序列中位数是1，位置是3，check函数 在检查 mid=1 时
c等于4，这样就出错了。