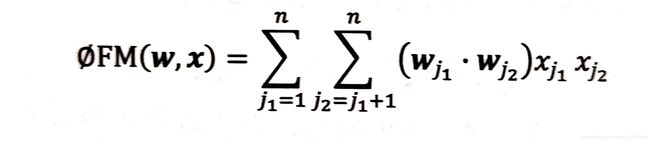【学习笔记】学习特征交叉类经典模型POLY2、FM、FFM
特征交叉类经典推荐模型——POLY2、FM、FFM
通过《深度学习与推荐系统》继续学习一下什么是特征交叉类推荐模型。这同样是一系列非常经典的推荐系统模型。上一节我们也说到了，逻辑回归LR模型很简单，同时它的表达能力不是很强，会不可避免的造成信息丢失。有很大的局限性，最主要的就是他无法同时考虑多维特征共同作用的影响，也就是特征交叉的重要作用。因为我们知道的，有些情况下仅仅依靠单一的特征而非交叉特征进行判断的情况下有时不仅会导致信息损失，甚至可能导致得出的结论是错误的。如果大家曾经了解过‘辛普森悖论’，那么也许可以更好地理解我刚才提及的情况，并认识到去利用特征交叉的重要性，我在这里简单解释一下辛普森悖论。（如果有同学学习过辛普森悖论可以跳过下面这一部分直接看正文）
*什么是辛普森悖论？
在对样本进行分组研究的时候，在分组比较重都占优势的一方，但却在总评的过程中变成了失势的一方，这种情况违背一般常理，但却现实存在，举个例子，一所美国高校的两个学院分别招生，我们想要去关注一下男女录取比例到底谁更大一些。商学院人数如下：
chart_1：商学院录取情况
而信息学院人数如下：
chart_2：信息学院录取情况
我们会发现无论如何都是女生在两个学院被优先录取。即女生的录取率比较高。那么有意思的事来了，我们将两个学院的数据合并起来一起分析：
chart_3：汇总两个学院后的录取情况
我们发现坏事了，在总评中反而是男生的录取率显得更高了。这就是著名的辛普森悖论例子。他告诉了我们什么呢，在分组实验中我们相当于是用了‘学院’+‘性别’的组合特征计算录取率，而汇总实验则使用性别这一单一的特征进行计算录取率。汇总实验对原本分组实验的两维特征惊醒了合并，损失了大量有效信息，因此无法得到正确的结果。
刚刚学习过了辛普森悖论，我们就可以回来看为什么要引入特征交叉的概念了，当我们企图利用用户数据去实施推荐的时候，如果使用LR逻辑回归模型，只对单一特征进行加权，不具备进行特征交叉生成高维组合特征的能力，因此表达能力很弱，甚至可能会得出辛普森悖论这样的错误结论。所以我们需要改造逻辑回归模型，让其具备特征交叉能力是必要的、迫切的。
特征交叉I：POLY2模型
POLY2模型其实是一种比较暴力的特征交叉方法。我们可以首先看一下它的数学形式：
For_1:POLY2模型数学表达式
非常明显，由表达式可以看出该模型对于所有的特征都进行了两两交叉(特征xj1和xj2)，并对所有的特征组合赋予了权重wh(j1,j2)。POLY2通过全面组合特征的方式，在一定程度上解决了特征组合的问题。POLY2模型本质上仍是线性模型，其训练方法与逻辑回归LR并无区别，因此便于工程商的兼容。
但是，和明显POLY2同样也存在着重大的缺陷。由于其采用了极其暴力的方式将所有特征进行了两两的交叉，这就造成了极大的数据稀疏性问题。另外，通常我们在处理数据特征时候，为了将类别特征转化为向量的时候，会使用one-hot编码方式。我们都知道one-hot编码本身就非常的稀疏，而POLY2进行无选择的特征交叉就会导致原本就很稀疏的数据更加稀疏，导致大部分的交叉特征权重缺乏有效的数据进行训练，无法收敛！另外一方面，权重的参数个数也是指数级的增加，由n变成了n²，极大地增加了训练成本。
所以说POLY2是一种暴力的特征交叉方式，但却不适合拿来处理一些我们现在面对的实际问题。算法工程师们也意识到了这一点，于是在POLY2的思路上有提出了新的方法：FM和FFM。
特征交叉II：FM因子分解机
最早提出FM的人是Rendle，他针对POLY2存在的问题在2010年正式提出了FM因子分解机模型。同样我们还是先来看一下它的数学表达式：
For_2：FM模型的数学表达式
可以看出，与POLY2相比最大的区别就在于它没有使用wh(j1,j2)作为权重，而是选择使用两个向量的内积取代了单一的权重系数。具体来说，相当于FM为每个特征学习了一个隐权重向量（论文中叫latent vector）。在特征交叉的过程中使用这学习到的两个特征的隐向量的内积来作为特征交叉计算的权重。
这有什么意义呢？意义大了去了。本质上，因子分解机（FM）这个方法跟矩阵分解（MF）用隐向量代表User-Item的做法异曲同工。可以说，FM是将矩阵分解的隐向量思想进一步扩展了，从单纯的User、Item隐向量扩展到了所有特征上。这样做的好处是非常明显的，FM通过引入了特征隐向量这个思路，直接把POLY2当时的n²级别的权重个数减少到了n*k个（这里k为FM中设置的隐向量的维度，显然n＞＞k）。在使用梯度下降法进行FM的训练过程中，FM的训练复杂度同样可以被降低到n*k级别，这极大地降低了刚才我们在讨论POLY2时提及的训练成本。
但是我们刚刚关注POLY2最严重的问题其实是严重的数据稀疏性问题。刚才我们在分析POLY2模型的时候发现由于暴力的直接对所有特征进行交叉导致数据非常稀疏，难以被学习甚至无法收敛。所以,FM为了解决这个问题，降低了学习到每个特征权重的门槛，使特征权重更容易被学习。这样说过于抽象，举个例子：在某推荐场景下，样本有两个特征分别是A和B，某训练样本的组合是（A1,B1）。如果是使用POLY2模型进行训练，那么只有当（A1,B1）组合确实地出现时才能够学习到这个组合对应的权重。但是，FM不一样，FM中A1的相关隐向量更新可以通过（A1,B2）的组合来进行，B1的隐向量也可以通过（A3,B1）来更新，着大幅度的降低了模型对于数据稀疏性的要求。而且，同时也解决了如果出现（A3，B2）这一对从未出现过的特征组合时，通过刚才的学习，模型已经学习过了A3和B2的隐向量，具备了计算该组合特征权重的能力，这是POLY2无法实现的。
所以可以看出，相比POLY2，FM虽然不具备某些具体特征组合的精确记忆能力，但是它的泛化能力却大大提高了。这种泛化能力的提高，在处理小样本数据和较为稀疏的数据时是非常有价值的。同时FM同样可以使用梯度下降法进行学习，使其不是实时性和灵活性。在2012-2014年前后FM模型非常流行。
特征交叉III：FFM模型
2015年时候，在FM的基础上，Juan提出了FFM在多项CTR大赛中东莞，并且被美团等公司应用在推荐系统和CTR领域。相比传统FM，FFM引入了特征域感知这个新的概念，其实也不复杂，就是将特征所对应的隐向量的个数进行了提高，由原来的一对一，变成了一对多，这使得FM模型具备了更强的特征表达能力。据此，我们可以得到新的数学表达式：
For_3：FFM的数学表达式
可以看出，这个表达式同刚才FM的表达式变化在于wj1变成了wj1,f2，这意味着每个特征不再是对应唯一一个因变量，而变成了一组隐变量。当xj1特征与xj2特征进行较差时，xj1特征会从它自己的一组隐向量中挑出与特征xj2的域f2相对应的隐向量wj1,f2进行交叉计算。同理xj2也会用与xj1的域f1相对应的wj2,f1隐向量来进行交叉计算。
特征域的概念解释
域（field）代表的就是特征域，域内特征一般是采用one-hot进行编码的形成的一段特征向量。比如性别这个特征分为：男、女、未知这三类，那么对于一个女性用户而言，对应的特征向量自然是[0, 1, 0]，这个三维的特征向量就是一个‘性别’的特征域。在FFM中将所有这些特征域连接起来就组成了样本的整体特征向量。（简而言之就是，一类特征就是一个特征域，每个特征域会包含多种可能的特征值）FFM关注的就是特征在其对应的特征与尚的交叉效果。
FFM中的特征交叉
我们举例来学习，现在假设我们有三种特征（即3个特征域）设为A,B,C，其中A1,B1，C1分别是这三个特征域的特征值。接下来我们对比一下FM与FFM的区别：
如果使用FM，那么A1,B1和C1都有对应的隐向量wA1,wB1,wC1，那么A1和B1特征、A1和C1做特征交叉的权重应该为wA1·wB1与wA1·wC1，其中，A1对应的隐向量wA1在两次特征交叉的过程中是相同的。
而在FFM的过程中就不同了A1与B1、A1与C1交叉运算时的特殊权重分别为wA1,B·wB1,A和wA1,C·wC1,A。可以看到在面对B1和C1时，A1使用了不同的特征与对应的隐向量与之计算内积来实现对应特征域上的特征交叉。
在FFM的训练过程中，需要学习n个特征在f个域上的k维隐向量，所以相比于FM来说的话复杂度是要高不少的，参数个数维n*k*f个（其中k为隐向量的维度）。在训练方面，FFM的二次项并不能像FM那样建华，因此其复杂度为k*n²。
所以评价FFM是需要有前提的，相比于FM而言，FFM引入了特征域的概念，为模型引入了更多有价值的信息，促使模型的到了更强的表答能力。但与此同时，FFM的计算复杂度高出了数量级的差距，在实际应用时应该在模型表达效果和成本之间进行权衡。
总结
我们再来看看当时我们在第一篇文章给大家的图：
Pic_1:早期经典推荐系统演化图
我们通过图就可以简单对今天本篇文章的内容进行总结，我们在上一章中学习了LR逻辑回归模型，但它存在特征信息丢失严重的弊端，为此我们开始考虑特征交叉，首先提出了暴力的特征交叉模型，但是这样带来的数据稀疏性问题过于突出，同时由于稀疏性伴随着较高的计算复杂度也让人难以接受。于是我们在MF的基础上考虑着用同样的思路来提出用隐向量表示特征权重进行交叉运算，于是前辈们想到了FM的方法，不仅完成了特征交叉的任务也很好的降低了运算的复杂度。在这之后面对更加复杂的场景和更高的需求，为了提取更多的准确的特征信息，前辈们创造出了特征域的概念，基于此的FM改进型模型也诞生了，FFM使每个特征在与不同域的特征交叉时采用不同的隐向量，能够提取更加准确地特征信息，提高模型表达效果。但是，特征域的引入，导致向量空间维度增加，计算复杂度再次升高，所以需要权衡成本与模型表达效果使用。
参考文献
- Factorization Machines. ICDM 2010: 995-1000
- Field-aware Factorization Machines for CTR Prediction. RecSys 2016: 43-50
- Field-aware Factorization Machines in a Real-world Online Advertising System. WWW (Companion Volume) 2017: 680-688
- Sequence-Aware Factorization Machines for Temporal Predictive Analytics. ICDE 2020: 1405-1416