1、图像锐化理论基础
1、锐化的概念
图像锐化的目的是使模糊的图像变得清晰起来,主要用于增强图像的灰度跳变部分,这一点与图像平滑对灰度跳变的抑制正好相反。而且从算子可以看出来,平滑是基于对图像领域的加权求和或者说积分运算的,而锐化则是通过其逆运算导数(梯度)或者说有限差分来实现的。
2、图像的一阶微分和二阶微分的性质
图像的锐化也就是增强图像的突变部分,那么我们也就对图像的恒定区域中,突变的开始点与结束点(台阶和斜坡突变)及沿着灰度斜坡处的微分的性质。微分是对函数局部变化率的一种表示,那么对于一阶微分有以下几个性质:
- 在恒定的灰度区域,图像的微分值为0.(灰度值没有发生变换,自然微分为0)
- 在灰度台阶或斜坡起点处微分值不为0.(台阶是,灰度值的突变变化较大;斜坡则是灰度值变化较缓慢;灰度值发生了变化,微分值不为0)
- 沿着斜坡的微分值不为0.
二阶微分,是一阶微分的导数,和一阶微分相对应,也有以下几点性质:
- 在恒定区域二阶微分值为0
- 在灰度台阶或斜坡的起点处微分值不为0
- 沿着斜坡的微分值为0.
从以上图像灰度的一阶和二阶微分的性质可以看出,在灰度值变化的地方,一阶微分和二阶微分的值都不为0;在灰度恒定的地方,微分值都为0.也就是说,不论是使用一阶微分还是二阶微分都可以得到图像灰度的变化值。
3、图像的一阶微分和二阶微分的计算
图像可以看着是二维离散函数,对于图像的一阶微分其计算公式如下:
\begin{array}{l}{\frac{\partial f}{\partial x}=f(x+1)-f(x)} \\ {\frac{\partial f}{\partial y}=f(y+1)-f(y)}\end{array}
对于二阶微分有:
\begin{array}{l}{\frac{\partial^{2} f}{\partial \tau^{2}}=f(x+1)+f(x-1)-2 f(x)} \\ {\frac{\partial^{2} f}{\partial y^{2}}=f(y+1)+f(y-1)-2 f(y)}\end{array}
在图像处理中的一阶微分通常使用梯度的幅值来实现,f在(x,y)处梯度的列向量为:
$\nabla f=\operatorname{grad}(f)=\left[ \begin{array}{l}{g_{x}} \\ {g_{y}}\end{array}\right]=\left[ \begin{array}{l}{\frac{\partial f}{\partial x}} \\ {\frac{\partial f}{\partial y}}\end{array}\right]$
该向量表示图像中的像素在点(x,y)处灰度变化率最大的方向。
这个列向量的幅值就是图像f(x,y)的梯度图:
$M(x, y)=\operatorname{mag}(\nabla f)=\sqrt{g_{x}^{2}+g_{y}^{2}}$
由于求平方的根运算比较费时,通常可以使用绝对值的和来近似
$$
M(x, y) \approx\left|g_{x}\right|+\left|g_{y}\right|
$$
对于二阶微分的计算,则有:
$$
\nabla^{2} f=\frac{\partial^{2} f}{\partial x^{2}}+\frac{\partial^{2} f}{\partial y^{2}}
$$
其中:
$$
\begin{aligned} \frac{\partial^{2} f}{\partial x^{2}} &=f(x+1, y)+f(x-1, y)-2 f(x, y) \\ \frac{\partial^{2} f}{\partial y^{2}} &=f(x, y+1)+f(x, y-1)-2 f(x, y) \end{aligned}
$$
2、基于一阶导的梯度算子
1、Robort算子
根据梯度的定义
$\begin{aligned} g_{x} &=f(x+1, y)-f(x, y) \\ g_{y} &=f(x, y+1)-f(x, y) \end{aligned}$
可以得到模板$\left[ \begin{array}{ll}{-1} & {1}\end{array}\right]$和$\left[ \begin{array}{c}{-1} \\ {1}\end{array}\right]$
可以看出,得到的边缘一部分是在内边界,一部分是外边界,并且,黄色像素点并未有计算结果,也就是,边缘候选点丢失了一个。且使用该方法计算的图像的梯度只是考虑单个像素的差值,并没有利用到图像的像素的邻域特性。考虑到每个像素的某个邻域的灰度变化。因此,通常不会简单的利用梯度的定义进行梯度的计算,而是在像素的某个邻域内设置梯度算子。
考虑,3X3区域的像素,使用如下矩阵表示:
$$
\left[ \begin{array}{lll}{z_{1}} & {z_{2}} & {z_{3}} \\ {z_{4}} & {z_{5}} & {z_{6}} \\ {z_{7}} & {z_{8}} & {z_{9}}\end{array}\right]
$$
令中心点表示图像中任一像素,那么根据梯度的定义,其在x和y方向的梯度分别为:$g_{x}=z_{9}-z_{5}$和$g_{y}=z_{8}-z_{6}$,梯度图像
$$
M(x, y) \approx\left|z_{9}-z_{5}\right|+\left|z_{8}-z_{6}\right|
$$
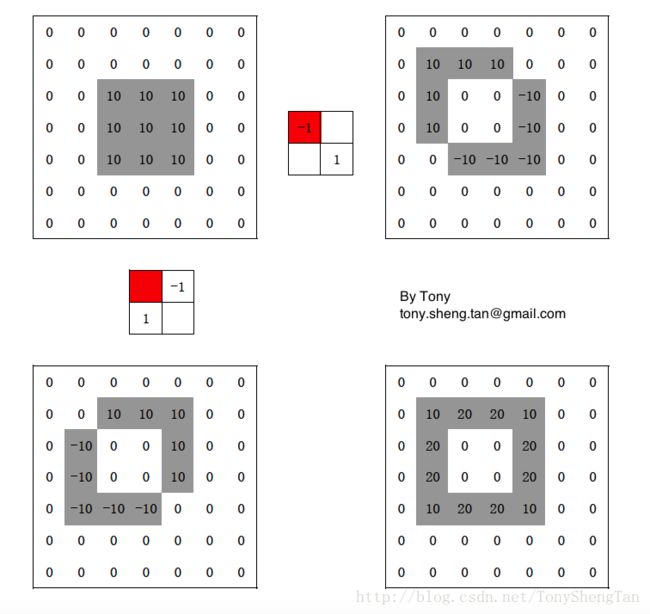
根据上述公式,Robert在1965年提出的Robert交叉算子
$$
\left[ \begin{array}{cc}{-1} & {0} \\ {0} & {1}\end{array}\right] \text { and } \left[ \begin{array}{cc}{0} & {-1} \\ {1} & {0}\end{array}\right]
$$
以下是一组Robort算子计算边界的示例,可以帮助你对Robort算子进行理解:
示例:
//实现直方图的反向投影
#include "stdafx.h"
#include
#include
#include
#include
#include
#include
using namespace cv;
using namespace std;
void robert_grad(const Mat& src, Mat &dst)
{
Mat grad_x, grad_y;
Mat kernel_x = (Mat_(2, 2) << -1, 0, 0, 1);
Mat kernel_y = (Mat_(2, 2) << 0, -1, 1, 0);
filter2D(src, grad_x, CV_32F, kernel_x);
filter2D(src, grad_y, CV_32F, kernel_y);
//convertScaleAbs(grad_x, grad_x);
//convertScaleAbs(grad_y, grad_y);
//addWeighted(grad_x, 1, grad_y, 1, 0, dst);
magnitude(grad_x, grad_y, dst);
convertScaleAbs(dst, dst);
}
int main()
{
Mat srcImage = imread("111.jpg",0);
if (!srcImage.data)
{
cout << "图像打开失败!" << endl;
return -1;
}
Mat robort_Img;
robert_grad(srcImage, robort_Img);
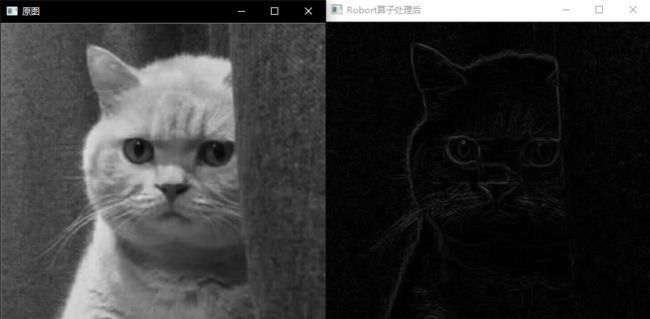
imshow("原图", srcImage);
imshow("Robort算子处理后", robort_Img);
waitKey();
return 0;
}
2、Sobel算子
Robert交叉算子的尺寸是偶数,偶数尺寸滤波器没有对称中心计算效率较低,所以通常滤波器的模板尺寸是奇数。
则有:
$$
\begin{aligned} g_{x} &=\left(z_{7}+2 z_{8}+z_{9}\right)-\left(z_{1}+2 z_{2}+z_{3}\right) \\ g_{y} &=\left(z_{3}+2 z_{0}+z_{9}\right)-\left(z_{1}+2 z_{4}+z_{7}\right) \end{aligned}
$$
利用上述公式可以得到如下两个卷积模板,分别计算图像在x和y方向的梯度
$$
\left[ \begin{array}{ccc}{-1} & {-2} & {-1} \\ {0} & {0} & {0} \\ {1} & {2} & {1}\end{array}\right]
$$
和
$$
\left[ \begin{array}{rrr}{-1} & {0} & {1} \\ {-2} & {0} & {2} \\ {-1} & {0} & {1}\end{array}\right]
$$
算法的相关实现如下所示:
bool Sobel(const Mat& image, Mat& result, int TYPE)
{
if (image.channels() != 1)
return false;
// 系数设置
int kx(0);
int ky(0);
if (TYPE == 0) {
kx = 0; ky = 1;
}
else if (TYPE == 1) {
kx = 1; ky = 0;
}
else if (TYPE == 2) {
kx = 1; ky = 1;
}
else
return false;
// 设置mask
float mask[3][3] = { {1,2,1},{0,0,0},{-1,-2,-1} };
Mat y_mask = Mat(3, 3, CV_32F, mask) / 8;
Mat x_mask = y_mask.t(); // 转置
// 计算x方向和y方向上的滤波
Mat sobelX, sobelY;
filter2D(image, sobelX, CV_32F, x_mask);
filter2D(image, sobelY, CV_32F, y_mask);
sobelX = abs(sobelX);
sobelY = abs(sobelY);
// 梯度图
Mat gradient = kx * sobelX.mul(sobelX) + ky * sobelY.mul(sobelY);
// 计算阈值
int scale = 4;
double cutoff = scale * mean(gradient)[0];
result.create(image.size(), image.type());
result.setTo(0);
for (int i = 1; i < image.rows - 1; i++)
{
float* sbxPtr = sobelX.ptr(i);
float* sbyPtr = sobelY.ptr(i);
float* prePtr = gradient.ptr(i - 1);
float* curPtr = gradient.ptr(i);
float* lstPtr = gradient.ptr(i + 1);
uchar* rstPtr = result.ptr(i);
// 阈值化和极大值抑制
for (int j = 1; j < image.cols - 1; j++)
{
if (curPtr[j] > cutoff && (
(sbxPtr[j] > kx*sbyPtr[j] && curPtr[j] > curPtr[j - 1] && curPtr[j] > curPtr[j + 1]) ||
(sbyPtr[j] > ky*sbxPtr[j] && curPtr[j] > prePtr[j] && curPtr[j] > lstPtr[j])))
rstPtr[j] = 255;
}
}
return true;
} 这里的非极大抑制Non-maximum suppression,这一步的目的是将模糊(blurred)的边界变得清晰(sharp)。通俗的讲,就是保留了每个像素点上梯度强度的极大值,而删掉其他的值。
示例:
//实现直方图的反向投影
#include "stdafx.h"
#include
#include
#include
#include
#include
#include
using namespace cv;
using namespace std;
bool Sobel(const Mat& image, Mat& result, int TYPE)
{
if (image.channels() != 1)
return false;
// 系数设置
int kx(0);
int ky(0);
if (TYPE == 0) {
kx = 0; ky = 1;
}
else if (TYPE == 1) {
kx = 1; ky = 0;
}
else if (TYPE == 2) {
kx = 1; ky = 1;
}
else
return false;
// 设置mask
float mask[3][3] = { {1,2,1},{0,0,0},{-1,-2,-1} };
Mat y_mask = Mat(3, 3, CV_32F, mask) / 8;
Mat x_mask = y_mask.t(); // 转置
// 计算x方向和y方向上的滤波
Mat sobelX, sobelY;
filter2D(image, sobelX, CV_32F, x_mask);
filter2D(image, sobelY, CV_32F, y_mask);
sobelX = abs(sobelX);
sobelY = abs(sobelY);
// 梯度图
Mat gradient = kx * sobelX.mul(sobelX) + ky * sobelY.mul(sobelY);
// 计算阈值
int scale = 4;
double cutoff = scale * mean(gradient)[0];
result.create(image.size(), image.type());
result.setTo(0);
for (int i = 1; i < image.rows - 1; i++)
{
float* sbxPtr = sobelX.ptr(i);
float* sbyPtr = sobelY.ptr(i);
float* prePtr = gradient.ptr(i - 1);
float* curPtr = gradient.ptr(i);
float* lstPtr = gradient.ptr(i + 1);
uchar* rstPtr = result.ptr(i);
// 阈值化和极大值抑制
for (int j = 1; j < image.cols - 1; j++)
{
if (curPtr[j] > cutoff && (
(sbxPtr[j] > kx*sbyPtr[j] && curPtr[j] > curPtr[j - 1] && curPtr[j] > curPtr[j + 1]) ||
(sbyPtr[j] > ky*sbxPtr[j] && curPtr[j] > prePtr[j] && curPtr[j] > lstPtr[j])))
rstPtr[j] = 255;
}
}
return true;
}
int main()
{
Mat srcImage = imread("111.jpg",0);
if (!srcImage.data)
{
cout << "图像打开失败!" << endl;
return -1;
}
Mat sobel_x_Img, sobel_y_Img, sobel_xy_Img;
blur(srcImage, srcImage, Size(5, 5), Point(-1, -1));//由于直接滤波效果不好,这里用均值滤波滤除噪点
Sobel(srcImage, sobel_x_Img,0);
Sobel(srcImage, sobel_y_Img, 1);
Sobel(srcImage, sobel_xy_Img, 2);
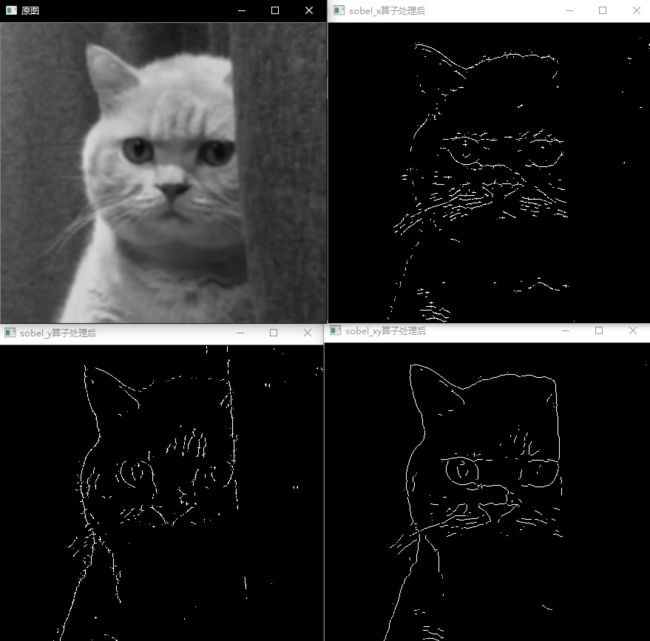
imshow("原图", srcImage);
imshow("sobel_x算子处理后", sobel_x_Img);
imshow("sobel_y算子处理后", sobel_y_Img);
imshow("sobel_xy算子处理后", sobel_xy_Img);
waitKey();
return 0;
}
程序运行效果如下:
同样的,OpenCV提供了Sobel算子的API函数
Sobel(
InputArray Src // 输入图像
OutputArray dst// 输出图像,大小与输入图像一致
int depth // 输出图像深度.
Int dx. // X方向,几阶导数
int dy // Y方向,几阶导数.
int ksize, SOBEL算子kernel大小,必须是1、3、5、7、
double scale = 1
double delta = 0
int borderType = BORDER_DEFAULT
)
示例如下:
#include "stdafx.h"
#include
#include
using namespace std;
using namespace cv;
//边缘检测
int main()
{
Mat img = imread("111.jpg");
imshow("原始图", img);
Mat grad_x, grad_y;
Mat abs_grad_x, abs_grad_y, dst;
//求x方向梯度
Sobel(img, grad_x, CV_16S, 1, 0, 3, 1, 1, BORDER_DEFAULT);
convertScaleAbs(grad_x, abs_grad_x);
imshow("x方向soble", abs_grad_x);
//求y方向梯度
Sobel(img, grad_y, CV_16S, 0, 1, 3, 1, 1, BORDER_DEFAULT);
convertScaleAbs(grad_y, abs_grad_y);
imshow("y向soble", abs_grad_y);
//合并梯度
addWeighted(abs_grad_x, 0.5, abs_grad_y, 0.5, 0, dst);
imshow("整体方向soble", dst);
waitKey(0);
}
程序运行结果如下:
3、基于二阶微分的算子
1、Laplacian算子
二阶微分算子的代表就是拉普拉斯算子,其定义如下:
$$
\nabla^{2} f=\frac{\partial^{2} f}{\partial x^{2}}+\frac{\partial^{2} f}{\partial y^{2}}
$$
其中:
$$
\begin{aligned} \frac{\partial^{2} f}{\partial x^{2}} &=f(x+1, y)+f(x-1, y)-2 f(x, y) \\ \frac{\partial^{2} f}{\partial y^{2}} &=f(x, y+1)+f(x, y-1)-2 f(x, y) \end{aligned}
$$
对于上述的3X3区域,则有
$$
\nabla^{2} f=z_{2}+z_{4}+z_{6}+z_{8}-4 z_{5}
$$
其得到的模板如下:
$$
\left[ \begin{array}{ccc}{0} & {1} & {0} \\ {1} & {-4} & {1} \\ {0} & {1} & {0}\end{array}\right]
$$
因为在锐化增强中,绝对值相同的正值和负值实际上表示相同的响应,故也等同于使用模板
$$
\left[ \begin{array}{ccc}{0} & {-1} & {0} \\ {-1} & {4} & {-1} \\ {0} & {-1} & {0}\end{array}\right]
$$
分析模板结构,可知模板对于90°的旋转是各向同性的。所谓对于某角度各向同性是指把原图像旋转该角度后在进行滤波与对原图像滤波在旋转该角度的结果相同。这说明laplacian算子对于接近水平和接近竖直放i想的边缘都有很好的增强,从而避免了在使用梯度算子时要进行多次滤波的麻烦。更进一步,我们还可以得到45°旋转各向同性的滤波器:
$$
W_{3}=\left[ \begin{array}{ccc}{1} & {1} & {1} \\ {1} & {-8} & {1} \\ {1} & {1} & {1}\end{array}\right]
$$
和
$$
W_{4}=\left[ \begin{array}{ccc}{-1} & {-1} & {-1} \\ {-1} & {8} & {-1} \\ {-1} & {-1} & {-1}\end{array}\right]
$$
沿用高斯平滑的思想,根据到中心点的距离给模板周边的点赋予不同的权重,还可得到如下模板:
$$
W_{5}=\left[ \begin{array}{ccc}{1} & {4} & {1} \\ {4} & {-20} & {4} \\ {1} & {4} & {1}\end{array}\right]
$$
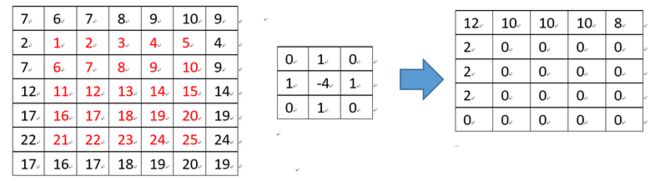
在OpenCV中默认的计算方式如下,假设有一个5*5的小图像,原始值依次为1,2,…25,如下图红色部分,首先将5*5映射到(5+3-1)*(5+3-1)大小,然后和3*3的kernel做累积和,因为计算结果有可能超出有效值[0, 255]范围,因此在最终还需要判断使其在有效范围内,即小于0为0,大于255为255:
如坐标为(0,0)的计算过程为:12 = 7*0+6*1+7*0+2*1+1*(-4)+2*1+7*0+6*1+7*0.
OpenCV提供的Laplacian的函数API为:
Laplacian( src_gray, dst, ddepth, kernel_size, scale, delta, BORDER_DEFAULT );
参数意义为,
- src_gray,输入图像
- dst,Laplace操作结果
- ddepth,输出图像深度,因为输入图像一般为CV_8U,为了避免数据溢出,输出图像深度应该设置为CV_16S
- 滤波器孔径尺寸;
- 比例因子;
- 表示结果存入目标图
示例
#include "stdafx.h"
#include
#include
using namespace std;
using namespace cv;
//边缘检测
int main()
{
Mat img = imread("111.jpg");
imshow("原始图", img);
Mat gray, dst, abs_dst;
//转换为灰度图
cvtColor(img, gray, COLOR_RGB2GRAY);
//使用Laplace函数
//第三个参数:目标图像深度;第四个参数:滤波器孔径尺寸;第五个参数:比例因子;第六个参数:表示结果存入目标图
Laplacian(gray, dst, CV_16S, 3, 1, 0, BORDER_DEFAULT);
//计算绝对值,并将结果转为8位
convertScaleAbs(dst, abs_dst);
waitKey(0);
}
2、Log算子
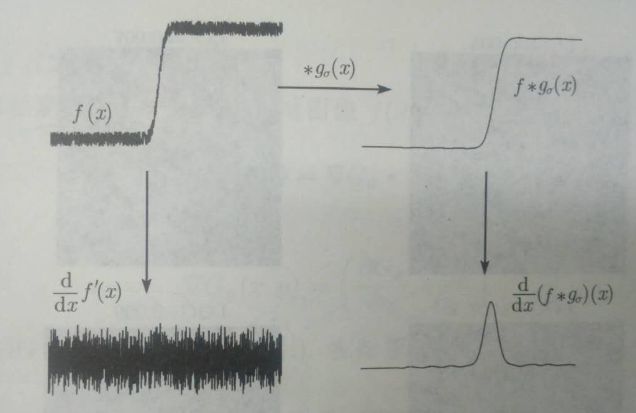
1980年,Marr和Hildreth提出将Laplace算子与高斯低通滤波相结合,提出了LOG(Laplace and Guassian)算子。
高斯函数和一级、二阶导数如下图所示:
![]()
步骤如下:
1.对图像先进性高斯滤波(G × f),再进行Laplace算子运算Δ(G × f);
2.保留一阶导数峰值的位置,从中寻找Laplace过零点;
3.对过零点的精确位置进行插值估计。寻找Laplace零点的原因是如果图像中有噪声,噪声在一阶导数处也会取得极大值从而被当作边缘。然而求解这个极大值也不方便,采用二阶导数后,极大值点就为0了,因此值为0的地方就是边界。
由上图可以看出,高斯滤波之后边缘信息才显现出来。
LOG算子如下:
$$
\nabla^{2} G=\frac{\partial^{2} G}{\partial x^{2}}+\frac{\partial^{2} G}{\partial y^{2}}=\frac{-2 \sigma^{2}+x^{2}+y^{2}}{2 \pi \sigma^{6}} e^{-\left(x^{2}+y^{2}\right) / 2 \sigma^{2}}
$$
常用模板如下:
![]()
示例:
在OpenCV中实现Log算子的方法如下:
#include "stdafx.h"
#include
#include "opencv2/imgproc/imgproc.hpp"
#include
int main()
{
cv::Mat srcImage =
cv::imread("111.jpg", 0);
if (!srcImage.data)
return -1;
// 高斯平滑
GaussianBlur(srcImage, srcImage, cv::Size(3, 3),
0, 0, cv::BORDER_DEFAULT);
cv::Mat dstImage;
// 拉普拉斯变换
Laplacian(srcImage, dstImage, CV_16S, 3);
convertScaleAbs(dstImage, dstImage);
cv::imshow("srcImage", srcImage);
cv::imshow("dstImage", dstImage);
cv::waitKey(0);
return 0;
}
4、导向滤波
导向图滤波主要是通过一张引导图G,对目标图像P(输入图像)进行滤波处理,使得最后的输出图像大体上与目标图像P相似,但是纹理部分与引导图G相似。导向滤波不仅能够实现双边滤波的边缘平滑,而且在检测到边缘附近有很好的表现,可以应用在图像增强、HDR压缩、图像抠图以及图像去雾等场景中。
导向滤波的实现原理如下:
对于普通的线性变换滤波器,输入图像是I,输出图像是S,导向函数为T,导向滤波定义在像素点j处的滤波结果可以表示为下式:
$$
S_{j}=\sum_{i} W_{i j}(T) I_{j}
$$
其中,i,j是图像像素的下标,滤波器核函数Wij是图像的加权系数,景点的双边滤波器核给定如下:
$$
W_{i j}^{b f}(I)=\frac{1}{K_{i}} \exp \left(-\frac{\left|x_{i}-x_{j}\right|^{2}}{\sigma_{s}^{2}}\right) \exp \left(-\frac{\left|I_{i}-I_{j}\right|^{2}}{\sigma_{r}^{2}}\right)
$$
其中x是像素坐标Ki是一个归一化参数
$$
\sum_{i} W_{i j}^{b f}=1
$$
参数σs和σr代表空间相似度以及颜色范围相似度的灵敏性
假设导向滤波器存在线性模型如下:
$$
s_{i}=a_{k} I_{i}+b_{k} \quad i \in W_{k}
$$
其中窗口函数Wk是S以I为中心在像素k位置形成的线性变换,叙述ak和bk满足相同的线性系数,为确定线性系数,定义的输出相应q应满足下式:
$$
q_{i}=I_{i}-n_{i}
$$
其中ni表示噪声,局部线性模型确定输入与输出相应的边缘,就可以最小化q与I之间的差异,同事保持原线性变换。
最小化窗口函数Wk:
$$
E\left(a_{k}, b_{k}\right)=\sum_{i \in w k}\left(\left(a_{k} I_{i}+b_{k}-p_{i}\right)^{2}+\psi a_{k}^{2}\right)
$$
其中Ψ是一个正则化参数,根据线性变换得到系数ak和bk:
$$
\begin{array}{l}{a_{k}=\frac{\frac{1}{|w|} \sum_{i \in w k} T_{i} I_{i}-\mu_{i} \overline{I_{k}}}{\sigma_{k}^{2}+\psi}} \\ {b_{k}=\overline{I_{k}}-a_{k} \mu_{k}}\end{array}
$$
其中μk与σk是导向图像I的窗口wk的均值和方差,|w|是像素的总个数,
$$
\overline{I_{k}}=\frac{1}{|w|} \sum_{i \in w k} I_{i}
$$
导向滤波实现步骤如下:
(1.利用boxFilter滤波器完成均值计算,其中均值包括导向均值、原始均值、互相关均值以及自相关均值
(2.根据均值计算相关系数参数,包括自相关与互相关方差。
(3.计算窗口线性变换参数系数a、b。
(4.根据公式计算参数a、b的均值。
(5.利用参数得到导向滤波输出矩阵S。
用程序表示如下所示:
Mat guidedfilter(Mat &srcImage, Mat &srcClone, int r, double eps)
{
//转换源图像信息
srcImage.convertTo(srcImage, CV_64FC1);
srcClone.convertTo(srcClone, CV_64FC1);
int NumRows = srcImage.rows;
int NumCols = srcImage.cols;
Mat boxResult;
//下面按照步骤进行导向滤波操作
/
//步骤一:计算均值
boxFilter(Mat::ones(NumRows, NumCols, srcImage.type()),
boxResult, CV_64FC1, Size(r, r));
//生成导向均值mean_I
Mat mean_I;
boxFilter(srcImage, mean_I, CV_64FC1, Size(r, r));
//生成原始均值mean_P
Mat mean_P;
boxFilter(srcClone, mean_P, CV_64FC1, Size(r, r));
//生成互相关均值mean_IP
Mat mean_IP;
boxFilter(srcImage.mul(srcClone), mean_IP,
CV_64FC1, Size(r, r));
Mat cov_IP = mean_IP - mean_I.mul(mean_P);
//生成自相关均值mean_II
Mat mean_II;
//应用盒滤波计算相关均值
boxFilter(srcImage.mul(srcImage), mean_II, CV_64FC1, Size(r, r));
//步骤二:计算相关系数
Mat var_I = mean_II - mean_I.mul(mean_I);
Mat var_IP = mean_IP - mean_I.mul(mean_P);
//步骤三:计算参数系数a,b
Mat a = cov_IP / (var_I + eps);
Mat b = mean_P = a.mul(mean_I);
//步骤四:计算系数a,b的均值
Mat mean_a;
boxFilter(a, mean_a, CV_64FC1, Size(r, r));
mean_a = mean_a / boxResult;
Mat mean_b;
boxFilter(b, mean_b, CV_64FC1, Size(r, r));
mean_b = mean_b / boxResult;
//步骤五:生成输出矩阵
Mat resultMat = mean_a.mul(srcImage) + mean_b;
return resultMat;
}
示例:
#include "stdafx.h"
#include
#include
#include
#include
using namespace cv;
using namespace std;
//导向滤波器
Mat guidedfilter(Mat &srcImage, Mat &srcClone, int r, double eps);
int main()
{
Mat srcImage = imread("111.jpg");
if (srcImage.empty())
{
cout << "读入图片错误!" << endl;
system("pause");
return -1;
}
//进行通道分离
vectorvSrcImage, vResultImage;
split(srcImage, vSrcImage);
Mat resultMat;
for (int i = 0; i < 3; i++)
{
//分通道转换成浮点型数据
Mat tempImage;
vSrcImage[i].convertTo(tempImage, CV_64FC1, 1.0 / 255.0);
Mat p = tempImage.clone();
//分别进行导向滤波
Mat resultImage = guidedfilter(tempImage, p, 4, 0.01);
vResultImage.push_back(resultImage);
}
//通道结果合并
merge(vResultImage, resultMat);
imshow("原图像", srcImage);
imshow("导向滤波后图像", resultMat);
waitKey(0);
return 0;
}
Mat guidedfilter(Mat &srcImage, Mat &srcClone, int r, double eps)
{
//转换源图像信息
srcImage.convertTo(srcImage, CV_64FC1);
srcClone.convertTo(srcClone, CV_64FC1);
int NumRows = srcImage.rows;
int NumCols = srcImage.cols;
Mat boxResult;
//下面按照步骤进行导向滤波操作
/
//步骤一:计算均值
boxFilter(Mat::ones(NumRows, NumCols, srcImage.type()),
boxResult, CV_64FC1, Size(r, r));
//生成导向均值mean_I
Mat mean_I;
boxFilter(srcImage, mean_I, CV_64FC1, Size(r, r));
//生成原始均值mean_P
Mat mean_P;
boxFilter(srcClone, mean_P, CV_64FC1, Size(r, r));
//生成互相关均值mean_IP
Mat mean_IP;
boxFilter(srcImage.mul(srcClone), mean_IP,
CV_64FC1, Size(r, r));
Mat cov_IP = mean_IP - mean_I.mul(mean_P);
//生成自相关均值mean_II
Mat mean_II;
//应用盒滤波计算相关均值
boxFilter(srcImage.mul(srcImage), mean_II, CV_64FC1, Size(r, r));
//步骤二:计算相关系数
Mat var_I = mean_II - mean_I.mul(mean_I);
Mat var_IP = mean_IP - mean_I.mul(mean_P);
//步骤三:计算参数系数a,b
Mat a = cov_IP / (var_I + eps);
Mat b = mean_P = a.mul(mean_I);
//步骤四:计算系数a,b的均值
Mat mean_a;
boxFilter(a, mean_a, CV_64FC1, Size(r, r));
mean_a = mean_a / boxResult;
Mat mean_b;
boxFilter(b, mean_b, CV_64FC1, Size(r, r));
mean_b = mean_b / boxResult;
//步骤五:生成输出矩阵
Mat resultMat = mean_a.mul(srcImage) + mean_b;
return resultMat;
}
5、canny算子——边缘检测方法的提出
Canny算子是John F. Canny于 1986 年开发出来的一个多级边缘检测算法。Canny 的目标是找到一个最优的边缘检测算法,最优边缘检测的含义是:
-
应用高斯滤波来平滑图像,目的是去除噪声,任何边缘检测算法都不可能在未经处理的原始数据上很好地工作,所以第一步是对原始数据与高斯 mask 作 卷积,得到的图像与原始图像相比有些轻微的模糊(blurred)。
-
找寻图像的强度梯度(intensity gradients),即找寻一幅图像中灰度强度变化最强的位置。
-
应用非最大抑制(non-maximum suppression)技术来消除边误检(本来不是但检测出来是)。就是保留了每个像素点上梯度强度的极大值,而删掉其他的值。
-
应用双阈值的方法来决定可能的(潜在的)边界
-
利用滞后技术来跟踪边界
非最大抑制
非最大抑制的目的是将模糊(blurred)的边界变得清晰(sharp)。通俗的讲,就是保留了每个像素点上梯度强度的极大值,而删掉其他的值。对于每个像素点,进行如下操作:

图中的数字代表了像素点的梯度强度,箭头方向代表了梯度方向。以第二排第三个像素点为例,由于梯度方向向上,则将这一点的强度(7)与其上下两个像素点的强度(5和4)比较,由于这一点强度最大,则保留。
双阈值
双阈值的技术即设定一个阈值上界和阈值下界(opencv中通常由人为指定的),图像中的像素点如果大于阈值上界则认为必然是边界(称为强边界,strong edge),小于阈值下界则认为必然不是边界,两者之间的则认为是候选项(称为弱边界,weak edge),需进行进一步处理。
滞后技术
滞后技术即将和强边界相连的弱边界认为是边界,其他的弱边界则被抑制。
OpenCV提供了对应的Canny算子的API函数,函数如下所示:
void Canny(inputArray,outputArray,double threshold1,double threshold2,int apertureSize=3,bool L2gradient=false)
*第一个参数,输入图像,且需为单通道8位图像。
*第二个参数,输出的边缘图。
*第三个参数,第一个滞后性阈值。用于边缘连接。
*第四个参数,第二个滞后性阈值。用于控制强边缘的初始段,高低阈值比在2:1到3:1之间。
*第五个参数,表明应用sobel算子的孔径大小,默认值为3。
*第六个参数,bool类型L2gradient,一个计算图像梯度幅值的标识,默认值false。示例:
#include "stdafx.h"
#include
#include
#include
#include
#include"math.h"
using namespace std;
using namespace cv;
Mat Img_in, Img_gray, Img_out,Img_canny;
Mat scr;
int main()
{
Img_in = imread("111.jpg");
int rows = Img_in.rows;
int cols = Img_in.cols;//获取图像尺寸
cvtColor(Img_in, Img_gray, CV_BGR2GRAY);
imshow("【灰度图】", Img_gray);//转化为灰度图
//step1:高斯平滑
Mat img_filt;
GaussianBlur(Img_gray, Img_out, Size(3, 3), 0, 0);
Canny(Img_out, Img_canny, 50, 150, 3);
imshow("自带函数结果", Img_canny);
//adaptiveThreshold(img_filt , Img_out , 255 ,ADAPTIVE_THRESH_MEAN_C , THRESH_BINARY,min(rows,cols), 0);
//imshow("【二值图】",Img_out );
Img_out.convertTo(Img_out, CV_32FC1); //将图像转换为float或double型,否则算梯度会报错
/*step2:计算梯度(幅度和方向)
选择一阶差分卷积模板:
dx=[-1,-1;1,1] dy=[1,-1;1,-1]
*/
Mat gy = (Mat_(2, 2) << 1, -1,
1, -1);
//定义一阶差分卷积梯度模板
Mat gx = (Mat_(2, 2) << -1, -1,
1, 1); //定义一阶差分卷积梯度模板
Mat img_gx, img_gy, img_g;//定义矩阵
Mat img_dir = Mat::zeros(rows, cols, CV_32FC1);//定义梯度方向矩阵,计算角度为float型
filter2D(Img_out, img_gx, Img_out.depth(), gx); //获取x方向的梯度图像.使用梯度模板进行二维卷积,结果与原图像大小相同
filter2D(Img_out, img_gy, Img_out.depth(), gy); //获取x方向的梯度图像.使用梯度模板进行二维卷积,结果与原图像大小相同
img_gx = img_gx.mul(img_gx);//点乘(每个像素值平方)
img_gy = img_gy.mul(img_gy);//点乘(每个像素值平方)
img_g = img_gx + img_gy;
sqrt(img_g, img_g); //梯度幅值图像
imshow("梯度图", img_g);
//求梯度方向图像
for (int i = 0; i < rows; i++)
{
for (int j = 0; j < cols; j++)
{
img_dir.at(i, j) = fastAtan2(img_gy.at(i, j), img_gx.at(i, j));//求角度
}
}
/* step3:对梯度幅值进行非极大值抑制
首先将角度划分成四个方向范围:水平(0°)、45°、垂直(90°)、135°
*/
Mat Nms = Mat::zeros(rows, cols, CV_32FC1);//定义一个非极大值抑制图像,float型
for (int i = 0; i < rows; i++)
{
for (int j = 0; j < cols; j++)
{
if (img_dir.at(i, j) <= 22.5 && img_dir.at(i, j) >= 0 || img_dir.at(i, j) >= 157.5 && img_dir.at(i, j) <= 202.5
|| img_dir.at(i, j) >= 337.5 && img_dir.at(i, j) <= 360)
img_dir.at(i, j) = 0;
else if (img_dir.at(i, j) > 22.5 && img_dir.at(i, j) <= 67.5 || img_dir.at(i, j) > 202.5 && img_dir.at(i, j) <= 247.5)
img_dir.at(i, j) = 45;
else if (img_dir.at(i, j) > 67.5 && img_dir.at(i, j) <= 112.5 || img_dir.at(i, j) > 247.5 && img_dir.at(i, j) <= 292.5)
img_dir.at(i, j) = 90;
else if (img_dir.at(i, j) > 112.5 && img_dir.at(i, j) < 157.5 || img_dir.at(i, j) > 292.5 && img_dir.at(i, j) < 337.5)
img_dir.at(i, j) = 135;
}
}
for (int i = 1; i < rows - 1; i++)
{
for (int j = 1; j < cols - 1; j++)
{
if (img_dir.at(i, j) == 90 && img_g.at(i, j) == max(img_g.at(i, j), max(img_g.at(i, j + 1), img_g.at(i, j - 1))))
Nms.at(i, j) = img_g.at(i, j);
else if (img_dir.at(i, j) == 45 && img_g.at(i, j) == max(img_g.at(i, j), max(img_g.at(i - 1, j + 1), img_g.at(i + 1, j - 1))))
Nms.at(i, j) = img_g.at(i, j);
else if (img_dir.at(i, j) == 0 && img_g.at(i, j) == max(img_g.at(i, j), max(img_g.at(i - 1, j), img_g.at(i + 1, j))))
Nms.at(i, j) = img_g.at(i, j);
else if (img_dir.at(i, j) == 135 && img_g.at(i, j) == max(img_g.at(i, j), max(img_g.at(i - 1, j - 1), img_g.at(i + 1, j + 1))))
Nms.at(i, j) = img_g.at(i, j);
}
}
/*step4:双阈值检测和连接边缘
*/
Mat img_dst = Mat::zeros(rows, cols, CV_32FC1);//定义一个双阈值图像,float型
double TH, TL;
double maxVal = 0;//必须为double类型,且必须赋初值,否则报错
Nms.convertTo(Nms, CV_64FC1); //为了计算,将非极大值抑制图像转为double型
minMaxLoc(Nms, NULL, &maxVal, NULL, NULL); //求矩阵 Nms最大值
TH = 0.5*maxVal;//高阈值
TL = 0.3*maxVal;//低阈值
for (int i = 0; i < rows; i++)
{
for (int j = 0; j < cols; j++)
{
if (Nms.at(i, j) < TL)
img_dst.at(i, j) = 0;
else if (Nms.at(i, j) > TH)
img_dst.at(i, j) = 1;
else if (Nms.at(i - 1, j - 1) < TL || Nms.at(i - 1, j) < TL || Nms.at(i - 1, j + 1) < TL ||
Nms.at(i, j - 1) < TL || Nms.at(i, j + 1) < TL || Nms.at(i + 1, j - 1) < TL ||
Nms.at(i + 1, j) < TL || Nms.at(i + 1, j + 1) < TL)
img_dst.at(i, j) = 1;
}
}
imshow("非极大值抑制图", Nms);
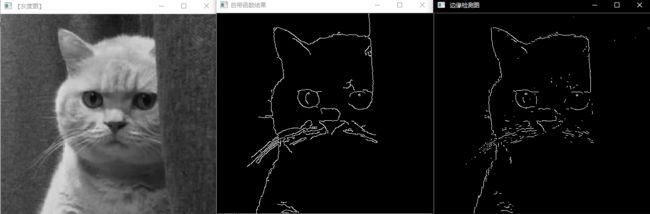
imshow(" 边缘检测图", img_dst);
imwrite(" 边缘检测效果图.jpg", img_dst);//保存图像
waitKey(0);
return 0;
}