弗洛伊德算法和迪杰斯特拉算法解决最短路径问题

弗洛伊德算法

算法介绍

算法图解分析 

 

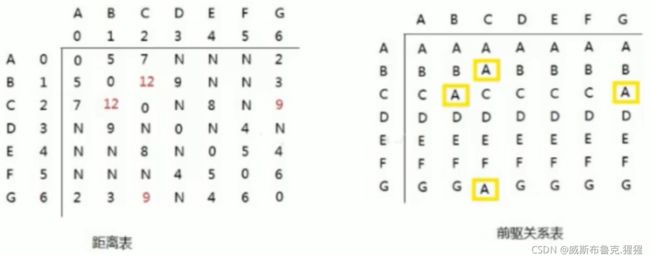
 第一轮循环中，以A(下标为：0)作为中间顶点【即把作为中间顶点的所有情况都进行遍历，就会得到更新距离表和前驱关系】，距离表和前驱关系更新为：

弗洛伊德算法和迪杰斯特拉算法的最大区别是：弗洛伊德算法是从各个顶点出发，求最短路径；迪杰斯特拉算法是从某个顶点开始，求最短路径。 

/**
	 * 弗洛伊德算法
	 * 容易理解，容易实现
	 */
	public void floyd() {
		int len = 0;//变量保存距离
		//对中间顶点遍历，k就是中间顶点的下标[A,B,C,D,E,F,G]
		for(int k = 0;k < dis.length;k++) {
			//从i顶点开始出发[A,B,C,D,E,F,G]
			for(int i = 0;i < dis.length;i++) {
				//到达j顶点 //[A,B,C,D,E,F,G]
				for(int j = 0;j < dis.length;j++) {
					len = dis[i][k] + dis[k][j];//=>求出从i顶点出发，经过k中间顶点，到达j顶点距离
					if(len < dis[i][j]) {//如果len小于dis[i][j]
						dis[i][j] = len;//更新距离
						pre[i][j] = pre[k][j];//更新前驱顶点
					}
				}
			}
		}
	}

迪杰斯特拉算法

 

算法介绍

算法过程 

public class DijkstraAlgorithm {
	public static void main(String[] args) {
		char[] vertex = { 'A', 'B', 'C', 'D', 'E', 'F', 'G' };
		// 邻接矩阵
		int[][] matrix = new int[vertex.length][vertex.length];
		final int N = 65535;// 表示不可以连接
		matrix[0] = new int[] { N, 5, 7, N, N, N, 2 };
		matrix[1] = new int[] { 5, N, N, 9, N, N, 3 };
		matrix[2] = new int[] { 7, N, N, N, 8, N, N };
		matrix[3] = new int[] { N, 9, N, N, N, 4, N };
		matrix[4] = new int[] { N, N, 8, N, N, 5, 4 };
		matrix[5] = new int[] { N, N, N, 4, 5, N, 6 };
		matrix[6] = new int[] { 2, 3, N, N, 4, 6, N };
		// 创建Graph对象
		Graph graph = new Graph(vertex, matrix);
		// 测试，图的邻接矩阵是否ok
		graph.showGraph();
		// 测试迪杰斯特拉算法
		graph.dsj(6);
		graph.showDijkstra();
	}
}

class Graph {
	private char[] vertex;// 顶点数组
	private int[][] matrix;// 邻接矩阵
	private VisitedVertex vv;// 已经访问过的顶点的集合

	// 构造器
	public Graph(char[] vertex, int[][] matrix) {
		this.vertex = vertex;
		this.matrix = matrix;
	}

	// 显示结果
	public void showDijkstra() {
		vv.show();
	}

	// 显示图
	public void showGraph() {
		for (int[] link : matrix) {
			System.out.println(Arrays.toString(link));
		}
	}

	/**
	 * 迪杰斯特拉算法实现
	 * 
	 * @param index 表示出发顶点对应的下标
	 */
	public void dsj(int index) {
		vv = new VisitedVertex(vertex.length, index);
		update(index);// 更新index顶点到周围顶点的距离和前驱顶点
		for (int j = 1; j < vertex.length; j++) {
			index = vv.updateArr();// 选择并返回新的访问顶点
			update(index);// 更新index顶点到周围顶点的距离和前驱顶点
		}
	}

	/**
	 * 更新index下标顶点到周围顶点的距离和周围顶点的前驱顶点
	 */
	private void update(int index) {
		int len = 0;
		// 根据遍历邻接矩阵的 matrix[index]行
		for (int j = 0; j < matrix[index].length; j++) {
			// len含义是：出发顶点到index顶点的距离 + 从index顶点到j顶点的距离的和
			len = vv.getDis(index) + matrix[index][j];
			// 如果j顶点没有被访问过，并且len小于出发顶点到j顶点的距离，就需要更新
			if (!vv.in(j) && len < vv.getDis(j)) {
				vv.updateDis(j, index);// 更新j顶点的前驱为index顶点
				vv.updateDis(j, len);// 更新出发顶点到j顶点的距离
			}
		}
	}
}

//已访问顶点集合
class VisitedVertex {
	// 记录各个顶点是否访问过; 1表示访问过，0未访问，会动态更新
	public int[] already_arr;
	// 每个下标对应的值为前一个顶点下标，会动态更新
	public int[] pre_visited;
	// 记录出发顶点到其他所有顶点的距离，比如G为出发顶点，就会记录G到其他顶点的距离，动态更新，求的最短距离放到dis
	public int[] dis;

	/**
	 * 构造器
	 * 
	 * @param length 表示顶点的个数
	 * @param index  出发顶点对应的下标，比如G顶点，下标就是6
	 */
	public VisitedVertex(int length, int index) {
		this.already_arr = new int[length];
		this.pre_visited = new int[length];
		this.dis = new int[length];
		// 初始化dis数组
		Arrays.fill(dis, 65535);
		this.already_arr[index] = 1;// 设置出发顶点被访问过
		this.dis[index] = 0;// 设置出发顶点的访问距离为0
	}

	/**
	 * 判断index顶点是否被访问过
	 * 
	 * @param index
	 * @return 如果访问过，就返回true,否则返回false
	 */
	public boolean in(int index) {
		return already_arr[index] == 1;
	}

	/**
	 * 更新出发顶点到index顶点的距离
	 * 
	 * @param index
	 * @param len
	 */
	public void updateDis(int index, int len) {
		dis[index] = len;
	}

	/**
	 * 更新pre这个顶点的前驱顶点为index顶点
	 * 
	 * @param pre
	 * @param index
	 */
	public void updatePre(int pre, int index) {
		pre_visited[pre] = index;
	}

	/**
	 * @return 返回出发顶点到index顶点的距离
	 */
	public int getDis(int index) {
		return dis[index];
	}

	public int updateArr() {
		int min = 65535, index = 0;
		for (int i = 0; i < already_arr.length; i++) {
			if (already_arr[i] == 0 && dis[i] < min) {
				min = dis[i];
				index = i;
			}
		}
		// 更新index顶点被访问过
		already_arr[index] = 1;
		return index;
	}

	// 显示最后的结果
	// 即将三个数组的情况输出
	public void show() {
		System.out.println("==========================");
		// 输出already_arr
		for (int i : already_arr) {
			System.out.print(i + " ");
		}
		// 输出pre_visited
		for (int i : pre_visited) {
			System.out.print(i + " ");
		}
		// 输出dis
		for (int i : dis) {
			System.out.print(i + " ");
		}
		System.out.println();
		// 为了好看最后的最短距离，如下处理
		char[] vertex = { 'A', 'B', 'C', 'D', 'E', 'F', 'G' };
		int count = 0;
		for (int i : dis) {
			if (i != 65535) {
				System.out.print(vertex[count] + "(" + i + ")");
			} else {
				System.out.println("N");
			}
			count++;
		}
		System.out.println();
	}
}