机器学习(优化算法一)——梯度下降
对于机器学习,经常提及的就是批量梯度下降、随机梯度下降,以及两者结合的小批量梯度下降。在深度学习中,常用的还有梯度下降的一些变种,像Adam、AdaGrad……这里只说最基本的三种。
简要过程
像普通线性回归、Ridge回归,通过求导,也就是最小二乘法就可以求解,但Lasso不可以,Lasso通常采用的是坐标轴下降法。除了最小二乘法,还有另外一种方法,也是最常用的:梯度下降法。
比如有一个函数
y = f ( x ) = x ² y=f(x)=x² y=f(x)=x²
对应的图

我们要求的是
x ∗ = arg min x y x^∗=\argmin \limits_x y x∗=xargminy
这里简单说一下梯度下降基本的原理:
比如先随机找一点 x 0 = 2 x_0=2 x0=2,此时 y 0 = 4 y_0=4 y0=4。而目标点是 (0,0) 这个点;
现在找一点 x 1 x_1 x1, x 1 x_1 x1 只有在 x 0 x_0 x0 的左侧,即 x 1 < x 0 x_1
接着再找 x 2 x_2 x2, x 2 x_2 x2 应位于 x 1 x_1 x1 的右侧,即 x 2 > x 1 x_2>x_1 x2>x1……
……
最终如上图,越来越接近目标点。也就我们基于递归的思想,每步都离目标更近一些。
对于 x 0 = 2 x_0=2 x0=2, y 0 ′ = 4 > 0 y_0^′=4>0 y0′=4>0,我们期望找到 x 1 = x 0 − ∆ 1 x_1=x_0-∆_1 x1=x0−∆1
假如现在找到了 x 1 = − 1.2 x_1=-1.2 x1=−1.2,此时 y 0 ′ = − 2.4 < 0 y_0^′=-2.4<0 y0′=−2.4<0,下一步则期望找到 x 2 = x 1 + ∆ 2 x_2=x_1+∆_2 x2=x1+∆2
我们不可能全部的∆ 都找出来。我们知道导数表示变化率,梯度表示的变化最快的情况,导数同时也是梯度在一维(这里说的是 x x x 的维度)空间的表现形式。我们当然是希望以最快的方式找到目标点,那么可不可以把梯度引入进来?
观察一下上面的内容,
对于 ∆ 1 ∆_1 ∆1,可以令他等于 ∆ ∗ y 0 ′ ∆∗y_0^′ ∆∗y0′,即 x 1 = x 0 − ∆ ∗ y 0 ′ x_1=x_0 − ∆∗y_0^′ x1=x0−∆∗y0′
对于 ∆ 2 ∆_2 ∆2,可以令他等于 ∆ ∗ y 1 ′ ∆∗y_1^′ ∆∗y1′,而 y 1 ′ y_1^′ y1′ 是负数,所以 x 2 = x 1 − ∆ 2 = x 1 − ∆ ∗ y 1 ′ x_2=x_1−∆_2=x_1−∆∗y_1^′ x2=x1−∆2=x1−∆∗y1′
……
综上,可得
x m + 1 = x m − ∆ ∗ y m ′ x_{m+1}=x_m−∆∗y_m^′ xm+1=xm−∆∗ym′
即:
x k + 1 = x k − α f ′ ( x k ) x_{k+1}=x_k−α f^′ {(x_k)} xk+1=xk−αf′(xk)
通过上面的迭代一定能找到目标点。
上面说的是一维,如果是多维,比如二维呢?其实是一样的,举个例子:
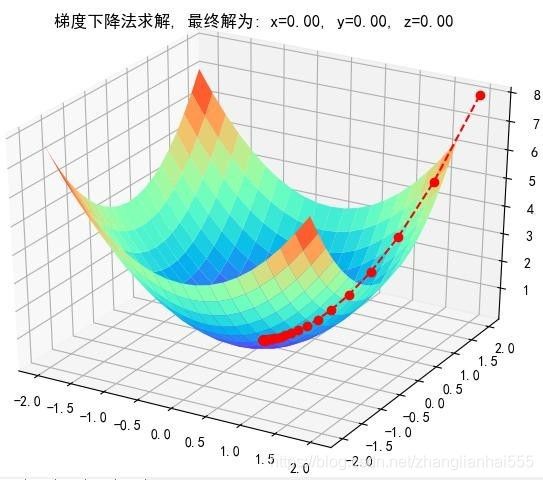
公式推导
基于之前线性回归的目标函数
J ( θ ) = 1 2 ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J{(\theta)} = \frac{1}{2} \sum_{i=1}^m \left( h_\theta \left(x^{(i)} \right) -y^{(i)} \right)^2 J(θ)=21i=1∑m(hθ(x(i))−y(i))2
初始化θ(随机初始化,可以初始为0),沿着负梯度方向迭代,更新后的θ使J(θ)更小(因为J(θ)是一个凸函数,和y=x²类似。如果不是凸函数呢?可能会找到局部最优,而非全局最优。这种情况可采用Adam算法,深度学习中有用到)
θ = θ − α ∙ ∂ J ( θ ) ∂ θ \theta = \theta - \alpha \bullet \frac{\partial J{(\theta)}}{\partial \theta} θ=θ−α∙∂θ∂J(θ)
注 α:学习率、步长,大于0,一般取0.001,0.01,0.1,从小到大调参
总的来说就是沿负梯度方向进行迭代更新
公式推导
J ( θ ) = 1 2 ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J{(\theta)} = \frac{1}{2} \sum_{i=1}^m \left( h_\theta \left(x^{(i)} \right) -y^{(i)} \right)^2 J(θ)=21i=1∑m(hθ(x(i))−y(i))2
右式是累加的形式,可以以其中一项为例,即一个样本
∂ ∂ θ j J ( θ ) = ∂ ∂ θ j 1 2 ( h θ ( x ) − y ) 2 = 2 ⋅ 1 2 ( h θ ( x ) − y ) ⋅ ∂ ∂ θ j ( h θ ( x ) − y ) = ( h θ ( x ) − y ) ⋅ ∂ ∂ θ j ( ∑ i = 1 n θ i x i − y ) = ( h θ ( x ) − y ) x j \begin{aligned} \frac{\partial }{\partial \theta_j} J{(\theta)} &= \frac{\partial }{\partial \theta_j} \frac{1}{2} \left(h_\theta(x)-y \right) ^2 \\ &=2 \cdot \frac{1}{2} \left(h_\theta(x)-y \right) \cdot \frac{\partial }{\partial \theta_j} \left(h_\theta(x)-y \right) \\ &= \left(h_\theta(x)-y \right) \cdot \frac{\partial }{\partial \theta_j} \left( \sum_{i=1}^n \theta_i x_i -y \right) \\ &= \left(h_\theta(x)-y \right) x_j \end{aligned} ∂θj∂J(θ)=∂θj∂21(hθ(x)−y)2=2⋅21(hθ(x)−y)⋅∂θj∂(hθ(x)−y)=(hθ(x)−y)⋅∂θj∂(i=1∑nθixi−y)=(hθ(x)−y)xj
再来看一下
θ = θ − α ∙ ∂ J ( θ ) ∂ θ \theta = \theta - \alpha \bullet \frac{\partial J{(\theta)}}{\partial \theta} θ=θ−α∙∂θ∂J(θ)
这是一个向量的减法,具体的计算,是向量的每一维度进行相应的减操作,因此可以通过循环操作,对每一维度进行更新。
3种梯度下降
1)批量梯度下降算法(BGD)
∂ J ( θ ) ∂ θ j = ( h θ ( x ) − y ) x j \frac{\partial J{(\theta)}}{\partial \theta_j} = \left(h_\theta(x)-y \right) x_j ∂θj∂J(θ)=(hθ(x)−y)xj
∂ J ( θ ) ∂ θ j = ∑ i = 1 m ∂ J ( θ ) ∂ θ j = ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \frac{\partial J{(\theta)}}{\partial \theta_j} = \sum_{i=1}^m \frac{\partial J{(\theta)}}{\partial \theta_j} = \sum_{i=1}^m \left(h_\theta(x^{(i)})-y^{(i)} \right) x_j^{(i)} ∂θj∂J(θ)=i=1∑m∂θj∂J(θ)=i=1∑m(hθ(x(i))−y(i))xj(i)
第一行表示一条数据的情况,如果对于m条数据,就是第二行的累加情况。
批量梯度下降,也就是对 θ j θ_j θj 进行更新时,一次对m条数据进行操作:m条数据导数累加的和,然后再做更新
θ j = θ j + α ∑ i = 1 m ( y ( i ) − h θ ( x ( i ) ) ) x j ( i ) \theta_j = \theta_j + \alpha \sum_{i=1}^m \left(y^{(i)} - h_\theta(x^{(i)}) \right) x_j^{(i)} θj=θj+αi=1∑m(y(i)−hθ(x(i)))xj(i)
2)随机梯度下降算法(SGD)
既然能一次性更新所有的样本,那能不能一次只更新一个样本?这就是随机梯度下降:也就是有一条样本就更新一次 θ j θ_j θj
∂ J ( θ ) ∂ θ j = ( h θ ( x ) − y ) x j \frac{\partial J{(\theta)}}{\partial \theta_j} = \left(h_\theta(x)-y \right) x_j ∂θj∂J(θ)=(hθ(x)−y)xj
总体是趋于最优值。但由于是一条样本一更新,当有异常样本时,可能会出现远离的情况。所以总体往往有波动。
比较
- SGD速度比BGD快(迭代次数少)
- SGD在某些情况下(全局存在多个相对最优解/J(θ)不是一个二次),SGD有可能跳出某些小的局部最优解,所以不会比BGD坏
- BGD一定能够得到一个局部最优解(在线性回归模型中一定是得到一个全局最优解),SGD由于随机性的存在可能导致最终结果比BGD的差
注意:优先选择SGD
3)小批量梯度下降法(MBGD)
如果即需要保证算法的训练过程比较快,又需要保证最终参数训练的准确率,而这正是小批量梯度下降法(Mini-batch Gradient Descent,简称MBGD)的初衷。MBGD中不是每拿一个样本就更新一次梯度,而且拿b个样本(b一般为10)的平均梯度作为更新方向。
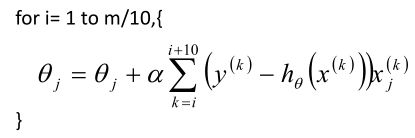
注意点
由于梯度下降法中负梯度方向作为变量的变化方向,所以有可能导致最终求解的值是局部最优解,所以在使用梯度下降的时候,一般需要进行一些调优策略。
学习率的选择:学习率过大,表示每次迭代更新的时候变化比较大,有可能会跳过最优解;学习率过小,表示每次迭代更新的时候变化比较小,就会导致迭代速度过慢,很长时间都不能结束;一般取0.001,0.01,0.1,从小到大调参

算法初始参数值的选择:初始值不同,最终获得的最小值也有可能不同,因为梯度下降法求解的是局部最优解,所以一般情况下,选择多次不同初始值运行算法,并最终返回损失函数最小情况下的结果值;sklearn无此功能
标准化:由于样本不同特征的取值范围不同,可能会导致在各个不同参数上迭代速度不同,为了减少特征取值的影响,可以将特征进行标准化操作。
BGD、SGD、MBGD的区别:
-
当样本量为m的时候,每次迭代BGD算法中对于参数值更新一次,SGD算法中对于参数值更新m次,MBGD算法中对于参数值更新m/n次,相对来讲SGD算法的更新速度最快;
-
SGD算法中对于每个样本都需要更新参数值,当样本值不太正常的时候,就有可能会导致本次的参数更新会产生相反的影响,也就是说SGD算法的结果并不是完全收敛的,而是在收敛结果处波动的;
-
SGD算法是每个样本都更新一次参数值,所以SGD算法特别适合样本数据量大的情况以及在线机器学习(Online ML)。
补充
还经常听到牛顿法(Newton method)和拟牛顿法(quasi Newton method),其实也特别简单,这里只简单介绍一下。
上面说梯度下降法时,得到了式子:
x k + 1 = x k − α f ′ ( x k ) x_{k+1}=x_k−α f^′ {(x_k)} xk+1=xk−αf′(xk)
像牛顿法,其实就是在梯度下降法的基础上做了些变动(α不是超参,而是这一点二阶导的倒数)。
x k + 1 = x k − f ′ ( x k ) f ′ ′ ( x k ) x_{k+1}=x_k−\frac{f^′ {(x_k)}}{f^{''} {(x_k)}} xk+1=xk−f′′(xk)f′(xk)
二阶导就是一阶导的变化率,类似于物理学中的加速度与速度。在用梯度下降迭代优化的过程中,当变动越剧烈的时候,此时,二阶导的值就会越大,而取倒数后,则就会越小,从而能减缓剧烈程度;相反,当迭代优化时,变动比较缓慢,二阶导的倒数就会比较大,此时可以加快迭代。
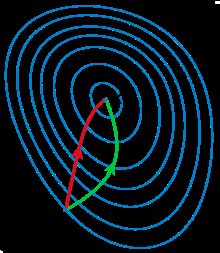
一般认为牛顿法可以利用到曲线本身的信息,比梯度下降法更容易收敛(迭代更少次数),如下图是一个最小化一个目标方程的例子,红色曲线是利用牛顿法迭代求解,绿色曲线是利用梯度下降法求解。
在上面讨论的是低维情况,高维情况的牛顿迭代公式是:
X k + 1 = X k − ( H f ( X k ) ) − 1 ∇ f ( X k ) X_{k+1}=X_k - \left(Hf(X_k) \right) ^{-1} \nabla f(X_k) Xk+1=Xk−(Hf(Xk))−1∇f(Xk)
其中 H H H 就是hessian矩阵(海塞矩阵),他的定义为:
H ( f ) = [ ∂ 2 f ∂ x 1 2 ∂ 2 f ∂ x 1 ∂ x 2 ⋯ ∂ 2 f ∂ x 1 ∂ x n ∂ 2 f ∂ x 2 ∂ x 1 ∂ 2 f ∂ x 2 2 ⋯ ∂ 2 f ∂ x 2 ∂ x n ⋮ ⋮ ⋱ ⋮ ∂ 2 f ∂ x n ∂ x 1 ∂ 2 f ∂ x n ∂ x 2 ⋯ ∂ 2 f ∂ x n 2 ] H(f)= \begin{bmatrix} \frac {\partial^2f}{\partial x_1^2} & \frac {\partial^2f}{\partial x_1 \partial x_2} & \cdots & \frac {\partial^2f}{\partial x_1 \partial x_n} \\ \frac {\partial^2f}{\partial x_2 \partial x_1} & \frac {\partial^2f}{ \partial x_2^2} & \cdots & \frac {\partial^2f}{\partial x_2 \partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac {\partial^2f}{\partial x_n \partial x_1} & \frac {\partial^2f}{\partial x_n \partial x_2} & \cdots & \frac {\partial^2f}{\partial x_n^2} \\ \end{bmatrix} H(f)=⎣⎢⎢⎢⎢⎢⎡∂x12∂2f∂x2∂x1∂2f⋮∂xn∂x1∂2f∂x1∂x2∂2f∂x22∂2f⋮∂xn∂x2∂2f⋯⋯⋱⋯∂x1∂xn∂2f∂x2∂xn∂2f⋮∂xn2∂2f⎦⎥⎥⎥⎥⎥⎤
高维情况依然可以用牛顿迭代求解,牛顿法虽然收敛速度快,但是需要计算海塞矩阵的逆矩阵 H − 1 H^{-1} H−1,计算量会比较大,而且有时目标函数的海塞矩阵无法保持正定(也就是无法求得逆矩阵),从而使得牛顿法失效。为了克服这两个问题,人们提出了拟牛顿法。这个方法的基本思想是:不用二阶偏导数而构造出可以近似海塞矩阵(或海塞矩阵的逆)的正定对称阵。不同的构造方法就产生了不同的拟牛顿法。典型的有DFP算法、BFGS算法、L-BFGS算法等。这里就不再介绍了,感兴趣的可以自己去查相关资料。



