python 通信系统仿真_深入浅出通信原理连载22-40(Python代码版)
深入浅出通信原理Python代码版
深入浅出通信原理是陈爱军的心血之作,于通信人家园连载,此处仅作python代码笔记训练所用
陈老师的连载从多项式乘法讲起,一步一步引出卷积、傅立叶级数展开、旋转向量、三维频谱、IQ调制、数字调制等一系列通信原理知识
连载27 信号调制的意义
无线通信系统是空间辐射的方式传送信号的,而现有天线大都是全向天线,天线尺寸\(l\)大于被辐射波长\(\lambda\)十分之一时方能被有效辐射。通常来说需1/4才能达到较好的接收效果。因此调制后的信号的频率升高波长变短,从而大大降低对天线的需求。
\[\lambda=\frac{c}{f}\\
l>=\frac{1}{10}\lambda
\]
连载24-26: IQ信号调制解调
IQ调制(正交调制)即I路与Q路分别输入两个数据a,b,I路与cos\(w_0\)相乘,Q路与\(-sin\omega_0\)相乘,再将IQ两路叠加,最后获得的信号\(s(t)=acosw_ot-bsinw_0t\)。
通常将输入信号以复数a+bj表示,乘上\(e^{jw_0t}\)再取实部便得到
以下图均引自陈老师通信人家园论坛帖子
连载28 IQ调制称正交调制的原因
IQ信号被调制到了一对正交的载波上。
正弦波与余弦波在一个周期内积分是0
正弦波、余弦波与自身的乘积在一个周期T内积分大于0
\[\frac{2}{T}\int_{-T/2}^{T/2}\cos\omega_0t\sin\omega_0tdt=0 \\
\frac{2}{T}\int_{-T/2}^{T/2}\cos\omega_0t\cos\omega_0tdt
=\frac{2}{T}\int_{-T/2}^{T/2}\left[\frac{1}{2}(1-\cos2\omega_0t)\right]dt
=1
\]
同样,余弦函数集合{\(coswt,2coswt,3coswt,\cdots\)}及正弦函数集合亦具有正交性
任意一个余弦(正弦)函数的平方在基波周期\(T={2\pi}/{\omega_0}\)内积分大于0
任意两个余弦(正弦)函数(不含自身)的乘积在基波周期内积分等于0
正弦函数与余弦函数之间的正交性:
余弦函数集合{\(coswt,2coswt,3coswt,\cdots\)}任一函数与正弦函数集合{\(\sin\omega_0,2sinw_0,3sinw_0,\cdots\)}任一函数的乘积在基波周期内积分为0
\[\frac{2}{T}\int_{-T/2}^{T/2}\cos m\omega_0t\cos m\omega_0tdt
=\frac{2}{T}\int_{-T/2}^{T/2}\left[\frac{1}{2}(1-\cos2m\omega_0t)\right]dt
=1\\
\frac{2}{T}\int_{-T/2}^{T/2}\sin m\omega_0t\sin m\omega_0tdt
=\frac{2}{T}\int_{-T/2}^{T/2}\left[\frac{1}{2}(1-\sin2m\omega_0t)\right]dt
=1\\
\int_{-T/2}^{T/2}\cos m\omega_0t \cos n\omega_0tdt=0 \quad (m!=n)\\
\int_{-T/2}^{T/2}\sin m\omega_0t \sin n\omega_0tdt=0\\
\int_{-T/2}^{T/2}\cos m\omega_0t \sin n\omega_0tdt=0
\]
连载30 OFDM框图
该图n个子载波,承载2n个bit
\[\begin{bmatrix}
{a_{11}}&{a_{12}}&{\cdots}&{a_{1n}}\\
{a_{21}}&{a_{22}}&{\cdots}&{a_{2n}}\\
{\vdots}&{\vdots}&{\ddots}&{\vdots}\\
{a_{m1}}&{a_{m2}}&{\cdots}&{a_{mn}}\\
\end{bmatrix}
\]
连载22-23 CDMA
Walsh Code:
\[W^+=
\begin{bmatrix}
+1 \quad +1 \quad +1 \quad +1\\
+1 \quad-1 \quad +1 \quad-1\\
+1 \quad+1\quad-1\quad -1\\
+1\quad-1\quad-1 \quad+1
\end{bmatrix}
\]
不同行的WAlsh码相乘,再在一个周期T内积分,结果是0
同行Walsh码相乘再在一个周期内积分所得结果是T
CDMA编解码过程:
CDMA中要借助导频(实质上就是m序列)来实现同步,确保walsh码能够对齐,walsh码间保持正交关系。
连载34 PSK调制
PSK(Phase Shift Keying)通过不同载波相位来表征不同比特
BPSK:所得信号 \(\cos\omega t\) 对应比特0,\(\cos(\omega t+\pi)\)对应比特1
QPSK:用4个相位表示00,01,10,11
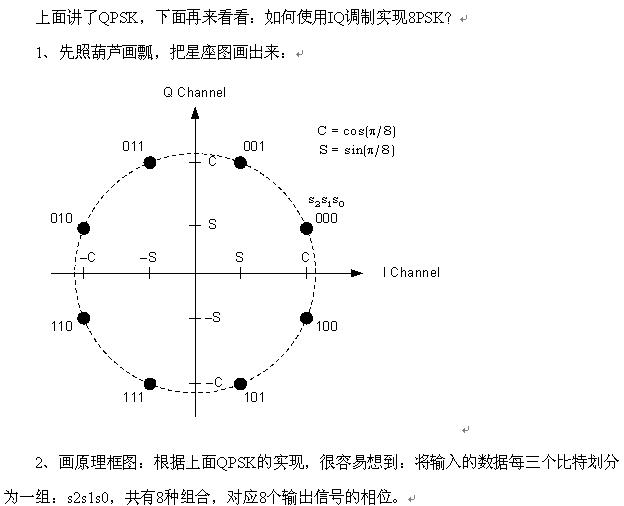
8PSK: 输入001输出\(\cos(wt+\pi/8)\),8个相位表示三个比特
采用IQ调制实现QPSK:
QPSK对应星座图:
折叠代码块
```python
# 连载36:QPSK time doamin waveform
t = np.arange(0,8.5,0.5)
# input
plt.subplot(4,1,1)
y1 = [0,1,1,0,1,1,0,0,0,1,1,0,1,1,0,0,0]
plt.plot(t,y1,drawstyle='steps-post')
plt.xlim(0,8)
plt.ylim(-0.5,1.5)
plt.title('Input Signal')
I Signal
plt.subplot(4,1,2)
a = 1/np.sqrt(2)
tI = np.arange(0,9,1)
yI = [-a,a,-a,a,-a,a,-a,a,a]
plt.plot(tI,yI,drawstyle='steps-post')
plt.xlim(0,8)
plt.ylim(-2,2)
plt.title('I signal')
Q signal
plt.subplot(4,1,3)
yQ = [a,-a,-a,a,a,-a,-a,a,a]
plt.plot(tI,yQ,drawstyle='steps-post')
plt.xlim(0,8)
plt.ylim(-1,1)
plt.title('Q Signal')
QPSK signal
plt.subplot(4,1,4)
t = np.arange(0,9.,0.01)
def outputwave(I,Q,t):
rectwav = []
for i in range(len(I)):
t_tmp = t[((i)100)(i+1)100)]
yI_tmp = yI[i]np.ones(100)
yQ_tmp = yQ[i]np.ones(100)
wav_tmp = yI_tmpnp.cos(2np.pi5t_tmp)-yQ_tmpnp.sin(2np.pi5t_tmp)
rectwav.append(wav_tmp)
return rectwav
rectwav = outputwave(yI,yQ,t)
plt.plot(t,np.array(rectwav).flatten())
plt.xlim(0,8)
plt.ylim(-2,2)
plt.title('QPSK Signal')
plt.tight_layout()
plt.show()

> QPSK的映射关系由格雷码决定,即减小误比特率
| 十进制数 | 自然二进制数 | 格雷码 |
| -------- | ------------ | ------ |
| 0 | 000 | 000 |
| 1 | 001 | 001 |
| 2 | 010 | 011 |
| 3 | 011 | 010 |
| 4 | 100 | 110 |
| 5 | 101 | 111 |
| 6 | 110 | 101 |
| 7 | 111 | 100 |
## 连载39: 8PSK
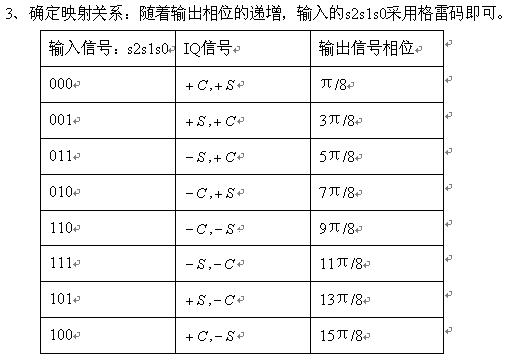
## 连载40: 16QAM

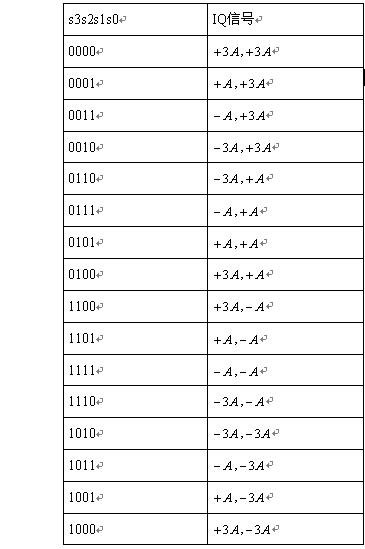
> 前面讲的PSK调制(QPSK、8PSK),星座图中的点都位于单位圆上,模相同(都为1),只有相位不同。而QAM调制星座图中的点不再位于单位圆上,而是分布在复平面的一定范围内,各点如果模相同,则相位必不相同,如果相位相同则模必不相同。星座图中点的分布是有讲究的,不同的分布和映射关系对应的调制方案的误码性能是不一样的
由于部分图片显示不出,故贴上[Github地址](https://github.com/weidongz/Rubbish_Code/blob/master/Understanding_Communication_Theroy/Blog_22-40.md)备用