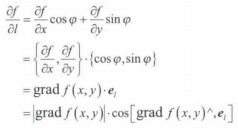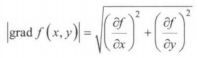人工智能之数学基础篇—高等数学基础(下篇)
人工智能之数学基础篇—高等数学基础(下篇)
- 6 方向导数
-
- 6.1 方向导数的定义
- 6.2 方向导数的几何意义
- 7 梯度
- 8 综合实例一梯度下降法求函数的最小值
- 9 Python中相关库简介
-
- 9.1 SymPy库简介
- 9.2 NumPy库简介
- 9.3 SciPy库简介
- 9.4 求导的3种方式
最后,来重点介绍一下方向导数和梯度。因为梯度下降法是机器学习领域非常重要的算法之一,也是应用广泛的优化算法之一。在本篇文章中,我将综合实例来重点介绍梯度下降法及其应用,并利用Python语言编程实现。查看本文之前,可以先阅读人工智能之数学基础篇—高等数学基础上篇和人工智能之数学基础篇—高等数学基础中篇。
6 方向导数
6.1 方向导数的定义
由二元函数偏导数的概念,我们知道函数 f ( x , y ) f(x,y) f(x,y) 在点 ( x 0 , y 0 ) \left ( x_{0},y_{0} \right ) (x0,y0) 处的两个偏导数,分别是函数 f f f 在点 ( x 0 , y 0 ) \left ( x_{0},y_{0} \right ) (x0,y0) 处沿与 x x x 轴和 y y y 轴平行的方向的变化率。但是在许多实际问题中,仅仅研究函数沿这两个特殊方向的变化率是远远不够的,还需要研究函数沿各个不同方向的变化率。例如,在大气气象中,就需要研究温度、气压沿不同方向的变化率。这就是所谓的方向导数。
从上述的分析中可以看出,偏导数反映的是函数沿坐标轴方向的变化率,方向导数本质上研究的是函数在某点处沿某特定方向的变化率问题。
比如 z = f ( x , y ) z=f(x,y) z=f(x,y) 在点 p ( x 0 , y 0 ) p\left ( x_{0},y_{0} \right ) p(x0,y0) 沿方向 l l l 的变化率。假设方向如图10所示, l l l 为 x O y xOy xOy 平面上以 p p p 为起始点的一条射线, p ′ p^{'} p′ 为方向 l l l 上的另一点。
由图10可知, p p p 与 p ′ p^{'} p′之间的距离 ∣ p p ′ ∣ = ρ = Δ x 2 + Δ y 2 \left | pp^{'} \right | = \rho = \sqrt{\Delta x^{2} + \Delta y^{2}} ∣∣∣pp′∣∣∣=ρ=Δx2+Δy2。
函数的增量 Δ z = f ( x 0 + Δ x , y 0 + Δ y ) − f ( x 0 , y 0 ) \Delta z = f\left ( x_{0}+\Delta x, y_{0}+\Delta y \right ) - f\left ( x_{0},y_{0} \right ) Δz=f(x0+Δx,y0+Δy)−f(x0,y0)。
考虑函数的增量与这两点间距离的比值,当 p ′ p^{'} p′ 沿着方向 l l l 趋于 p p p 时,如果这个比的极限存在,则称这个极限为函数 f ( x , y ) f(x,y) f(x,y) 在点 p p p 沿方向 l l l 的方向导数,记作 ∂ f ∂ l \frac{\partial f}{\partial l} ∂l∂f,即
∂ f ∂ l = lim ρ → 0 f ( x 0 + Δ x , y 0 + Δ y ) − f ( x 0 , y 0 ) ρ \frac{\partial f}{\partial l}= \lim_{\rho \rightarrow 0}\frac{f\left ( x_{0}+\Delta x, y_{0}+\Delta y \right ) - f\left ( x_{0},y_{0} \right )}{\rho } ∂l∂f=ρ→0limρf(x0+Δx,y0+Δy)−f(x0,y0)
从定义可知,当函数 f ( x , y ) f(x,y) f(x,y) 在点 p ( x 0 , y 0 ) p\left ( x_{0},y_{0} \right ) p(x0,y0) 的偏导数 f x ( x 0 , y 0 ) f_{x}\left ( x_{0},y_{0} \right ) fx(x0,y0)、 f y ( x 0 , y 0 ) f_{y}\left ( x_{0},y_{0} \right ) fy(x0,y0) 存在时,函数 f ( x , y ) f(x,y) f(x,y) 在 p p p 点沿着 x x x 轴正向单位向量 e 1 = { 1 , 0 } e_{1}=\left \{ 1,0 \right \} e1={ 1,0}, y y y 轴正向单位向量 e 2 = { 0 , 1 } e_{2}=\left \{ 0,1 \right \} e2={ 0,1} 的方向导数存在,且其值依次为 f x ( x 0 , y 0 ) f_{x}\left ( x_{0},y_{0} \right ) fx(x0,y0), f y ( x 0 , y 0 ) f_{y}\left ( x_{0},y_{0} \right ) fy(x0,y0);函数 f ( x , y ) f(x,y) f(x,y) 在 p p p 点沿着 x x x 轴负向单位向量 e 1 ′ = { − 1 , 0 } e_{1}^{'}=\left \{ -1,0 \right \} e1′={ −1,0}, y y y 轴负向单位向量 e 2 ′ = { 0 , − 1 } e_{2}^{'}=\left \{ 0,-1 \right \} e2′={ 0,−1} 的方向导数存在,且其值依次为 − f x ( x 0 , y 0 ) -f_{x}\left ( x_{0},y_{0} \right ) −fx(x0,y0), − f y ( x 0 , y 0 ) -f_{y}\left ( x_{0},y_{0} \right ) −fy(x0,y0)。
方向导数 ∂ f ∂ l \frac{\partial f}{\partial l} ∂l∂f 的存在及计算如下定理。
定理5 如果函数 z = f ( x , y ) z=f(x,y) z=f(x,y) 在点 p ( x 0 , y 0 ) p\left ( x_{0},y_{0} \right ) p(x0,y0) 是可微分的,那么函数在该点沿任意方向 l l l 的方向导数都存在,且有
∂ f ∂ l = ∂ f ∂ x c o s φ + ∂ f ∂ y s i n φ \frac{\partial f}{\partial l}=\frac{\partial f}{\partial x}cos\varphi +\frac{\partial f}{\partial y}sin\varphi ∂l∂f=∂x∂fcosφ+∂y∂fsinφ
其中 φ \varphi φ 为 x x x 轴到 l l l 方向的转角。
6.2 方向导数的几何意义
方向导数的几何意义如图11所示,函数 z = f ( x , y ) z=f(x,y) z=f(x,y) 的变化方向为 l l l,方向导数 ∂ f ∂ l ∣ p \left.\begin{matrix} \frac{\partial f}{\partial l} \end{matrix}\right|_{p} ∂l∂f∣∣p 是函数 z = f ( x , y ) z=f(x,y) z=f(x,y) 在点 p p p 处沿方向 l l l 的变化率,从方向 l l l 作垂直于 x O y xOy xOy 平面的一个平面,与曲面相交成一条曲线 M Q MQ MQ, ∂ f ∂ l ∣ p \left.\begin{matrix} \frac{\partial f}{\partial l} \end{matrix}\right|_{p} ∂l∂f∣∣p 即为曲线 M Q MQ MQ 在 M M M 点的切线 M N MN MN 的斜率。
【例13】求函数 z = x e 2 y z = xe^{2y} z=xe2y 在点 P ( 1 , 0 ) P\left ( 1,0 \right ) P(1,0) 到点 Q ( 2 , − 1 ) Q\left ( 2,-1 \right ) Q(2,−1) 方向的方向导数。
解:这里方向 l l l 即向量 P Q → = { 1 , − 1 } \overrightarrow{PQ}=\left \{ 1,-1 \right \} PQ={ 1,−1} 的方向,因此 x x x 轴到方向 l l l 的转角 φ = − π 4 \varphi = -\frac{\pi }{4} φ=−4π,

由方向导数的意义可知,方向导数 ∂ f ∂ l ∣ p \left.\begin{matrix} \frac{\partial f}{\partial l} \end{matrix}\right|_{p} ∂l∂f∣∣p 是 z = f ( x , y ) z=f(x,y) z=f(x,y) 在点 p p p 处沿方向 l l l 的变化率,是曲面上过 M M M 点的一条曲线的切线的斜率,那么点 p p p 在某一方向的变化率,就是过曲面 M M M 点的某一条曲线的切线的斜率。根据曲面的切平面与法线的相关概念可知,曲面上通过点 M M M 且在点 M M M 处具有切线的曲线,它们在点 M M M 处的切线都在同一个平面上,这个平面称为切平面。因此方向导数 ∂ f ∂ l ∣ p \left.\begin{matrix} \frac{\partial f}{\partial l} \end{matrix}\right|_{p} ∂l∂f∣∣p 为过 M M M 点的切平面上的某条直线的斜率,那么哪一个方向的变化率最大呢?下面继续讨论。
7 梯度
定义16 设函数 z = f ( x , y ) z=f(x,y) z=f(x,y) 在平面区域 D D D 内具有一阶连续偏导数,则对于每一点 p ( x , y ) ϵ D p\left ( x,y \right )\epsilon D p(x,y)ϵD,都可定出一个向量 ∂ f ∂ x i → + ∂ f ∂ y j → \frac{\partial f}{\partial x}\overrightarrow{i}+\frac{\partial f}{\partial y}\overrightarrow{j} ∂x∂fi+∂y∂fj,这个向量称为函数 z = f ( x , y ) z=f(x,y) z=f(x,y) 在点 p ( x , y ) p(x,y) p(x,y) 的梯度,记作 g r a d f ( x , y ) gradf(x,y) gradf(x,y),即
g r a d f ( x , y ) = ∂ f ∂ x i → + ∂ f ∂ y j → gradf(x,y) = \frac{\partial f}{\partial x}\overrightarrow{i}+\frac{\partial f}{\partial y}\overrightarrow{j} gradf(x,y)=∂x∂fi+∂y∂fj
设 e l → = c o s φ i → + s i n φ j → \overrightarrow{e_{l}} = cos\varphi\overrightarrow{i}+sin\varphi \overrightarrow{j} el=cosφi+sinφj 是与方向 l l l 同方向的单位向量(其中 φ \varphi φ 为 x x x 轴到方向 l l l 的转角),则由方向导数的计算公式可知:
![]()
由公式推导可以看出,方向导数 ∂ f ∂ l \frac{\partial f}{\partial l} ∂l∂f 等于梯度与 e l → \overrightarrow{e_{l}} el 的乘积,即梯度的模 ∣ g r a d f ( x , y ) ∣ \left | grad\, f\left ( x,y \right ) \right | ∣gradf(x,y)∣ 在方向 l l l 上的投影,当方向 l l l 与梯度的方向一致时,方向导数 ∂ f ∂ l \frac{\partial f}{\partial l} ∂l∂f 有最大值。所以,沿梯度方向的方向导数达到最大值,也就是说,梯度方向是函数 z = f ( x , y ) z=f(x,y) z=f(x,y) 在这点增长最快的方向。因此,可以得到如下结论。
函数在某点的梯度是一个向量,它的方向与取得最大方向导数的方向一致,而它的模为方向导数的最大值。
一般来说,函数 z = f ( x , y ) z=f(x,y) z=f(x,y) 在几何上表示一个曲面,这个曲面被平面 z = c z=c z=c ( c c c 是常数)所截得的曲线 l l l 的方程为:
{ z = f ( x , y ) z = c \begin{cases} z = f(x,y) & \\ z = c & \end{cases} { z=f(x,y)z=c
这条曲线 l l l 在 x O y xOy xOy 平面上的投影是平面曲线 L ∗ L^{*} L∗,它在 x O y xOy xOy 平面直角坐标系中的方程为 f ( x , y ) = c f(x,y)=c f(x,y)=c。曲线 L ∗ L^{*} L∗ 上的任意点,函数值都是 c c c,所以称平面曲线 L ∗ L^{*} L∗ 为函数 z = f ( x , y ) z=f(x,y) z=f(x,y) 的等高线。
由于等高线 f ( x , y ) = c f(x,y)=c f(x,y)=c 上任意点 ( x , y ) (x,y) (x,y) 处的法线的斜率为:
− 1 d y d x = − 1 ( − f x f y ) = f y f x -\frac{1}{\frac{dy}{dx}}=-\frac{1}{\left ( -\frac{f_{x}}{f_{y}} \right )}=\frac{f_{y}}{f_{x}} −dxdy1=−(−fyfx)1=fxfy
所以梯度
g r a d f ( x , y ) = ∂ f ∂ x i → + ∂ f ∂ y j → gradf(x,y) = \frac{\partial f}{\partial x}\overrightarrow{i}+\frac{\partial f}{\partial y}\overrightarrow{j} gradf(x,y)=∂x∂fi+∂y∂fj为等高线上点 ( x , y ) (x,y) (x,y) 处的法向量,因此可得到梯度与等高线的关系如下。
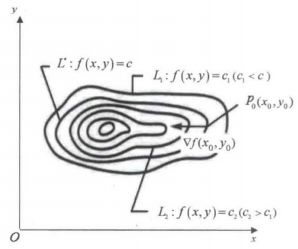
如图12所示,图中显示了6条等高线,在等高线 f ( x , y ) = c f(x,y)=c f(x,y)=c 上有一点 p 0 ( x 0 , y 0 ) p_{0}\left ( x_{0},y_{0} \right ) p0(x0,y0),可以看出点 p 0 ( x 0 , y 0 ) p_{0}\left ( x_{0},y_{0} \right ) p0(x0,y0) 的切线与法线垂直。图中 c 2 > c > c 1 c_{2}>c>c_{1} c2>c>c1, p 0 ( x 0 , y 0 ) p_{0}\left ( x_{0},y_{0} \right ) p0(x0,y0) 点的法线方向与梯度 ▽ f ( x 0 , y 0 ) \triangledown f\left ( x_{0},y_{0} \right ) ▽f(x0,y0) 相同。
梯度为方向导数取最大值的方向的概念并不好理解。再通俗一点,设想曲面为一座高山,而这座山像一个球的半面,如图13所示。现在,有一个人站在半山腰 p p p 点位置上,他想要寻找下山最快的方向,在他所处的位置做一个切面,所有的方向导数都在此切面上,哪一个方向使他下山最快呢?采用他所处位置的等高线的切线的法向量最快,由于是下山,因此采用的是梯度的反方向。

【例14】求函数 u = x y z + z 2 + 5 u=xyz+z^{2}+5 u=xyz+z2+5,求 g r a d u grad\, u gradu 及在点 M ( 0 , 1 , − 1 ) M(0,1,-1) M(0,1,−1) 处方向导数的最大值。
8 综合实例一梯度下降法求函数的最小值
梯度下降法,是寻找函数极小值最常用的优化方法。当目标函数是凸函数时,梯度下降法的解是全局解。但在一般情况下,其解不保证是全局最优解。最普遍的做法是,在已知参数当前值时,按当前点对应的梯度向量的反方向及事先定好的步长大小对参数进行调整。按上述方法对参数做出多次调整之后,函数就会通近一个极小值。
例如,假设函数 f ( x ) f(x) f(x) 为一元连续函数,初始值为 x 0 x_{0} x0, α \alpha α 为步长,已知在点 x 0 x_{0} x0 的梯度为 g r a d f ( x 0 ) grad\, f\left ( x_{0} \right ) gradf(x0),那么下一个点的坐标为 x 1 = x 0 − α ∗ g r a d f ( x 0 ) x_{1}=x_{0}-\alpha *grad\, f\left ( x_{0} \right ) x1=x0−α∗gradf(x0),然后再求点 x 1 x_{1} x1 的梯度,反复迭代,直到 f ( x n ) − f ( x n − 1 ) f\left ( x_{n} \right )-f\left ( x_{n-1} \right ) f(xn)−f(xn−1) 的绝对差极小,迭代结束,此时的 f ( x n ) f\left ( x_{n} \right ) f(xn) 即为极小值。
下面举一个例子来说明梯度下降法的基本原理。
假设曲面上一只蚂蚁突遇火灾,该如何快速逃跑呢?此问题可以类比为一个下山的过程:假设蚂蚁被困在高山上,需要快速找到山的最低点,即山谷。但此时山上的烟雾很大,可视度很低,下山的路径无法确定,它必须利用自己周围的信息去寻找。这个时候,它就可以利用梯度下降法来帮助自己下山。以它当前所处的位置为基准,寻找这个位置最陡峭的地方,朝着山的高度下降最快的地方走。但是,由于山的地形复杂,坡度变化随机,这样一直往下走无法确定路径是否正确,因此可以采用每走一段距离,都反复采用同一个方法(即寻找当前位置最陡峭的地方,朝着山的高度下降最快的地方走),最后就能成功地抵达山谷。
梯度下降的过程就与蚂蚁下山的场景类似。
首先,有一个可微分的函数 f ( x ) f(x) f(x),这个函数就代表着一座山,我们的目标就是找到这个函数的最小值,也就是山底。根据之前的场景假设,最快下山的方式就是找到当前位置最陡峭的方向,然后沿着此方向向下走,对应到函数中,就是找到给定点 x 0 ϵ I x_{0}\, \epsilon \, I x0ϵI 的梯度,梯度相反的方向就能让函数值下降最快。重复利用这个方法,反复求取梯度,最后就能到达局部的最小值。梯度下降法搜索迭代过程如图14所示。

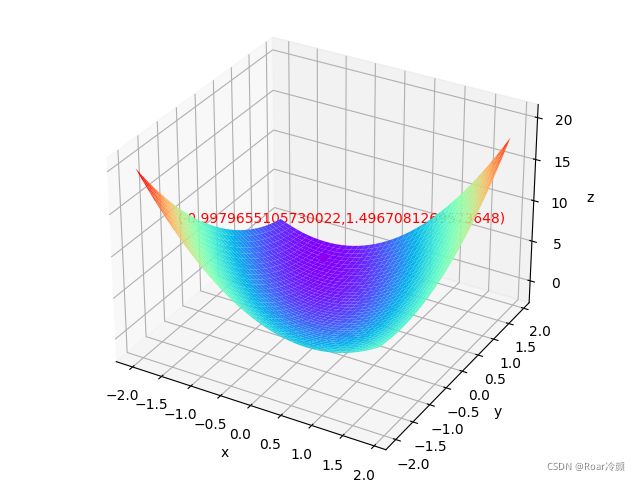
【例15】应用 P y t h o n Python Python 编程实现梯度下降法求解下面函数的最小值,并使用 M a t p l o t l i b Matplotlib Matplotlib、 m p l − t o o l k i t s mpl_{-}toolkits mpl−toolkits 库画出函数的图形。
m i n f ( x ) = x 1 − x 2 + 2 x 1 2 + 2 x 1 x 2 + x 2 2 min\, f\left ( x \right ) = x_{1}-x_{2}+2x_{1}^{2}+2x_{1}x_{2}+x_{2}^{2} minf(x)=x1−x2+2x12+2x1x2+x22给定初值 X ( 0 ) = ( 0 , 0 ) T X^{\left ( 0 \right )}=\left ( 0,0 \right )^{T} X(0)=(0,0)T。
解: m a t p l o t l i b . p y p l o t matplotlib.pyplot matplotlib.pyplot 是一个有命令风格的函数集合,它看起来和 M A T L A B MATLAB MATLAB 很相似,每一个 p y p l o t pyplot pyplot 函数都使一幅图像 f i g u r e figure figure 做出些许改变; m p l − t o o l k i t s . m p l o t 3 d mpl_{-}toolkits.mplot3d mpl−toolkits.mplot3d 是三维工具包。本例中 m p l o t 3 d mplot3d mplot3d 仍使用 f i g u r e figure figure 对象,只不过 A x e s Axes Axes 对象要替换为该工具集的 A x e s 3 d Axes3d Axes3d 对象。
【代码如下】
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d.axes3d import Axes3D
# f(w1,w2) = w1 - w2 + 2*w1^2 + w2^2 + 2*w1*w2
def target_function(w): # 目标函数
w_1, w_2 = w
return w_1 - w_2 + 2 * w_1 ** 2 + w_2 ** 2 + 2 * w_1 * w_2
def gradient_function(w): # 梯度函数:分别对w1,w2求偏导
w_1, w_2 = w
w1_grad = 1 + 4 * w_1 + 2 * w_2
w2_grad = -1 + 2 * w_1 + 2 * w_2
return np.array([w1_grad, w2_grad])
# 梯度下降算法
def batch_gradient_distance(target_func, gradient_func, init_w, learning_rate=0.0008, tolerance=7e-9):
w = init_w
target_value = target_func(w)
counts = 0 # 用于计算次数
while counts < 50000:
gradient = gradient_func(w)
next_w = w - gradient * learning_rate
next_target_value = target_func(next_w)
if abs(next_target_value-target_value) < tolerance:
print("此结果经过了", counts, "次循环")
return next_w
else:
w, target_value = next_w, next_target_value
counts += 1
else:
print("没有取到极值点")
if __name__ == '__main__':
init_w = np.array([0, 0]) # 初始坐标点为(0,0)
w1, w2 = batch_gradient_distance(target_function, gradient_function, init_w)
print(w1, w2)
# 画图
x1 = np.arange(-2, 2, 0.1)
x2 = np.arange(-2, 2, 0.1)
x1, x2 = np.meshgrid(x1, x2) # meshgrid :3D坐标系
z = x1 - x2 + 2 * x1 ** 2 + x2 ** 2 + 2 * x1 * x2
fig = plt.figure() # figure 对象
ax = Axes3D(fig, auto_add_to_figure=False) # Axes3D 对象
fig.add_axes(ax)
# fig = plt.figure()
# ax = fig.gca(projection='3d')
ax.plot_surface(x1, x2, z, rstride=1, cstride=1, cmap="rainbow") # 绘制3D坐标系中的函数图像
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.scatter(w1, w2, target_function([w1, w2]), s=30, c='red') # 绘制已经找到的极值点
ax.text(-2, -1, 10, '(' + str(w1) + "," + str(w2) + ')', color='red')
plt.show()
9 Python中相关库简介
在高等数学基础篇的三篇文章中利用了Python来求解相关的问题,主要用到了SymPy 、 NumPy 、 SciPy 、 Matplotlib 库 。因此,接下来将对几个相关的库做简要总结。
9.1 SymPy库简介
SymPy 是 Python 的一个科学计算库,用强大的符号计算体系完成诸如多项式求值、求极限 、求导 、解方程 、求积分 、解微分方程、级数展开 、矩阵运算等计算 。
(1)常用的 SymPy 内置符号
自然对数的底 e e e 的表示方式 。
【代码如下】
import sympy
print(sympy.E)
print(sympy.log(sympy.E)) # 自然对数的底 e 的表示方式。
E
1
无穷大 ∞ \infty ∞ 的表示方式 。
【代码如下】
import sympy
print(1/sympy.oo) # 无穷大 ∞ 的表示方式。
0
圆周率 π π π 的表示方式 。
【代码如下】
import sympy
print(sympy.sin(sympy.pi)) # 圆周率 π 的表示方式。
0
(2)用 SymPy 进行初等运算
常用的函数有:求对数函数 sympy.log 、正弦函数 sympy.sin 、求平方根函数 sympy.sqrt 、求 n 次方根函数 sympy.root、求阶乘函数 sympy.factorial 等。
(3)表达式与表达式求值
SymPy 可以用一套符号系统来表示一个表达式,如函数、多项式等,并且可以进行求值。
【代码如下】
import sympy
x = sympy.Symbol('x')
fx = 2*x + 1 # fx 是一个表达式
print(fx.evalf(subs={
x: 2})) # 用 evalf() 函数,传入变量的值,对表达式进行求值
x, y = sympy.symbols('x y')
f = 2 * x + y
f.evalf(subs={
x: 1, y: 2}) # 以字典的形式传入多个变量的值
print(f.evalf(subs={
x: 1})) # 如果只传入一个变量的值,则输出原来的表达式
print(f.evalf(subs={
x: 1, y: 2})) # 用 evalf() 函数,传入变量的值,对表达式进行求值
5.00000000000000
y + 2.0
4.00000000000000
(4)利用 SymPy 求极限
使用函数 sympy.limit 求极限,可以参考人工智能之数学基础篇—高等数学基础(上篇)中的例5、例6和例8。
(5)利用 SymPy 求导
使用函数 sympy.diff 求导数,传入两个参数即函数表达式和变量名,可以参考人工智能之数学基础篇—高等数学基础(中篇)中的例10和例11。
9.2 NumPy库简介
NumPy 是 Python 的一个扩展程序库,支将大维度数组与矩阵运算,此外也针对数组运算提供大量的数学函数库。NumPy 是一个运行速度非常快的数学库,主要用于数组计算。
NumPy 通常与 SciPy 和 Matplotlib (绘图库)一起使用, 这种组合广泛应用于替代MATLAB,是一个强大的科学计算环境。 在本篇文章例15中就利用了这些库实现了求函数最小值的解,并用 NumPy 和 Matplotlib 的一些函数实现了函数图像的可视化。
(1)数组的操作
【代码如下】
import numpy as np
a = np.array([1, 2, 3]) # 创建一个秩 (rank)1 数组
print(a[0], a[1], a[2])
b = np.array([[1, 2, 3], [4, 5, 6]]) # 创建一个秩 2 数组
print(b[0, 0], b[0, 1], b[1, 0])
1 2 3
1 2 4
(2)在绘制三维图表时,需要用到 NumPy 中的 mgrid 函数。它会返回一个密集的多维网格,一般形式为 np.mgrid[start: end: step],其中 start 表示开始值,end 表示结束坐标(不包含此点), step表示步数。
【代码如下】
import numpy as np
print(np.mgrid[-1:4:2])
[-1 1 3]
print(np.mgrid[-1:4:2, -3:1:1])
[[[-1 -1 -1 -1]
[ 1 1 1 1]
[ 3 3 3 3]]
[[-3 -2 -1 0]
[-3 -2 -1 0]
[-3 -2 -1 0]]]
print(np.mgrid[-1:4:2, -3:1:2])
[[[-1 -1]
[ 1 1]
[ 3 3]]
[[-3 -1]
[-3 -1]
[-3 -1]]]
9.3 SciPy库简介
SciPy 是世界上著名的 Python 开源科学计算库,构建在 NumPy 之上,功能更为强大。SciPy 函数库在 NumPy 库的基础上增加了众多的数以及工程计算中常用的库函数。可以说,NumPy 是一个纯数学的计算模块, 而 SciPy 是一个更高阶的科学计算库 。SciPy 库需要 NumPy 库的支持。由于这种依赖关系,NumPy 库的安装要先于 SciPy 库。后面会使用该库来计算函数的积分。
9.4 求导的3种方式
(1)使用 SymPy 的 diff 函数,可以得到 f ( x ) f(x) f(x) 的导数表达式;
(2)使用 scipy.misc 模块下的 derivative 函数。SciPy 的求导相对简单也容易理解。
【代码如下】
import numpy as np
from scipy.misc import derivative
def f(x):
return x**5
print(derivative(f, 2, dx=1e-6)) # 对函数在 x=2 处求导
80.00000000230045
(3)使用 NumPy 模块里 polyld 函数构造 f ( x ) f(x) f(x),polyld 函数的形参是多项式的系数,最左侧的是最高次数的系数,构造的函数为多项式。NumPy 的 polyder 函数和 deriv 函数的作用差不多,都是对多项式求导,可以得到函数导数的表达式和在某点的导数。
【例16】对多项式 x 5 + 2 x 4 + 3 x 2 + 5 x^{5}+2x^{4}+3x^{2}+5 x5+2x4+3x2+5 求导。
【代码如下】
import numpy as np
p = np.poly1d([1, 2, 0, 3, 0, 5]) # 构造多项式
print(p) # 下面两行为多项式的显示形式,5、4、2 是下一行项数所对应的幂次。
5 4 2
1 x + 2 x + 3 x + 5
print(np.polyder(p, 1)) # 求一阶导数
4 3
5 x + 8 x + 6 x
print(np.polyder(p, 1)(1.0)) # 求一阶导数在点 x=1 的值。
19.0
print(p.deriv(1)) # 求一阶导数
4 3
5 x + 8 x + 6 x
print(p.deriv(1)(1.0)) # 求一阶导数在点 x=1 的值。
19.0