第一次作业：深度学习基础

Part1: 深度学习概述：（链接：结论和深度学习概述）

主要介绍了从专家系统到机器学习、从传统机器学习到深度学习的变化历程，以及深度学习的能与不能。一些名词概念的区别简单总结如下：

 1. 专家系统：根据专家人工定义的规则，进行推理判断，解决问题。

           机器学习：机器从数据中提取知识自动训练，解决问题。

2. 监督学习：数据标记已知，目的在于学习输入。

    无监督学习：数据标记未知，目的在于发现数据中模式或有意义的信息。

    半监督学习：部分数据标记已知，是监督学习和无监督学习的混合。

    强化学习：数据标记未知但知道与输出目标相关的反馈，适用决策类问题

3. 深度学习的“不能”与解释性：

稳定性低、可调试性差>>找得到  “对症下药” ，出问题快速准确纠错

参数不透明、机器偏见>>看得懂  不再“对牛弹琴”，算法+人的知识体系

增量型差、推理能力差>>留得下  “站在巨人的肩膀上”，越学越聪明

4. 浅层神经网络：

生物神经元、M-P神经元

万有逼近定理：如果一个隐层包含足够多的神经元，三层前馈神经网络（输入-隐层-输出）能以任意任意精度逼近任意预定的连续函数

Part2: 李沐课程学习：（链接：https://link.zhihu.com/?target=http://courses.d2l.ai/zh-v2/）

 一、代码练习环境 

在谷歌 Colab 上的 Jupyter 笔记本环境完成 pytorch 代码练习，使用方法参考：https://www.cnblogs.com/lfri/p/10471852.html 

二、数据操作

导入 torch

import torch

张量：表示由一个数值组成的数组，这个数组可能有多个维度。具有一个轴的张量对应数学上的向量。具有两个轴的张量对应数学上的矩阵。具有两个轴以上的张量没有特殊的数学名称。

使用arange创建一个行向量x。这个行向量包含从0开始的前12个整数，默认创建为浮点数。张量中的每个值都称为张量的元素。

x = torch.arange(12)

x.shape

#通过张量的shape属性来访问张量的形状 （沿每个轴的长度）。

x.numel()

X = x.reshape(3, 4)

#要改变一个张量的形状而不改变元素数量和元素值，可以调用reshape函数

torch.zeros((2, 3, 4))

torch.ones((2, 3, 4))

torch.randn(3, 4)

torch.tensor([[2, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])

• 深度学习存储和操作数据的主要接口是张量（n维数组）。它提供了各种功能，包括基本数学运算、广播、索引、切片、内存节省和转换其他Python对象。

三、数据预处理

先创建一个人工数据集，并存储在csv（逗号分隔值）文件

import os

os.makedirs(os.path.join('..', 'data'), exist_ok=True)
data_file = os.path.join('..', 'data', 'house_tiny.csv')
with open(data_file, 'w') as f:
    f.write('NumRooms,Alley,Price\n')
    f.write('NA,Pave,127500\n')
    f.write('2,NA,106000\n')
    f.write('4,NA,178100\n')
    f.write('NA,NA,140000\n')

再从创建的csv文件中加载原始数据集

import pandas as pd

data = pd.read_csv(data_file)
print(data)

   NumRooms Alley   Price
0       NaN  Pave  127500
1       2.0   NaN  106000
2       4.0   NaN  178100
3       NaN   NaN  140000

为了处理缺失的数据，典型的方法包括插值和删除， 考虑插值

inputs, outputs = data.iloc[:, 0:2], data.iloc[:, 2]
inputs = inputs.fillna(inputs.mean())
print(inputs)

   NumRooms Alley
0       3.0  Pave
1       2.0   NaN
2       4.0   NaN
3       3.0   NaN

对于inputs中的类别值或离散值，将“NaN”视为一个类别

inputs = pd.get_dummies(inputs, dummy_na=True)
print(inputs)

   NumRooms  Alley_Pave  Alley_nan
0       3.0           1          0
1       2.0           0          1
2       4.0           0          1
3       3.0           0          1

现在inputs和outputs中的所有条目都是数值类型，可以转换为张量格式

import torch

X, y = torch.tensor(inputs.values), torch.tensor(outputs.values)
X, y

(tensor([[3., 1., 0.],
         [2., 0., 1.],
         [4., 0., 1.],
         [3., 0., 1.]], dtype=torch.float64),
 tensor([127500, 106000, 178100, 140000]))

四、线性代数

 一些主要知识点学习和复习：

（一般只用F范数）

pytorch代码实现： 

标量由只有一个元素的张量表示

import torch

x = torch.tensor([3.0])
y = torch.tensor([2.0])

x + y, x * y, x / y, x**y

(tensor([5.]), tensor([6.]), tensor([1.5000]), tensor([9.]))

可将向量视为标量值组成的列表

x = torch.arange(4)
x
tensor([0, 1, 2, 3])

通过张量的索引来访问任一元素

x[3]
tensor(3)

访问张量的长度

len(x)

只有一个轴的张量，形状只有一个元素

x.shape
torch.Size([4])

通过指定两个分量m和n来创建一个形状为m×n的矩阵

A = torch.arange(20).reshape(5, 4)
A
tensor([[ 0,  1,  2,  3],
        [ 4,  5,  6,  7],
        [ 8,  9, 10, 11],
        [12, 13, 14, 15],
        [16, 17, 18, 19]])

矩阵的转置

A.T
tensor([[ 0,  4,  8, 12, 16],
        [ 1,  5,  9, 13, 17],
        [ 2,  6, 10, 14, 18],
        [ 3,  7, 11, 15, 19]])

对称矩阵A等于其转置：A=A⊤

B = torch.tensor([[1, 2, 3], [2, 0, 4], [3, 4, 5]])
B
tensor([[1, 2, 3],
        [2, 0, 4],
       [3, 4, 5]])
B == B.T
tensor([[True, True, True],
        [True, True, True],
        [True, True, True]])

给定具有相同形状的任意两个张量，任何按元素二元运算的结果都将是相同形状的张量

两个矩阵的按元素乘法称为哈达玛积（数学符号⊙）

A * B 
tensor([[  0.,   1.,   4.,   9.],
        [ 16.,  25.,  36.,  49.],
        [ 64.,  81., 100., 121.],
        [144., 169., 196., 225.],
        [256., 289., 324., 361.]])
a = 2
X = torch.arange(24).reshape(2, 3, 4)
a + X, (a * X).shape
(tensor([[[ 2,  3,  4,  5],
          [ 6,  7,  8,  9],
          [10, 11, 12, 13]],
 
         [[14, 15, 16, 17],
          [18, 19, 20, 21],
          [22, 23, 24, 25]]]),
 torch.Size([2, 3, 4]))

计算其元素的和

x = torch.arange(4, dtype=torch.float32)
x, x.sum()
(tensor([0., 1., 2., 3.]), tensor(6.))

表示任意形状张量的元素和

A.shape, A.sum()
(torch.Size([5, 4]), tensor(190.))

指定张量沿哪一个轴来通过求和降低维度

A_sum_axis0 = A.sum(axis=0)
A_sum_axis0, A_sum_axis0.shape
(tensor([40., 45., 50., 55.]), torch.Size([4]))

A_sum_axis1 = A.sum(axis=1)
A_sum_axis1, A_sum_axis1.shape
(tensor([ 6., 22., 38., 54., 70.]), torch.Size([5]))

A.sum(axis=[0, 1])
tensor(190.)

五、自动求导

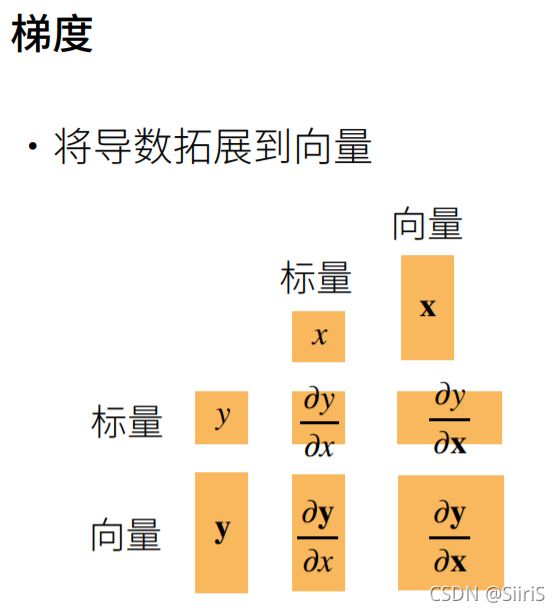
假设想对函数关于列向量x求导

import torch

x = torch.arange(4.0)
x

tensor([0., 1., 2., 3.])

在我们计算y关于x的梯度之前，我们需要一个地方来存储梯度

x.requires_grad_(True)
x.grad

计算y

y = 2 * torch.dot(x, x)
y

tensor(28., grad_fn=)

通过调用反向传播函数来自动计算y关于x每个分量的梯度

y.backward()
x.grad

tensor([ 0.,  4.,  8., 12.])

x.grad == 4 * x

tensor([True, True, True, True])

计算x的另一个函数

x.grad.zero_() y = x.sum() y.backward() x.grad  

tensor([1., 1., 1., 1.]) 

深度学习中 ，目的不是计算微分矩阵，而是批量中每个样本单独计算的偏导数之和

x.grad.zero_()
y = x * x
y.sum().backward()
x.grad

tensor([0., 2., 4., 6.])

将某些计算移动到记录的计算图之外 

  x.grad.zero_() y = x * x u = y.detach() z = u * x z.sum().backward() x.grad == u

tensor([True, True, True, True])

x.grad.zero_()
y.sum().backward()
x.grad == 2 * x

tensor([True, True, True, True])

即使构建函数的计算图需要通过Python控制流（例如，条件、循环或任意函数调用），仍然可以计算得到的变量的梯度

def f(a):
    b = a * 2
    while b.norm() < 1000:
        b = b * 2
    if b.sum() > 0:
        c = b
    else:
        c = 100 * b
    return c

a = torch.randn(size=(), requires_grad=True)
d = f(a)
d.backward()

a.grad == d / a 

tensor(True)

问题：

1、之前没有接触到过范数，一般什么时候会用到？

（此处补充范数的学习链接https://zhuanlan.zhihu.com/p/26884695）

2、对于python不熟悉的话，在跟着李沐老师学习的同时是否需要同时去学习numpy？

3、数据预处理这个过程，是否都可以套用今天讲到的这套方法？

学习感想：

其实老师讲的非常详尽，只是自己基础比较薄弱，对于线性代数知识也遗忘很多，还没有掌握高效的学习方法，只是跟着老师的代码打了一遍但是感觉没有消化吸收成为自己的知识。并且看完视频不知道如何输出，写出的学习总结非常不精炼，等于把老师讲的内容又重复了一遍，并没有产生新的感悟和知识，学习效果并不好。思考了一下解决方法，我认为可能需要多刷几遍视频，同时多观察别的同学是如何进行学习和输出的，希望自己可以慢慢摸索到其中的诀窍，做到真正的消化知识，记住知识。