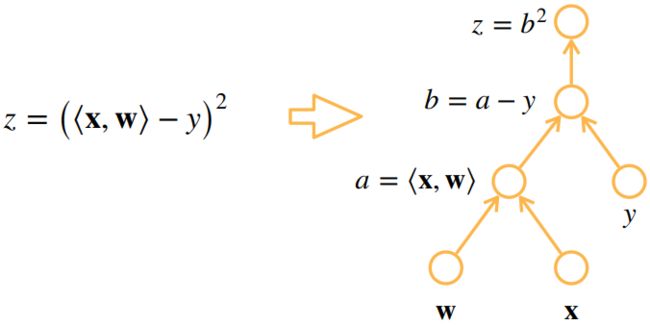李沐《动手学深度学习v2》学习笔记(一):PyTorch基础与线性代数
李沐《动手学深度学习v2》学习笔记(一):PyTorch基础与线性代数
目录:
- 李沐《动手学深度学习v2》学习笔记(一):PyTorch基础与线性代数
- 一、数据特征
-
- 1.数据格式
- 2.PyTorch基本操作
-
- 2.1 张量的创建与属性
- 2.2 张量的运算
- 2.3 张量合并
- 2.4 统计运算
- 2.5 逻辑运算
- 2.6 变换操作
- 2.7 内存问题
- 3.数据预处理
-
- 3.1 csv 文件读写
- 3.2 处理缺失值
- 3.3 数据离散化
- 二、线性代数基础
-
- 1.矩阵乘法
- 2.范数
- 3.线性代数的PyTorch实现
- 三、自动求导
-
- 1.导数相关补充
- 2.向量函数
- 3.向量求导
- 4.链式法则
- 5.自动求导
- 6.自动求导的实现
- 7.tensor.backward() 中的 gradient 参数
注: 需要熟悉使用Python,并了解Numpy、Pandas、Matplotlib等库的使用
一、数据特征
1.数据格式
N维数组是机器学习和深度神经网络的主要数据结构
| 维数 | 名称 | 实例 |
|---|---|---|
| 0-d | 标量 | 一个类别/标签 |
| 1-d | 向量 | 一个特征向量 |
| 2-d | 矩阵 | 特征矩阵 |
| 3-d | RGB图片(通道×高×宽) | |
| 4-d | 一个图片批量(批量数×通道×高×宽) | |
| 5-d | 多个视频(时间×批数数×通道×高×宽) |
注:批量数 ( b a t c h _ s i z e ) (batch\_size) (batch_size)——假设一张图片为 ( 3 , 224 , 224 ) (3,224,224) (3,224,224),如果有 1000 1000 1000 张这样的图片,则输入网络的元素个数有 1000 × 3 × 224 × 224 = 150 , 528 , 000 1000×3×224×224=150,528,000 1000×3×224×224=150,528,000 个,由于 G P U o r C P U GPU \ or \ CPU GPU or CPU 的内存有限,因此我不可能同时将这 1000 1000 1000 张图片同时输入网络,而是分成几批,例如以 100 100 100 张图片为一批,则每次批量数为 b a t c h _ s i z e = 100 batch\_size=100 batch_size=100,分 10 10 10 次来输入网络
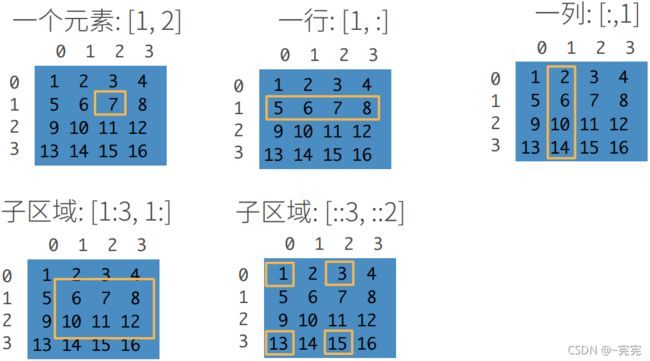
元素切片(访问):
[start:stop:step, start:stop:step],即 [ 开 始 索 引 : 结 束 索 引 : 步 长 , . . . ] [开始索引:结束索引:步长,...] [开始索引:结束索引:步长,...],维度之间用逗号分隔,访问区间为: [ s t a r t , s t o p ) [start,stop) [start,stop),其中开始索引缺省时默认从头开始,结束索引缺省时默认直到结尾,步长缺省时默认为1
2.PyTorch基本操作
# 导入Pytorch库
import torch
定义: 张量(tensor) 表示由一个数值组成的数组,这个数组可能是任意维度
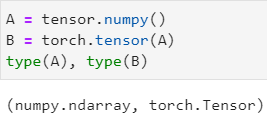
实际上,PyTorch 保留了很多与 Numpy 相同的操作,以便使用者快速上手
2.1 张量的创建与属性
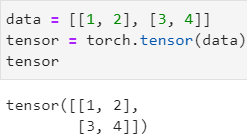
tensor = torch.tensor() 直接生成张量
tensor = torch.from_numpy() 从 numpy_array 中生成张量
tensor = torch.normal(means, std, out=None) 返回一个张量,元素值将从给定参数means,std的正态分布中抽取随机数
mean(旧版:means)一个 float \text{float} float 张量,分别对应输出元素所服从的正态分布的均值 μ \mu μ,必须指定
std一个 float \text{float} float 张量,分别对应输出元素所服从的正态分布的标准差 σ \sigma σ
size(旧版:out)默认为 None,可以指定输出张量的形状
其中mean和std必须如何如下使用规则(mean和std的形状不必匹配,当形状不同时,函数按mean的形状返回张量):
组合 输出 mean、std均为张量,且元素个数相等生成的元素服从按 mean、std中相同位置一 一对应的正态分布mean为元素个数=1的张量或浮点数,std为元素个数>1的张量所有样本抽取时共享均值,标准差按 std中的元素来生成std为元素个数=1的张量或浮点数,mean为元素个数>1的张量所有样本抽取时共享标准差,均值按 mean中的元素来生成mean、std均为浮点数按唯一的 mean、std抽取,且输出张量的形状由size决定例如:
输入:
import torch # mean、std均为张量,且元素个数相等 a = torch.normal(mean = torch.arange(1., 11.), std = torch.arange(1, 0, -0.1)) # mean为元素个数=1的张量或浮点数,std为元素个数>1的张量 c = torch.normal(mean = 0., std = torch.tensor([1., 2.])) # std为元素个数=1的张量或浮点数,mean为元素个数>1的张量 b = torch.normal(mean = torch.tensor([1., 2.]), std = 1.) # mean、std 均为浮点数 d = torch.normal(mean = 0., std = 1., size = (2, 3)) a, b, c, d输出:
tensor = torch.rand(*size, dtype, …) 返回概率符合0-1均匀分布的张量,随机
tensor = torch.randn(*size, dtype, …) 返回概率符合标准正太分布 ( μ = 0 , σ = 1 ) (\mu=0,\sigma=1) (μ=0,σ=1) 的张量,随机
tensor = torch.randint(low, high, *size) 返回在区间 [ l o w , h i g h ) [low,high) [low,high) 中随机采样的整数张量
tensor = torch.zeros(*size) 返回一个元素全为 0 0 0 的张量
tensor = torch.ones(*size) 返回一个元素全为 1 1 1 的张量
*size张量的形状,可以输入 tuple,如:(2, 2),也可以直接输入集合,如:2, 2
dtype张量的类型
tensor = torch.zeros_like(tensor) 根据张量 tensor,生成形状与 tensor 相同的全 0 0 0 张量
tensor = torch.ones_like(tensor) 根据张量 tensor,生成形状与 tensor 相同的全 1 1 1 张量
tensor = torch.arange(start, end, step) 生成区间在 [ s t a r t , s t o p ) [start,stop) [start,stop),步长为 s t e p step step 的张量,start、stop、step 可选择性缺省
tensor = torch.linspace(start, end, steps) 生成区间在 [ s t a r t , s t o p ] [start,stop] [start,stop],步长为 s t e p s steps steps 的等距张量
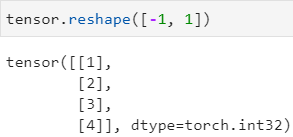
tensor.reshape() 修改张量形状,不改变顺序,"-1" 可自动分配行数
张量属性:
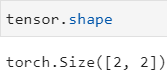
tensor.shape 张量形状
tensor.dtype 张量类型
2.2 张量的运算
张量之间可进行
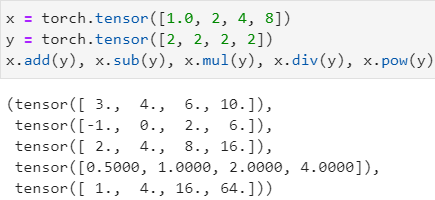
+、-、*、/、**等运算,注意要符合广播机制(broadcasting mechanism):两shape之间同一维度下的长度相等或其一长度为 1 1 1,其中*和mul()指两张量相乘(对应元素相乘)——哈达玛积,并不是矩阵点积或矩阵乘法
也可使用 tensor.add(tensor)、tensor.sub(tensor)、tensor.mul(tensor)、tensor.div(tensor)、tensor.pow(tensor),它们是等价的

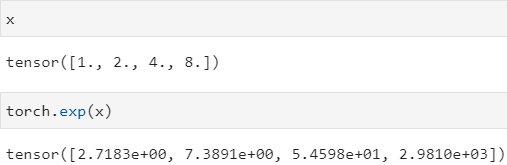
tensor = torch.exp(tensor) 对张量进行 e x p ( x ) = e x exp(x)=e^x exp(x)=ex 运算
tensor = torch.sigmoid(tensor) 对张量进行 s i g m o i d ( x ) = 1 1 + e − θ x sigmoid(x)={1 \over 1+e^{-\theta x}} sigmoid(x)=1+e−θx1 运算
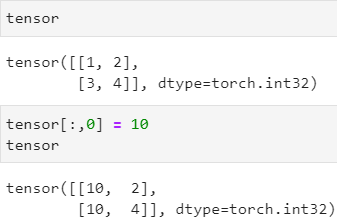
对张量的元素可直接进行赋值
2.3 张量合并
tensor = torch.cat(inputs, dim=0) 对
inputs的多个个张量进行拼接,默认dim=0
dim表示拼接方向,从 0 0 0 开始表示按 tensor 的最外部(最高维)来进行拼接,每增大 1 1 1 表示拼接维度向内部依次递进
tensor = torch.stack(inputs, dim=0) 对inputs的多个张量进行升维堆叠,默认dim=0
tensor = torch.chunk(input, chunks, dim=0) 对张量input进行不降维分块,等分为chunks块,默认dim=0


2.4 统计运算
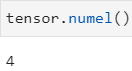
tensor.numel() 统计张量元素的个数
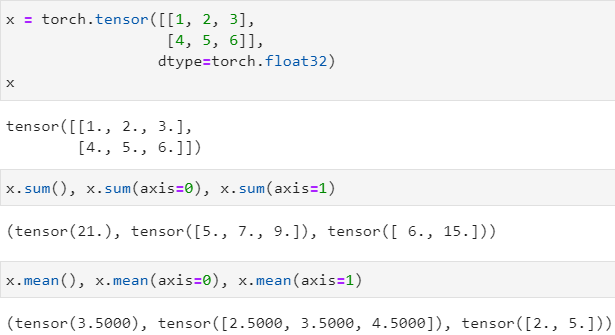
tensor.sum() 统计任意张量中所有元素的值的总和,可以指定axis来要求按维度求和
tensor.mean() 统计任意张量中所有元素的总平均值,可以指定axis来要求按维度求平均值,只能统计浮点类型
axis从 0 0 0 开始算起,按shape的顺序,axis的值是多少,就表示合并哪个维度,如:对于二维张量,若想对每一行进行求和,就是合并所有列,因此取axis=1;若想统计所有元素的值的总和,那么就要合并所有的行和列,因此取axis=[0, 1],即对哪一维求和就合并哪一维,axis就指定哪一维
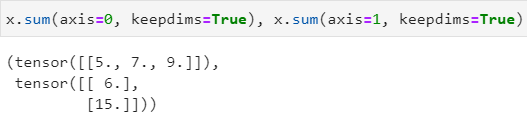
显然,上述计算过程中,计算结果丢失了维度,即原本x是二维张量,但x.sum()保存的结果是一维的,可以通过tensor.sum(keepdims=True)来保持维度不变,使被axis合并的那个维度上的元素个数为 1 1 1,保持维度不变的好处是可以使结果的广播机制不变
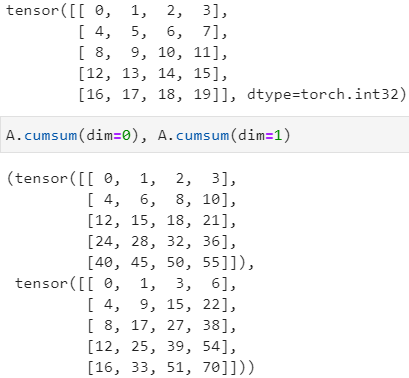
tensor.cumsum(dim) 对张量进行累加,其中dim为累加方向,必须指定,在更高版本的 PyTorch 可以使用dim或axis,它们等效
tensor.cumprod(dim) 对张量进行累乘,其中dim为累乘方向,必须指定,在更高版本的 PyTorch 可以使用dim或axis,它们等效
torch.topk(tensor, dim, k) 按dim方向统计k个最大的值及其下标
2.5 逻辑运算
2.6 变换操作
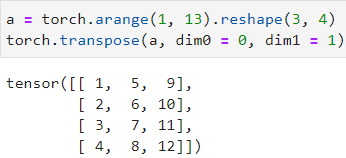
tensor = torch.transpose(tensor, dim0, dim1) 一个张量中的两个维度进行交换
tensor需要进行变换的张量
dim0、dim1需要交换的两个维度(dim)
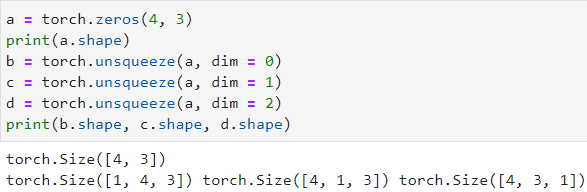
tensor = torch.squeeze(input) 维度缩减,去掉张量input中元素个数为 1 的维度,其他维度不受影响
tensor = torch.unsqueeze(input, dim=0) 维度扩张,为张量input在dim方向上扩张一个维度

tensor.reshape()、tensor.view() 矩阵形状重构
tensor.t() 实现矩阵的转置,更高版本的 PyTorch 可以使用 tensor.T 进行转置
2.7 内存问题
Python 中的内存在使用后不会自动销毁(析构),为了避免内存占用的问题,避免分配没必要的内存
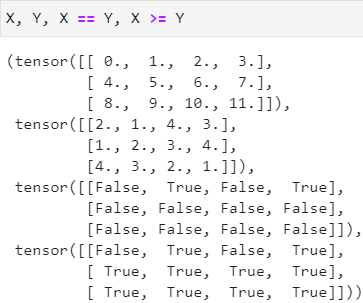
观察下面的操作,Z[:] = X + Y执行原地操作,而Z = X + Y则新建了一片新的内存,为了避免内存占用,尽量使用前一种方法来赋值

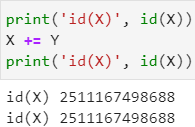
同样地,X += Y操作也不会分配新的内存,而是进行原地操作
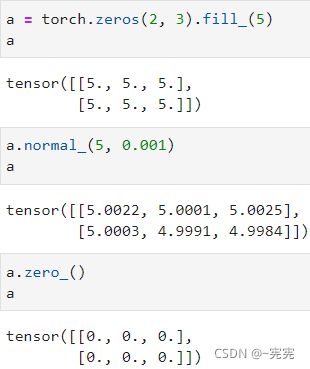
tensor = tensor.clone() 在 PyTorch 中,想要深拷贝一个张量,需要使用该方法
在 PyTorch 中一些函数包含 “_” 后缀,则说明这个函数是原地操作函数,前面所讲的许多函数都有其 “_” 版本
3.数据预处理
我们复习一下 Pandas 的数据预处理操作
3.1 csv 文件读写
写入 csv 文件:
os.makedirs(name, mode=0o777, exist_ok=False) 创建一个目录
name创建的目录名
mode目录的读写执行权限,八进制,default=0o777
exist_okFalse:若目录已存在,抛出 FileExistsError 异常;True:若目录已存在,不抛出 FileExistsError 异常
os.path.join() 拼接两个或更多的路径名组件
with open() as f: 的用法:with open('data.txt', 'r') as f: # 以 'r' 只读方式打开 data.txt 文件,文件指针为 f # data = f.read(f) 通常只使用 pandas 读取文件 with open('data.txt', 'w') as f: # 以 'w' 只写方式打开 data.txt 文件,文件指针为 f f.write('Hello World') # 写入文件
例如: 将数据以 csv 文件的方式保存在 ./data/house_tiny.csv 中
import os
# 在当前目录的上一个目录
os.makedirs(os.path.join('..', 'data'), exist_ok=True)
data_file = os.path.join('..', 'data', 'house_tiny.csv')
with open(data_file, 'w') as f:
f.write('NumRooms,Alley,Price\n')
f.write('NA,Pave,127500\n')
f.write('2,NA,106000\n')
f.write('4,NA,178100\n')
f.write('NA,NA,140000\n')
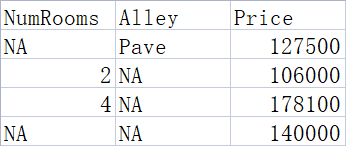
读取 csv 文件:
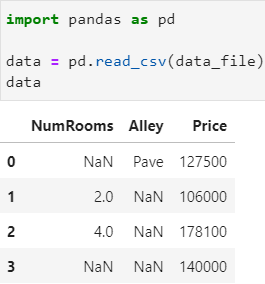
得到的是一个 Pandas 的 DataFrame 数组
3.2 处理缺失值
处理缺失值通常有两种方法,分别是:(一)插值、(二)删除
(一)插值:
data.dropna(axis=“rows”, inplace=False) 把 data 中含有缺失值 NaN 的行或列删除,注:data 必须是 Pandas 的 DataFrame 数组
axis{axis=‘rows’:删除行,axis=‘columns’:删除列,default=‘rows’}
inplace{True:直接在原地修改,False:返回一个修改后的数组,不修改原数组,default=‘False’}
(二)替换:
data.fillna(value, inplace) 分别将 data 中的缺失值 NaN 修改为value,注:data 必须是 Pandas 的 DataFrame 数组
value统一修改的值
inplace{True:直接在原地修改,False:返回一个修改后的数组,不修改原数组,default=‘False’}
例如: 仍以上面的文件为例,分别按 (一)插值、(二)删除,两种方法处理缺失值
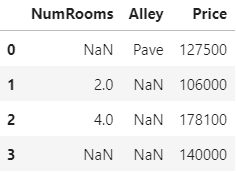
(一)删除:
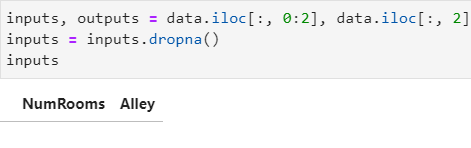
(二)插值: 通常使用平均值插值
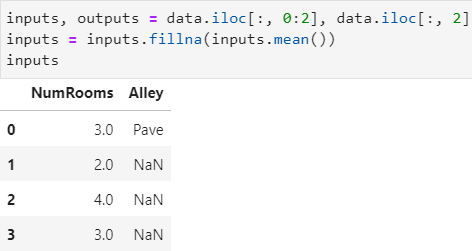
3.3 数据离散化
因为无法处理字符串,因此需要将字符串 Pava 和 NaN 视为两类,转化为数值类型或布尔类型
pd.get_dummies(data, prefix, …, dummy_na=False, …) 将
data中具有对存在有限离散分量的列进行 one-hot 编码
data数据类型:{array-like,Series,DataFrame}
prefix指定编码属性名称的前缀,default=原属性名
dummy_nabool:是否连同 Nan 一起分类?
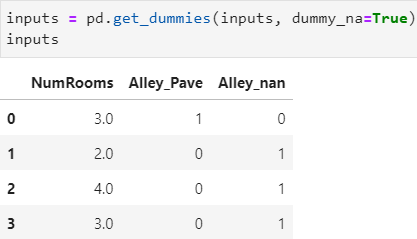
现在 inputs 和 outputs 中的所有条目都是数值类型,它们可以转换为张量格式
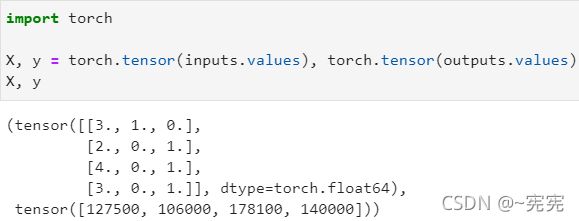
二、线性代数基础
1.矩阵乘法
矩阵相乘,左矩阵的列数必须与右矩阵的行数相等,且运算结果有如下关系:
( . . . ) i × j ( . . . ) j × k = ( . . . ) i × k \begin{pmatrix} \\ ...\\ \\ \end{pmatrix}_{i×j} \begin{pmatrix} \\ ...\\ \\ \end{pmatrix}_{j×k}= \begin{pmatrix} \\ ...\\ \\ \end{pmatrix}_{i×k} ⎝⎛...⎠⎞i×j⎝⎛...⎠⎞j×k=⎝⎛...⎠⎞i×k
(一)矩阵乘以向量:
{ b 11 t 1 + b 12 t 2 + b 13 t 3 = x 1 b 21 t 1 + b 22 t 2 + b 23 t 3 = x 2 b 31 t 1 + b 32 t 2 + b 33 t 3 = x 3 \begin{cases} b_{11}t_1+b_{12}t_2+b_{13}t_3=x_1\\ b_{21}t_1+b_{22}t_2+b_{23}t_3=x_2\\ b_{31}t_1+b_{32}t_2+b_{33}t_3=x_3 \end{cases} ⎩⎪⎨⎪⎧b11t1+b12t2+b13t3=x1b21t1+b22t2+b23t3=x2b31t1+b32t2+b33t3=x3
( b 11 b 12 b 13 b 21 b 22 b 23 b 31 b 32 b 33 ) ( t 1 t 2 t 3 ) = ( x 1 x 2 x 3 ) \begin{pmatrix} b_{11}&b_{12}&b_{13}\\ b_{21}&b_{22}&b_{23}\\ b_{31}&b_{32}&b_{33} \end{pmatrix} \begin{pmatrix} t_1\\ t_2\\ t_3 \end{pmatrix}= \begin{pmatrix} x_1\\ x_2\\ x_3 \end{pmatrix} ⎝⎛b11b21b31b12b22b32b13b23b33⎠⎞⎝⎛t1t2t3⎠⎞=⎝⎛x1x2x3⎠⎞
(二)矩阵乘以矩阵:
设有矩阵 A i × j , B j × k A_{i×j},B_{j×k} Ai×j,Bj×k,则它们相乘的结果 C j × k C_{j×k} Cj×k 中第 n n n 行,第 m m m 列的元素的计算方法为:
C n m = ∑ j A n j B j m C_{nm}=\sum_jA_{nj}B_{jm} Cnm=j∑AnjBjm
[ a 11 a 12 a 21 a 22 a 31 a 32 ] [ b 11 b 12 b 13 b 21 b 22 b 23 ] = [ a 11 b 11 + a 12 b 21 a 11 b 12 + a 12 b 22 a 11 b 13 + a 12 b 23 a 21 b 11 + a 22 b 21 a 21 b 12 + a 22 b 22 a 21 b 13 + a 22 b 23 a 31 b 11 + a 32 b 21 a 31 b 12 + a 32 b 22 a 31 b 13 + a 32 b 23 ] \left[\begin{matrix} a_{11}&a_{12}\\ a_{21}&a_{22}\\ a_{31}&a_{32} \end{matrix}\right] \left[\begin{matrix} b_{11}&b_{12}&b_{13}\\ b_{21}&b_{22}&b_{23}\\ \end{matrix}\right]= \left[\begin{matrix} a_{11}b_{11}+a_{12}b_{21}&a_{11}b_{12}+a_{12}b_{22}&a_{11}b_{13}+a_{12}b_{23}\\ a_{21}b_{11}+a_{22}b_{21}&a_{21}b_{12}+a_{22}b_{22}&a_{21}b_{13}+a_{22}b_{23}\\ a_{31}b_{11}+a_{32}b_{21}&a_{31}b_{12}+a_{32}b_{22}&a_{31}b_{13}+a_{32}b_{23} \end{matrix}\right] ⎣⎡a11a21a31a12a22a32⎦⎤[b11b21b12b22b13b23]=⎣⎡a11b11+a12b21a21b11+a22b21a31b11+a32b21a11b12+a12b22a21b12+a22b22a31b12+a32b22a11b13+a12b23a21b13+a22b23a31b13+a32b23⎦⎤
2.范数
范数,是具有“长度”概念的函数,范数是一个函数,满足正定,齐次,三角不等式的关系就称作范数,符号 ∣ ∣ w ∣ ∣ ||w|| ∣∣w∣∣ 表示范数
- 正定: ∣ ∣ w ∣ ∣ ≥ 0 ||w||\geq0 ∣∣w∣∣≥0
- 齐次: ∣ ∣ c w ∣ ∣ = ∣ c ∣ ∣ ∣ w ∣ ∣ , c ∈ R ||cw||=|c| \ ||w||,c \in R ∣∣cw∣∣=∣c∣ ∣∣w∣∣,c∈R
- 三角不等式: ∣ ∣ a + b ∣ ∣ ≤ ∣ ∣ a ∣ ∣ + ∣ ∣ b ∣ ∣ ||a+b||\leq||a||+||b|| ∣∣a+b∣∣≤∣∣a∣∣+∣∣b∣∣
范数的意义:对于标量,我们可以很直观地比较其大小,但对于向量和矩阵,我们无法像标量那样直接比较大小,而范数就是通过将矩阵或者向量映射为可以比较大小的实数,进而比较矩阵或向量的大小
(一)向量的范数: 对于 R n R^n Rn 上的向量 x = { x 1 , x 2 , . . . , x n } T ∈ R x=\{x_1,x_2,...,x_n\}^T\in R x={ x1,x2,...,xn}T∈R,有几种常用的范数
0-范数: 指向量 x x x 中的非零元素的个数,是一种度量向量稀疏性的方法
1-范数: ∣ ∣ x ∣ ∣ 1 = ∑ i = 1 n ∣ x i ∣ ||x||_1=\sum_{i=1}^n|x_i| ∣∣x∣∣1=∑i=1n∣xi∣,即向量中所有元素的绝对值之和,采用它来近似0-范数——凸优化
2-范数: ∣ ∣ x ∣ ∣ 2 = ∑ i x i 2 ||x||_2=\sqrt{\sum_{i }x_i^2} ∣∣x∣∣2=∑ixi2,即向量中所有元素的平方之和开根号,其几何意义就是向量的长度
∞ \infty ∞-范数: ∣ ∣ x ∣ ∣ ∞ = m a x ( ∣ x i ∣ ) ||x||_\infty=max(|x_i|) ∣∣x∣∣∞=max(∣xi∣),即向量中元素绝对值的最大值,称为 ∞ \infty ∞-范数或最大范数
− ∞ -\infty −∞-范数: ∣ ∣ x ∣ ∣ − ∞ = m i n ( ∣ x i ∣ ) ||x||_{-\infty}=min(|x_i|) ∣∣x∣∣−∞=min(∣xi∣),即向量中元素绝对值的最小值,称为 − ∞ -\infty −∞-范数或最小范数
p p p-范数: ∣ ∣ x ∣ ∣ p = ( ∑ i = 1 n ∣ x i ∣ p ) 1 p ||x||_p=(\sum_{i=1}^n|x_i|^p)^{1 \over p} ∣∣x∣∣p=(∑i=1n∣xi∣p)p1,即向量中所有元素的绝对值的 p p p 次方之和,再开 p p p 根号
(二)矩阵的范数: 对于 R n × m R^{n×m} Rn×m 上的矩阵 A A A,有几种常用的范数
F F F范数: ∣ ∣ A ∣ ∣ F = ∑ i j A i j 2 ||A||_{F}=\sqrt{\sum_{ij}A_{ij}^2} ∣∣A∣∣F=∑ijAij2,即矩阵 A A A 的所有元素的平方之和再开根号,较常用
1-范数: ∣ ∣ x ∣ ∣ 1 = m a x j ( ∑ i = 1 n ∣ A i j ∣ ) ||x||_1=max_j(\sum_{i=1}^n|A_{ij}|) ∣∣x∣∣1=maxj(∑i=1n∣Aij∣),即矩阵上每一列上的元素先求和,再找出和最大的那一列
∞ \infty ∞-范数: ∣ ∣ x ∣ ∣ ∞ = m a x i ( ∑ j = 1 n ∣ A i j ∣ ) ||x||_\infty=max_i(\sum_{j=1}^n|A_{ij}|) ∣∣x∣∣∞=maxi(∑j=1n∣Aij∣),即矩阵上每一行内的元素先求和,再找出和最大的那一行
2-范数: 对于 n n n 阶方阵 A A A(注:只有 n n n 阶方阵才具有2-范数), ∣ ∣ x ∣ ∣ 2 = λ 1 ||x||_2=\sqrt{\lambda_1} ∣∣x∣∣2=λ1,其中 λ 1 \lambda_1 λ1 为 A T A A^TA ATA 的最大特征值, A T A^T AT 为矩阵 A A A 的转置
定义:对于 n n n 阶方阵 A A A,存在数值 λ \lambda λ 和非零列向量 α \alpha α,使得 A α = λ α A\alpha=\lambda\alpha Aα=λα,则称 λ \lambda λ 为 A A A 的特征值, α \alpha α 为 A A A 的特征向量
A α = λ α , 即 ( . . . ) n × n ( . . . ) n × 1 = λ ( . . . ) n × 1 A\alpha=\lambda\alpha,即 \begin{pmatrix} \\ ...\\ \\ \end{pmatrix}_{n×n} \begin{pmatrix} \\ ...\\ \\ \end{pmatrix}_{n×1}=\lambda \begin{pmatrix} \\ ...\\ \\ \end{pmatrix}_{n×1} Aα=λα,即⎝⎛...⎠⎞n×n⎝⎛...⎠⎞n×1=λ⎝⎛...⎠⎞n×1
因此如果满足了 A α = λ α A\alpha=\lambda\alpha Aα=λα 的条件,那就意味着方阵 A A A 对向量 α \alpha α 的空间变换并没有改变 α \alpha α 的方向
其他性质:对称矩阵满足 A i j = A j i A_{ij}=A_{ji} Aij=Aji,反对称矩阵满足 A i j = − A j i A_{ij}=-A_{ji} Aij=−Aji
3.线性代数的PyTorch实现
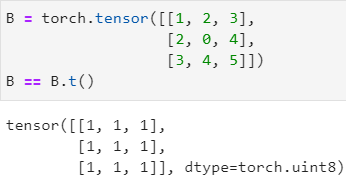
一个对称的矩阵,它和它的转置是相同的
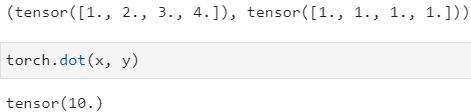
torch.dot(x, y) 实现向量的点积
torch.mv(x, y) mv——matrix vector,矩阵与向量乘积,其中x为矩阵,y为列向量(一维tensor),顺序不可调换
相当于对向量y做矩阵x的空间变换,因此运算结果也是一个向量
注:PyTorch 中的一维 tensor,从表现形式来看,是以行的形式来展现的,但从数学的习惯表达上看,它是列向量,PyTorch 中的一维数组是以列向量为数学计算约定的
torch.mm(x, y) mm——matrix matrix,矩阵与矩阵乘积,只用于二维矩阵相乘
torch.matmul(x, y) 矩阵与矩阵乘积,一般用于高维矩阵之间相乘
范数:
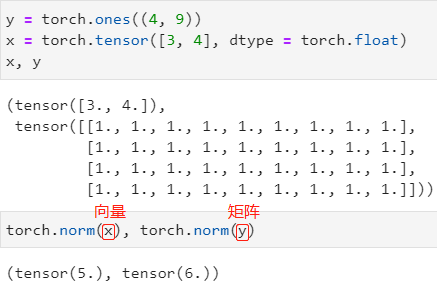
torch.norm(input) 求出input的 L 2 L_2 L2 范数(向量)或 F F F-范数(矩阵)
torch.abs(input).sum() 求出input向量的 L 1 L_1 L1 范数,PyTorch 并没有定义 L 1 L_1 L1 范数的函数,直接手动敲出即可
三、自动求导
1.导数相关补充
将导数拓展到不可微的函数——亚导数:
以 y = ∣ x ∣ y=|x| y=∣x∣ 为例,该函数在 x = 0 x=0 x=0 处不可导
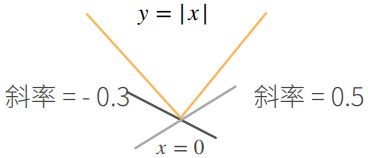
对于点 x = 0 x=0 x=0 处,我们可以添加如下定义:
∂ ∣ x ∣ ∂ x = { 1 , if x > 0 − 1 , if x < 0 a , if x = 0, a ∈ [-1, 1] \frac{\partial |x|}{\partial x}= \begin{cases} 1, & \text{if $x > 0$} \\ -1, & \text{if $x < 0$} \\ a, & \text{if $x$ = 0, a$\in$[-1, 1]} \end{cases} ∂x∂∣x∣=⎩⎪⎨⎪⎧1,−1,a,if x>0if x<0if x = 0, a∈[-1, 1]
矩阵点积:
⟨ x , y ⟩ = x T y = ∑ i = 1 n x i y i ⟶ 标 量 \langle {\bf x},{\bf y}\rangle={\bf x}^T{\bf y}=\sum_{i=1}^nx_iy_i \longrightarrow 标量 ⟨x,y⟩=xTy=i=1∑nxiyi⟶标量
2.向量函数
(一)输入标量 x x x,输出标量 f ( x ) {f(x)} f(x):
十分简单的一元函数,如: f ( x ) = x 2 + x + 1 f(x)=x^2+x+1 f(x)=x2+x+1
(二)输入向量 x {\bf x} x,输出标量 f ( x ) f({\bf x}) f(x):
输入向量,即函数是一个多元函数,具有多个自变量,如:输入 x = [ x 1 x 2 x 3 ] x=\left[\begin{matrix}x_1\\x_2\\x_3\end{matrix}\right] x=⎣⎡x1x2x3⎦⎤,输出 f ( x 1 , x 2 , x 3 ) = x 1 3 + x 2 2 + x 3 + 1 f(x_1,x_2,x_3)=x_1^3+x_2^2+x_3+1 f(x1,x2,x3)=x13+x22+x3+1,输出值一个标量
(三)输入标量 x x x,输出向量 f ( x ) → \overrightarrow{f(x)} f(x):
表示一个一元函数的输出结果是多元的,表现为一个向量,如: f ( x ) → = a x ( x 3 + x ) + a y ( x 2 ) + a z ( x + 1 ) = ( x 3 + x , x 2 , x + 1 ) → \overrightarrow {f(x)}={\bf a_x}(x^3+x)+{\bf a_y}(x^2)+{\bf a_z} (x+1)=\overrightarrow{(x^3+x, \ x^2, \ x+1)} f(x)=ax(x3+x)+ay(x2)+az(x+1)=(x3+x, x2, x+1)
上述函数也可以写成: f ( x ) → = [ f 1 ( x ) = x 3 + x f 2 ( x ) = x 2 f 3 ( x ) = x + 1 ] \overrightarrow {f(x)}=\left[\begin{matrix}f_1(x)=x^3+x\\f_2(x)=x^2\\f_3(x)=x+1\end{matrix}\right] f(x)=⎣⎡f1(x)=x3+xf2(x)=x2f3(x)=x+1⎦⎤
(四)输入向量 x {\bf x} x,输出向量 f ( x ) → \overrightarrow{f({\bf x})} f(x):
表示一个多元函数的输出结果也是多元的,如: f ( x ) → = a x ( x 3 + y ) + a y ( x 2 + z ) + a z ( x + y + z + 1 ) \overrightarrow {f({\bf x})}={\bf a_x}(x^3+y)+{\bf a_y}(x^2+z)+{\bf a_z}(x+y+z+1) f(x)=ax(x3+y)+ay(x2+z)+az(x+y+z+1)
上述函数也可以写成: f ( x ) → = [ f 1 ( x ) = x 3 + y f 2 ( x ) = x 2 + z f 3 ( x ) = x + y + z + 1 ] \overrightarrow {f({\bf x})}=\left[\begin{matrix}f_1(x)=x^3+y\\f_2(x)=x^2+z\\f_3(x)=x+y+z+1\end{matrix}\right] f(x)=⎣⎡f1(x)=x3+yf2(x)=x2+zf3(x)=x+y+z+1⎦⎤
3.向量求导
| 标量 x x x | 向量 x = [ x 1 x 2 ⋮ x 3 ] {\bf x}=\left[\begin{matrix}x_1\\x_2\\\vdots\\x_3\end{matrix}\right] x=⎣⎢⎢⎢⎡x1x2⋮x3⎦⎥⎥⎥⎤ | |
|---|---|---|
| 标量 f ( x ) f(x) f(x) | ∂ f ( x ) x \frac{\partial f(x)}{x} x∂f(x) | ∂ f ( x ) x \frac{\partial f({\bf x})}{ {\bf x}} x∂f(x) |
| 向量 f ( x ) → = [ f 1 ( x ) f 2 ( x ) ⋮ f n ( x ) ] \overrightarrow{f(x)}=\left[\begin{matrix}f_1(x)\\f_2(x)\\\vdots\\f_n(x)\end{matrix}\right] f(x)=⎣⎢⎢⎢⎡f1(x)f2(x)⋮fn(x)⎦⎥⎥⎥⎤ | ∂ f ( x ) → x \frac{\partial \overrightarrow {f(x)}}{x} x∂f(x) | ∂ f ( x ) → x \frac{\partial \overrightarrow {f({\bf x})}}{\bf x} x∂f(x) |
(一)标量 f ( x ) f(x) f(x) 对标量 x x x 求导:
即一元函数对其自变量进行微分
设 f ( x ) = x 2 + x + 1 , 则 : ∂ f ( x ) ∂ x = 2 x + 1 设 \ f(x)=x^2+x+1,则:\frac{\partial f(x)}{\partial x}=2x+1 设 f(x)=x2+x+1,则:∂x∂f(x)=2x+1
(二)标量 f ( x ) f({\bf x}) f(x) 对向量 x {\bf x} x 求导:
即多元函数在向量 x = ( x 1 , x 2 , . . . , x n ) {\bf x}=(x_1,x_2,...,x_n) x=(x1,x2,...,xn) 的方向上的方向导数,它反映了因变量在该方向上的变化率,运算结果实际上就是 f ( x ) f({\bf x}) f(x) 分别表示对自变量 { x 1 , x 2 , . . . , x n } \{x_1,x_2,...,x_n\} { x1,x2,...,xn} 求偏微分的结果
设 输 入 x = [ x 1 x 2 ⋮ x n ] ,则 f ( x ) 对 x 的方向导数为: ∂ f ( x ) ∂ x = [ ∂ f ( x ) ∂ x 1 ∂ f ( x ) ∂ x 2 ⋯ ∂ f ( x ) ∂ x n ] ,是一个行向量 设输入 \ {\bf x} =\left[\begin{matrix}x_1\\x_2\\\vdots\\x_n\end{matrix}\right]\text{,则 $f({\bf x})$ 对 ${\bf x}$ 的方向导数为:} \frac{\partial f({\bf x})}{\partial {\bf x}} =\left[\begin{matrix}\frac{\partial f({\bf x})}{\partial x_1}&\frac{\partial f({\bf x})}{\partial x_2}&\cdots&\frac{\partial f({\bf x})}{\partial x_n}\end{matrix}\right]\text{,是一个行向量} 设输入 x=⎣⎢⎢⎢⎡x1x2⋮xn⎦⎥⎥⎥⎤,则 f(x) 对 x 的方向导数为:∂x∂f(x)=[∂x1∂f(x)∂x2∂f(x)⋯∂xn∂f(x)],是一个行向量
实际上,输出行向量里的每个元素分别代表 f ( x ) f(x) f(x) 分别对 x {\bf x} x 中各输入元素的偏导数,合并成行向量指的就是方向导数
(三)向量 f ( x ) → \overrightarrow {f(x)} f(x) 对标量 x x x 求导:
即一个含多元输出的一元函数对自变量求导,相当于输出向量中的元素分别对自变量 x x x 进行求导
设 函 数 f ( x ) → = [ f 1 ( x ) f 2 ( x ) ⋮ f n ( x ) ] ,则 f ( x ) → 对 x 求导为: ∂ f ( x ) → ∂ x = [ ∂ f 1 ( x ) ∂ x ∂ f 2 ( x ) ∂ x ⋮ ∂ f n ( x ) ∂ x ] ,是一个列向量 设函数\overrightarrow {f(x)}=\left[\begin{matrix}f_1(x)\\f_2(x)\\\vdots\\f_n(x)\end{matrix}\right]\text{,则 $\overrightarrow{f(x)}$ 对 $x$ 求导为:}\frac{\partial \overrightarrow{f(x)}}{\partial x}=\left[\begin{matrix}\frac{\partial f_1(x)}{\partial x}\\\frac{\partial f_2(x)}{\partial x}\\\vdots\\\frac{\partial f_n(x)}{\partial x}\end{matrix}\right]\text{,是一个列向量} 设函数f(x)=⎣⎢⎢⎢⎡f1(x)f2(x)⋮fn(x)⎦⎥⎥⎥⎤,则 f(x) 对 x 求导为:∂x∂f(x)=⎣⎢⎢⎢⎢⎡∂x∂f1(x)∂x∂f2(x)⋮∂x∂fn(x)⎦⎥⎥⎥⎥⎤,是一个列向量
实际上,输出列向量里的每个元素分别代表 f ( x ) f({\bf x}) f(x) 中各输出元素分别对自变量 x x x 求导,然后最终结果用列向量表示
(四)向量 f ( x ) → \overrightarrow {f({\bf x})} f(x) 对向量 x {\bf x} x 求导:
表示一个含多元输出的多元函数,相当于输出向量中的元素分别对输入向量中的元素进行求导,因此它的输出结果是一个矩阵
设 输 入 x = [ x 1 x 2 ⋮ x n ] ∈ R n , 函 数 f ( x ) → = [ f 1 ( x ) f 2 ( x ) ⋮ f m ( x ) ] ∈ R m 设输入 \ {\bf x}=\left[\begin{matrix}x_1\\x_2\\\vdots\\x_n\end{matrix}\right]\in R^n,函数\overrightarrow {f({\bf x})}=\left[\begin{matrix}f_1({\bf x})\\f_2({\bf x})\\\vdots\\f_m({\bf x})\end{matrix}\right]\in R^m 设输入 x=⎣⎢⎢⎢⎡x1x2⋮xn⎦⎥⎥⎥⎤∈Rn,函数f(x)=⎣⎢⎢⎢⎡f1(x)f2(x)⋮fm(x)⎦⎥⎥⎥⎤∈Rm
则 有 : ∂ f ( x ) → ∂ x = [ ∂ f 1 ( x ) ∂ x ∂ f 2 ( x ) ∂ x ⋮ ∂ f m ( x ) ∂ x ] m × 1 = [ ∂ f 1 ( x ) ∂ x 1 ∂ f 1 ( x ) ∂ x 2 ⋯ ∂ f 1 ( x ) ∂ x n ∂ f 2 ( x ) ∂ x 1 ∂ f 2 ( x ) ∂ x 2 ⋯ ∂ f 2 ( x ) ∂ x n ⋮ ⋮ ⋱ ⋮ ∂ f m ( x ) ∂ x 1 ∂ f m ( x ) ∂ x 2 ⋯ ∂ f m ( x ) ∂ x n ] m × n 则有:\frac{\partial \overrightarrow{f({\bf x})}}{\partial {\bf x}} =\left[\begin{matrix}\frac{\partial f_1({\bf x})}{\partial {\bf x}}\\\frac{\partial f_2({\bf x})}{\partial {\bf x}}\\\vdots\\\frac{\partial f_m({\bf x})}{\partial {\bf x}}\end{matrix}\right]_{m×1} =\left[\begin{matrix}\frac{\partial f_1({\bf x})}{\partial x_1}&\frac{\partial f_1({\bf x})}{\partial x_2}&\cdots&\frac{\partial f_1({\bf x})}{\partial x_n}\\\frac{\partial f_2({\bf x})}{\partial x_1}&\frac{\partial f_2({\bf x})}{\partial x_2}&\cdots&\frac{\partial f_2({\bf x})}{\partial x_n}\\\vdots&\vdots&\ddots&\vdots\\\frac{\partial f_m({\bf x})}{\partial x_1}&\frac{\partial f_m({\bf x})}{\partial x_2}&\cdots&\frac{\partial f_m({\bf x})}{\partial x_n}\end{matrix}\right]_{m×n} 则有:∂x∂f(x)=⎣⎢⎢⎢⎢⎡∂x∂f1(x)∂x∂f2(x)⋮∂x∂fm(x)⎦⎥⎥⎥⎥⎤m×1=⎣⎢⎢⎢⎢⎡∂x1∂f1(x)∂x1∂f2(x)⋮∂x1∂fm(x)∂x2∂f1(x)∂x2∂f2(x)⋮∂x2∂fm(x)⋯⋯⋱⋯∂xn∂f1(x)∂xn∂f2(x)⋮∂xn∂fm(x)⎦⎥⎥⎥⎥⎤m×n
在输出矩阵中,每一行分别代表因变量 f ( x ) f({\bf x}) f(x) 中某一输出元素分别对 x {\bf x} x 中各输入元素的偏导数,每一列分别表示因变量 f ( x ) f({\bf x}) f(x) 中各输出元素分别对 x {\bf x} x 中某一输入元素的偏导数
上述讲解中,我们使用的是分子布局方式,因此当分子是向量时,我们需要把 x {\bf x} x 视为行向量
- 分子布局: 分子为列向量,分母为行向量(即分子不变,分母转置)
- 分母布局: 分子为行向量,分母为列向量(即分母不变,分子转置)
- 实际上,两种布局的本质是相同的,它们的区别只是矩阵的排列方式或者说结果的表达形式不同,且: (分母布局) T = 分子布局 \text{(分母布局)}^T=\text{分子布局} (分母布局)T=分子布局
总结:向量求导的本质就是——输出向量 f ( x ) ∈ R m f({\bf x}) \in R^m f(x)∈Rm 的每个元素分别对输入向量 x ∈ R n {\bf x} \in R^n x∈Rn 的每个元素求导,因此输出结果有 n × m n×m n×m 个值,即使用一个 m × n m×n m×n 的矩阵来表示
矩阵求导的常用性质:
- 设 A = [ a 1 a 2 ⋮ a n ] n × 1 x = [ x 1 x 2 ⋮ x n ] n × 1 {\bf A}=\left[\begin{matrix}a_1\\a_2\\\vdots\\a_n\end{matrix}\right]_{n×1}{\bf x}=\left[\begin{matrix}x_1\\x_2\\\vdots\\x_n\end{matrix}\right]_{n×1} A=⎣⎢⎢⎢⎡a1a2⋮an⎦⎥⎥⎥⎤n×1x=⎣⎢⎢⎢⎡x1x2⋮xn⎦⎥⎥⎥⎤n×1,若 f ( x ) = A T ⋅ x f({\bf x})={\bf A}^T·{\bf x} f(x)=AT⋅x(点积运算结果是标量,因此 f ( x ) f({\bf x}) f(x)是标量函数),则: ∂ f ( x ) ∂ x = ∂ A T ⋅ x ∂ x = A \frac{\partial {f({\bf x})}}{\partial {\bf x}}=\frac{\partial { {\bf A}^T·{\bf x}}}{\partial {\bf x}}={\bf A} ∂x∂f(x)=∂x∂AT⋅x=A(分子布局)或 A T {\bf A}^T AT(分母布局)
- 设 A {\bf A} A 是 n n n 阶方阵,即 A = [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a n 1 a n 2 ⋯ a n n ] n × n x = [ x 1 x 2 ⋮ x n ] n × 1 {\bf A} =\left[\begin{matrix}a_{11}&a_{12}&\cdots&a_{1n}\\a_{21}&a_{22}&\cdots&a_{2n}\\\vdots&\vdots&\ddots&\vdots\\a_{n1}&a_{n2}&\cdots&a_{nn}\end{matrix}\right]_{n×n}{\bf x} =\left[\begin{matrix}x_1\\x_2\\\vdots\\x_n\end{matrix}\right]_{n×1} A=⎣⎢⎢⎢⎡a11a21⋮an1a12a22⋮an2⋯⋯⋱⋯a1na2n⋮ann⎦⎥⎥⎥⎤n×nx=⎣⎢⎢⎢⎡x1x2⋮xn⎦⎥⎥⎥⎤n×1,若 f ( x ) = x T ⋅ A ⋅ x f({\bf x})={\bf x}^T·{\bf A}·{\bf x} f(x)=xT⋅A⋅x,则: ∂ f ( x ) ∂ x = A ⋅ x + A T ⋅ x = ( A + A T ) x \frac{\partial {f({\bf x})}}{\partial {\bf x}}={\bf A}·{\bf x}+{\bf A}^T·{\bf x}=({\bf A}+{\bf A}^T){\bf x} ∂x∂f(x)=A⋅x+AT⋅x=(A+AT)x
为什么要研究向量求导?
- 机器学习中数据一般是以表格来表示的,数据可以用向量来表示,如:词向量,而深度学习中大量的算法需要对数据进行求导,那么求导就转化为对矩阵求导,十分简洁,如: d f ( x ) d x = d x 2 d x {df(x) \over dx}={dx^2 \over dx} dxdf(x)=dxdx2,若是矩阵,则求导转化为 d f ( x ) d x = d x T x d x {df({\bf x}) \over d{\bf x}}={d{\bf x}^T{\bf x} \over d{\bf x}} dxdf(x)=dxdxTx
- 许多深度学习算法框架有对矩阵运算加速的支持
4.链式法则
(一)标量链式法则:
y = f ( u ) , u = g ( x ) , ∂ y ∂ x = ∂ y ∂ u ∂ u ∂ x y=f(u),u=g(x),\frac{\partial y}{\partial x}=\frac{\partial y}{\partial u}\frac{\partial u}{\partial x} y=f(u),u=g(x),∂x∂y=∂u∂y∂x∂u
(二)向量链式法则:
∂ y ∂ x = ∂ y ∂ u ∂ u ∂ x ,(1,n)=(1,)(1,n) \frac{\partial y}{\partial \bf x}=\frac{\partial y}{\partial u}\frac{\partial u}{\partial \bf x} \text{,(1,n)=(1,)(1,n)} ∂x∂y=∂u∂y∂x∂u,(1,n)=(1,)(1,n)
∂ y ∂ x = ∂ y ∂ u ∂ u ∂ x ,(1,n)=(1,k)(k,n) \frac{\partial y}{\partial \bf x}=\frac{\partial y}{\partial \bf u}\frac{\partial \bf u}{\partial \bf x} \text{,(1,n)=(1,k)(k,n)} ∂x∂y=∂u∂y∂x∂u,(1,n)=(1,k)(k,n)
∂ y ∂ x = ∂ y ∂ u ∂ u ∂ x ,(m,n)=(m,k)(k,n) \frac{\partial \bf y}{\partial \bf x}=\frac{\partial \bf y}{\partial \bf u}\frac{\partial \bf u}{\partial \bf x} \text{,(m,n)=(m,k)(k,n)} ∂x∂y=∂u∂y∂x∂u,(m,n)=(m,k)(k,n)
例如: 设 x , w ∈ R n {\bf x},{\bf w}\in R^n x,w∈Rn——列向量, y ∈ R , z = ( ⟨ x , w ⟩ − y ) 2 y\in R,z=(\langle {\bf x},{\bf w}\rangle-y)^2 y∈R,z=(⟨x,w⟩−y)2,其中 ⟨ x , w ⟩ \langle {\bf x},{\bf w}\rangle ⟨x,w⟩ 表示 x , w {\bf x},{\bf w} x,w 做内积,试计算 ∂ z ∂ w \frac{\partial z}{\partial \bf w} ∂w∂z
首先将 z z z 进行分解: a = ⟨ x , w ⟩ , b = a − y , z = b 2 a=\langle {\bf x},{\bf w}\rangle,b=a-y,z=b^2 a=⟨x,w⟩,b=a−y,z=b2,因此:
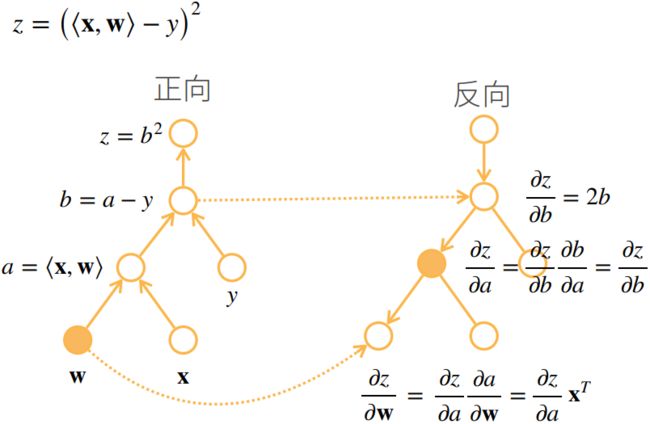
∂ z ∂ w = ∂ z ∂ b ∂ b ∂ a ∂ a ∂ w = ∂ b 2 ∂ b ∂ ( a − y ) ∂ a ∂ ⟨ x , w ⟩ ∂ w = 2 b ⋅ 1 ⋅ x T = 2 ( ⟨ x , w ⟩ − y ) x T \frac{\partial z}{\partial \bf w}=\frac{\partial z}{\partial b}\frac{\partial b}{\partial a}\frac{\partial a}{\partial \bf w} =\frac{\partial b^2}{\partial b} \ \frac{\partial (a-y)}{\partial a} \ \frac{\partial \bf \langle x,w\rangle}{\partial \bf w}=2b·1·{\bf x}^T =2(\langle x,w\rangle-y){\bf x}^T ∂w∂z=∂b∂z∂a∂b∂w∂a=∂b∂b2 ∂a∂(a−y) ∂w∂⟨x,w⟩=2b⋅1⋅xT=2(⟨x,w⟩−y)xT
其中这一步运用了矩阵求导常用性质一:
∂ ⟨ x , w ⟩ ∂ w = ∂ x T w ∂ w = x 或 x T (看布局) \frac{\partial \bf \langle x,w\rangle}{\partial \bf w}=\frac{\partial \bf x^Tw}{\partial \bf w}={\bf x} \ 或 \ {\bf x}^T\text{(看布局)} ∂w∂⟨x,w⟩=∂w∂xTw=x 或 xT(看布局)
为什么结果是 x T {\bf x}^T xT 而不是 x {\bf x} x?这是因为 ⟨ x , w ⟩ \bf \langle x,w\rangle ⟨x,w⟩是一个标量,而 w \bf w w 是一个向量,即因变量是标量,自变量是向量,因此我们按照习惯的矩阵求导布局,结果应写成行向量的形式,而 x \bf x x 是列向量,因此要写成转置的形式
例如: 设 X ∈ R m × n {\bf X}\in R^{m×n} X∈Rm×n, w ∈ R n {\bf w}\in R^n w∈Rn, y ∈ R m , z = ∣ ∣ X w − y ∣ ∣ 2 {\bf y}\in R^m,z=||{\bf Xw}-{\bf y}||^2 y∈Rm,z=∣∣Xw−y∣∣2,试计算 ∂ z ∂ w \frac{\partial z}{\partial \bf w} ∂w∂z
首先将 z z z 进行分解: a = X w , b = a − y , z = ∣ ∣ b ∣ ∣ 2 {\bf a}={\bf Xw},{\bf b}={\bf a}-{\bf y},z=||{\bf b}||^2 a=Xw,b=a−y,z=∣∣b∣∣2, ∣ ∣ b ∣ ∣ 2 ||{\bf b}||^2 ∣∣b∣∣2 表示向量的模的平方,即 b T ⋅ b {\bf b}^T·{\bf b} bT⋅b,因此:
∂ z ∂ w = ∂ z ∂ b ∂ b ∂ a ∂ a ∂ w = ∂ ∣ ∣ b ∣ ∣ 2 ∂ b ∂ ( a − y ) ∂ a ∂ X w ∂ w = 2 b T ⋅ I ⋅ X T = 2 ( X w − y ) T X \frac{\partial z}{\partial \bf w}=\frac{\partial z}{\partial {\bf b}}\frac{\partial {\bf b}}{\partial {\bf a}}\frac{\partial {\bf a}}{\partial \bf w} =\frac{\partial ||{\bf b}||^2}{\partial {\bf b}} \ \frac{\partial ({\bf a}-{\bf y})}{\partial {\bf a}} \ \frac{\partial \bf Xw}{\partial \bf {\bf w}}=2{\bf b}^T·{\bf I}·{\bf X}^T =2({\bf Xw-{\bf y}})^T{\bf X} ∂w∂z=∂b∂z∂a∂b∂w∂a=∂b∂∣∣b∣∣2 ∂a∂(a−y) ∂w∂Xw=2bT⋅I⋅XT=2(Xw−y)TX
其中 I {\bf I} I 是单位矩阵(Identiry Matrix),它是一个方阵,且主对角线的元素为 1 1 1,其他元素为 0 0 0,任意矩阵以单位矩阵相乘,等于它本身
5.自动求导
自动求导计算一个函数在指定值上的导数
- 将代码分解成操作子,每个⭕表示一个操作子(一个输入)
- 将计算表示成一个有向无环图
自动求导的两种模式:
首先根据求导的链式法则:
∂ y ∂ x = ∂ y ∂ u n ∂ u n ∂ u n − 1 ⋯ ∂ u 2 ∂ u 1 ∂ u 1 ∂ x \frac{\partial y}{\partial x} =\frac{\partial y}{\partial u_n} \ \frac{\partial u_n}{\partial u_{n-1}} \cdots \frac{\partial u_2}{\partial u_1} \ \frac{\partial u_1}{\partial x} ∂x∂y=∂un∂y ∂un−1∂un⋯∂u1∂u2 ∂x∂u1
计算上述链式法则的过程有两种方法
模式一: 正向积累,即先从 x x x 出发,先求出 ∂ u 1 ∂ x \frac{\partial u_1}{\partial x} ∂x∂u1,它和 ∂ u 2 ∂ u 1 \frac{\partial u_2}{\partial u_1} ∂u1∂u2 相乘,再往外计算
∂ y ∂ x = ∂ y ∂ u n ( ∂ u n ∂ u n − 1 ( ⋯ ( ∂ u 2 ∂ u 1 ∂ u 1 ∂ x ) ) ) \frac{\partial y}{\partial x} =\frac{\partial y}{\partial u_n}(\frac{\partial u_n}{\partial u_{n-1}}(\cdots(\frac{\partial u_2}{\partial u_1} \ \frac{\partial u_1}{\partial x}))) ∂x∂y=∂un∂y(∂un−1∂un(⋯(∂u1∂u2 ∂x∂u1)))
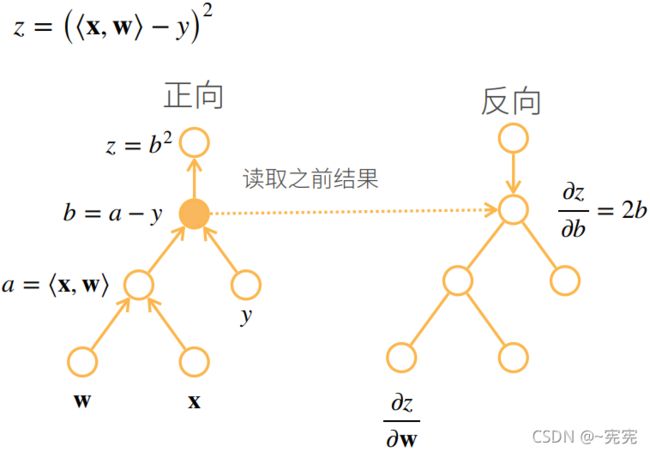
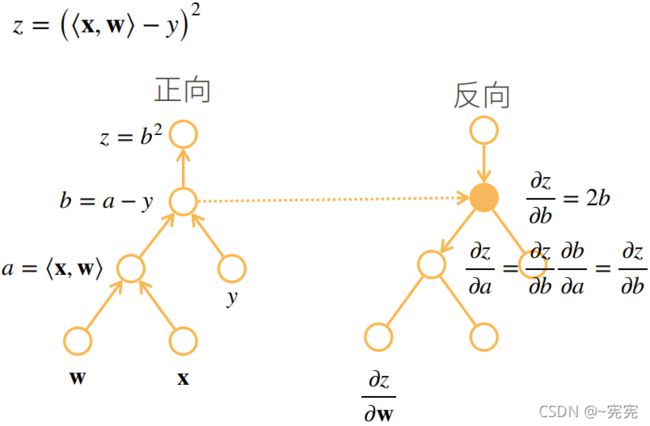
模式二: 反向传播(Back Propagation-BP),即先计算封装程度最高的部分,即 ∂ y ∂ u n \frac{\partial y}{\partial u_n} ∂un∂y,再向内部进行求导
∂ y ∂ x = ( ( ( ∂ y ∂ u n ∂ u n ∂ u n − 1 ) ⋯ ) ∂ u 2 ∂ u 1 ) ∂ u 1 ∂ x \frac{\partial y}{\partial x} =(((\frac{\partial y}{\partial u_n} \ \frac{\partial u_n}{\partial u_{n-1}})\cdots)\frac{\partial u_2}{\partial u_1})\frac{\partial u_1}{\partial x} ∂x∂y=(((∂un∂y ∂un−1∂un)⋯)∂u1∂u2)∂x∂u1
- 它是经典的 BP神经网络(BPNN) 所采用的求导方法
反向传播计算图:
6.自动求导的实现
tensor.backward(gradient=None) 由因变量调用,求梯度,默认是反向传播方式求导
gradient当函数的因变量是非标量时,需要指定该参数
例如: 对函数 y = 2 x T x y=2{\bf x}^T{\bf x} y=2xTx 关于列向量 x {\bf x} x 求导
在默认情况下,PyTorch 会累积梯度,因此,在进行下一次梯度计算前,我们需要清除之前的值
tensor.grad.zero_() 清除梯度累积,由自变量调用
例如: 清除上一例中的梯度积累,重新计算 y = x . s u m ( ) y={\bf x}.sum() y=x.sum() 的梯度
∵ x = [ x 1 x 2 x 3 x 4 ] = [ 0. 1. 2. 3. ] , x . s u m = x 1 + x 2 + x 3 + x 4 , ∴ ∂ y ∂ x = ∂ ( x . s u m ( ) ) ∂ x = [ ∂ ( x 1 + x 2 + x 3 + x 4 ) ∂ x 1 ⋯ ∂ ( x 1 + x 2 + x 3 + x 4 ) ∂ x 4 ] = [ 1. 1. 1. 1. ] ∵{\bf x} =\left[\begin{matrix}x_1\\x_2\\x_3\\x_4\end{matrix}\right] =\left[\begin{matrix}0.\\1.\\2.\\3.\end{matrix}\right],{\bf x}.sum =x_1+x_2+x_3+x_4,∴\frac{\partial y}{\partial {\bf x}} =\frac{\partial ({\bf x}.sum())}{\partial {\bf x}} =\left[\begin{matrix}\frac{\partial (x_1+x_2+x_3+x_4)}{\partial x_1}&\cdots&\frac{\partial (x_1+x_2+x_3+x_4)}{\partial x_4}\end{matrix}\right]=\left[\begin{matrix}1.&1.&1.&1.\end{matrix}\right] ∵x=⎣⎢⎢⎡x1x2x3x4⎦⎥⎥⎤=⎣⎢⎢⎡0.1.2.3.⎦⎥⎥⎤,x.sum=x1+x2+x3+x4,∴∂x∂y=∂x∂(x.sum())=[∂x1∂(x1+x2+x3+x4)⋯∂x4∂(x1+x2+x3+x4)]=[1.1.1.1.]
深度学习中,我们很少对向量函数求导,即很少对返回值为非标量的函数求导,求导常用在求 L o s s Loss Loss 函数的梯度,而它是个标量函数
如果是向量函数,我们通常计算批量中每个样本单独计算的偏导数之和
其中 ∗ * ∗ 表示哈达玛积,即:
∵ x = [ x 1 x 2 x 3 x 4 ] = [ 0. 1. 2. 3. ] , y = x ∗ x = [ x 1 2 x 2 2 x 3 2 x 4 2 ] , ∴ ∂ y ∂ x = [ ∂ x 1 2 ∂ x 1 ∂ x 1 2 ∂ x 2 ⋯ ∂ x 1 2 ∂ x n ∂ x 2 2 ∂ x 1 ∂ x 2 2 ∂ x 2 ⋯ ∂ x 2 2 ∂ x n ⋮ ⋮ ⋱ ⋮ ∂ x 3 2 ∂ x 1 ∂ x 3 2 ∂ x 2 ⋯ ∂ x 3 2 ∂ x n ] 4 × 4 ∵{\bf x} =\left[\begin{matrix}x_1\\x_2\\x_3\\x_4\end{matrix}\right] =\left[\begin{matrix}0.\\1.\\2.\\3.\end{matrix}\right],{\bf y}={\bf x}*{\bf x} =\left[\begin{matrix}x_1^2\\x_2^2\\x_3^2\\x_4^2\end{matrix}\right],∴\frac{\partial {\bf y}}{\partial {\bf x}} =\left[\begin{matrix}\frac{\partial x_1^2}{\partial x_1}&\frac{\partial x_1^2}{\partial x_2}&\cdots&\frac{\partial x_1^2}{\partial x_n}\\\frac{\partial x_2^2}{\partial x_1}&\frac{\partial x_2^2}{\partial x_2}&\cdots&\frac{\partial x_2^2}{\partial x_n}\\\vdots&\vdots&\ddots&\vdots\\\frac{\partial x_3^2}{\partial x_1}&\frac{\partial x_3^2}{\partial x_2}&\cdots&\frac{\partial x_3^2}{\partial x_n}\end{matrix}\right]_{4×4} ∵x=⎣⎢⎢⎡x1x2x3x4⎦⎥⎥⎤=⎣⎢⎢⎡0.1.2.3.⎦⎥⎥⎤,y=x∗x=⎣⎢⎢⎡x12x22x32x42⎦⎥⎥⎤,∴∂x∂y=⎣⎢⎢⎢⎢⎢⎡∂x1∂x12∂x1∂x22⋮∂x1∂x32∂x2∂x12∂x2∂x22⋮∂x2∂x32⋯⋯⋱⋯∂xn∂x12∂xn∂x22⋮∂xn∂x32⎦⎥⎥⎥⎥⎥⎤4×4而 y . s u m ( ) = x 1 2 + x 2 2 + x 3 2 + x 4 2 , ∴ ∂ ( y . s u m ( ) ) ∂ x = [ ∂ ( x 1 2 + x 2 2 + x 3 2 + x 4 2 ) ∂ x 1 ⋯ ∂ ( x 1 2 + x 2 2 + x 3 2 + x 4 2 ) ∂ x 4 ] = [ 2 x 1 2 x 2 2 x 3 2 x 4 ] = [ 0. 2. 4. 6. ] 而 \ {\bf y}.sum()=x_1^2+x_2^2+x_3^2+x_4^2,∴\frac{\partial ({\bf y}.sum())}{\partial {\bf x}} =\left[\begin{matrix}\frac{\partial (x_1^2+x_2^2+x_3^2+x_4^2)}{\partial x_1}&\cdots&\frac{\partial (x_1^2+x_2^2+x_3^2+x_4^2)}{\partial x_4}\end{matrix}\right] =\left[\begin{matrix}2x_1&2x_2&2x_3&2x_4\end{matrix}\right] =\left[\begin{matrix}0.&2.&4.&6.\end{matrix}\right] 而 y.sum()=x12+x22+x32+x42,∴∂x∂(y.sum())=[∂x1∂(x12+x22+x32+x42)⋯∂x4∂(x12+x22+x32+x42)]=[2x12x22x32x4]=[0.2.4.6.]
tensor = tensor.detach() 返回一个新 tensor,从当前计算图中分离下来,把它作为叶子节点,它在求导时被视为常数,不再参与求导
注:返回的 tensor 仍指向原 tensor 的存放位置,即它们处于同一内存,被指定后这个 tensor 永远不需要计算梯度,不具有grad,即使之后重新将它的requires_grad置为True,它也不会具有梯度grad,这样就可以继续使用这个新的 tensor 进行计算,当之后要进行反向传播时,到该调用了detach()的 tensor 就会停止,不能再继续向前进行传播
例如: 可以将某些计算移动到计算图之外,以后在反向传播计算 L o s s Loss Loss 的梯度时会用到
发现在计算梯度时,由于u = y.detach(),因此u在求导时被视为常数
Python 控制流:即每次运算时,PyTorch 会在背后把它运算过程的计算图存储下来,以计算梯度:
函数function_flow最终的结果为 f ( a ) = 2 n a f(a)=2^na f(a)=2na 或 f ( a ) = ( 2 n + 100 ) a f(a)=(2^n+100)a f(a)=(2n+100)a,因此求导后就是前面的常数: f ( a ) a f(a) \over a af(a)
with torch.no_grad(): 在它内部进行的所有运算,不会加入计算图
7.tensor.backward() 中的 gradient 参数
当函数的因变量为非标量时,那么对求该函数调用 backward() 时得到的并非梯度,而是一个矩阵
例如: 仍以 x = [ x 1 x 2 x 3 x 4 ] = [ 0. 1. 2. 3. ] , y = x ∗ x {\bf x}=\left[\begin{matrix}x_1\\x_2\\x_3\\x_4\end{matrix}\right]=\left[\begin{matrix}0.\\1.\\2.\\3.\end{matrix}\right],{\bf y}={\bf x}*{\bf x} x=⎣⎢⎢⎡x1x2x3x4⎦⎥⎥⎤=⎣⎢⎢⎡0.1.2.3.⎦⎥⎥⎤,y=x∗x 为例,求 y {\bf y} y 对 x {\bf x} x 的梯度
首先求出 y {\bf y} y,发现它是一个 4 × 1 4×1 4×1 矩阵,即为非标量输出
y = [ x 1 x 2 x 3 x 4 ] ∗ [ x 1 x 2 x 3 x 4 ] = [ y 1 = x 1 2 y 2 = x 2 2 y 3 = x 3 2 y 4 = x 4 2 ] 4 × 1 {\bf y} =\left[\begin{matrix}x_1\\x_2\\x_3\\x_4\end{matrix}\right]*\left[\begin{matrix}x_1\\x_2\\x_3\\x_4\end{matrix}\right]=\left[\begin{matrix}y_1=x_1^2\\y_2=x_2^2\\y_3=x_3^2\\y_4=x_4^2\end{matrix}\right]_{4×1} y=⎣⎢⎢⎡x1x2x3x4⎦⎥⎥⎤∗⎣⎢⎢⎡x1x2x3x4⎦⎥⎥⎤=⎣⎢⎢⎡y1=x12y2=x22y3=x32y4=x42⎦⎥⎥⎤4×1
对 y {\bf y} y 求梯度,有:
∂ y ∂ x = [ ∂ y 1 ∂ x 1 ∂ y 1 ∂ x 2 ∂ y 1 ∂ x 3 ∂ y 1 ∂ x 4 ∂ y 2 ∂ x 1 ∂ y 2 ∂ x 2 ∂ y 2 ∂ x 3 ∂ y 2 ∂ x 4 ∂ y 3 ∂ x 1 ∂ y 3 ∂ x 2 ∂ y 3 ∂ x 3 ∂ y 3 ∂ x 4 ∂ y 4 ∂ x 1 ∂ y 4 ∂ x 2 ∂ y 4 ∂ x 3 ∂ y 4 ∂ x 4 ] = [ 2 x 1 0 0 0 0 2 x 2 0 0 0 0 2 x 3 0 0 0 0 2 x 4 ] = [ 0. 0 0 0 0 1. 0 0 0 0 4. 0 0 0 0 6. ] \frac{\partial {\bf y}}{\partial {\bf x}} =\left[\begin{matrix}\frac{\partial y_1}{\partial x_1}&\frac{\partial y_1}{\partial x_2}&\frac{\partial y_1}{\partial x_3}&\frac{\partial y_1}{\partial x_4}\\ \frac{\partial y_2}{\partial x_1}&\frac{\partial y_2}{\partial x_2}&\frac{\partial y_2}{\partial x_3}&\frac{\partial y_2}{\partial x_4}\\ \frac{\partial y_3}{\partial x_1}&\frac{\partial y_3}{\partial x_2}&\frac{\partial y_3}{\partial x_3}&\frac{\partial y_3}{\partial x_4}\\ \frac{\partial y_4}{\partial x_1}&\frac{\partial y_4}{\partial x_2}&\frac{\partial y_4}{\partial x_3}&\frac{\partial y_4}{\partial x_4}\end{matrix}\right] =\left[\begin{matrix}2x_1&0&0&0\\ 0&2x_2&0&0\\ 0&0&2x_3&0\\ 0&0&0&2x_4\end{matrix}\right] =\left[\begin{matrix}0.&0&0&0\\ 0&1.&0&0\\ 0&0&4.&0\\ 0&0&0&6.\end{matrix}\right] ∂x∂y=⎣⎢⎢⎢⎡∂x1∂y1∂x1∂y2∂x1∂y3∂x1∂y4∂x2∂y1∂x2∂y2∂x2∂y3∂x2∂y4∂x3∂y1∂x3∂y2∂x3∂y3∂x3∂y4∂x4∂y1∂x4∂y2∂x4∂y3∂x4∂y4⎦⎥⎥⎥⎤=⎣⎢⎢⎡2x100002x200002x300002x4⎦⎥⎥⎤=⎣⎢⎢⎡0.00001.00004.00006.⎦⎥⎥⎤
实际上就是因变量 y {\bf y} y 的每个输出分别对每个自变量 x {\bf x} x 求导
当指定 gradient=torch.ones(4)即 gradient ← tensor([1, 1, 1, 1]) 时,就相当于进行了如下运算:
[ 1 1 1 1 ] [ 0. 0 0 0 0 1. 0 0 0 0 4. 0 0 0 0 6. ] = [ 0. 1. 4. 6. ] \left[\begin{matrix}1&1&1&1\end{matrix}\right] \left[\begin{matrix}0.&0&0&0\\ 0&1.&0&0\\ 0&0&4.&0\\ 0&0&0&6.\end{matrix}\right] =\left[\begin{matrix}0.\\1.\\4.\\6.\end{matrix}\right] [1111]⎣⎢⎢⎡0.00001.00004.00006.⎦⎥⎥⎤=⎣⎢⎢⎡0.1.4.6.⎦⎥⎥⎤
其中,左边的矩阵就是 gradient 所指定的矩阵,我们可以将它视为分别是 y {\bf y} y 中四个输出通道分别对 x {\bf x} x 中某一输入元素求偏导的权重大小,当它为全 1 1 1 矩阵时,表示所有通道的偏导数之和
因此,y.sum().backward() 就等效于 y.backward(torch.ones(len(x)))
参考资料:
[1]Search 动手学深度学习课程