数据结构-应用场景

栈和队列

栈的常见应用场景

当我们我们要处理的数据只涉及在一端插入和删除数据，并且满足 后进先出（LIFO, Last In First Out） 的特性时，我们就可以使用栈这个数据结构。

• 递归

• 实现浏览器的回退和前进功能，需要两个栈

• 检查括号是否成对出现，
  思想：从左往右依次扫描，“（” 进，“）” 取栈顶元素进行判断

• 反转字符串：将字符串中的每个字符先入栈再出栈就可以了。

• 维护函数调用：最后一个被调用的函数必须先完成执行，符合栈的 后进先出 特性。

队列常见应用场景

当我们需要按照一定顺序来处理数据的时候可以考虑使用队列这个数据结构。

• 阻塞队列
  何为阻塞？
  当队列为空的时候，出队操作阻塞，当队列满的时候，入队操作阻塞。使用阻塞队列我们可以很容易实现“生产者 - 消费者“模型

• 线程池中的请求/任务队列
  线程池中没有空闲线程时，新的任务请求线程资源时，线程池会将这些请求放在队列中，当有空闲线程的时候，会从队列中获取任务交给空闲线程执行
  分为两种实现方式：

  • 基于链表的实现方式，可以实现一个支持无限排队的无界队列，
  • 而基于数组实现的有界队列，队列的大小有限

• 数据库连接池等待队列

• Linux 内核进程等待队列

• 消息队列

树

B/B+树

大量应用在数据库和文件系统当中。
它的设计思想是，将相关数据尽量集中在一起，以便一次读取多个数据，减少硬盘操作次数。
B树算法减少定位记录时所经历的中间过程，从而加快存取速度。

哈夫曼树：文件压缩

红黑树

红黑树的关键性质: 内部保证有序，由于不用严格平衡所以旋转开销小

1）java8 hashmap中链表转红黑树。时间复杂度从O(n)降到O(logn)

2） epoll在内核中的实现，用红黑树管理文件描述符fd。
为什么?

1. 因为fd变动十分频繁(变动就需要旋转，而红黑树的旋转开销小)，且需要支持快速查询(红黑树查询速度O(logN))，所以红黑树很适合。
2. 红黑树可以判断是否是重复的fd

字典/trie/前缀树

1、有一个1G大小的一个文件，里面每一行是一个词，词的大小不超过16字节，内存限制大小是1M。返回频数最高的100个词。

类似这种问题可以利用字典树求解，扫描文件时建立字典树，字典树的每条边记录一个字母，节点中记录两个值，

• 一个是从根节点到当前节点的所有字母组成的单词word
• 一个是这个单词出现的次数count。每当一个词的最后一个字母对应一个节点时，count++

最后，扫描完文件之后，遍历这个字典树取出count大小在前100的节点的word属性即可。
时间复杂度：O(n*len) n为单词数量，len为单词平均长度。

2、1000万字符串，其中有些是重复的，需要把重复的全部去掉，保留没有重复的字符串。请怎么设计和实现？
可以利用字典树求解，扫描文件时建立字典树，字典树的每条边记录一个字母，节点中记录两个值，

• 一个是从根节点到当前节点的所有字母组成的单词word
• 一个是记录这个word是否已经出现过的flag。

当某个单词的最后一个字母对应一个节点时，这个节点的flag=true。之后再有单词的最后一个字母对应这个节点时。就将这个单词去掉即可。

3、2亿QQ号中查找出某一个特定的QQ号
字典树

海量数据

1、Hash

拆分大文件为多个小文件

比如现在有10亿条数据，我们创建 10 个空文件 ，遍历这 10 亿个关键词，并且通过某个哈希算法对其求哈希值，然后哈希值%10，得到的结果就是这个搜索关键词应该被分到的文件编号。

求TOPK

把一个大的集合通过哈希函数分配到多个文件里，然后统计每个小文件中每一种数出现的次数 ， 这样我们就得到了所有小文件中各自出现次数最多的数， 还有各自的次数统计。接下来只需要选出小文件各自的第一名中谁出现的次数最多即可。

根据哈希函数的性质， 同一种数不可能被哈希到不同的小文件上.所以不用担心计算出错

2、堆

无序数组求TOPK

• 小根堆求最大TOPK
• 大根堆求最小TOPK

我们可以维护一个大小为 K 的小顶堆，顺序遍历数组，从数组中取出数据与堆顶元素比较。

• 如果比堆顶元素大，我们就把堆顶元素删除，并且将这个元素插入到堆中；
• 如果比堆顶元素小，则不做处理，继续遍历数组。

这样等数组中的数据都遍历完之后，堆中的数据就是前 K 大数据了。

遍历数组需要 O(n) 的时间复杂度，一次堆化操作需要 O(logK) 的时间复杂度，所以最坏情况下，n 个元素都入堆一次，所以时间复杂度就是 O(nlogK)。

优先队列

1. 合并多个有序小文件成为一个大文件

假设我们有 100 个小文件，每个文件中存储的都是有序的字符串。我们希望将这些 100 个小文件合并成一个有序的大文件。这里就会用到优先级队列。

2. 高性能定时器

假设我们有一个定时器，定时器中维护了很多定时任务，每个任务都设定了一个要触发执行的时间点。

我们就可以用优先级队列来解决。我们按照任务设定的执行时间，将这些任务存储在优先级队列中，队列首部（也就是小顶堆的堆顶）存储的是最先执行的任务。

利用堆求中位数

• 对于一组静态数据，中位数是固定的，直接排序取n/2即可，尽管排序的代价比较大，但是边际成本会很小。

• 如果是动态数据集合，中位数在不停地变动，如果再用先排序的方法，每次询问中位数的时候，都要先进行排序，那效率就不高了。借助堆这种数据结构，我们不用排序，就可以非常高效地实现求中位数操作。

具体怎么做？
我们需要维护两个堆，一个大顶堆，一个小顶堆。

• 大顶堆中存储前半部分数据，

• 小顶堆中存储后半部分数据，且小顶堆中的数据都大于大顶堆中的数据。

• 如果 n 是偶数，大顶堆中的堆顶元素就是我们要找的中位数。

• 如果 n 是奇数，大顶堆就存储 n/2+1 个数据，小顶堆中就存储 n/2 个数据。

数据是动态变化的，当新添加一个数据的时候，我们如何调整两个堆，让大顶堆中的堆顶元素继续是中位数呢？

• 如果新加入的数据<=大顶堆的堆顶元素，我们就将这个新数据插入到大顶堆；
• 如果新加入的数据>=小顶堆的堆顶元素，我们就将这个新数据插入到小顶堆。

这时两个堆中的数据个数不符合前面约定的情况怎么办？
我们可以从一个堆中不停地将堆顶元素移动到另一个堆，通过这样的调整，来让两个堆中的数据满足上面的约定。

时间复杂度

• 插入数据因为需要涉及堆化，所以时间复杂度变成了 O(logn)，
• 但是求中位数我们只需要返回大顶堆的堆顶元素就可以了，所以时间复杂度就是 O(1)。

实际上，利用两个堆不仅可以快速求出中位数，还可以快速求其他百分位的数据，原理是类似的。

比如：如何快速求接口的 99% 响应时间？
假设当前总数据的个数是 n，大顶堆中保存 n*99% 个数据，小顶堆中保存 n*1% 个数据。
大顶堆堆顶的数据就是我们要找的 99% 响应时间。

3、位图bitmap：是否出现/去重

位图适用于大规模数据，但数据状态又不是很多的情况。通常是用来判断某个数据是否存在。

位图其实是用数组实现的，数组的每一个元素的每一个二进制位都可以表示一个数据的某种状态

4、布隆过滤器：从n里面筛除m个

对于网页黑名单系统、垃圾邮件过滤系统、爬虫的网址判重系统等，加上系统容忍一定程度的失误率， 但是对空间要求比较严格， 那么很可能使用布隆过滤器。

布隆过滤器的优势就在于使用很少的空间就可以将准确率做到很高的程度。

布隆过滤器如何工作的？
利用bitmap和hash函数
假设有一个长度为m的bitarray数组
再假设一共有k个哈希函数， 这些函数的输出域S 都>=m， 并且这些哈希函数都足够优秀， 彼此之间也完全独立。 那么对同一个输入对象。经过k个哈希函数算出来的结果也是独立的，可能相同，也可能不同，但彼此独立。对算出来的每一个结果都对m取余 （ %m ）， 然后在bitarray上把相应的位置设置为1（涂黑）， 如图:

我们把bit类型的数组记为bitMap。 至此， 一个输入对象对bitMap的影响过程就结束了，也就是bitMap中的一些位置会被涂黑。 接下来按照该方法处理所有的输入对象，每个对象都可能把bitMap中的一些白位置涂黑，也可能遇到己经涂黑的位置，遇到已经涂黑的位置让其继续为黑即可。 处理完所有的输入对象后，可能bitMap中己经有相当多的位置被涂黑。 至此， 一个布隆过滤器生成完毕， 这个布隆过滤器代表之前所有输入对象组成的集合

那么在检查阶段时， 如何检查某一个对象是否是之前的某一个输入对象呢？
假设一个对象为a，想检查它是否是之前的输入对象，就把a通过k个哈希函数算出k个值，然后把 k个值取余（%m）， 就得到在［0，m-1］范围上的k个值。 接下来在bitMap上看这些位置是不是都为黑。

• 如果有一个不为黑， 说明a 一定不在这个集合里。
• 如果都为黑， 虽然不是一定，但就认为a 在这个集合里。

例题

1、假设现在我们有一个包含 10 亿个搜索关键词的日志文件，如何快速获取到 Top 10 最热门的搜索关键词呢？

看到TOPK，立马想到 散列表和堆

1、散列表
顺序扫描这 10 亿个搜索关键词。当扫描到某个关键词时，我们去散列表中查询。

• 如果不存在，我们就将它插入到散列表，并记录次数为 1。
• 如果存在，我们就将对应的次数+1；

以此类推，等遍历完这 10 亿个搜索关键词之后，散列表中就存储了不重复的搜索关键词以及出现的次数。

2、小顶堆
建立一个大小为 10 的小顶堆，遍历散列表，依次取出每个搜索关键词及对应出现的次数，然后与堆顶的搜索关键词对比。

• 如果出现次数比堆顶搜索关键词的次数多，那就删除堆顶的关键词，将这个出现次数更多的关键词加入到堆中。
• 如果少就pass

以此类推，当遍历完整个散列表中的搜索关键词之后，堆中的搜索关键词就是出现次数最多的 Top 10 搜索关键词了。

进阶 ：无法一次性将所有的搜索关键词加入到内存中。这个时候该怎么办呢？
将 10 亿条搜索关键词先通过哈希算法分片到 10 个文件中，对这 10 亿个关键词分片之后，每个文件都只有 1 亿的关键词，我们针对每个包含 1 亿条搜索关键词的文件，利用散列表和堆，分别求出 Top 10，然后把这个 10 个 Top 10 放在一块，然后取这 100 个关键词中，出现次数最多的 10 个关键词，这就是这 10 亿数据中的 Top 10 最频繁的搜索关键词了。

2、40亿个非负整数中找到没出现的数
32位无符号整数的范围是0～4294967295， 现在有 个正好包含40亿个无符号整数的 文件 ， 所以在整个范围中必然有没出现过的数。
内存限制为10MB， 但是只用找到一个没出现过的数即可。

首先，0～4294967295这个范围是可以平均分成64个区间的，每个区间是67108864个数
如果统计落在每一个区间上的数有多少，肯定有至少一个区间上的计数少于67108864。利用这一点可以找出其中一个没出现过的数。具体过程为：

• 第一次遍历时，先申请长度为64的整型数组countArr[0… 63], countArr[i用来统计区间 i 上的数有多少。遍历40亿个数，根据当前数是多少来决定哪个区间上的计数增加。必然有某个位置上的值小于 67108864，则这个区间上必然有值未出现，比如说是第37区间

• 然后申请长度为67108864的bitmap，这占用大约8MB的空间。再遍历一次40亿个数，此时的遍历只关注落在第37区间上的数，记为num（num/ 67108864==37），其他区间的数全部忽略。
  如果步骤2的num在第37区间上，将bitArr[num-67108864*37］的值设置为1，也就是只做第37区间上的数的bitArr映射。遍历完40亿个数之后，在bitArr上必然存在没被设置成1的位置，假设第i个位置上的值没设置成1，那么67108864×37+i这个数就是一个没出现过的数。

3、40亿个非负整数中找到出现两次的数
32位7G符号整数的范围是0～4294967295，砚在有40亿个无符号整数，可以使用最多 IGB的内存，找出所有出现了两次的数。

可以用bitmap的方式来表示数出现的情况，用2个位置表示一个数出现的词频。

• 如果初次遇到num，就把bitArr［num2+ l］和bitArr[num2］设置为01，
• 如果第二次遇到num，就把bitArr［num2+ l］和bitArr[num2］设置为10，
• 如果第三次遇到num，就把bitArr［num2+ l］和bitArr[num2］设置为11。

遍历完成后，再依次遍历bitArr，如果发现bitArr［num2+ l］和bitArr[num2] 为01，那么i就是出现了两次的数。

4、可以使用最多10MB的内存，怎么找到这40亿个整数的中位数？

申请个长度为2148的无符号整型数组arr[0… 2147]，把40亿个整数分为2148个区间， arr[i表示第 i 区间有多少个数。
arr必然小于10MB。然后遍历40亿个数，如果遍历到当前数为num，先看num落在哪个区间上（num/2M），然后将对应的进行arr[num/2M++操作。这样遍历下来，就得到了每一个区间的数的出现状况，通过累加每个区间的出现次数，就可以找到40亿个数的中位数（也就是第20亿个数）到底落在哪个区间上。

不能用大小堆，10M内存放不下。

设计题

实现LRU

cache 这个数据结构必要的条件：

1、显然 cache 中的元素必须有时序，以区分最近使用的和久未使用的数据，当容量满了之后要删除最久未使用的那个元素腾位置。

2、我们要在 cache 中快速找某个 key 是否已存在并得到对应的 val；

3、每次访问 cache 中的某个 key，需要将这个元素变为最近使用的，也就是说 cache 要支持在任意位置快速插入和删除元素。

那么，什么数据结构同时符合上述条件呢？

哈希表查找快，但是数据无固定顺序；链表有顺序之分，插入删除快，但是查找慢。
所以结合一下就是 散列表hashMap+双向链表

java中有哈希链表 LinkedHashMap。但是手撕时不要直接用，而是自己实现

LRU 缓存算法的核心数据结构就是哈希链表，双向链表和哈希表的结合体。这个数据结构长这样：

2、数组
效率太低，每次都要移动整个数组。

如何存储微博、微信等社交网络中的好友关系？

微博用有向图，微信是无向图

微博

用什么存储结构？

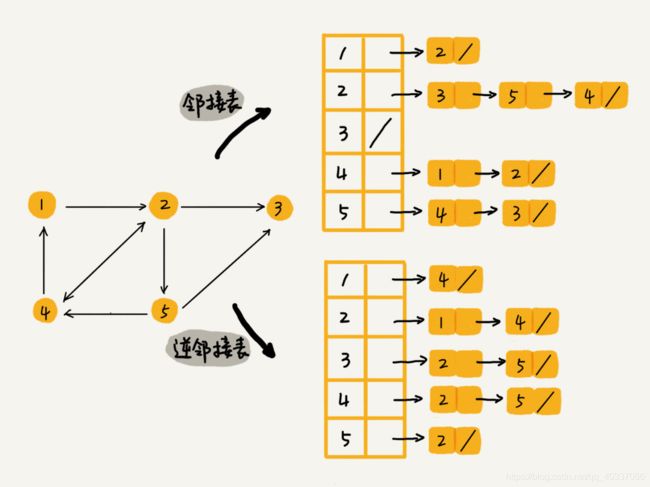
存储结构有 邻接矩阵和邻接表。因为社交网络是一张稀疏图，使用邻接矩阵存储比较浪费存储空间。所以，这里我们采用邻接表来存储。

不过，用一个邻接表来存储这种有向图是不够的。我们去查找某个用户关注了哪些用户非常容易，但是如果要想知道某个用户都被哪些用户关注了，也就是用户的粉丝列表，是非常困难的。

基于此，我们需要一个逆邻接表。

• 邻接表中存储了用户的关注关系，
• 逆邻接表中存储的是用户的被关注关系。

基础的邻接表不适合快速判断两个用户之间是否是关注与被关注的关系，所以我们选择改进版本，将邻接表中的链表改为支持快速查找的动态数据结构。选择哪种动态数据结构呢？红黑树、跳表、有序动态数组还是散列表呢？

因为我们需要按照用户名称的首字母排序，分页来获取用户的粉丝列表或者关注列表，用跳表这种结构再合适不过了。
这是因为，跳表插入、删除、查找都非常高效，时间复杂度是 O(logn)，空间复杂度上稍高，是 O(n)。最重要的一点，跳表中存储的数据本来就是有序的了，分页获取粉丝列表或关注列表，就非常高效。

如果对于小规模的数据，比如社交网络中只有几万、几十万个用户，我们可以将整个社交关系存储在内存中，上面的解决思路是没有问题的。但是如果像微博那样有上亿的用户，数据规模太大，我们就无法全部存储在内存中了。这个时候该怎么办呢？

哈希算法将数据分片，将邻接表存储在不同的机器上。逆邻接表的处理方式也一样。当要查询顶点与顶点关系的时候，我们就利用同样的哈希算法，先定位顶点所在的机器，然后再在相应的机器上查找。

微信好友

1、微信的好友关系是稀疏矩阵，为了减少空间浪费，使用邻接表；
2、为了提高查找效率，将邻接表中的链表改为支持快速查找的动态数据结构，这里使用红黑树、跳表都可以，考虑到好友列表是按照字母排序的，可以使用跳表