C++八股文分享---数据结构其一---树(二叉树、二叉搜索树、AVF树、红黑树、B树与B+树、赫夫曼树)
八股文分享 — 数据结构树(二叉树、二叉搜索树、AVL树、红黑树、B树与B+树、赫夫曼树)
#前言
树是一种非常典型的数据结构,无论是面试还是对于日常开发来讲,都是一个应该理解透彻的数据结构。部分树应该掌握到可手撕,较复杂的树应知道内部实现原理。本文需要对树结构有一定了解,不会细致的分享每一种数据结构的基础知识,只分享我在复习过程中认为重要的知识点。
一、二叉树
二叉树的特点为任意节点至多有2个孩子子节点。对于二叉树,我们要掌握如下知识点:
1、二叉树的前序遍历、中序遍历、后序遍历:
递归实现:
/*该代码为伪代码仅表示代码思路。如下伪代码为中序遍历,对于前序和后序遍
历只需要调整第14行代码的位置即可,在开头则为前序遍历,在结尾为后续遍历*/
void visitTree(Tree* root)
{
if(root == nullptr)
{
return;
}
else
{
visitTree(root->left);
/*
对当前节点的操作步骤
如打印当前节点数据printf("%s\n",root->data);
*/
visitTree(root->right);
}
}
2、二叉树的层序遍历
方法:使用栈辅助存放当前节点,实现层次遍历
力扣参考题目:102. 二叉树的层序遍历
3、二叉树的序列化与反序列化
方法:序列化使用前序遍历即可,输出每个节点数据组成字符串;反序列化使用栈来记录每个创捷节点的当前孩子节点的空闲个数,具体直接参考力扣相关例题。
掌握程度要求:熟练手撕
力扣参考题目:297. 二叉树的序列化与反序列化
二、二叉搜索树
二叉搜索树的重要特质为,在二叉树的基础上增加了左子树的所有值应都小于根节点的值,右子树的所有值应都大于根节点的值。乍看二叉搜索树的访问效率很高,最大的遍历次数为树的高度,最小的遍历次数为1。
但实际存在某种特殊情况,比如根节点只有一个右孩子,然后剩下的全部元素为一条直线向下排列在左子树,造成分部不均匀,查找和插入效率几乎等同于线性结构。如下图:

掌握程度要求:熟练手撕
力扣参考题目:96. 不同的二叉搜索树、98. 验证二叉搜索树
三、AVL树
AVL树的特点:
节点的平衡因子为其左子树高度减右子树的高度。当设定平衡因子为1时,任意节点的左子树高度
减右子树高度差的绝对值应小于等于1,若为该值大于1则意味着要重新调整二叉树为平衡二叉树。
调整时会旋转树,最终使每个节点的左子树高度与右子树高度差在平衡因子规定的范围内。
掌握程度要求:了解原理
对于AVL树的概念还不了解的小伙伴可以参考下面的文章,讲的非常详细。
AVF树的详解:动画 | 什么是AVL树?
转载来自:CSDN-程序员吴师兄
四、红黑树
红黑树的特点:
节点为红色或黑色
根节点为黑色,所有叶子节点为均是为null的黑色节点
从根节点到任意叶子节点所经过的黑色节点数目相同
从根节点到任意叶子节点的最远距离不会超过最短距离的2倍
红黑树是二叉查找树,是一种弱平衡树
掌握程度要求:了解原理
对于红黑树的概念不了解的小伙伴可参考下面文章,非常可爱的漫画讲解。红黑树是个非常烧脑的知识点,但是这篇文章讲的真的非常棒。
红黑树的详解:动画 | 什么是AVL树?
转载来自:CSDN-Timegoeson
五、B树与B+树
B树和B+树的出现是因为磁盘IO操作。当磁盘数据较大时,我们不能一次性加载所有数据,只能逐一加载磁盘页,每个磁盘页对应树的节点。造成大量磁盘IO操作(最坏情况下为树的高度),若磁盘页管理使用平衡二叉树,会由于深度太大造成大量IO操作,因此发明了B树和B+树来解决这个问题。
B树:
B树摒弃了二叉树,改为多叉树,目的就是减小树的深度
B树的具有阶的性质,为所有节点孩子个数的最大值。
B树的每个节点包含K-1个元素,以及K个孩子,且ceil(m/2) ≤ k ≤ m
节点元素的值从左到右依次增加
B+树:
有k个子树的中间节点包含有k个元素(B树中是k-1个元素),每个元素不保存数据,只用来索引
,所有数据都保存在叶子节点。
所有的叶子结点中包含了全部元素的信息,及指向含这些元素记录的指针,且叶子结点本身依关键
字的大小自小而大顺序链接。
所有的中间节点元素都同时存在于子节点,在子节点元素中是最大(或最小)元素。
B+树相较B树的优势:
1、B+树的节点只存储索引,数据全在叶子节点,因此B+树查找元素的效率相较稳定,都需遍历到叶子节点;而B树的数据分布在各个节点,因此B树在查询数据时最理想的情况为根节点就查到,最差情况为遍历到叶子节点,因此效率不稳定;
图为3阶B树:
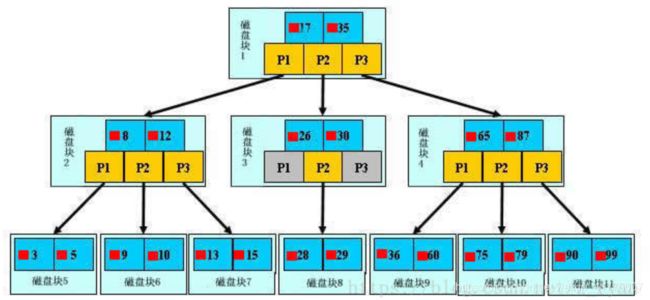
2、在需要遍历某个区间的多个元素时,B树需要逐个元素的遍历,效率很低,若是在磁盘数据读取的情景中会造成多次的IO操作;而B+树只需要遍历到区间下限元素,然后使用叶子节点的链表结构向右依次遍历即可,效率提升明显。
图为同样数据的3阶B+树:
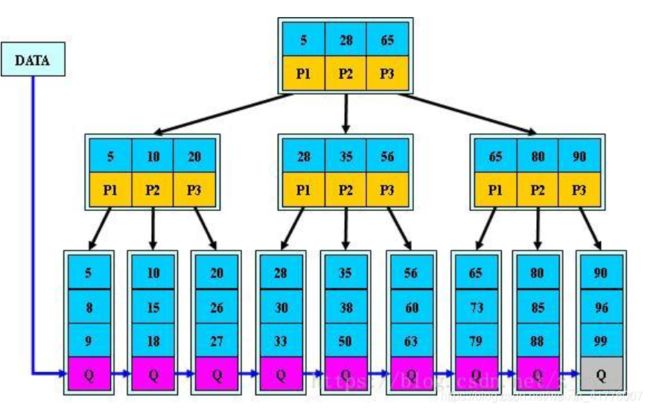
掌握程度要求:了解原理
对于B树和B+树想了解更多的小伙伴可以参考下面的文章,一篇文章搞懂B树与B+树。
B树与B+树的详解:简单剖析B树(B-Tree)与B+树
转载来自:CSDN-z_ryan
六、赫夫曼树
赫夫曼树也是二叉树的一种。在原有二叉树的基础上增加了节点权值的概念。在此先说明以下几个概念:
1、结点的路径长度:从根节点到该结点的路径上的连接数。
2、树的路径长度:树中每个叶子结点的路径长度之和。
3、结点带权路径长度:结点的路径长度与结点权值的乘积。
4、树的带权路径长度:WPL(Weighted Path Length)是树中所有叶子结点的带权路径长度之和。
而霍夫曼树霍夫曼树就是一颗带权二叉树使其树的带权路径长度最小的最优解。
如下图为一个场景,使用树来存储一个班级的成绩分布。而成绩占比就可以理解为该节点的权值。在下图构建的二叉树中,70%的学生分数在70-89区间,意味着70%的学生成绩通过概树查询要从根节点经过3个路径才能到达,即从根节点触发右->右->左,得到成绩等级为良好,但这样效率是很低的。我们可不可以把良好区间提到靠近根节点,这样来减少70%成绩等级为良好的查询速度呢?
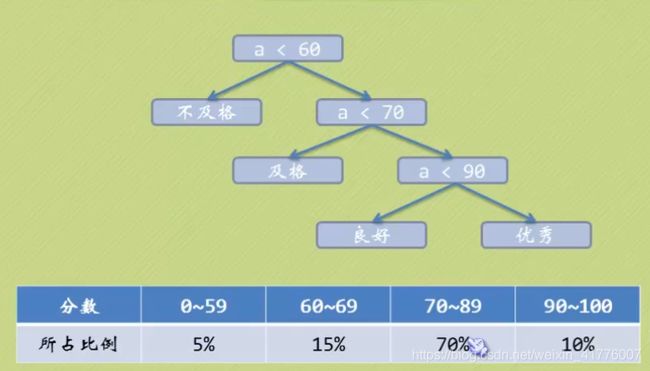
如下图为上述场景改良的带权二叉树,很明显此时查询成绩等级为良好的效率提升了,从根节点触发左->右即可到达良好。而这正是一个霍夫曼树应用的场景,霍夫曼树就是一颗带权二叉树使其树的带权路径长度最小的最优解。
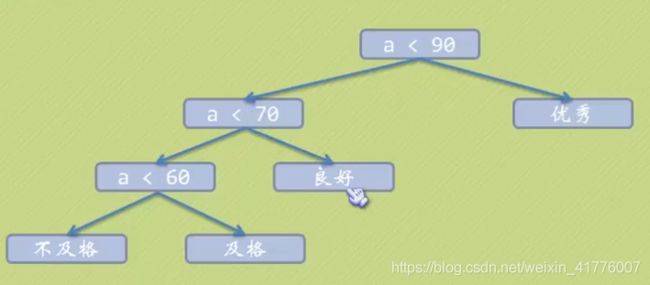
霍夫曼树的应用主要体现在文件压缩,通过使用原始数据构建一颗节点为字符、节点权重代表字符出现频率的赫夫曼树,然后对需要加密的数据使用该赫夫曼树进行加解密。
感兴趣的小伙伴可以参考小甲鱼的数据结构与算法视频(P52-P54),其中详细介绍了霍夫曼编码的实现:赫夫曼编码
掌握程度要求:了解原理
持续更新中…
