注意力机制+Swin-Transformer详解
注意力机制与Swin-Transformer
本文内容和图片未经允许禁止盗用,转载请注出处。
一、摘要
本文包括两个部分,第一部分主要介绍注意力机制的思想,并详细讲解注意力机制、自注意力机制和多头注意力机制的区别和本质原理,第二部分将详细讲解SWin-Transformer的网络结构,算法策略。最后总结Transformer应用于视觉领域的现状和发展。对注意力机制有一定了解的同学可以直接看第二部分,看SWin-Transformer是通过什么样的策略解决掉在图像上计算多头注意力的高复杂度问题。
二、注意力机制
注意力机制可以认为是一种权重分配机制,我们人类在观察眼前的景象时,大脑会自动关注我们希望关注的区域,而忽略与我们不相关的区域,这就是一种大脑的注意力机制,我们给希望关注的区域分配更多的权重,给不相关的区域分配更少的比重,以此来快速得到我们想要了解的内容。
以一张图为例,看图问问题(query):

- 请描述这个人的样貌
- 请描述这个人的动作
对于第一个问题,我们大脑会着重看这个人的脸部特征,包括五官,戴眼镜,留胡须,而对于图片上的其他区域,我们不会关心背后墙是什么颜色,桌前是否有电脑,因为这些区域并不会帮助我们准确地描述这个人的样貌。再比如第二个问题,我们大脑会着重关注这个人的姿态,包括胳膊支撑在椅子上,手指摸着额头,眼睛注视着电脑,同样地,对于图片上的其他区域,我们不会去过多关注,因为这些区域也不能帮助我们回答第二个问题。其实人脑本身就有极强的注意力机制。
那我们如何通过数学去量化和描述这种注意力机制呢,下面主要介绍三种常见的机制。
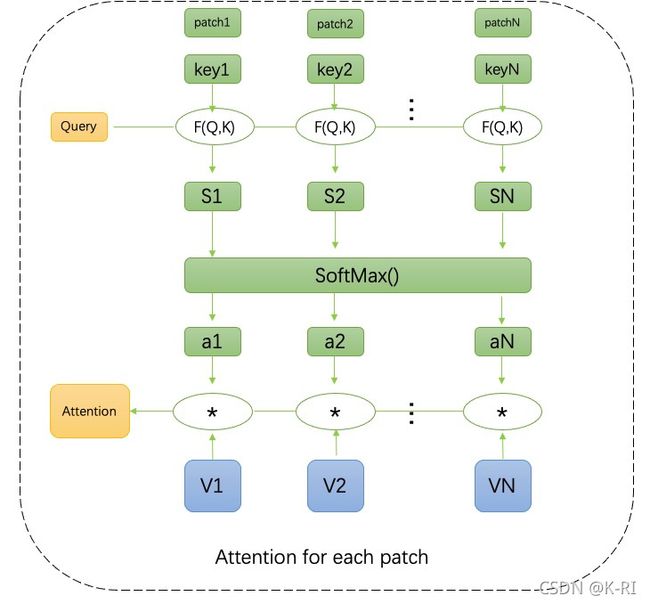
以上图那个男人为例,将图像分割成多个patch,我们想通过计算Attention的方式回答上述两个问题,就需要引入三个向量,Query(查询向量),Key(键向量),Value(值向量)
简单理解,将Q(查询向量)当作我们target问题的一个答案向量,key-value向量对代表着source的每个元素,这里的source就是输入图像,我们要计算当前Q对应于source的Attention值,就是先将Q和K做运算求两者的相似性(最常见的方法:1.求两向量的点积,点积越大,重合度越高,越相关;2,求cos相似性,夹角越小越相似;3.引入Mlp线性相关)。相似性的值经过softmax归一化转化成0-1之间的权重值。最后根据权重系数对Value进行加权求和。
那么qkv三向量是怎么来的呢,其实在运算的过程中还有三个权重矩阵WQ,WK,WV,这三个权重向量右乘输入经过embedding后得到的嵌入向量后,得到qkv三向量。在反向更新权重时,更新的就是WQ,WK,WV三个权重矩阵。
从上述计算过程就可以体会,注意力机制本质上是通过QK之间的相似度值来对V进行调制,相似度越高,对V的调制就越强,相似度越低,对V的调制就越弱。
- 用于找到单位各个元素之间内部关联的self-attention
自注意力机制顾名思义就是对自身的每个元素计算attention值,得到每个元素与其余所有元素之间的相关权重。也可以看成是source=target的普通注意力机制。
为什么要算自注意力机制呢,这里以nlp的例子来解释:
上述两句话,如果单纯用普通attention计算,我们可能不会准确的知道it指代的是谁,但是计算self-attention,我们就可以知道第一句的it与horse关系很强,第二句的it与river关系很强。
如果你懂了自注意力机制,那么多个self-attention合并加权得到的就是multi-head attention。
多头注意力机制增强了self-attention关注多个位置的能力,并且它给出了attention的多个“表示子空间(representation subspaces)“
下面是两种机制的计算过程。
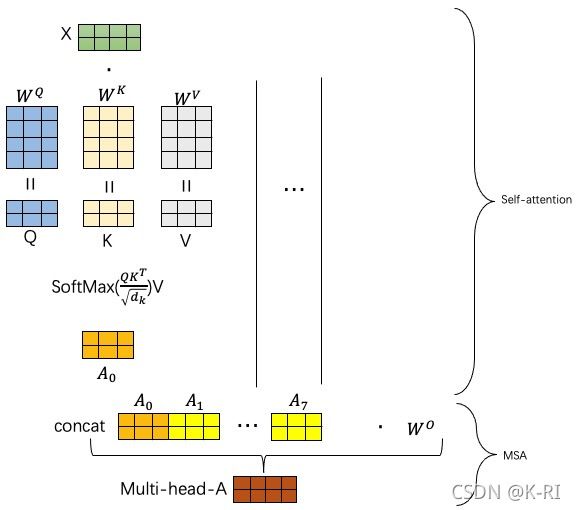
在多头机制下,每个头有独立的权重矩阵和QKV矩阵,一般包括8个头,就可以得到8个不同的A矩阵。而mlp层的输入应该是一个矩阵,所以需要把8个矩阵拼接在一起,然后用另外的权重矩阵WO乘积,结果就是一个融合了所有自注意力信息的矩阵。
以上就是注意力机制的所有内容,下一部分将详解SWin-Transformer。
三、Swin-Transformer
在SWin-Transformer之前,其实已经出现了将Transformer运用于视觉的网络,如VIT,DETR等,虽然在视觉任务上的表现基本可以与Faster-Rcnn相当,但计算复杂度却比CNN高的多,训练速度也相当慢,这是由于这些网络都是在图像全局计算多头注意力。论文指出,这种全局计算注意力机制的算法复杂度与输入图像大小的平方成正比。
SWin-Transformer提出了基于windows计算注意力的方法,这种方法其实更像是一种训练策略,而非颠覆性的算法。这种策略一方面大大降低了attention在图像上的计算复杂度,另一方面也设计了一种类似CNN的层级结构,使得它可以成为视觉任务的主干网络。
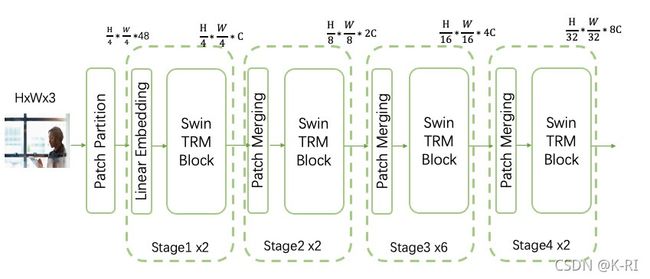
首先输入是一张3通道的图像,经过Patch切分模块将图像切割,每个Patch大小为4X4,将切割的图像送入embedding层,得到嵌入向量。关于embedding层可以参考nlp的embedding操作,原理是一样的,主要原理就是通过一个映射矩阵将原始输入降维或升维,目的就是将一个稀疏矩阵稠密化,压缩向量空间。嵌入向量经过stage1的two-swin-TRM-block后,通道没变,继续经过stage2,在这之前,多了一个Patch-Merging层,目的是为了模拟CNN的卷积层去降低分辨率,将stage1的分辨率降低2*2倍,数据总量不变,stage2输出的通道就应该是4C,但实际输出是2C,原因就是在输出前加了一个全连接层,将通道由4C变为2C,之后重复stage2多次。
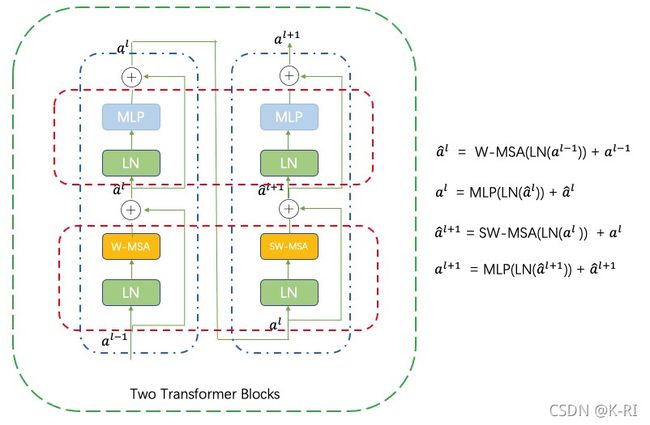
上图包含两个transformer,其实不要觉得复杂,不管是这种结构还是Encoder-Decoder结构,本质上都是计算多头注意力机制,如果你能彻底搞懂本文第一部分的内容,无论结构怎么变,对于你都应该是相当简单。
主要组件就是W-MSA、SW-MSA、LN和MLP,所有的transformer结构都是一个多头注意力机制连一个前馈网络MLP,只不过在这两个组件之前要多加一个Layer-Norm层,再加一个残差连接。
而swin-transformer的创新策略就是W-MSA、SW-MSA,本质上是计算MSA,但不像VIT计算全局MSA,而是基于windows和shfit-windows计算MSA。
左图将图像划分为4个window,右图将图像划分为9个window,这么做是为了得到左图划分的4个window的内部联系,可以看到右图划分的每个窗口都包含了左图的至少两个区域。通过这种划分方法增强了独立窗口之间的联系。但在计算MSA时,9个窗口的计算量比4个窗口的多了2.25倍,只有将窗口数控制在与左图相同的情况下,才能并行的计算MSA,为此,又提出了一种cyclic-shift策略:

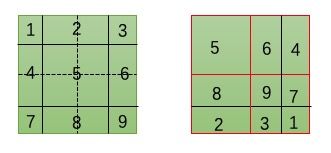
如上图,通过roll操作,将中间与原始window相同大小的D循环移位到1位置,重新将9个窗口划分为4个窗口(蓝色线),但在除1以外的三个区域,都包含了多个不同的原始区域,我们希望在计算MSA时针对相同的原始区域去计算,所以要增加mask操作,但具体在矩阵的哪些位置设置mask呢
5区域是不需要mask的,因为在windows_size里只有5,而(6,4),(8,2),(1,3,7,9)都是混合的,在计算self-attention时,行列相同的值才保留,不同的位置都置为-100,以使得计算softmax时的值趋近于0,以达到mask的目的。以(6,4)为例,mask设置为:

其他组合不再赘述。计算完shift之后,需要把结果还原传给下一阶段。到这里,SW-MSA的计算过程就结束了。
以上就是Swin-TRM的全部内容,还有一个与VIT不同的是,VIT在计算embedding的同时,增加了一个位置编码,与embedding的结果一同送给后面的TRM,而这里是在计算MSA的时候加了一个相对位置编码,所以总attention公式为:

具体的编码方式可以参考源码理解,这里不再赘述。
四、总结
注意力机制其实更适合用于视觉领域,因为它这种根据权重去分配资源的能力与人脑类似,而anchor_base 的策略依然是通过不同长宽比的先验框遍历图像的各种可能来得到我们想要了解的区域,所以从本质上来讲,注意力机制更符合我们认识世界的规律。
由于基于全局的MSA计算复杂度相当高,而且不能模拟人眼的多尺度视野,导致TRM早期无法取得与CNN相同的效果。而SWin-TRM可以说初步解决了视觉的这两个难点,但它一定不会是最优的策略,从实验结果来看,在庞大的公开数据集上的表现提高了一个点,其实并不能说明什么问题,所以我认为它只是一个从CNN到TRM为主干的过渡结构,TRM运用在视觉上还有很长的路要走。