10种常见排序算法（c++）

看别的代码总是感觉难受，因此自己写一下加深印象，也方便以后复习

总览

先把这个表背下来
每个排序算法的平均时间复杂度和空间复杂度
最重要的：插排，堆排，归并，快排

选择排序

这是最简单也最没用的一种排序方式，因为时间复杂度非常高而且不稳定，基本在工程上用不上这个东西；

思想

思想就是一遍又一遍过滤这个数组，然后把最小的放到前面去：
比如5，3，2，4，1第一次找到1，1跟第一个5换位置，
然后从第二个开始找找最小的放到第二个位置
依次进行直到倒数第二个。

代码

class solution
{
     
    void emplace_front(vector<int>& nums, int i)//前插vector
    {
     
        int size = nums.size();
        vector<int> tempvec;
        tempvec.reserve(size + 1);//防止搬运
        tempvec.push_back(i);
        for (auto it : nums)
        {
     
            tempvec.push_back(it);
        }
        nums = tempvec;
    }
public:
    void mysort(vector<int>& nums)
    {
     
        int size = nums.size();

        for (int j = 0; j < size; j++)
        {
     
            auto it = nums.begin() + j;
            int tempnum = nums[j];
            for (int i = j+1 ; i < size; i++)
            {
     
                if (tempnum < nums[i])//从大到小从左到右塞入，因此结果递增
                {
     
                    tempnum = nums[i];
                    it = nums.begin() + i;
                }
            }
            nums.erase(it);
            emplace_front(nums, tempnum);
            //值得注意的是erase不仅仅原有容器中的迭代器失效，迭代器本身也会失效
            //之前写错了，应该直接交换两个的位置，时间复杂度为常数，空间复杂度也为常数，就不改了，就当熟悉一下stl，喝咖啡不适合敲代码
        }
    }

};

测试

int main()
{
     
    vector<int> test{
      1,3,2,5,4,8,6,9 };
    solution mysolution;
    mysolution.mysort(test);
    for (auto it : test)
    {
     
        cout << it << "\t";
    }
    cout << endl;
    system("pause");
}

结果
当然有些人也可以用对数器进行验证，我比较懒就不写了，就是随机产生组数据，然后用自带的sort函数和我们写的进行对比，如果不相等输出false，大概就这么个思路。后面都不写测试了，但是楼主都会测，保证代码可以正确使用；

分析

初始化，打印结果不计入时间复杂度
空间复杂度为1，时间复杂度为n平方
说这个不稳定啊，其实我上面这样写是稳定的，因为我是头插，稳不稳定就看对原来的顺序有没有被打乱，如果是直接交换两者的位置就是不稳定的，当然上面的已经不是严格意义上的选择排序了。

优化空间：
同时找出最大和最小的两组数，一个放前面一个放后面，这样时间复杂度降低一半。

冒泡排序

思想

不断对比相邻的两个数，把大的放到右边，
总的顺序从0——n-1，到0——n-2……；

代码

#include
#include
using namespace std;
class solution
{
     
public:
    void mysort(vector<int>& nums)
    {
     
        int size = nums.size();
        for (int i = 0; i < size; i++) 
        {
     
            for (int j = 1; j <size-i ; j++) 
            {
     
                if (nums[j] < nums[j - 1]) 
                {
     
                    swap(nums[j], nums[j - 1]);
                }
            }
        }
    }
};

代码很简单就不说明了；

分析

时间复杂度 n方，空间复杂度为1，因为两两比较因此稳定
最好时间复杂度为n，但是这里是还是n方，
改进方式：
循环的时候加一个flag对是否已经排好队进行验证，如果没有发生任何交换，直接return掉，如果有发生交换才继续，这样最好时间复杂度就是n

插入排序

思想

从0开始，对每一个找到的数跟他前面的进行对比，如果比前面的小，就一直换；

代码

#include
#include
using namespace std;
class solution
{
     
public:
    void mysort(vector<int>& nums)
    {
     
        int size = nums.size();
        for (int i = 1; i < size; i++) 
        {
     
            int j = i;
            while (j>=1&&nums[j - 1] > nums[j]) 
            {
     
                swap(nums[j - 1], nums[j]);
                --j;
            }
        }
    }
};

分析

也可以把这个值进行临时存储，然后把前面的大于它的数往后挪，直到不大于的时候直接赋值；
空间复杂度1，时间复杂度n方，其实比之前的冒泡和选择快一点点；
三种简单排序就到此为止；
优化：
**双插入排序：**一下子找俩数，一个小的一个大的，小的网里面查，大的直接查小的后面就行，少了很多比较的过程

总结：
冒泡基本不用，因为太慢了，
选择基本不用，因为不稳定，还没插入快
插入排序再样本小并且基本有序的时候效率很高；

希尔排序

希尔排序就是改进的插入排序

思想

先选一个间隔，比如为4，对上面的数每隔四个先进行插入排序，这样最后就变成最下面的那种；

然后缩小间隔，再来一遍，比如上面间隔为2的时候；
最后再进行普通的插入排序，就排完了；

因为如果比较小的数在后面，那么排序的时候需要移动的位置很远，复杂度很大，通过选择间隔，把小的数先移到前面，这样最后进行插入排序的时候就会很快；
间隔对时间复杂度有影响，如果间隔比较大，移动的次数少，移动的距离短。
但是因为是跳着排，因此不稳定。

代码

#include
#include
using namespace std;
class solution
{
     
public:
    void mysort(vector<int>& nums) 
    {
     
        int size = nums.size();
        for (int h = 4; h > 0; h /= 2) 
        {
     
            for (int i = h; i < size; i++)//从间隔的下一个开始
            {
     
                int j = i;
                while (nums[j - h] > nums[j] && j >= h)//
                {
     
                    swap(nums[j - h], nums[j]);
                    j = j - h;
                }
            }
        }
    }
};

测试就不写了，这里采用4为间隔可能不太合适，如果被排序的很长，那么其实并没有节省多少时间，因此可以把间隔设定为总长度的一半，然后不断除以二。这也是这个算法发明者最开始的想法

但是到后面人们发现这种除以二的间隔序列其实效率并不高，还有更好的间隔序列，我们讲解一下最常见的Knuth序列
h=1；
h=3*h+1；
程序可以这样写

#include
#include
using namespace std;
class solution
{
     
public:
    void mysort(vector<int>& nums) 
    {
     
        int size = nums.size();
        int h = 1;
        while (h <= size / 3) 
        {
     
            h = h * 3 + 1;
        }
        for (int gap = h; gap > 0; gap = (gap -1)/3)
        {
     
            for (int i = gap; i < size; i++)//从间隔的下一个开始
            {
     
                int j = i;
                while (nums[j - gap] > nums[j] && j >= gap)//
                {
     
                    swap(nums[j - gap], nums[j]);
                    j = j - gap;
                }
            }
        }
    }
};

除此之外还有以质数等方法；

分析

这种排序方法其实不怎么用，适合用于中型规模数据的排序；
空间复杂度为1，时间复杂度十分复杂， 采用不同的序列时间复杂度不一样，普遍的认为是n的1.3次方，不好计算，可以去看看数学；
一般而言就是上来一个快排……；

归并排序

思想

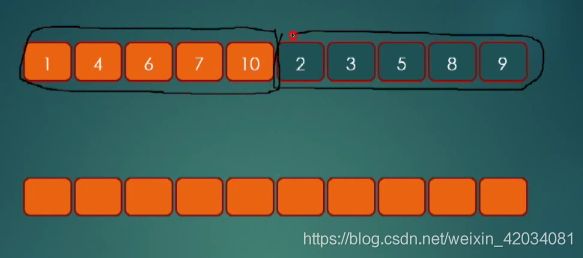
如果相对一整串数据进行排序，先把整串分成两半，看是否已经排好序，如果没有，再拆成两半，再看子数组的子数组是否排好序。直到字串排好为止
如果有排好，那么我们得到两个有序的数组，如上图所示。
我们先分配一块空间，我们用三个指针，分别指向新数组的首部，两个子数组的首部。
然后不断比较子数组的位置和新数组的首部指针，直到子数组全部塞入，然后更新原数组数据。
2个元素如果大小相等，没有外部干扰，将不会交换，因此是稳定的。

代码

#include
#include
using namespace std;
class solution
{
     
    //第二层递归
    void merge(vector<int>& nums,
        int left,//左边界位置
        int mid,//中间
        int right) //右边界位置下一个
    {
     
        vector<int> tempvec(right-left+1,0);
        int i, j, k;//三个指针
        i = 0;//表示新数组的首指针
        j = mid;//指在后半截数组的第一个位置上
        k = left;//指在前半截数组的第一个位置上；
        while (j <= right && k < mid)//当两个数组都没有遍历完
        {
     
            //把小的数挪到新数组上，
            //注意这里要写等号，因为我们要保证稳定性
            tempvec[i++] = nums[j] <= nums[k] ? nums[j++] : nums[k++];
        }
        //有可能其中一个数组遍历完了，另一个还没有遍历完
        while (j <= right)
        {
     
            tempvec[i++] = nums[j++];
        }
        while (k < mid)
        {
     
            tempvec[i++] = nums[k++];
        }
        //组合完直接修改之前的值，不然下次还是一样的。
        for (int m = 0; m < tempvec.size(); m++) 
        {
     
            nums[left + m] = tempvec[m];
        }
    }
    //第一层递归区间
    void assitant(vector<int>& nums, int left, int right) 
    {
     
        if (left==right) return;//结束条件
        int mid = left + (right - left) / 2;
        assitant(nums, left, mid);
        assitant(nums, mid + 1, right);
        merge(nums, left, mid + 1, right);
    }
public:
    void mysort(vector<int>& nums)
    {
     
        assitant(nums, 0, nums.size()-1);
    }
};

注意上面代码非常不建议使用右开区间，否则第一层递归函数非常不好写，不信各位试试看

分析

掰成两瓣的复杂度是log2n，每一个层交换的次数与n成正比，所以大概是nlog2n的时间复杂度；递归的时间复杂度不好算直接忽略，感兴趣可以去找找简单递归的复杂度计算方法；
空间复杂啊都就是n，因为复制了n个位置。
归并排序在实际应用中非常多，java和python对对象排序都是归并；

改进归并

TimSort，对数组进行分组，然后分组内部的元素进行二分插入排序，然后对所有组进行归并排序

快速排序

思想

首先找到一个基准，随便找，比如第一个数字，然后分成三部分，左边全放比基准小的，右边全选比基准大的，中间放跟基准相等的。
比如下面这张图，我们拿7当轴，进行分区；

排好之后，中间的7的位置就固定了

再拿3当轴和5当轴，这样就分到只剩一个，就可以拍好返回了。

值得注意的是，空间复杂度是logn，因此在分区的时候不允许构造完整的数组，因此常见的分区策略如下：

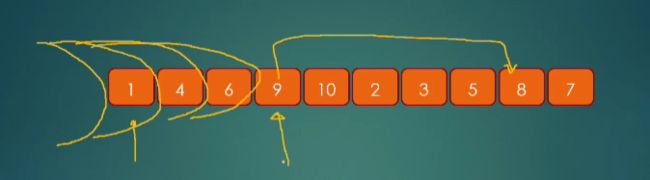
首先从左到右开始，如果数比轴小，则包含进入区内，如果比轴更大，那么我们将轴前面的数字和这个比轴更大数作交换，比如上面就是将146包含入内，9比7大，因此交换8和9的位置，再检查
比如此时我们交换完发现8比7还是要大，我们再进一步交换两个数的位置，也就是8和5，这个时候就可以把5扩进来；直到扩大的下一个位置和交换的点位置重合，那么我们就算分完了比7小的。
然后我们将轴移动到扩展区的后一个位置，那么我们就分区结束了。因为在小区的扩展同时，大区也在扩展。

快排中的分区策略：
经典快排采取更激进的策略，也就是两边同时找扩展区，然后做交换。比如这样

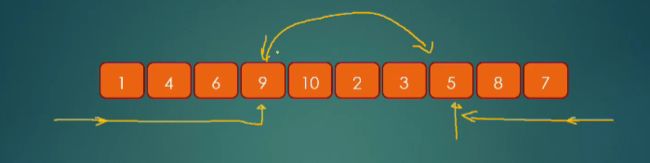
如上图所示，我们从左边找到第一个比轴大的数，从右边找到第一个比轴小的数，直接交换两数，省去了很多不必要的交换过程，这就是快排中的分区策略。

代码

#include
#include
using namespace std;
class solution
{
     
    
    int partition(vector<int>& nums,int left,int right) //右边界位置下一个
    {
     
        int pivot = nums[right];//定义轴
        int leftbound = left;
        int rightbound = right-1;//要减一，因为要避开轴
        while (leftbound <= rightbound)
        {
     
            //一直加到比分界值大
            while (leftbound <= rightbound &&nums[leftbound] >= pivot) {
      ++leftbound; }
            while (leftbound <= rightbound &&nums[rightbound] <pivot) {
      --rightbound; }
            if (leftbound < rightbound) swap(nums[leftbound], nums[rightbound]);

        }     
        //最后放轴的位置
        swap(nums[right], nums[leftbound]);
        return leftbound;//返回轴的位置；
    }
    void assitant(vector<int>& nums, int left, int right) 
    {
     
        if (left >= right) {
      return; }
        int mid=partition(nums, left, right);
        //对左边排序
        assitant(nums, left, mid - 1);
        //对右边排序
        assitant(nums, mid + 1, right);
    }
public:
    void mysort(vector<int>& nums)
    {
     
        assitant(nums, 0, nums.size()-1);
    }
};

有几个要注意的点：

1.因为有可能最后一个数是最大的数字或者最小的数字，因此while里面就会一直循环，
leftbound可能会变成负数，rightbound可能超过上线,因此要加入小于判断；
2.仅仅加入小于限制还是不够，因为对于最右边数字为最大数的情况，先进入内部第一个while循环，会一直循环到left=right-1,还不够，因为这样会造成最后哦交换轴位置的时候，会跟倒数第二个数交换，因此再加一个等号，这样对之前的比较并不会影响因为即使针对不是最大的数，后面的判断会限制，如果是最大数，就会多加一个，使最后的swap变成swap(nums[size - 1], nums[size - 1])；
3.第二个判断条件，只能有一边加等号，不然可能分解位置左右两边都有跟pivot相等的值
4.当输入的数字是2个的时候，根本没办法进入while，因此需要最外面一圈while需要加等号

分析

时间复杂度
每次是把数组分成两半，每次都是对数组 进行n/2次遍历，简化为n，长度为n时，需要进行log2n次的分片，因此时间复杂度为nlog2n的情况；
最好的情况也是这样；
最差的情况是当每次拿到的都是最值，那么第n个数都要跟前面比较n-1次，那么等差数列求和最差是n²
优化：
为了避免这种情况，可以事先进行判断是否用快排；
或者随机取一个数，而不是每次都取最后一个
空间复杂度
每分一次，就会创造常量级别的变量，因此空间复杂度是log2n；

改进双轴快排

双轴快排就是java内部的排序算法，双轴快排就是找两个数，把数组分成三个区域：

分成三个区，先把选出来的数从小到大排，这两个数分别成为小数和大数；
左边我们希望放比小数小的数；称为less区域
右边我们希望放比大数大的数；称为more区域
中间放小数和大数之间的数（包含两端）；称为mid区域
具体实现思路：
less区域放在最左边开始；
more从右边开始；
不断扩大less和more，如果处于哪个区间，就跟那个区间接壤的一个交换位置；
就是从两边不断吃掉中间的数字；
源码可以看java内部的DualPivotQuicksort类的sort成员函数
大规模的数组可以使用双轴快排，小量的直接插入排序，结构化好的（本身有一定规律的）使用归并排序，一般的就快排

最优查轴算法

首先算出数组长度的1/7；
找到数组中点，记录
中点加1/7，记录，再加1/7，记录
中点减1/7，记录，再减去1/7，记录
如果5个数都不想等，排序5个数，取第二个数和第四个为轴；再进行双轴快排
如果5个数有相等的情况，取第三个为轴，进行传统快排（单轴）；

计数快排

思想

其实计数排序是基于桶排序思想的一种排序；是一种非比较排序；适用比较特殊的范围：量大但是范围小

比如上面这张图，有很多个数，但是每个数都是整数而且范围十分有限，比如是统计公司1w人的员工年龄排序；
当我们读到一个数的时候，我们将下表对应的数加一，直到把所有数都读完为止；
然后我们从统计好的数组中，挨着从里面取数，比如有2个1，就写两个1，等等；

代码

随便写写，这代码是个人都会

#include
#include
#include
using namespace std;
class solution
{
     
public:
    void mysort(vector<int>& nums)
    {
     
        int minnum = *min_element(nums.begin(), nums.end());
        int maxnum = *max_element(nums.begin(), nums.end());
        vector<int> buket(maxnum-minnum+1,0);//记得加一
        for (auto it : nums) 
        {
     
            ++buket[it- minnum];
        }
        nums.clear();
        for (int i = 0; i < maxnum - minnum; i++)
        {
     
            while (buket[i])
            {
     
                nums.push_back(minnum + i);
                --buket[i];
            }
        }
    }
};

分析

空间复杂度为n+k，n为数组长度，k为桶的个数
时间复杂度，n+k，速度很快，但是空间复杂度大；
缺点
这种算法不能对对象进行排序，比如一个object，里面有age，id，性别等信息，我们希望根据age排序，会丢掉其他的信息，因此不能这样写，这样写的东西不稳定，同一个东西放进去分不清楚谁是谁了，也就是不稳定

稳定计数排序算法

加一个累加数组，记录没一个数组在排好序的数组中最后一个数字下标的位置比如说
0 0 0 1 1 2 2 2 2；
那么三个桶数分别为 3 2 4；
累加数组就是 3，3+2，3+2+4；
然后我们从尾到头遍历数组，遍历到第一个1，比如说，我们就把1放到下标为3+2-1也就是新数组的第4个位置，然后累加数组减一，下次碰到1，就放到第3个位置，这样就是稳定的，相对位置不会改变，就能对对象进行排序了。

基数排序

思想

本质上是一种多关键字的排序，根据不同的权重的对对象不同的特征进行排序

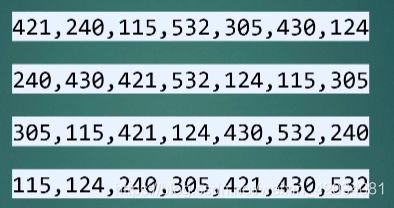
假如我们有这样一个数组，我们先对所有数字的个位数进行排序，把个位数小的放前面，一样的放在一起；然后输出
再对排好的十位数进行同样操作
最后对百位数进行同样操作
位数按照最高位为准，不够就认为是0；

代码

#include
#include
#include
using namespace std;
class solution
{
     
public:
    void mysort(vector<int>& nums)
    {
     
		//求最高位数
        int count = 0;
        for (auto it : nums) 
        {
     
            int temp = it;
            int counttemp = 0;
            while (it > 0) 
            {
     
                it = it / 10;
                ++counttemp;
            }
            count = max(count, counttemp);
        }
        assitant(nums, count);
    }
    void assitant(vector<int>& nums, const int count) 
    {
     
        int size = nums.size();
        vector<int> result(size, 0);
        vector<int> buket(10, 0);
        for (int i = 0; i < count; i++) 
        {
     
            int division = static_cast<int>(pow(10, i));
            for (int j = 0; i < size; j++) 
            {
     
                //这一步很关键，是求每一位的数是多少，
                int num = nums[j] / division % 10;
                ++buket[num];//放入桶中
            }
            //求累加数组，保证稳定
            for (int m = 1; m < buket.size(); m++)
            {
     
                buket[m] = buket[m] + buket[m - 1];
            }
            //
            for (int n = size - 1; n >= 0; n--) 
            {
     
                int num = nums[n] / division % 10;
                //累加是从1开始算的，因此前减减
                result[--buket[num]] = nums[n];
            }
        }
        nums = result;
    }
};

分析

空间复杂度，n，同样大小额外空间就能满足要求
时间复杂度，nk，看复制几遍
本质上每一次循环都是一次计数排序，是一种关键字排序；
有低位优先和高位优先进行排序；
上面写的是稳定版本；
高位的话先分大桶再在大桶里面放小桶，一种递归和分治的思想
空间复杂度高，这里已经尽量降低空间复杂度了，一般你百度出来的都是n方空间复杂度；
也可以用于字符串的排序

桶排序

思想

桶排序其实更普通意义上的桶排序，不只是指基数和计数；

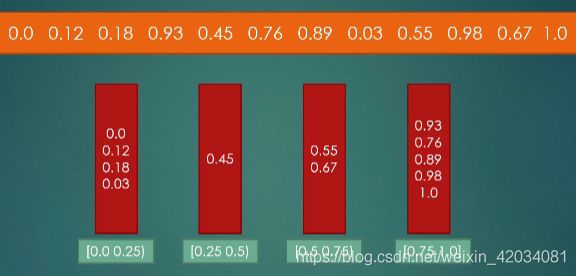
这里我们拿给小数排序的例子来看，当然你也可以换成整数排序；
比如上面的12个小数，我们可以对0-1分成4个桶，当然你也可以分成5个10个桶；
遍历每一个元素，看它属于哪一个桶，放进去；
桶里面进行单独的排序，
最后从左到右进行输出；

分析

因为这种方法太一般性了， 因此没有标准的代码，上面的两种都算是桶排序；
这里面有很多值得探讨的空间，比如每个桶内部的存放方式，
如果是数组存储
是不是应该每个桶分配跟原数组一样的长度，因为我们要考虑到极端情况；
如果改为动态数组，那么不可避免要经历扩容和搬移的过程，又会损耗效率
如果是链表
链表确实空间复杂度小了，但是对链表的排序非常复杂，本质上是一个冒牌排序，复杂度是n平方，时间复杂度又高了。
一般做法
是动态数组，内部用归并、快排。
时间复杂度
每个内部是归并或者快排，我们有k个桶，那么每个桶就是n/k*log(n/k)；
一共k个桶就是nlog(n/k)；这个值跟遍历的复杂度比起来很小，因此一般认为复杂度就是n+k；
但是其实因为这个方法常数项非常大，因此其实效率不见得有nlogn高；
最极端就是都装一个桶里面，复杂度是n平方，最好的就是n（一个桶里一个）
空间复杂度
最好是n，链表，动态数组
最坏是n平方，每个桶装size个；

堆排序

在讲堆排序之前需要各位知道什么是二叉树，这里就不扯了；

什么是堆

堆结构比堆排序重要得多，各位可以不吃饭不睡觉但是不能忘记堆结构
结构
堆结构上是一个完全二叉树；完全二叉树不同于满二叉树，可以有空的，但是只能在最后面，而且最后一层必须是从最多端开始连续不断；
但是它在实际存放的数据大小上有讲究，我们又将其分为大根堆和小根堆
大根堆就是每一棵子树最大值都是头节点的值；
小根堆的每一棵子树最小值都是头节点的值；
表示
当然了我们可以用二叉树表示堆，我们也可以用数组表示堆；
如何用数组表示堆
比如我们有一个数组，size100；
我们把0看作是根节点，1看作是左子树的根节点，2看作是右子树根节点，3看作1的左子树根节点，4看作1右子树根节点……依次类推，我们就可以利用数组表示二叉树；
这些下标隐含这些关系：
根节点下标为i，那么其左子树根节点下标为2i+1；右边为2i+2；其父为(i-1)/2，取整；因此我们可以根据任何一个节点找到其父节点脚标，左右子树根节点；

当我们频繁要算一个坐标的左孩子，位运算速度大于乘法，因此有些时候人们不用0当作根节点；而用1；
这样一来就隐含这些关系：
根节点下标为i，那么其左子树根节点下标为i<<1；右边为i<<1|1；其父为i>>1，这样算起来很快；
这里我们还是用从0开始；不用什么骚操作

代码

对于一个大根堆
当插入一个值的时候，我们用以下代码简单实现

       vector<int>heap(100);
       int index = heap.size();
       heap.push_back(inputnum);
       while (heap[index] > heap[(index - 1) / 2]) 
       {
     
           swap(heap[index], heap[(index - 1) / 2]);
           index = (index - 1) / 2;
       }

也就是不断往上看或者来到0，自动退出，因为自己不会大于自己；
当删除一个数的时候，如果我们分析最极端情况，我们想删除最大的数，但是剩下的仍然保持大根堆；
我们可以通过以下代码简单实现

#include
#include
#include
using namespace std;
class solution
{
     
public:
    void deletop(vector<int>& nums)
    {
     
        vector<int>heap(100);
        heap[0] = heap[heap.size() - 1];
        heap.erase(heap.end() - 1);
        heapify(heap, 0, heap.size() - 1);
    }
    void heapify(vector<int>& nums, int index, int size) 
    {
     
        int left = index * 2 + 1;
        while (left < size) //当我至少有左孩子的时候
        {
     
            //largest表示孩子最大值
            int largest = left;
            //当你有右孩子并且值比左孩子大的时候
            //右孩子胜出
            if (left + 1 < size && nums[left + 1] > nums[left]) 
            {
     
                largest = left + 1;
            }
            //如果孩子中最大的比自己小，那么直接退出
            if (nums[largest] <= nums[index]) 
            {
     
                break;
            }
            else//否则 
            {
     
                //交换位置
                swap(nums[index], nums[largest]);
                //更新index和left;
                index = largest;
                left = index * 2 + 1;
            }
        }
    }
};

有了上面插入和删除操作，我们就可以实现堆排序

#include
#include
#include
using namespace std;
class solution
{
     
public:
    void mysort(vector<int>& nums)
    {
     
        vector<int>output;
        vector<int>heap;
        for (auto inputnum: nums)
        {
     
            int index = heap.size();
            heap.push_back(inputnum);
            while (heap[index] > heap[(index - 1) / 2])
            {
     
                swap(heap[index], heap[(index - 1) / 2]);
                index = (index - 1) / 2;
            }
        }

        while (!heap.empty()) 
        {
     
            output.push_back(heap[0]);
            heap[0] = heap[heap.size()-1];
            heap.erase(heap.end() - 1);
            heapify(heap, 0, heap.size());//使对象变成堆
        }
        nums = output;
    }
    void heapify(vector<int>& nums, int index, int size) 
    {
     
        int left = index * 2 + 1;
        while (left < size) //当我至少有左孩子的时候
        {
     
            //largest表示孩子最大值
            int largest = left;
            //当你有右孩子并且值比左孩子大的时候
            //右孩子胜出
            if (left + 1 < size && nums[left + 1] > nums[left]) 
            {
     
                largest = left + 1;
            }
            //如果孩子中最大的比自己小，那么直接退出
            if (nums[largest] <= nums[index]) 
            {
     
                break;
            }
            else//否则 
            {
     
                //交换位置
                swap(nums[index], nums[largest]);
                //更新index和left;
                index = largest;
                left = index * 2 + 1;
            }
        }
    }
};

当然了，我们也可以借助c++本身自带的堆容器，代码更加简洁，如下：

#include
#include
#include
using namespace std;
class solution
{
     
public:
    void mysort(vector<int>& nums)
    {
     
        make_heap(nums.begin(), nums.end(), greater<int>());
        sort_heap(nums.begin(), nums.end(), greater<int>());
    }
};

分析

时间复杂度
如果有n个数，那么其实总共的层数是log2n级别，每插入一个新的数字 ，它的位置调整只跟自己的父节点有关系，也就是层数，因此每一步不管是插入还是删除都是log2n的级别；
因此n个数就是nlog2n的复杂度
空间复杂度
上面其实写的空间复杂度有点高，是n，如何变成1呢？

优化
有一种方法可以使得插入为n复杂度，也就是说n就可以成为大根堆；
我们可以直接把这堆数想象成二叉树；从最后一个向前遍历，如果发现父节点数比自己小就交换，直到循环完，这样时间复杂度就是n
我们发现其实上述过程就是heapfy的过程，只不过从右往左的，因此我们可以这样改进

        for (int i = nums.size() - 1; i >= 0; i--) 
        {
     
            heapify(nums, i, nums.size());
        }

如果我们忽略输出的output数组来保存，也就是直接输出不缓存，那么确实它的空间复杂度就变成了1；